基于Hausdorff距离的曲线降阶算法

陈小雕，王 辉，郑金生

(杭州电子科技大学计算机学院，浙江 杭州，310018)

0 引言

曲线曲面的降阶逼近问题在CAD/CAM中有着很重要的应用。实际的工程应用中，高次的参数曲线或曲面经常在使用前被要求转化到更低次数的曲线或曲面。曲线曲面的降阶算法也可以被应用到数据压缩中。对于Bézier曲线曲面来说，相应的降阶逼近算法就是重新计算用于逼近的Bézier曲线曲面对应的控制点。很多文献讨论了曲线曲面的降阶逼近问题［1－10］。大部分方法是寻求某个目标距离函数的最优或次优的解。第一类方法是最小化给定曲线和逼近曲线间的最大欧氏距离。这类方法主要借助Chebyshev多项式来寻求无穷范数下最优的解［4，5］。第二类方法是寻求L2范数下的最优解，Legendre多项式方法，Jacobi多项式方法和对偶Bernstein基等等，被用来求解L2范数下的最优解。这些方法给出了对应控制点的显式表达式，甚至相应的误差估计。此外，还有圆盘Bézier曲线(对应控制点是圆盘表示的Bézier曲线)的降阶问题，B样条曲线的降阶问题。最近，又提出了基于重新参数化的降阶思想，在具体的算法实现中，函数很难解析表示或表达式过于复杂。本文尝试使用分段二次函数来替代函数。与函数t相比，H(t)可以更好地逼近函数，相应的算例也表明了新算法的逼近效果。

1 基于分段二次函数重新参数化的算法

基于Hausdorff距离是以Hausdorff距离最小化为目标，在曲线研究中，Hausdorff距离是衡量两条曲线逼近程度的重要标准。本文正是这个基础上提出了基于分段二次函数从新参数化的算法。该算法的具体实现过程如下:

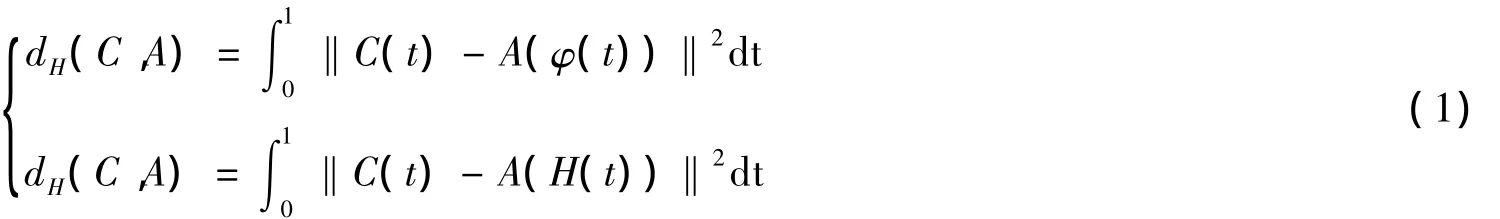
最小化函数dH(C，A)可以减少C(t)－A(H(t))‖2的值，且这个值通常等同于给定曲线H(t)和逼近曲线A(t)间的Hausdorff距离，这个重新参数化的算法可以取得Hausdorff距离下更好的逼近效果。

在给定曲线C(t)上选定若干点，参数设为0=t0＜t1＜…＜tk＜tk+1=1，设Hi(t)=ait2+bit+ci满足:

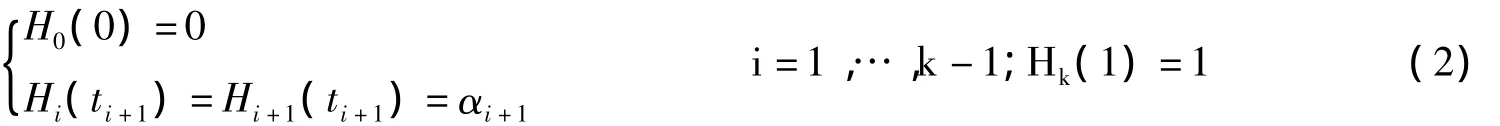
式中，0=α0＜α1＜…＜αk＜αk+1=1，共有k+1个关于c0，…，ck的线性方程，可以求解得到:

关于控制点坐标 xij的二次项。记 V=［a0，b0，…，ak，bk］T=［v1，…，v2k+2］T。若 V 确定，则结合式 3得知ai、bi、ci也固定，最小化dH(C，A)等价于求解一个线性方程组，可以相应地得到:

将式5代入式4中，得到dH(C，A)=f(v1，…，v2k+2)最小化f(v1，…，v2k+2)等价于求解:

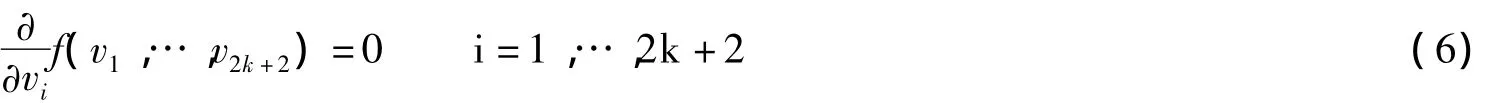
求解式6，得到待定参数v1，…，v2k+2的值。再代入式5中，得到最终控制点对应的坐标xi，j。为简化计算量，可用最小化函数f(v1，…，v2k+2)在点V0=(0，1，…，0，1)T处的二次泰勒展开式:

然后求解得到函数最小值以及对应参数的值，代入式7中，得到最终控制点对应的坐标。

2 实例与讨论

例1 如图1所示，实心线为给定的11次Bézier曲线，相应控制点为(114，41)、(107，237)、(86，－131)、(90，－71)、(179，320)、(200，291)、(117，2)、(104，－118)、(119，34)、(184，324)、(171，127)和(192，24)。虚折线是利用L2范数方法得到的逼近曲线，对应的Hausdorff距离为8.404。虚点线是本文算法采用一段二次曲线逼近的结果，对应的Hausdorff距离为4.796。当分段点在原始曲线上的参数为i/10，i=1，…，9时，相应的逼近曲线对应的Hausdorff距离均为4.796。图1(b)是对应的误差曲线。

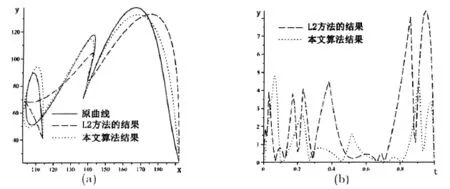
图1 Bézier曲线从11次降到6次

例2 如图2所示，红色的实心线为给定的7次Bézier曲线，相应控制点为(30，－10)，(40，20)，(45，20)，(55，15)，(65，0)，(70，－10)，(80，10)和(100，－5)。黑色的虚折线是利用 L2范数方法得到的逼近曲线，对应的Hausdorff距离为1.347。蓝色的虚点线是本文算法采用一段二次曲线逼近的结果，分段点的参数简单的设置为1/2，对应的Hausdorff距离为0.213。图2(b)是对应的误差曲线。

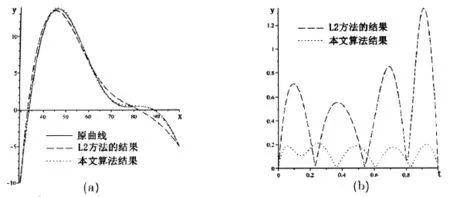
图2 Bézier曲线从7次降到4次

例3 如图3所示，红色的实心线为给定的10次Bézier曲线，相应控制点为(30，－10)，(40，20)，(45，20)，(55，15)，(65，0)，(70，－10)，(80，－30)，(95，10)，(105，20)，(90，50)和(70，20)。黑色的虚折线是利用L2范数方法得到的逼近曲线，对应的Hausdorff距离为3.492。蓝色的虚点线是本文算法采用一段二次曲线逼近的结果，分段点的参数简单的设置为1/2，对应的Hausdorff距离为0.830。图3(b)是对应的误差曲线。

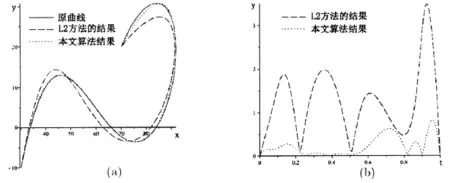
图3 Bézier曲线从7次降到4次

随着用于逼近的曲线次数和分段函数H(t)分段点的增加时，本文算法用于确定H(t)的计算量增加很快;另一方面，L2范数方法的逼近效果本身也比较不错，本文新算法改进的幅度相对来说比较有限。这种情况下，对于那些时间要求较高的应用领域，建议直接采用L2范数方法。

3 结束语

本文采用Hausdorff距离衡量逼近曲线和原始曲线的误差，并基于Hausdorff距离提出了重新参数化的思路，用于求解Bézier曲线的降阶逼近问题。具体实现中，本文采用分段二次函数H(t)来近似式1中函数φ(t)。当函数H(t)确定时，求解逼近曲线控制点的计算量和L2范数方法相应的计算量相当。例子也表明了在Hausdorff距离下新算法可以具有更好的逼近效果。当逼近曲线的次数较高和分段函数H(t)的分段点较多时，用优化方法来确定H(t)的计算量较大。如何直接根据曲线的形状来快速估算H(t)的分段点以及相应的表示，将是今后的工作之一。本文算法的思路，理论上也可以推广到B样条曲线或曲面的降价逼近问题中。这种类似的推广，以及Hausdorff距离的快速估算，将是今后的另一个工作方向。

［1］Ahn Y.Degree reduction of Bézier curves with Ck-continuity using Jacobi polynomials［J］.Computer Aided Geometric Design，2003，20(8):423–434.

［2］Bogacki P，Weinstein S E，Xu Y.Degree reduction of Bézier curves by uniform approximation with endpoint interpolation［J］.Computer-Aided Design，1995，27(9):651–661.

［3］Brunnett G，Schreiber T，Braun J.The geometry of optimal degree reduction of Bézier curves［J］.Computer Aided Geometric Design，1996，13(8):773–788.

［4］Lachance M A.Chebyshev economization for parametric surfaces［J］.Computer Aided Geometric Design，1988，5195－208.

［5］Eck M.Least squares degree reduction of Bézier curves［J］.Computer-Aided Design，1995，27(11):845 －851.

［6］Ahn Y，Lee B，Park Y.Constrained polynomial degree reduction in the L2－norm equals best weighted Euclidean approximation of Bézier coefficients［J］.Computer Aided Geometric Design，2004，21(2):181 －191.

［7］Lu L Wang.G Application of Chebyshev II－ Bernstein basis transformations to degree reduction of Bézier curves［J］.Journal of Computational and Applied Mathematics，2008，21(1):52 －65.

［8］Lu L.A note on constrained degree reduction of polynomials in Bernstein－Bézier forms over simplex domain［J］.Journal of Computational and Applied Mathematics，2009，29(1):324－326.

［9］Zhang R Wang.G Constrained Bézier curves'best multi－degree reduction in the L2 －norm［J］.Progress in Natural Science，2005，15(9):843－850.

［10］Zhou L，Wang G.Constrained multi－degree reduction of Bézier surfaces using Jacobi polynomials［J］.Computer Aided Geometric Design，2009，26(3):259－270.