不确定广义双线性系统的鲁棒无源控制
2012-09-28张秀华张庆灵
张秀华,张庆灵
(东北大学理学院,辽宁沈阳 110819)
不确定广义双线性系统的鲁棒无源控制
张秀华,张庆灵
(东北大学理学院,辽宁沈阳 110819)
研究了不确定广义双线性系统的无源控制问题.利用广义李雅普诺夫函数、广义黎卡提代数不等式和线性矩阵不等式,给出了不确定广义双线性系统的零解渐近稳定和无源的充分条件.特别针对广义双线性系统,采取了范数有界和集合限定的方法,设计了状态反馈控制器,使得闭环系统是零解渐近稳定且具有无源性,同时给出了相应的控制器的构造.最后,给出了一个实例说明所得结论的正确性.
不确定;双线性;广义;无源;鲁棒
广义系统是一种多级、多目标、多维数和多层次的大规模的复杂系统,而广义双线性系统是一种介于广义线性系统与广义非线性系统之间的系统,可以看成一类特殊的广义非线性系统,是研究其他广义非线性系统的基础.广义双线性系统解的存在性以及稳定性研究虽然已经取得了一定的成果[1-4],但仍有必要进行深入的探讨.
耗散性理论在系统稳定性研究中起着重要的作用.而无源性是耗散性的一个重要方面,它将输入输出的乘积作为能量的供给率,体现了系统在有界输入条件下能量的衰减特性.事实上,基于李雅普诺夫函数的镇定理论,也可从无源性的角度加以解释.可以说,无源性是稳定性的一种更高层次的抽象,近年来已经引起了一定的关注[5-8].
在实际问题中,常常不可避免地受到不确定因素的影响.不确定因素经常导致许多物理过程性能的不稳定性.本文将广义系统和介于线性与非线性系统之间的双线性系统结合起来,进一步开展一类不确定广义双线性系统的无源性研究,在理论上和实际应用中都是很有意义的.
1 问题描述与预备知识
考虑如下一类不确定广义双线性系统:
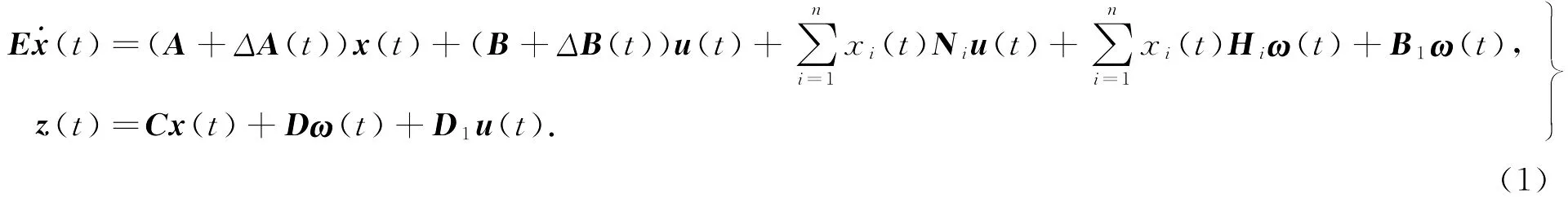
式中,x(t)∈Rn是状态变量,u(t)∈Rm是输入控制,ω(t)∈Rp是外部输入,z(t)∈Rn是输出变量;Ni∈Rn×m,Hi∈Rn×p(i=1,2,…,n)是常数矩阵;E,A,B,B1,C,D,D1是适当维数的已知常数矩阵,其中,r a n kE=r<n;ΔA(t),ΔB(t)是时变不确定实矩阵函数.考虑的不确定性假定是范数有界的,且具有如下形式:

式中,M,Na,Nb是具有适当维数的实常数矩阵;F(t)∈Ri×j是一个具有Lebesgue可测元的时变不确定矩阵函数,满足
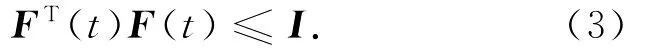
满足上述条件的ΔA(t),ΔB(t)称为是允许的.
为给出描述系统的稳定与无源控制的有关结论,先考虑具有如下形式的不确定广义双线性系统:

记系统(4)的标称系统为
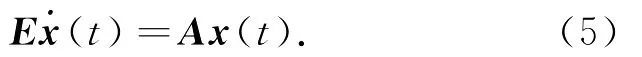
引理1[9]系统(5)容许的充要条件是Lyapunov方程

对任意的W>0,有满足rank(ETP E)=rankP=r的唯一半正定解P.
本文中,始终假定系统(5)是容许的.
引理2[10]给定具有适当维数的矩阵Q,H,M,其中,Q对称,则
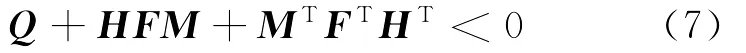
对所有满足FTF≤I的F成立,当且仅当存在一个常数ε>0,满足
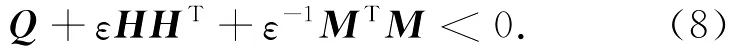
定义对于系统(4),如果存在非负连续可微函数V(x(t)),V(0)=0,使得不等式

对一切输入ω(t)和所有允许的不确定性均成立,则称系统(4)是无源的.
引理3[11]对于任意的n维向量x,y,有2xTy≤γ xTx+γ-1yTy,∀γ∈R+.
2 无源性分析
定理1对于系统(4),若存在正实数α和正定矩阵W1,满足
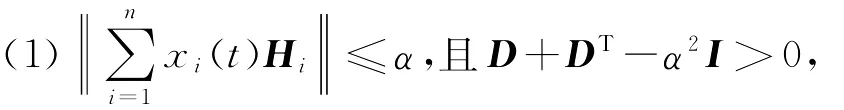
(2)对于满足方程(6)的正定矩阵W及半正定矩阵P,有

则系统(4)是零解渐近稳定且无源的.
证明 取系统(4)的Lyapunov函数为
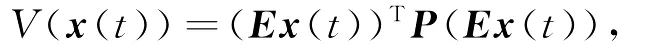
则V(x(t))沿系统(4)的导数为
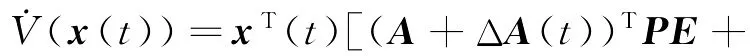

由引理3,有
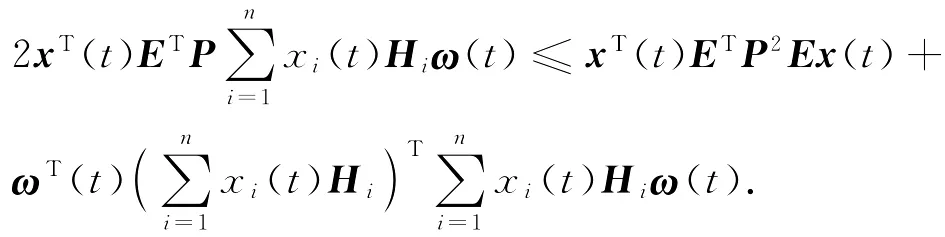
由引理3及式(2)和式(3),有
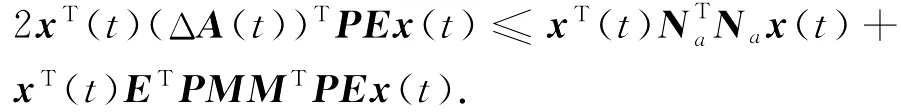
结合式(6),所以

先考虑系统(4)的零解渐近稳定性.令ω(t)=0,当式(10)成立时,显然有
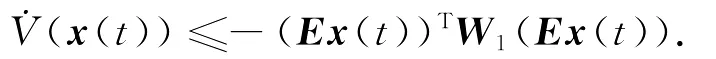
再考虑系统(4)的无源性.计算可得

当定理中条件成立时,由Schur补性质知
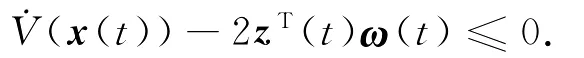
3 无源控制
假设存在如下线性状态反馈控制律:

式中,K为常数增益矩阵.
于是,从式(1)和式(11)得到闭环系统的状态方程为

式中,ut∈R是控制向量;BD1是适当维数的常数矩阵.下面讨论系统(12)的零解渐近稳定且无源问题.
定理2对于系统(1),如果D1列满秩,且存在正实数α,β和正定矩阵W1,W2,满足

(2)记集合

Rn,对于满足方程(6)的正定矩阵W及半正定矩阵P,满足如下式子:
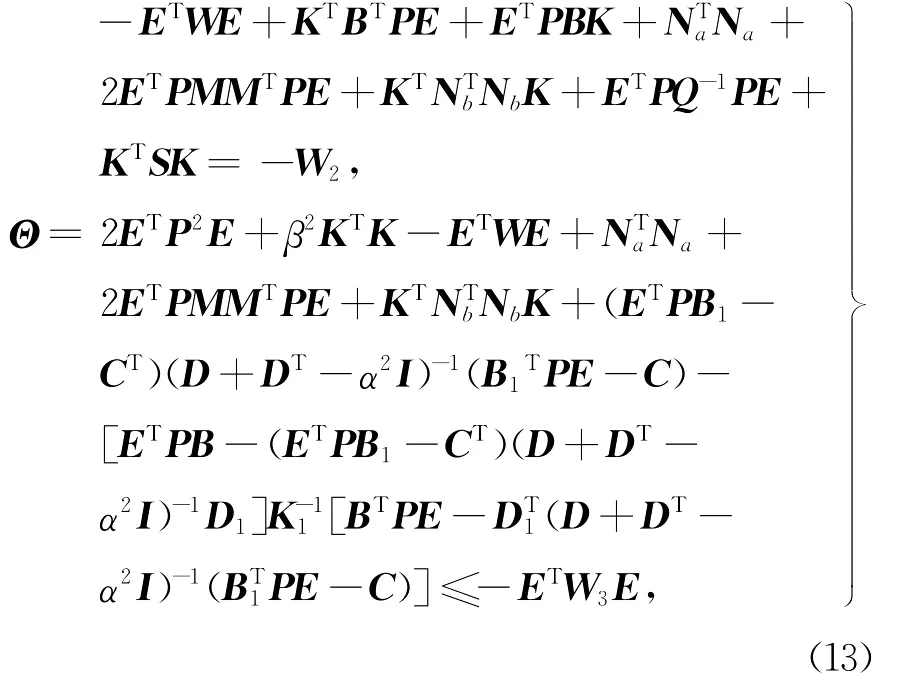
式中,S和Q为正定矩阵,K1=DT1(D+DT-α2I)-1D1,则存在状态反馈控制K,使得闭环系统(1 2)是零解渐近稳定且无源的,而且控制器可设计为
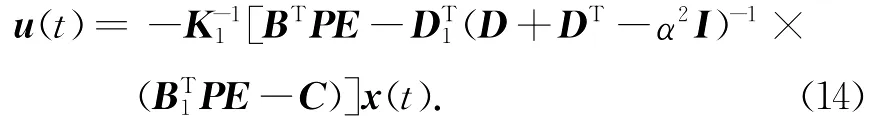
证明 取V(x(t))同前,先考虑系统(12)的零解渐近稳定性.令ω(t)=0,则有

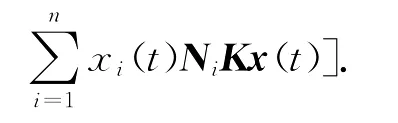
注意到式(2)和式(3),由引理1和引理3,可以得到
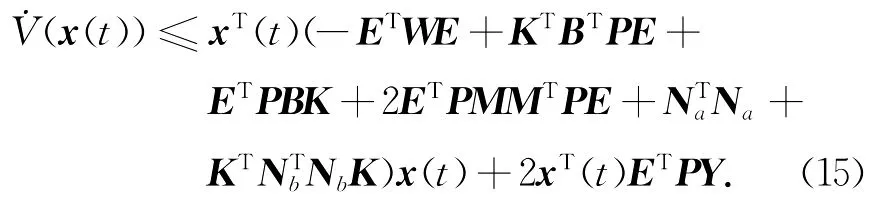
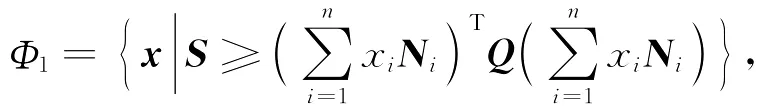
其中,S和Q为正定对称矩阵.对于任意的x∈Φ1,有

于是,可以将式(15)改写成如下形式:

此时只要

则对于x≠0,x∈Φ1,就有

所以,根据Lyapunov判别法,闭环系统(12)是零解局部渐近稳定的.
再考虑系统(12)的无源性.计算可得
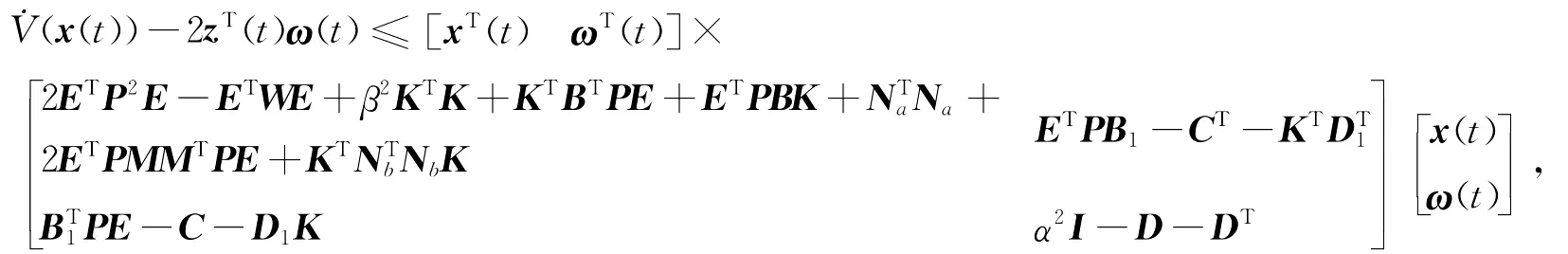
只要上式右端的矩阵小于或等于零即可.当D+DT-α2I>0时,上式等价于

将式(18)左端整理后即为

进一步地,可以考虑系统(1中系数矩阵均带有不确定项的情况,利用引理2和引理3,可以得到类似于定理2的结果.
4 数值算例
例 考虑系统(4),其中

由Matlab工具计算得到

满足方程(4),而且条件(1)、(2)及式(1 0)成立,由定理1知系统(4)无源且零解渐近稳定.
5 结 语
本文对不确定广义双线性系统的无源控制问题进行了研究.将无源性概念引入到不确定双线性广义系统,利用Lyapunov函数和线性矩阵不等式进行了无源性分析,给出了系统零解渐近稳定和无源的充分条件.在此基础上,特别针对广义双线性系统的非线性项,采取了范数有界和集合限定的方法,此处的双线性项处理,不是直接看成非线性项进行的范数有界约定,而是结合双线性项本身的特点,进行了巧妙的范数有界约定.同时对不确定项也进行了一定的处理,设计了静态状态反馈控制器,使得闭环系统是零解渐近稳定且具有无源性.给出了相应的控制器的构造.
[1]Lewis F L,Mertzios B G,Marszalek W.Analysis of singular bilinear using walsh functions[J].IEEE Proceedings-D,1991,138(2):89-92.
[2]张秀华,张庆灵.双线性广义系统稳定性控制分析[J].系统工程学报,2006,21(2):192-195.
[3]Zasadzinski M,Magarotto E,Rafaralahy H,et al.Residual generator design for singular bilinear systems subjected to unmeasurable disturbances:an LMI approach[J].Automatica,2003(39):703-713.
[4]兰奇逊,梁家荣.不确定广义双线性系统的鲁棒镇定问题[J].自动化学报,2008,34(6):707-710.
[5]Byrnes C J,Isidori A,Willems J C.Passivity,Feedback Equivalence and the Global Stabilization of Minimum Phase Nonlinear Systems[J].IEEE Trans.Automat.Contr.,1991,36(11):1228-1240.
[6]Li Z H,Wang J C,Shao H H.Delay-dependent dissipative control for linear time-delay systems[J].Journal of the Franklin Institute,2002,339:529-542.
[7]董心壮,张庆灵.时变不确定广义系统的鲁棒无源控制[J].控制理论与应用,2004,21(4):517-520.
[8]俞立,潘海天.具有时变不确定线性系统的鲁棒无源控制[J].自动化学报,1998,24(3):368-372.
[9]张庆灵.广义系统结构稳定判别的李亚普诺夫方法[J].系统科学与数学,1994,14(2):117-120.
[10]Xie L H.Output feedback H∞control of systems with parameter uncertainty[J].Int.J.Control,1996,63(4):741-751.
[11]Jin H,Bien Z G.Robust stability of uncertain linear system saturating actuators[J].IEEE Trans.Automat.Contr.,1994,39(1):202-206.
Robust Passive Control for Uncertain Singular Bilinear System
ZHANG Xiuhua,ZHANG Qingling
(School of Science,Northeastern University,Shenyang 110819,China)
The robust passive control problem for a class of uncertain singular bilinear systems is investigated.By means of generalized Lyapunov function and generalized Riccati inequality and linear matrix inequality,a sufficient condition is derived such that a prescribed uncertain singular bilinear system is passive and its zero solution is asymptotically stable.By making use of the method of norm bounded and limited collection,a state feedback control law is designed such that the closed-loop system is passive and its zero solution is asymptotically stable.Finally,an example is given to illustrate the validity of the obtained results.
uncertainty;bilinear;singular;passive;robust
TP13
A
1008-9225(2012)04-0041-04
【责任编辑:李 艳】
2012-02-29
国家自然科学基金资助项目(60974004).
张秀华(1963-),女,辽宁铁岭人,东北大学教授,博士.
