基于超级运输网络模型的综合运输政策效果分析

石海平，陆 婧，杨忠振

（大连海事大学 交通运输管理学院，辽宁 大连 116023）

1 背景

超级运输网络是指由多种运输方式构成的运输网络，依据超级运输网络组织综合运输可以充分发挥各种运输方式的优势，获得最佳的运输效果。其中，最具有代表性的是集装箱多式联运。因为它以集装箱为运输单元,将不同的运输方式有机地组合在一起,构成一体化运输，通过单次的托运，计费，单证，保险，由各运输区段的承运人共同完成货物的整体运输[1]。这种方式以集装箱为媒介,把海路、铁路、公路、内河水路等多种运输方式有机地结合,衔接为一体。

确定多式联运的整体方案时，需要知道各种运输方式的费用、所需的时间以及可靠性。因此，需要在超级网络上分析两点之间的最短路径、分析这些最短路径的方式构成、货物在不同运输方式间转换时发生的费用和时间等。因此在优化综合运输方案时，必须在网络上进行量化分析，所以需要建立一个计算机识别的超级运输网络模型。

近年来有很多关于综合运输的研究，但是，国内的研究多以定性描述和比较分析为主，构建量化分析模型的研究很少。例如，有关集装箱多式联运的研究都比较宏观，研究方法多采用定性描述，许多研究指出了综合运输中存在的问题，提出了改善措施。定量研究主要集中在码头或枢纽选址方面，例如郭子坚等的研究[2]。另外，王涛和王刚[3]在分析各种运输方式的特征后，构建了一个超级运输网络，但是其网络结构过于复杂。魏航等[4]在计算最短路径时考虑了时变网络所导致的时间、费用和风险的变化，但是，模型和算法比较复杂，且忽略了枢纽的换装能力。张建勇和郭耀煌[5]提供了一种构建超级运输网络和交通量分配的想法，但是没有进行算法设计和定量计算。

国内的大多数研究没有采用网络分析的方法计算改善措施的效果，以及这些措施对多式联运的敏感程度。大部分利用数学模型进行综合运输政策分析的研究出现在国外，例如，Nijkamp(2004)[6]利用Logit/Probit离散选择模型和神经元网络模型，比较优化模型和预测模型对超级运输网络上的物流优化和预测的能力。Beuthe[7]研究铁路、公路、水运三种运输方式的直接和交叉的需求弹力系数，利用超级运输网络计算了巴尔干地区10种不同货类的运输费用。他开发的交通需求分配模型全面考虑了整个网络的特征。Southworth(2000)[8]应用单一的数字表现形式表达超级运输和跨州际的货运网络。研究了运输系统和物流系统对环境的影响，以及从运输的角度控制和防止污染的方案等。Kozan[9]开发了一个网络模型来分析系统中集装箱的运输过程，其模型可以被看作是一个投资多式联运集装箱枢纽港的决策支持系统。

目前，对于超级运输网络的研究多集中在网络的最短路的算法上，而对于网络模型的建立、转运枢纽与转运链接在网络模型表现形式研究较少，这些给分析综合运输方案和政策带来了困难。本文在各种运输网络的特征、结构以及用户在起终点间的路径选择行为的基础上，提出构建超级运输网络模型方法，针对网络模型中虚拟链接的涵义给出三种虚拟链接的建立方法，它们分别是基于属性的虚链接建立、基于城市道路子网络模型的虚链接建立以及基于多尺度表达的虚链接建立。最后根据三种虚联接的表现方法，以三种方式构建中国东北地区的超级运输网络模型，然后比较三种网络模型的效用，并利用高效的网络模型分析一系列综合运输政策。

2 超级运输网络模型

2.1 超级运输网络模型的概念

超级运输网络包含公路网、铁路网、内河／远洋航线网、空中航线网等多种运输子网络，它把不同的运输方式有机地结合起来。超级运输网络模型中有代表铁路、公路或水路通道的实链接，还要有代表两种运输方式间衔接关系的虚链接。实链接具有通行时间、通行费用、通行能力等属性，虚链接具有转运所需费用、转运所需时间等属性。实链接表示实际存在的运输通道。虚链接的运输阻抗可以体现各方式之间的衔接效果，例如，港口建设表现为与该港口相关的实链接之间衔接的改善。因此，虚链接结构的难易程度对网络模型的复杂程度影响大，如果虚链接结构复杂，网络模型的难度会增加；但虚链接结构过于简单，则难以准确反映两种运输方式间的转运关系。图1是一个简单的超级运输网络模型，它包含公路子网络、铁路子网络、虚链接以及转运枢纽。建立超级交通网络模型的主要工作就是研究虚链接的表现和制作方法，下面以公路子网络和铁路子网络为例来予以研究。

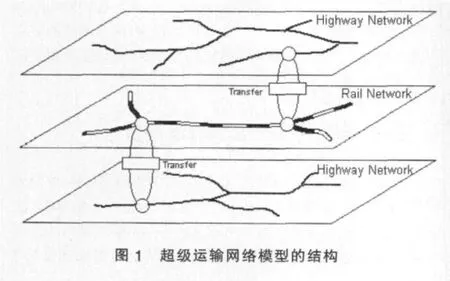
2.2 基于属性的虚链接制作方法

由于公路子网络和铁路子网络处于不同的网络中，因此超级运输网络模型需要利用虚链接将它们连接起来。图2是基于属性的虚链接的制作方法，该方法把货物在两个子网络间转运时产生的耗时、费用、可靠性等事件记录为虚链接的属性。

如果一个节点衔接宏观上铁路和公路网络，其不一定是同一个地点，而可能是同一个城市的两个枢纽，因此需要利用两枢纽间的公路和铁路枢纽间来转运货物。例如，集装箱经由高速公路运抵城市A后再利用铁路进行下一程的运输时，要经A市的城市道路将集装箱运送到铁路货站，然后在货站内编组后开始铁路运输。因此这种虚链接的属性就是在城市道路网上两点间路径的属性。由于很难结合城市交通的实际状况实施动态分析，因此一般来说这种方法将两个枢纽间城市道路上的最短路径作为虚链接属性的主要部分。而货物在枢纽内的装卸费用和时间、存贮费用和时间成为虚链接属性的另一部分。这种虚链接的属性代表的是一个转运过程。

由于货物的目的地不同，其走行时间、距离、费用也就不同。另外，由于铁路发车时刻不同，货物的等待时间、费用也不同，因此需制作不同的虚链接来表示。例如，在运输大连→沈阳或者大连→哈尔滨的集装箱时，需进行转运，再由铁路运输至目的地。由于列车的发车时刻不一致，货物在转运枢纽的等待时间、存贮费用会不同，因此要制作不同的虚链接。

2.3 基于城市道路网的虚链接制作方法

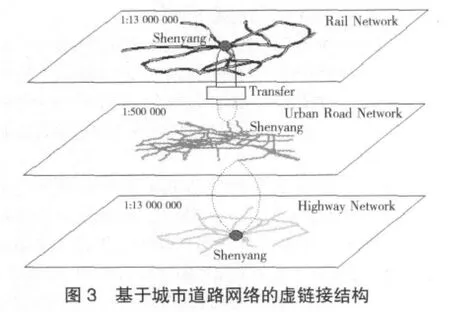
在逻辑结构上，超级运输网络模型由铁路子网络、公路子网络、城市道路子网络、转运枢纽和虚链接组成。在该网络中，铁路子网络与公路子网络处于平等地位，其信息表示的详细程度大致相当，属于宏观层次网络。而城市道路子网络表达的是城市内部的道路信息，属于微观层次网络。图3中的实线是虚链接，虚线表示的是两条道路直接相连，中间不存在阻碍，这是因为城市道路往往与城际公路直接相连，即卡车可由高速公路直接进入城市，然后经城市道路到达铁路货运站。

与之前介绍的虚链接相比，这一节中的虚链接表示货物的转运过程，转运线路在城市道路网络上表现出来。将城市内部原有的交通流与运输货物的卡车同时分配到城市道路网中，以便反映卡车的走行状态、路径选择以及阻抗等。由于网络模型会因为区域的变大而增加其规模，因此需简化城市道路网。

2.4 基于多尺度表达的虚链接表示方法

尺度是指数据表达的空间范围的相对大小和时间的相对长短，不同尺度所表达的信息密度不同[10]。不同的尺度导致不同的几何外形。我们采用两种尺度表现超级运输网络模型，如图4所示。这两个尺度上的虚链接分两层存储，第一层是宏观的存储结构，包括铁路子网络、公路子网络以及虚链接。第二层是微观的存储结构，包括城市内部的道路网络和表示转运枢纽信息的虚链接。宏观和微观层次间通过索引链接。

基于多尺度下虚链接构建的超级运输网络模型把前两种虚链接结合起来，把不同层面的城市道路网、公路网与铁路网衔接起来。这样的综合网络模型构建相关和互动机制将不同的子网络相互链接，一方面避免了因节点过多而造成的超级运输网络模型过于庞大；另一方面又能反映出货物在转运城市内部的走行状态。

3 各种网络模型的效绩评价

这里从网络的复杂性和对最短路径算法的适应性来检验三种超级网络的优劣。

3.1 最短路径算法分析

用基于属性的虚链接构建的超级网络与用基于城市道路子网络的虚链接构建的超级网络的物理结构完全相同，只是网络节点的个数不同，可以直接在这两种网络上使用Dijsktra算法。用基于多尺度表达的虚链接构建超级网络在物理结构上分为了两层，因此在搜索最短路径时需要进行分步求解，具体步骤如下：

第一步，在宏观层次的网络上，用Dijsktra算法求解最短路径。如果该路径中包括运输方式转换，那么得到的最短路径中会包括经过某换装节点的虚链接，记录这些虚连接，然后转入第二步；若不存在运输方式转换，则结束计算获得最短路径。

第二步，搜索最短路径中所有经过的虚链接，利用虚链接的索引获取城市道路子网络的信息，在城市道路子网络中，以进入城市道路子网络的节点为起始点，以转运枢纽为终点，再次运用Dijsktra算法，求解在城市道路子网络中的最短路径。

第三步，基于比例尺和索引把两个最短路径综合在一起，得到多尺度网络中两点间的最短路径。

3.2 实例分析

为了比较三种网络的效率，本文以大连港为中心，把东北地区作为整个研究对象，以大连、沈阳、长春、哈尔滨和满洲里为枢纽，建立海铁联运运输网络。该网络包括公路子网络、铁路子网络、虚链接以及转运枢纽，整个网络的链接见表1。可以看出第一种超级网络最简单，第三种超级网络最复杂。

针对同一个起终点（大连-哈尔滨），在三种网络上Dijsktra算法的时间分别为0.30s、0.62s和0.47s(CUP=Pentium 2.2G)。也就是说第一种网络需要的时间最少，因为网络的节点和链接数量少。第三种网络尽管结构复杂，但是计算时间要比第二种短很多。

4 基于超级网络的运输政策评价

这里归纳了11项改善集装箱运输的政策或技术，他们分别是：(1)开通集装线班列，大连←→沈阳、大连←→哈尔滨、沈阳←→满洲里；(2)使用双层的集装箱车辆；(3)增加班列的发车频率，将大连←→沈阳的发车频率由每周2班增加到每周3班，将沈阳←→满洲里的发车频率由不定期改为每周两班;(4)将列车的运行速度由60km/h提高到80km／h；(5)修建铁路货运专线；(6)优惠铁路的运价85%；(7)修建连接大连港口和铁路枢纽的高速公路；(8)在沈阳和哈尔滨建设集装箱场站；(9)使用先进的装卸设备；(10)为综合运输提供信息平台；(11)所有场站管理数字化。通过组合这些政策与技术，我们提出如下运输改善措施：

方案A=不做任何改善；方案B=(7)+(8)+(9)+(10)+(11)；方案C=(4)+(5)+(6);方案 D=(1)+(2)+(3);方案 E=(1)+(4)+(7);方案F=(1)+(2)+(4)+(5)+(7)+(8)+(9);方案G=(1)+(2)+(3)+(4)+(5)+(6)+(7)+(8)+(9)+(10)+(11)。

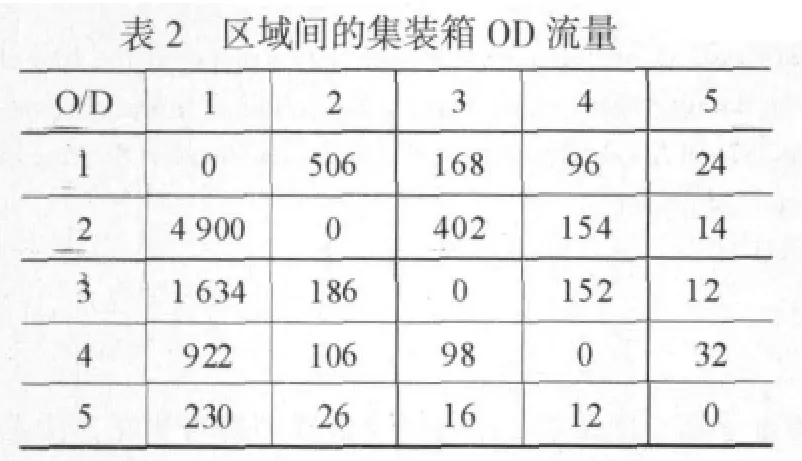
把大连、沈阳、长春、哈尔滨和满洲里设为5个运输小区如图5所示。由于无法直接知道5个小区间的集装箱OD流量，故利用从网站和城市统计年鉴上获得的零散集装箱运输量数据，配合重力模型估计得到每两周的集装箱O-D流量，见表2。根据最小费用原则把这个OD流量分配到与七个措施相对应的超级网络上，得到如表3所示的运输费用情况。

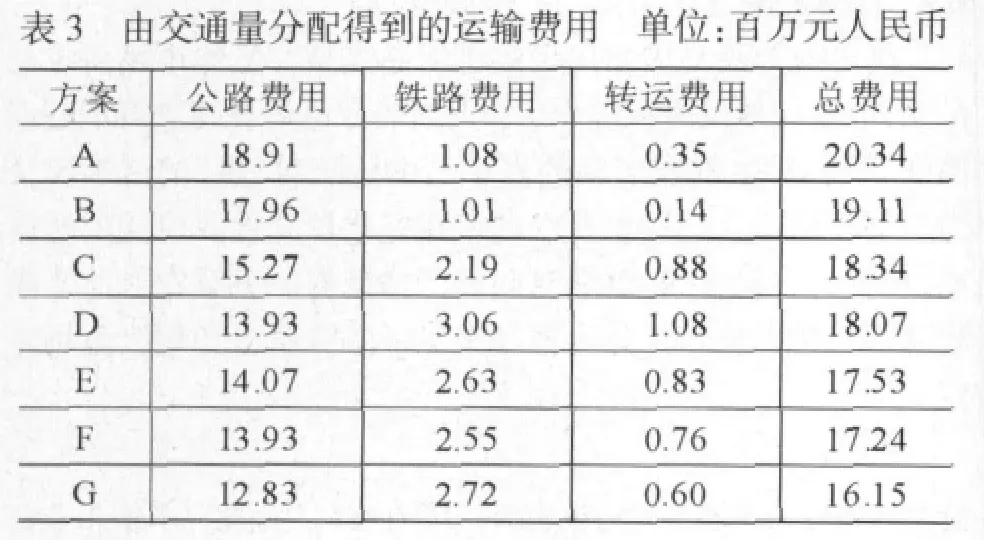
可以看出与不采取任何改善措施相比，方案B节约运输费用123万元，方案C节约运输费用200万元，方案D节约运输费用227万元。方案C和方案D比方案B比更加明显，是因为铁路能力增加了，这说明目前铁路的需求是旺盛的，但是供应能力达不到要求。由于方案B只改善了转运环节的设施和设备，因此虽然转运费用有所下降，但是转运量没有增加。方案E、方案F和方案G采用了一系列的政策和技术，其效果更加明显。通过比较可以知道单一的政策和技术的效果要比系列政策和技术的效果差，也就是说综合运输是一个大系统，只有各方面的全面合作，才能改善运输效率，节约运输成本。

5 结论

本文研究了超级运输网络中虚链接的概念和抽象方法，以及基于不同的虚链接构建超级运输网络模型的方法。在超级运输网络模型中转运枢纽被抽象为虚链接，文中提出三种形式的虚链接，并对用这三种虚链接构建的超级网络进行了性能评价。通过对最短路径算法的测试，我们发现用基于多尺度的虚链接构建的超级网络模型具有最好的性能，能够真实地反映网络中的换装行为。

我们还利用基于对尺度的虚链接的超级网络模型测试了改善综合运输效率与费用的政策与技术的实施效果。测试结果显示，铁路运输能力的增加可以节约运输成本，一系列的综合政策与技术要比单一的改善措施具有更大的效果。

[1]靳志宏，朴惠淑，杨华龙.集装箱多式联运系统装卸与运输一体化优化问题[J].系统工程，2005,23(11):1-6.

[2]郭子坚，王诺，霍红.多种运输模式下国内沿海集装箱港口布局模型研究[J].大连理工大学学报，2001,41（5）：598-601.

[3]王涛，王刚.一种多式联运网络运输方式的组合优化模式[J].中国工程科学,2005,7（10）：46-50.

[4]魏航，李军，刘凝子.一种求解时变网络下多式联运最短路的算法[J].中国管理科学,2006,14（4）：56-63.

[5]张建勇，郭耀煌.一种多式联运网络的最优分配模式研究[J].铁道学报，2002,24（4）：114-116.

[6]Nijkamp Peter, Reggiani Aura, TsangWai Fai. Comparative modelling ofinterregional transport flows: Applications to multimodal European freighttransport [J]. European Journal of Operational Research, 2004,155（3）:584- 602.

[7]Beuthe Michel,et al.Freight transportation demand elasticity's:a geographic multimodal transpiration network analysis[J].Transportation Research Part E,2001,37:253-266.

[8]South worth Frank,Peterson Bruce E..Intermodal and international freightnetwork modeling[J]. Transportation Research Part C, 2000,(8): 147- 166.

[9]Kozan E.Optimisingcontainertransfersatmultimodalterminals[J].Mathematical and Computer Modelling,2001,31(10):35- 243.

[10]胡最,闫浩文.空间数据的多尺度表达研究[J].兰州交通大学学报,2006,25(4):35-38.