基于核函数法进行拒绝推断的信用评分模型

魏秋萍，张景肖,张 波

0 引言

银行在利用历史数据创建信用评分模型时，能够采集到两大类客户群的数据：曾经被批准的申请人和曾经被拒绝的申请人的信息。对于曾经被批准的申请人，银行不仅有申请信息，还能根据其过去的表现判断其是好客户还是坏客户。而对于曾经被拒绝的申请人，银行除了知道他们的申请信息以外，无法知道他们是好还是坏客户。由于被拒绝的申请人信息缺失，在创建信用评分模型的时候这些样本的数据常常被忽略。而信用评分模型的应用对象应该是未来所有的申请人构成的总体，这个总体也称为入门总体[16]。由所有被接受的申请人构成的建模样本显然并不是总体的代表样本。这样如何推断那些曾经被拒绝的申请人的好坏定性并把他们也加入到建模样本中来，就是困扰信用评分领域多年的拒绝推断问题[12]。

对于拒绝推断问题的理论研究始于上个世纪70年代末，在过去的30年间，一些学者围绕是否该做拒绝推断以及如何做拒绝推断展开了研究。Hsia[12]基于假设P(default|X,rejected)=P(default|X,accepted)提出了用augmentation或re-weighting的方法来做拒绝推断。Heckman[11]首次提出了用双值型的二阶段模型来做拒绝推断。Boyes等[2]对信贷审批决策和违约模型这两个序贯事件创建双值型的probit模型，以此避免了样本偏差。Poirier[17]认为如果不引入一个额外的数据集则不可能评估由于样本偏差带来的损失。Hand等[10]深入研究了拒绝推断问题，他们认为除非对好坏客户的违约分布做出额外的假设，否则拒绝推断问题并不能起作用。Joanes[14]首先针对被接受的申请人组成的样本用logistic回归创建信用评分模型，然后应用到被拒绝的申请人来做拒绝推断。Copas和Li[6]认为非随机缺失问题导致绝大多数统计方法难以用来解决拒绝推断问题。 Feelder[9]用EM（Expectation-Maximizarion）算法把拒绝推断作为缺失值填补来处理，他考虑了非随机缺失的情况，也就是被接受样本和拒绝样本的违约概率分布是不同的，但是他提出的算法使用了随机缺失的假设。Chen和Åstebro[4]认为被接受的样本可以代表所有申请人这个总体，不需要做拒绝推断；被接受的样本和被拒绝的样本中好客户的比例是一样的和接受样本和拒绝样本中的违约分布不同需要拒绝推断。Feelders[9]指出解决拒绝推断唯一的方法是双值型二阶段模型，该方法曾经被认为是无效的。Ash和Meester[1]建议使用信用局数据，通过考察被拒绝的申请人在其它银行的表现来推断他到底是好客户还是坏客户。Jacobson和Roszbach[13]用实证分析说明了P(default|X,rejected)不等于 P(default|X,accepted)，并且用双值型的Probit模型创建了信用评分模型。Banasik、Crook和Thomas[8]用模拟数据讨论了信用评分模型中的样本偏差。Crook和Banasik[7]研究了重抽样和外推法的效率，认为这些技巧并没有比只是使用被接受客户的模型要好。Verstraeten等[20]通过实证分析来探索信用评分模型中的样本偏差。Kim和Sohn[19]用双值型模型来做拒绝推断，他们的结论表明，只是使用被接受的客户创建模型的确存在样本偏差，拒绝推断可以提高模型的效果但是并不能完全解决样本偏差的问题。Banasik和Crook[2]试图探索Heckman样本选择模型和改变样本权重是否可以改善模型的预测能力，但是实证研究表明这两种方法单独或者结合起来使用都只有微小的成效。

对于信用评分模型中建模样本的偏差（称为拒绝偏差（Reject Bias））[18]:173，是否需要通过拒绝推断来校正以及到底如何做拒绝推断，到目前为止并没有一个定论。但是这个问题对于提升信用评分模型的预测准确性有极其重要的意义，值得进一步的研究和探讨。

1 拒绝推断的理论价值

可以把被接受的申请人组成的样本称为接受样本，把被拒绝的申请人组成的样本称为拒绝样本。毋庸置疑，接受样本和拒绝样本中都有真正的好客户和坏客户。假设接受样本中的好客户的数量用nag，坏客户的数量用nab来表示，拒绝样本中的好客户的数量用nrg，坏客户的数量用nrb来表示。

信用评分模型采用的模型大都可以用

这个一般形式来概括，其中 pt=P(yt=1|xt)或者pt=P(yt=0|xt)。因此，模型的优比：

是模型参数估计过程中必须重视的参数之一。如果建模样本只是使用接受样本，则该样本中好坏客户发生比odds1=nag/nab。如果建模样本中同时使用了接受样本和拒绝样本，即建模过程中使用了拒绝推断的技术，则该样本中好坏客户的发生比为

无论是接受样本还是拒绝样本，其中的客户都是通过一定的审批机制来决定到底是被接受还是被拒绝的。这个审批机制可能是一个专家评分模型也可能是原先的信用评分模型。拒绝推断是否必要和这个原先的审批机制不无干系。下面分三种情形来探讨拒绝推断的必要性。

情景1：原有的审批机制完全无效，拒绝样本中的申请人是完全随机抽取的。因此坏客户在接受样本和拒绝样本中随机等可能出现的，这两个样本中的好坏客户比（odds）是相等的，即

可得 nagnrb=nrgnab。所以

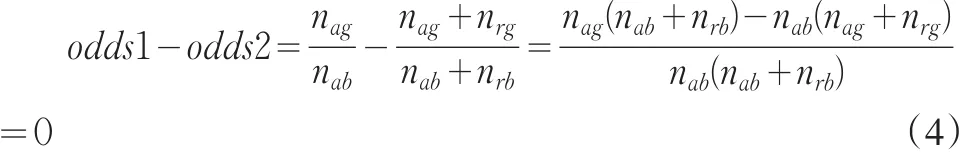
因此，在原有的审批机制完全无效的情况下，是否使用拒绝推断对模型的预测效果没有任何影响。

情景2：原有的审批机制完全有效，基于其做出的决策也是完全正确的，也就是接受样本中全是好客户，而拒绝样本中全是坏客户，即nab=0,nrg=0，所以

如果只是使用被接受客户建模，就会错误的认为所有的申请人都是好客户，这显然不符合逻辑。只有把被拒绝客户也加入进来构建新的建模样本才会有比较合理的好坏客户比

尽管这种情形是一个非常理想的状态，一般不可能在现实中出现，但是在这种情况下拒绝推断是非常必要的。

情景3：原有的审批机制是有效的，接受样本中绝大多数是好客户，拒绝样本中绝大多数是坏客户。一般来说，在实际应用过程中，银行会把评分从高到底排序分成若干个评分池[22]。具体来说，假如某评分模型分成了i+j个评分池，如果某个申请人的评分落在了第1,2,…,i个评分池中，则表明他可以被批准；如果其评分落在了第i+1,i+2,…,i+j个评分池中，则表明他应该被拒绝。一个有效的评分模型能够保证分数高的评分池中的好坏客户比要大于分数低的评分池中的好坏客户比，即

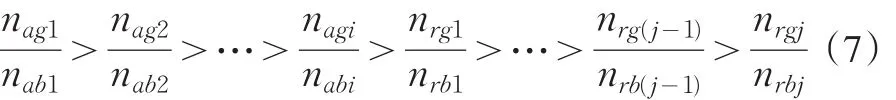
在这种情况下，可以证明

也就是只是使用接受样本的好坏比要大于使用了拒绝推断的建模样本中的好坏比。

证明：（8）的证明可以用不完全归纳法。

假设当i=k,j=l时，odds1＞odds2成立，可以令

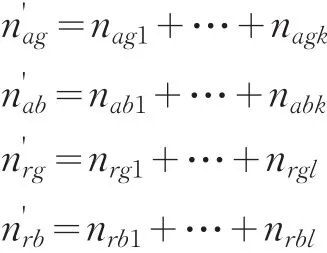
则有

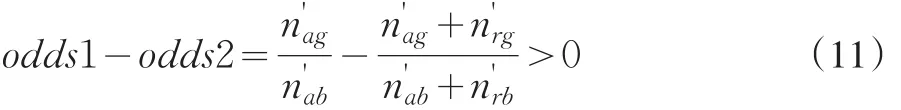
且

则当i=k+1,j=l+1时，有

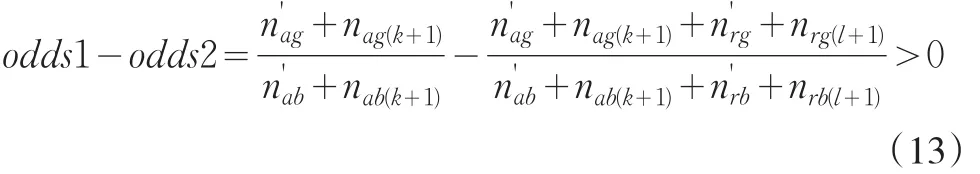
也成立。证毕。

所以，（8）式成立，当原先的审批机制是有效的时，odds1＞odds2肯定成立，拒绝推断是需要的。

综上所述，除非原有的审批机制完全无效，否则拒绝推断就是必要的。从原先的审批机制出发，根据是否使用拒绝推断的建模样本的优比比较，不难分析出，在实际应用中，必须使用拒绝推断技术来校正被接受样本和总体的样本偏差。

2 核函数推断法在拒绝推断中的应用

信用评分模型的拒绝推断是要推断出拒绝样本中那些被拒绝的申请人到底是好客户还是坏客户。从理论的角度看，这就是缺失值处理问题。如何做拒绝推断，可以通过分析三类缺失值的产生机制[15]来进行讨论。

令y=1表示某个申请人会成为坏客户，y=0表示该申请人的确是好客户；令a=1表示该申请人在过去得到审批通过，而a=0表示该申请人曾经被拒绝。三类缺失值产生的机制如下：

①完全随机缺失(Missing completely at random(MCAR))：当好坏客户标识y被观测到的概率不依赖于y的值也不依赖于预测变量组X的值时，即

则y缺失就是完全随机缺失。

②随机缺失(Missing at Random(MAR))：当好坏客户标志y被观测到也就是a=1的概率不依赖于y的值，但是会依赖于预测变量组X的值时，即

则y如果缺失就是随机缺失。

③非随机缺失(Missing not at Random(MNAR))：当好坏客户标志y被观测到也就是a=1的概率既依赖于y的值，又依赖于预测变量组X的值时，即

则y如果缺失就是非随机缺失。

完全有效的审批机制和完全无效的审批机制在在实际中一般不会出现。而有效的审批机制对应的是非随机缺失。因此，从推断法的角度来解决信用评分领域的拒绝推断问题，就是要解决非随机缺失因变量的缺失值填补问题。基于此，核函数推断法是一种可以用来尝试解决信用评分模型的拒绝推断问题的一种方法。

Cheng[5]和Wang[21]都曾经用核分布来对缺失的响应变量做出补缺处理。因为响应变量是自变量的函数，估计响应变量的值就是估计

其核估计为

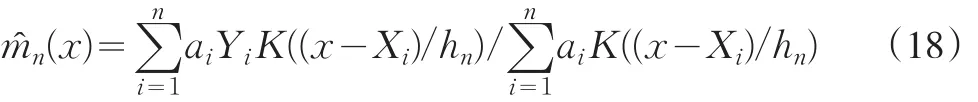
这里，K((x-Xi)/hn)是核函数，hn是核函数的光滑参数，也称为带宽，当n→∞时，带宽hn→0。核函数的选择可以根据具体情况而定，在以往的研究中，常用正态函数、三角函数和二次函数等对称的概率密度函数作为核函数。

核函数补缺恰好解决了非随机缺失的缺失值补充问题。在信用评分模型的建模样本中，每一个观测都搜集有三方面的因素(Xi,Yi,ai)(i=1,2,...,n)。其中，Xi=(x1i,x2i,…,xdi)是一个d维的向量，该因素基本都能够观测到，当ai=1时Yi能够观测到，当ai=0时Yi不能观测到。由于这里的因变量是离散变量，可以选择示性函数I(x=Xi)作为核函数，即

因此，可用的核估计为

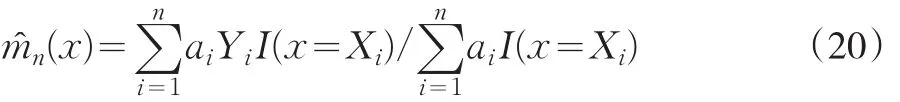
在信用评分模型的开发过程中，可获得的自变量的个数很多，如果用示性函数I(x=Xi)作为核函数，就会遭遇维度的诅咒。自变量个数越多，两条观测完全相同的概率就越小，则I(x=Xi)几乎都为0，核估计没有意义，这对于拒绝推断这个实际应用没有任何帮助。为了避免维度的诅咒带来的影响，必须对核函数的形式做一些调整，有以下可以使用的调整方法：

（1）最相似法

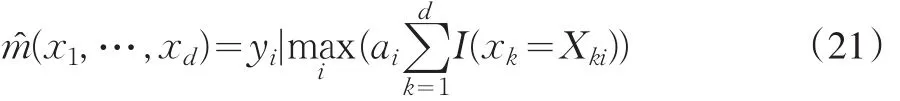
即，对于每个被拒绝的申请人，首先把他的d个自变量和样本中所有被批准的申请人的d个自变量分别作比较，如果双方的第k个自变量相同则取1，否则取0。然后再把这d个判断值相加得到，则核估计的取值与使得最大的那个被批准的申请人的因变量的取值相同。这种推断方法的思想就是为每一个被拒绝的申请人寻找在特征上最相似的被批准的申请人，看他到底是好客户还是坏客户，以此决定这个被拒绝的申请人到底是好客户还是坏客户。最相似法的核估计的取值只有0或者1，可以直接作为被拒绝的申请人的因变量的取值，不需要任何对于拒绝样本的先验信息。

（2）加权平均法

即对于每个被拒绝的申请人，首先把他的d个自变量和样本中所有被批准的申请人的d个自变量分别作比较，如果双方的第k个自变量相同则取1不同则取0，然后再把这d个判断值相加得到，然后再求出这种推断法的思想就是用特征的相似程度作为权重，以样本中被批准的申请人的因变量取值做加权平均得到这个被拒绝的申请人的核估计取值。在信用评分模型中，因变量是取值为1或0的离散变量，而加权平均法中因变量的核估计是介于0和1之间的数，因变量的核估计并不能直接作为因变量的值。这时就需要被拒绝样本中坏客户占比的先验信息百分之π0，然后选择核估计为从高到低排序前百分之π0的观测的因变量的取值为1，其余观测的因变量取值为0。

（3）Q1加权平均法

这种核函数推断法的思想和加权平均法的相类似，主要区别在于：不是取所有被批准的申请人，而是根据特征的相似程度选择被批准的申请人的前百分之一，随后的处理方法与加权平均法相似，求因变量的加权平均值作为一个被拒绝的申请人的核估计取值。同样，Q1加权平均法中因变量的核估计并不能直接作为因变量的值。这时就需要被拒绝样本中坏客户占比的先验信息百分之π0，然后选择核估计为从高到低排序前百分之π0的观测的因变量的取值为1，其余观测的因变量取值为0。

3 实证分析

对拒绝推断问题进行实证研究面临的最大困难是数据，要获得被拒绝的申请人到底是好坏客户的结论只有两种途径：一是利用实验设计，选择某些本应被拒绝的申请人给予批准，并通过严密的跟踪监控来确认到底是好客户还是坏客户。这种方法有很大的风险，将会给银行的风险控制带来巨大的挑战；二是查询人行征信信息，根据被拒绝的客户在其它银行的表现来决定其到底是好客户还是坏客户。这种方法比较耗费人力，并且不能保证查到所有被拒绝的申请人的征信记录。

本文利用某银行信用卡业务的数据来做拒绝推断的实证研究，拒绝样本中的申请人到底是好客户还是坏客户是通过实验设计的思路判断得出的。接受样本的样本量为12292，其中好坏客户比为96.75：3.25；拒绝样本的样本量为8250条记录，其中好坏客户比为81.7：18.3。验证样本有12325条记录，其中好坏客户比为90.7：9.3，验证样本相当于入门总体的有效代表。

可以设计如下的方法来做拒绝推断的实证分析研究：

（1）不做拒绝推断，只是使用接受样本创建信用评分模型，并用验证样本做模型效果的验证。

（2）用三种核函数推断法对拒绝样本做拒绝推断，并把推断出因变量取值的拒绝样本和接受样本汇总后再创建信用评分模型，然后利用验证样本做模型效果的验证。这里，对于每一种核函数推断法又有三种子方案：①选择样本中的全部自变量（25个）做核函数推断；②选择部分精选的自变量（18个）做核函数推断；③选择全部自变量（25个）做核函数推断。为了避免自变量的取值过于分散而导致核函数全部为0，在这里对自变量做了分组处理，分组方法参考信用评分领域常用的信息量IV值IV=(p1-p0)*ln(p1/p0)，把连续变量分成若干个区间和压缩分类变量的类别时都要保证信息量的损失尽可能的小。

（3）用信用评分领域的打包（Parcelling）方法来对拒绝样本做拒绝推断，并把推断出因变量取值的拒绝样本和接受样本汇总后再创建信用评分模型，然后利用验证样本做模型效果验证。打包方法首先利用接受样本创建初步的信用评分模型，并把预测概率排序分组，然后给拒绝样本中的申请人打分，并对打分得到的预测概率按照接受样本中的预测概率分组规则进行分组。该方法假设在同一概率组中，拒绝样本中的坏客户比例是相对应的接受样本中坏客户比例的若干倍，这个倍数就叫做事件增长率。事件增长率需要业务人员根据经验给出估计，是一种先验信息。

（4）用信用评分领域的硬截止的方法做拒绝推断，并把推断出因变量取值的拒绝样本和接受样本汇总后再创建信用评分模型，然后利验证样本做模型效果验证。硬截止方法首先利用接受样本创建信用评分模型，并据此给拒绝样本中的申请人打分。该方法假设得分高于某个临界值的为好客户，低于临界值的为坏客户，这里的临界值也需要业务人员给出坏客户率的先验估计。

（5）把外部数据加入建模样本中然后创建模型，然后利用验证样本做模型效果验证。这里的外部数据是通过实验设计获得的被拒绝申请人到底是好客户还是坏客户的信息。

具体结果如表1。

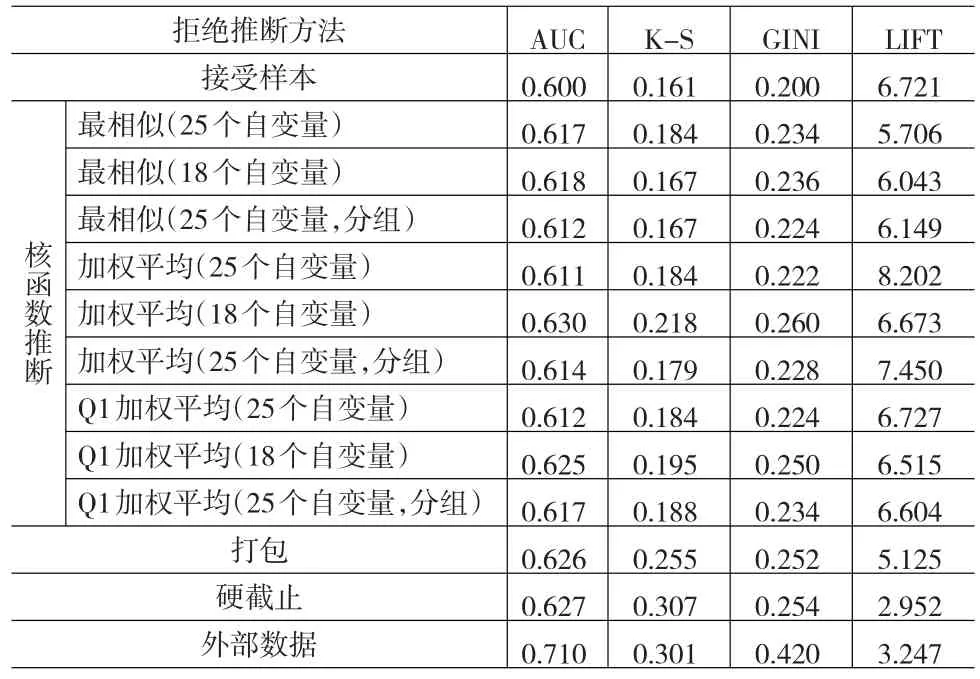
表1 拒绝推断的实证分析

根据实证分析的结果可知：

（1）由于样本数据的限制，拒绝推断的实证分析结果并不是很理想，除了Lift值以外，AUC统计量、K-S统计量和GINI系数的值都偏小，这表明该模型的预测准确性相对偏低。

（2）三种核函数拒绝推断法都能提升模型的预测准确性，相对来说，加权平均法的提升能力最强。利用18个自变量做核函数推断的加权平均法的AUC和GINI系数的值仅次于利用外部数据的验证值。同时这三种核函数推断法对模型的影响取决于用于核估计的自变量X是否就是真正影响因变量的因素，也取决于这些自变量的取值是否集中。如果用于做核函数估计的自变量选择的好，能大大提高拒绝推断的准确性并提高模型的预测能力。实证分析的结果也表明，选择18个精选自变量做核函数推断的方法普遍要好于使用25个自变量的验证结果。因此，利用核函数推断方法做拒绝推断时，选准了自变量可以取得更加理想的效果。

（3）打包法和硬截止法也都提升了模型的预测效果。但是，打包方法受事件增加率影响，硬截止方法受临界值的影响，临界值选的好才能保证提升的幅度。

（4）使用外部数据来做拒绝推断的验证指标的值最大，它是提升信用评分模型预测准确性的最有效方法。

q总而言之，使用外部数据来获取真实信息是最有效的拒绝推断方法，但是这种方法也最耗费人力和物力，银行一般不愿意承担获取真实信息的风险和成本，该种方法适合小范围的推断。核函数推断法、打包法和硬截止法都能在一定程度上提升模型的预测效果，但是这些方法基本都需要事先知道坏客户率这个先验信息，必须依赖于业务人员的经验。相对来说，核函数推断法在业务逻辑上更易于理解，利用精选的自变量对拒绝样本中的申请人做核函数推断能获得比较理想的推断效果，可以作为一种新的拒绝推断方法应用于实际中。

4 小结

被接受的申请人构成的样本是所有申请人这个总体的有偏样本，用被接受的申请人组成的样本创建的信用评分模型存在样本偏差。为了获得更准确的预测结果，必须要做拒绝推断来校正这种偏差。

通常情况下，当对接受样本和拒绝样本所做的一些总体假设正确有效时，拒绝推断方法一般都能够提高模型的预测准确性，但是准确性的提升幅度往往受可获得信息的制约。人民银行征信数据或者银行自身的实验设计都能提供额外的信息使得拒绝推断更加合理，从而保证信用评分模型更加准确更加合理。人行征信数据可以免除商业银行为了获得拒绝样本的信息而承担的风险，是更加可取的方法，在国内大力推广人行征信体系意义重大。由于中国的人行征信体系目前还处于发展过程中，核函数推断法是现阶段可行的拒绝推断替代方法。

[1]Ash D.,Meester S.Best Practices in Reject Inference,Presentation at Credit Risk Modeling and Decision Conference[Z].Wharton Financial Institutions Center,Philadelphia,2002.

[2]Banasik J.,Crook J.Reject Inference,Augmentation,and Sample Se⁃lection[J].European Journal of Operational Research,2007,(183).

[3]Boyes W.J.,Hoffman D.L.,Low,S.A.An Econometric Analysis of the Bank Credit Scoring Problem[J].Journal of Econometrics,1989，3～14.

[4]Chen G.,Åstebro T.Bound and Collapse Bayesian Reject Inference when Dataare Missingnot at Random[R].University of Toronto,2006.

[5]Cheng Philip E.Nonparametric Estimation of Mean Functional with Data Missing at Random[J].Journal of the American Statistical Associ⁃ation,1994,89(425).

[6]Copas J.B.,Li H.G.Inference for Non-random Samples[J].Journal of the Royal Statistical Society,B,1997,(59).

[7]Crook J.,Banasik J.Does Reject Inference Really Improve the Perfor⁃mance of Application Scoring Models[J].Journal of Banking and Fi⁃nance,2004,(28).

[8]Crook,J.,Banasik,J.,Thomas,L.C.Sample Selection Bias in Credit Scoring Models[J].Journal of the Operational Research Society,2003,(54).

[9]Feelders A.J.An Overview of Model Based Reject Inference for Cred⁃it Scoring[R].Technical Report,Utrecht University,Institute for Infor⁃mation and Computing Sciences,2003.

[10]Hand M.D.J.,Sebastiani P.,Henley W.E.Inference about Rejected Cases in Discriminant Analysis.In New Approaches in Classifica⁃tion and Data Analysis[M].New York:Springer,1994.

[11]Heckman J.J.Sample Selection Bias as a Specification Error[J].Econometrica,1979,47(1).

[12]Hsia D.C.Credit Scoring and the Equal Credit Opportunity Act[J].The Hastings Law Journal,1978,(30).

[13]Jacobson Tor,Kasper F.Roszbach.Evaluating Bank Lending Policy and Consumer Credit Risk[J].Computational Finance,1999,(3).

[14]Joanes D.N.Reject Inference Applied to Logistic Regression for Cred⁃it Scoring[J].IMA Journal of Mathematics Applied in Business and Industry,1993,5(4).

[15]Little R.J.A.,Rubin D.B.Statistical Analysis with Missing Data[M].New York:John Wiley&Sons,1987.

[16]Naeem Siddiqi.Credit Risk Scorecards[M].JNew York:ohn Wiley&Sons,2006.

[17]Poirier,Dale J.Partial Observability in Bivariate Probit Model[J].Journal of Econometrics,1980,(12).

[18]Lyn C.Thomas,David B.,Edelman,Jonathan N.Crook.信用评分及其应用[M].北京：中国金融出版社,2006.

[19]Kim Y.,Sohn S.Y.Technology Scoring Model Considering Rejected Applicantsand Effect of Reject Inference[J].Journal of the Operation⁃al Research Society,2007,(58).

[20]Verstraeten G,Van Den Poel D.The Impact of Sample Bias on Con⁃sumer Credit Scoring Performance and Profitability[J].Journal of the Operational Research Society,2005,(56).

[21]Wang Qihua,et al.Empirical Likelihood-Based Inference under Im⁃putation for Missing Response Data[J].The Annals of Statistics,2002,(30).

[22]陈建.信用评分模型技术与应用[M].北京：中国财政经济出版社,2005.

[23]王济川等.Logistic回归模型——方法与应用[M].北京:高等教育出版社,2001.