曲面笔式加工刀位点曲线的实时拟合*

孟书云

(南京工程学院自动化学院，江苏南京211167)

复杂曲面常规加工是将刀位点轨迹处理成大量直线或圆弧组成的加工代码，由CNC系统内简单曲线插补功能，生成控制指令来驱动伺服系统。这会使加工代码量巨大，机床需频繁加减速以及出现加工表面不光顺等问题［1－3］。

为避免上述问题，Yang等提出了基于离散刀位点的复合刀具路径生成方法［4］;Kang等给出了基于最小二乘法的采用B样条精确拟合刀位点轨迹的方法［5］;上述方法未提及离散刀位点的来源，同时为达到拟合的高精度，需进行迭代计算，运算量较大，存在迭代不收敛的可能性。Zhao等利用B3数学模型实现了数控加工刀位点轨迹规划，在反求控制定点时涉及求取边界切矢，而拟合曲线对边界条件敏感，选取不当会使拟合曲线畸变［6］;Chen等面向三角网格曲面提出了圆弧样条刀轨生成方法，但仅局限于三角片型曲面的刀路规划［7］。

针对复杂曲面笔式加工，提出一种刀位点轨迹实时高精度生成算法:根据插补器中读入的曲面、刀触点等几何信息以及刀具、加工余量等工艺信息，用三次B样条曲线实时重构刀位点轨迹线，来高精度逼近理想刀位点轨迹。

1 曲线数学模型

曲面笔式加工以曲面局部区域为加工对象，即刀具路径在指定的曲面局部加工区域上进行规划。以曲面上某一点的法矢量作为投影方向，将一族空间自由曲线作平移旋转变换，使投影后的一系列曲线能正好落在曲面待加工的局部区域上。

如图1所示，以三次B样条方法描述的初始导引线P(m)，经旋转平移变换后，再绕曲面在投影处法矢量旋转，得到目标导引线Q(m)。

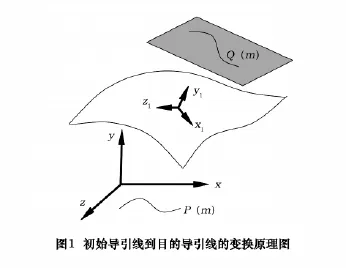
将目标导引线Q(m)沿曲面上投影点的法矢量映射，最终投影在曲面上的曲线才是实际加工时的刀触点迹线。复杂曲面多采用参数形式描述，故提出的算法以参数式曲面作为研究对象，表示为2个变数u、v的单值函数S(u，v)。设单位投影矢量为O，其刀触点迹线可表示为

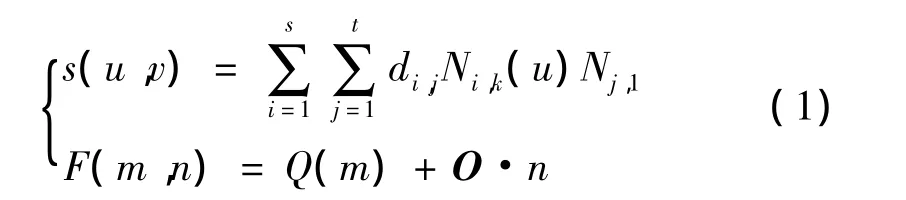
其中:F(m，n)为由目的导动线形成的参数式导动曲面;m、n为该曲面的2个参数(a≤m≤b，－∞ ＜n＜+∞)，并以三次B样条方法描述的参数式曲面S(u，v)作为笔式加工的对象;di，j为曲面的控制顶点;s、t分别为参数u和参数v方向上的控制顶点数。

2 刀位点数据的获取

由式(1)可看出，刀触点迹线由待加工曲面和一族导动曲面的交线族组成。由于待加工曲面和导动曲面的数学描述都是关于参数的高次耦合表达式，故无法直接得到交线的数学表达式。

为此，从目的导引线出发，据其和刀触点迹线之间的几何和运动学关系，找到两者之间的联系。由于目的导引线与初始导引线之间存在一一映射的关系，故初始导引线和曲面上的自由曲线型刀触点迹线之间亦存在一一对应关系。

如图2所示，目的导引线Q(m)和刀触点轨迹线L(u)是一对空间曲线偶。当加工的刀具沿L(u)运动到某点A时，在目的导引线Q(m)上必存在唯一一点B与之相对应，将点A和点B称为点偶。

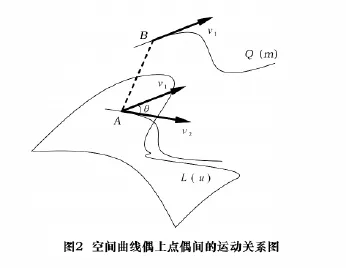
设刀具在刀触点迹线(即S(u，v)和F(m，n)交线)A处速度为v2，而目的导引线上对应点B处速度为v1，两速度矢量之间的夹角为θ，则

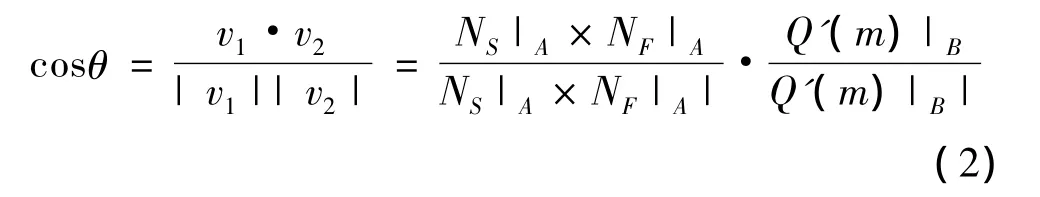
其中NS|A和NF|A分别表示曲面 S(u，v)和 F(m，n)在点A处法矢量;Q′(m)|B表示目的导引线在点B处的切矢量。

设插补进给速度为V，时间用t表示，由于时间增量非常小，故可以将两参数曲面交线的弧长ds对时间的微分近似为插补进给速度，即

刀具沿该刀触点迹线加工时，若保持刀触点速度的恒定，就能保证恒定的材料去除率，有利于曲面加工质量的提高。

为简化计算，将速度矢量v1和v2及两者夹角θ构成的一般三角形近似为直角三角形，则

而目的导引线Q(m)上的微段曲线关于时间t的一阶导数，有:

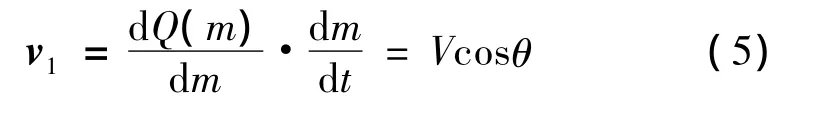
同理可求出参数m关于时间t的二阶导数。

从初始导动曲线P(m)(a≤m≤b)出发，考虑该曲线关于插补周期Δt的Taylor展开式。设曲线上当前点对应的参数值为mk，下一点对应的参数值为mk+1，则

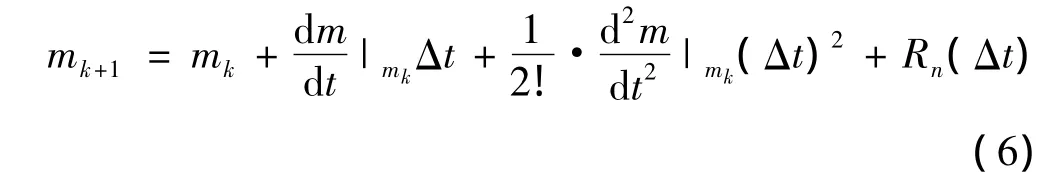
其中:Rn(Δt)是Taylor展开式的高次项。当曲线P(m)的曲率不是很小时，可以将mk+1的值只取至一次项。至此，求出了刀触点轨迹线上相邻刀触点在初始导引线上对应点的参数值。

将式(6)求得的参数值代入式(1)，可反求出刀触点迹线的点在曲面上对应的(u，v)值，进而得到该点的坐标值。

目前大多数数控系统具有刀补功能，可直接用刀触点坐标插补加工，但当加工自由曲面类零件时，直接用刀补功能将产生较大的误差，需计算刀心轨迹，故需根据上述有序离散刀触点及曲面、刀具等工艺信息，得到一组有序离散刀位点，进而完成刀心轨迹的计算。

3 刀位点轨迹实时高精度构造

在刀位点序列(已剔除产生干涉的刀位点)中每隔一个时间段顺次取出4个点，分段拟合理想刀位点轨迹线。每次拟合计算以连续4个刀位点作为输入。如图3所示，为提高刀位点轨迹拟合精度，采取“去两边，取中间”的策略，使用三次B样条曲线作为拟合曲线数学模型，即连续4个刀位点Pi(i=0，1，…，3)可反求出6个控制顶点，其决定的曲线如图3中细实线所示(首末控制顶点分别为P0、P3，其余控制顶点di(i=1，…，4)用“Δ”表示)。

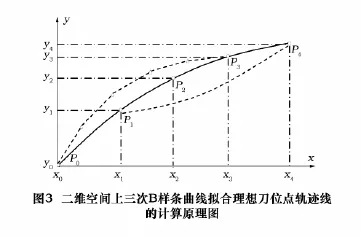
每顺序4个控制顶点决定一个节点区间上的曲线段。生成的3段三次B样条曲线段，保留中间一段，即控制顶点di(i=1，…，4)生成的曲线段，作为对刀位点数据P1、P2之间理想刀位点轨迹线的拟合。对于刀位点P2、P3之间的理想刀位点轨迹，由过 Pi(i=0，1，…，3)的三次B样条曲线拟合，保留位于P2、P3之间的曲线段，依此类推。

在对刀位点数据进行拟合时，有两个问题需要解决:一个是如何进行准确的参数化得到合适的节点矢量;另一个是如何确定恰当的边界条件作为补充条件，用于控制顶点的求取。

显然，这些有序刀位点数据确定的理想刀位点迹线的弧长是个未知量。由文献［8］可知，利用通过相邻刀位点且弦高为δ(即刀心轨迹的加工精度)的圆弧段弧长来近似理想刀位点迹线的弧长，即使用近似圆弧法参数化方法，比使用均匀节点法、向心法和累积弦长法要更加精确。

设相邻刀位点Pi、Pi+1的连线长度为L，则近似圆弧段的圆弧半径为

圆弧弧长S为

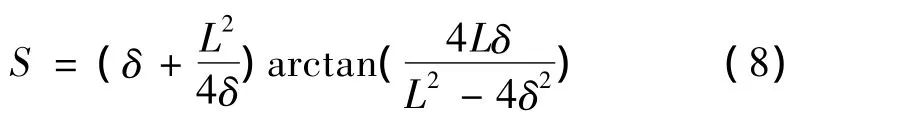
为保证拟合的三次B样条曲线通过给定的4个连续刀位点 Pi(i=j，j+1，…，j+3)，以近似圆弧参数化法求得的参数矢量，需在参数区间端点设置重节点并进行归一处理。

设输入的4个刀位点数据为Pi(i=0，1，…，3)以及单位切矢量˙Pi(i=0，…，3)。由样条曲线性质可知，有6个控制顶点di(i=0，1，…，5)待求，而归一化后的节点矢量为 U=［0，0，0，0，u4，u5，1，1，1，1］，其中

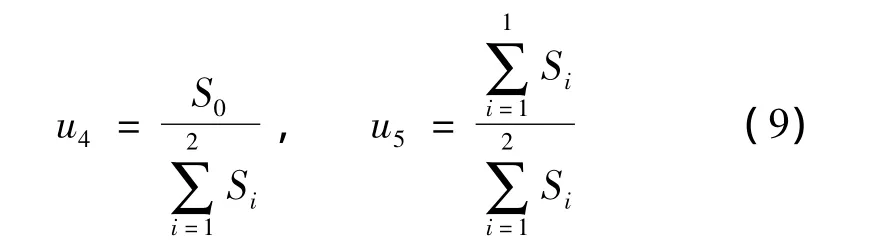
每次计算，仅需更新u4、u5即可。

对于本问题，求解用于拟合的三次B样条曲线控制顶点的方程组可表示为

其中:Ni，3(ui)(i=0，1，…，3)是节点区间端点处的三次四阶B样条基函数。由基函数递推公式可知，非零值共3个，由于采用了近似圆弧参数化，每个基函数的值需实时计算。

由已知条件得知式(10)解不确定，需再补充2个条件，拟通过曲线两端切矢条件建立边界约束。由刀触点迹线和刀心轨迹的形成过程可知，用于拟合的三次B样条曲线，在每个有序离散刀位点处的切矢方向是可求的，但模长不易确定，而不恰当的模长通过反求得到的刀心轨迹存在畸变的可能［9］。

根据曲线的微分几何理论［10］，曲线的弧长是自身的不变量，选取弧长作为参数来描述曲线，有使曲线上每一点处切向量为单位向量的性质。而近似圆弧参数化方法可以使得拟合的曲线上每一点的切矢量近似为单位切矢。

由于节点矢量U={ui}，i=0，…，9，假设算子=ui+j－ui，而刀心轨迹L(u)在指定参数处的切矢量分别为

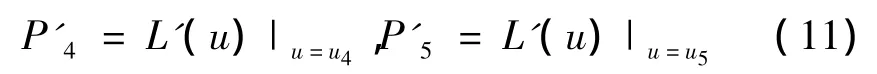
则补充的两个条件为

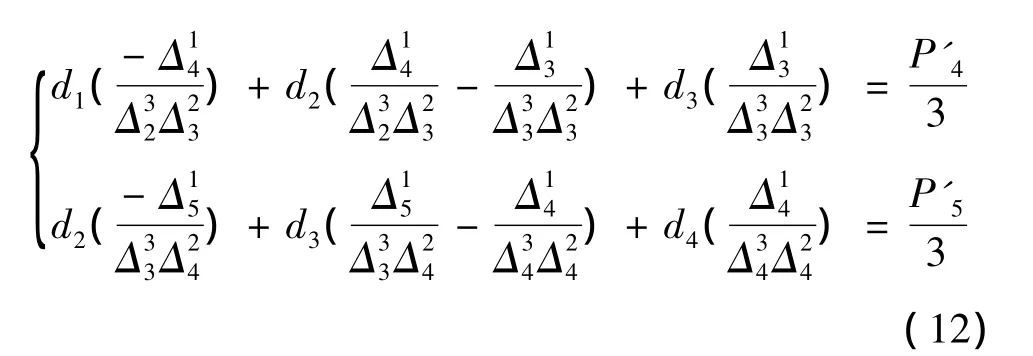
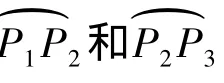
4 实例分析

研究测试加工对象如图4所示，被加工曲面采用三次B样条方法描述，曲面控制顶点坐标数据列于表1中，长宽高分别为120 mm×120 mm×55 mm。

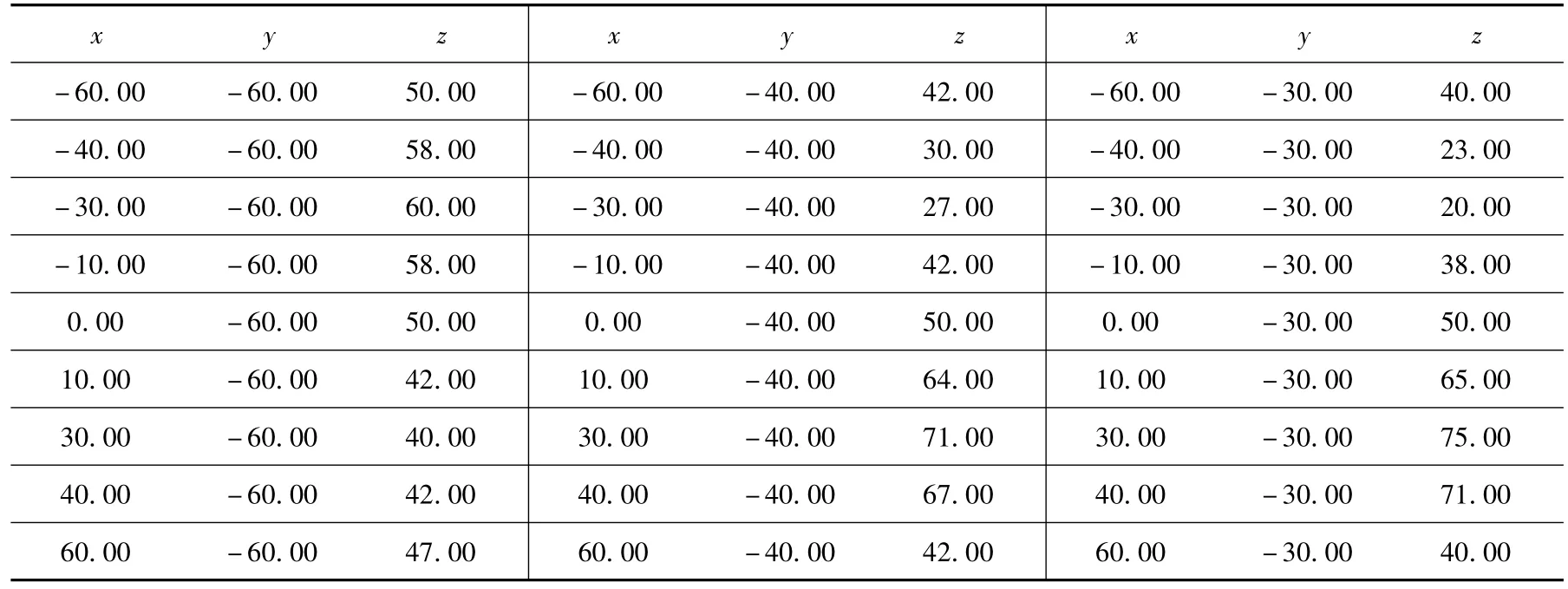
表1 曲面部分控制顶点坐标数据表 mm

设定加工进给速度为3 000 mm/min，插补周期为8 ms。将平面上的梅花和字符组成的组合图案，经平移旋转变换调整到合适的状态，投影到该曲面上，生成刀触点轨迹如图4所示。部分刀触点相关数据列于表2中。以刀头直径为3 mm的球头刀为加工刀具，沿刀触点处曲面外法矢量方向作为偏置方向，得到有序的离散刀位点数据系列。

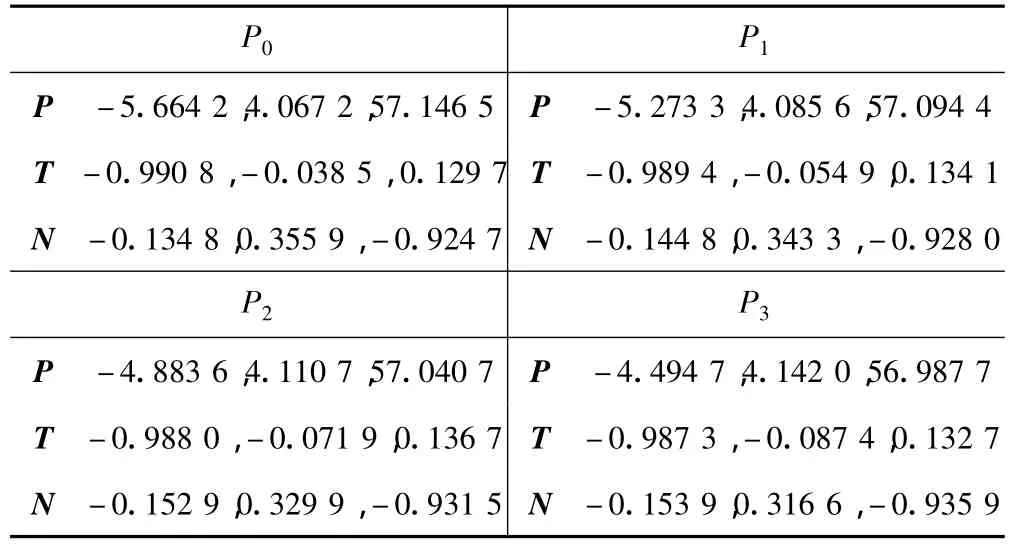
表2 部分刀触点相关数据表 mm

在CPU主频为1.66 GHz，内存为1 M的硬件环境以及Windows XP操作系统环境下，基于Visual C++6.0软件开发平台，由给出的算法对有序离散刀位点进行三次B样条曲线逐段拟合，每4个刀位点反求6个控制顶点所需时间列于表3中，平均用时0.014 ms。

表3 离散刀位点反求所需时间表 ms

与传统的大量连续直线段作为刀心迹线相比，采用三次B样条曲线拟合刀位点迹线带来的曲面轮廓误差如图5所示。

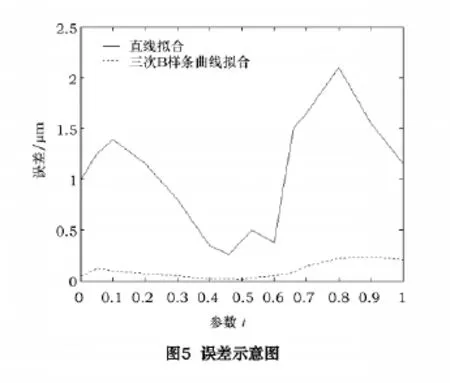
因三次B样条拟合严格通过所给定的刀位点，故加工时在这些点是没有误差的。与直接将离散刀位点顺序连接形成的直线段作为刀心迹线相比，采用三次B样条拟合刀心迹线，弓高误差明显减小。

5 结语

文中探讨了复杂曲面笔式加工时，使用三次B样条曲线实时高精度逼近理想刀位点轨迹的算法。算法的实现有利于对自由曲线轨迹进行高精度控制，大幅减少了加工代码量和内存占用量，为自由曲面的高精密加工奠定了理论基础。关于实时剔除会产生干涉的刀位点的算法，仍以顺次4个刀位点为一组进行实时干涉分析，待另撰文详述。

［1］SUN Yuwen，GUO Dongming.Iso－parametric tool path generation from triangular meshes for free － form surface machining［J］.The International Journal of Advanced Manufacturing Technology，2006，28:721 －726.

［2］CHRISTOPHE Tournier，EMMANUEL Duc.Iso－ scallop tool path generation in 5 － axis milling［J］.The International Journal of Advanced Manufacturing Technology，2005，25(9/10):867 －875.

［3］杨长祺，秦大同，石万凯.自由曲面五轴等残余高度高精度加工的路径规划［J］.计算机辅助设计与图形学学报，2003，15(5):621－626.

［4］杨旭静，杨钦文.基于离散刀位点的复合刀具路径生成方法研究［J］.湖南大学学报:自然科学版，2009，36(9):35 －39.

［5］康书杰，周来水，张绿礼，等.数控刀位点的B样条精确拟合［J］.机械工程与自动化，2007(141):95－97.

［6］赵艳春，张金萍，王丹，等.基于B3样条曲线的数控加工刀位轨迹计算的研究［J］.沈阳化工学院学报，2009，23(2):147 －149，169.

［7］陈晓兵，廖文和，吴海兵，等.三角网格表面数控加工圆弧样条刀轨研究［J］.中国机械工程，2009，20(14):1642 －1646.

［8］阳春启，杨旭静，王伏林.刀位点曲线拟合中的近似弧长参数化方法［J］.湖南大学学报:自然科学版，2008，35(8):34 －37.

［9］孟书云.高精度开放式数控系统复杂曲线曲面插补关键技术研究［D］.南京:南京航空航天大学，2006.

［10］刘根洪，何仁杰.微分几何与计算几何［M］.成都:四川大学出版社，2000:18－23.