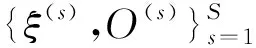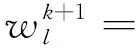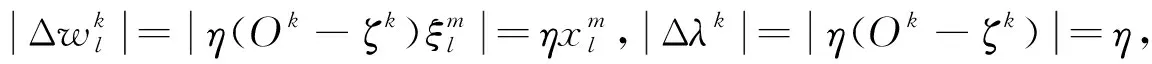带递归单元的模糊感知器的δ-规则的有限收敛性
2012-09-25刘燕,阎慧臻,刘超,姜行健,杨开兵
刘 燕, 阎 慧 臻, 刘 超, 姜 行 健, 杨 开 兵
( 1.大连工业大学 信息科学与工程学院, 辽宁 大连 116034; 2.大连理工大学 机械工程与材料能源学部, 辽宁 大连 16024 )
0 引 言
递归神经网络是指具有递归结构的神经网络,它们主要用来实现时间序列样本的分析及应用。网络结构分为全局递归连接和局部递归连接。全局递归神经网络结构复杂,难于训练和分析,在应用时需要将其结构简化。一种简单而自然的方法是对感知器引入反馈连接,其学习和训练依旧以前传为主,同时又包含反馈连接。这种网络的反馈使其输出不仅依赖当前的输入,还和上一时刻的输出有关,从而使网络具有动态记忆能力。
文献[1-3]对最简单的模糊神经网络即模糊感知器提出一种学习算法,并证明在一定条件下,该算法的有限收敛性。本文将对带递归单元的模糊感知器的学习算法收敛性问题进行研究。
1 带递归单元的模糊感知器网络结构及算法
1.1 带递归单元的模糊感知器结构

ζ(ξk)=g(max(W∘ξk,λ∧ζk-1))=
(1)
式(1)中,∨、∧分别为取大、取小运算,∘为合成算子,W=(w1,…,wn)T为权重向量,wj为连接第j个输入神经元和输出神经元的权值,连接递归神经元和输出神经元的权值为λ∈[0,1]。

图1 具有n-1-1结构的递归模糊感知器
1.2 完全随机输入的带递归的模糊δ-规则
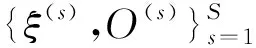
(2)
λk+1=f(λk+Δλk)=f(λk+η(Ok-ζk))
(3)
其中,l=1,…,n,k=0,1,…,且

2 样本模糊可分及样本集性质
为说明方便,记理想输出为O(s)=0和1的样本分别为Xm和Yp,m=1,…,M;p=1,…,P;1≤M,P 先定义两个集合:DM={1,…,M},DP={1,…,P}。 定义1若存在一个模糊向量A={a1,…,an},使得 (4) 成立,则称该训练样本模糊可分。 记模糊向量A中分量元素≥0.5的下标集合为E,分量元素<0.5的下标集合记为F,显然有E∪F={1,…,n}。 由假设1易得性质1~3[1]: 性质1E≠Φ且F≠Φ。 模糊感知器常用来解决分类问题,若理想输出等于实际输出则有限收敛,定义如下: (5) 成立,则称该学习算法有限收敛。 若σ2=0,任取η,则基于随机输入的带递归的模糊δ-规则有限收敛。 证明首先对学习算法作3点说明。 则max(Wk∘Yp,λk∧ζk-1)≥Wk∘Yp≥0.5 ζk=g(max(Wk∘Yp,λk∧ζk-1))=1=Ok 由算法(2)知 l=1,…,n λk+1=f(λk+η(Ok-ζk))= f(λk+η(1-1))=λk 由算法(2),当权值第k+1次被真正更新,则 λk+1=f(λk+η(Ok-ζk))=f(λk-η) (3)同说明(2)的推导,可得当λk∧ζk-1≥0.5,样本Xm,Φm=φ,m∈DM令权值严格减小;当λk∧ζk-1<0.5,对权值更新不起作用。 下面证明,权值有限次更新后达到收敛,并给出学习率η的选取范围。 对Xm,Φm=φ,m∈DM,易证ζ(Xm)=O(Xm)。综上,该学习算法收敛。 [1] YANG Jie, WU Wei, SHAO Zhi-qiong. A new training algorithm for a fuzzy perceptron and its convergence[J]. Lecture Notes in Computer Science, 2005, 3496:89-118. [2] 刘燕,杨洁. 带阈值的模糊感知器的收敛性[J]. 高等学校计算数学学校, 2005, 27(专辑):320-323. [3] 刘燕,阎慧臻,刘超. 利用模糊感知器解决模糊可分样本的分类问题[J]. 大连工业大学学报, 2009, 28(1):66-69. (LIU Yan, YAN Hui-zhen, LIU Chao. Classification of fuzzily separable training patterns based on fuzzy perceptron[J]. Journal of Dalian Polytechnic University, 2009, 28(1):66-69.) [4] WU Wei, SHAO Zhi-qiong. Convergence of online gradient methods for continuous perceptrons with linearly separable training patterns[J]. Applied Mathematics Letters, 2003, 16(7):999-1002.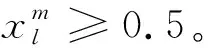


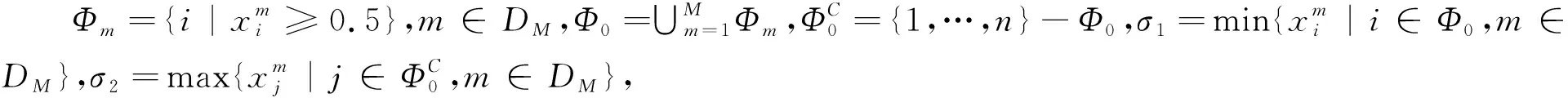


3 有限收敛定理及证明