基于出行时间预算负效用的出行行为建模＊

陈玲娟 刘海旭 蒲 云

（武汉科技大学汽车与交通工程学院1） 武汉 430081） （西南交通大学交通运输与物流学院2） 成都 610031）

出行者出行行为分析包括出发时刻选择和路径选择两个要素.van der Mede，Hu T.Y.等在交通分配模型里考虑了出发时刻的选择，但是模型没有考虑路网的不确定性，以及通勤者出行过程中的学习机制［1－2］.W.Y.Szeto等建立了动态交通分配下，同时选择路径和出发时刻的变分不等式模型（SRDTC）.该模型利用元胞传输模型来描述动态交通流状况，流量分配遵循动态用户最优和先进先出原则，并利用下降算法求解了模型［3］.H.F.Andy研究了带出发时刻选择的系统最优条件下的动态交通分配.并探讨了路网实现系统最优的必要条件［4］.Dick Ettema等将路网的不确定性描述为出行过程中路径走行时间的变化，建立了出行者对路网环境的学习机制，该学习机制强调感知不同出发时刻引起的出行时间均值和方差的变化［5］.Jou Rongchang等在出发时刻的选择中引入了前景理论的参考点假设，定义了2个参考点，可接受的最早到达时刻和最晚到达时刻，出行者根据出行过程中的损失和收益来调整下次出行的出发时刻［6］.本文基于出行时间预算［7］负效用的出行行为模型，假设同一个OD中具有相同风险偏好和相同上班时间的出行者选择相同的出发时刻，将其出发时刻的选择作为上层规划，路径选择作为下层规划建立了一个双层规划模型来描述其出行行为.

1 路径走行时间分布

1.1 路段走行时间分布

考虑路网G＝（N，A）.式中：N为节点集；A为路段集.R为起点r的集合，r∈R；S为讫点s的集合，s∈S；W 为 OD对w 的集合，w＝（r，s），w∈W；Pw为OD对w间所有路径p的集合，p∈Pw；Ta为路段走行时间变量；Ca为路段通行能力变量；va为路段a上的流量.

考虑到路网的不确定性，假设路段走行时间为一随机变量，采用正态分布函数来描述其概率分布.即Ta～N（E（Ta），V（Ta））.式中：E（Ta），V（Ta）分别代表变量Ta的均值和方差.

采用BPR函数来描述路段走行时间ta（va，ca）＝⎿1＋β（va／ca）n」，由于路段通行能力为变量，因此BPR函数写成变量的形式即为

由式（2）～（3）可知，要求得路段走行时间的分布函数，即要求得E（Ta），V（Ta），可以通过SP调查数据，进行数据拟合处理得到路段通行能力Ca的分布，求得E，进而得到路段走行时间的分布函数.

1.2 路径走行时间分布

路径走行时间与路段走行时间的关系可表示如下.

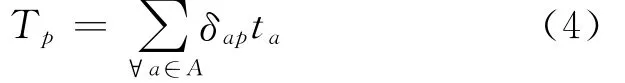
式中：δap为路段－路径关系变量，如果路段a属于路径p，则δap＝1，反之为0.

假设不同路段之间相互独立，由正态分布的可加性知，路段走行时间服从正态分布，则路径走行时间Tp亦服从正态分布，即

2 基于出行时间预算负效用的出行行为

路径选择与出发时刻选择是两个相互关联的问题，为了能在规定时间内到达目的地，出行者根据前次出行经验调整出发时刻，另一方面，确定了出发时刻，出行者选择不同的路径，使获得出行效用最大.出发时刻选择与出行时间预算的关系为tb＝T到－T出，其中tb为出行时间预算，T到为必须到达的时刻，T出为选择的出发时刻.因此，出行行为也是一个同时确定出行时间预算和选择路径的行为.

2.1 出行时间预算的选择

出行者在进行出行时间预算选择时，在可接受的出行费用范围内，使得准点到达的概率最大，即 max Z＝p（tb－te≤tp≤tb＋tl） （6）式中：tb为出行者出行时间预算；te为允许早到时间；tl为允许迟到时间，即实际路径走行时间tp∈（tb－te，tb＋tl）时，均看作准点到达.

式中：E（Ta），V（Ta）为路段流量的函数.因此，Z为路段流量的函数.

2.2 基于出行时间预算负效用的路径选择

2.2.1 出行时间预算负效用的概念

路径走行时间Tp～N（E（Tp），V（Tp）），出行时间预算和出行费用（包括迟到费用，早到费用和走行费用）与路径走行时间的关系见图1.

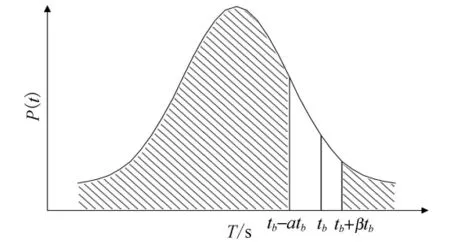
图1 路径走行时间分布

图1 中左边阴影部分代表出行时间预算确定情况下早到的概率，右边部分代表迟到的概率，中间空白部分tp∈（tb－te，tb＋tl）为准点到达概率.路径p的期望总出行费用fp表示如下.

式中：fe（t）为早到产生的期望费用；fl（t）为迟到产生的期望费用；f（t）为整个过程中走行产生的期望费用.

设早到t min产生的费用函数为Fe（t），迟到t min产生的费用函数为Fl（t），走行t min产生的费用函数为F（t），一般情况下有：Fe（t）≤F（t）≤Fl（t），p（t）为路径走行时间分布函数.

根据图1的概率分布可得

路径的出行时间预算负效用Up与费用fp满足关系U＝－f，θ为校正参数.

2.2.2 路径选择的logit模型

出行者在进行路径选择时，使得路径的出行时间预算负效用Up最大，即使得路径期望总出行费用fp最小.假设出行者对于出行总费用的理解存在误差，即出行者感知到的路径实际出行费用为式中：εp为出行者对路网信息的感知误差，假设其服从Gumble分布.

根据效用最大化理论，路径p的选择概率Pp为

3 模型及求解算法

3.1 出行行为的双层规划模型

根据上述分析，可以建立基于出行时间预算的出行行为双层规划模型，将出行时间预算tb的确定作为上层决策，下层模型为tb确定下的路径选择模型，具体模型如下.

上层模型

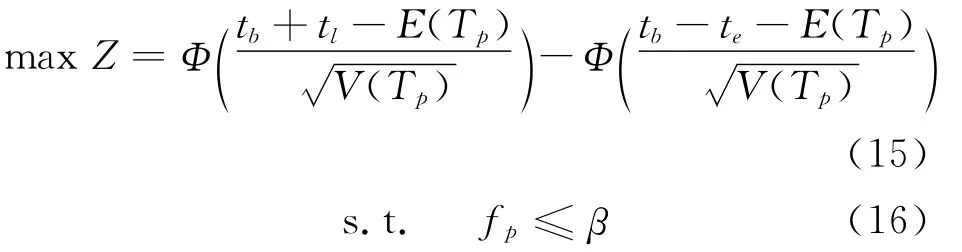
式中：β为出行者对出行费用的最大限额.

在出行时间预算确定下，路网流量q是出行费用f的函数，f是路径走行时间t的函数，t是路径流量q的函数，由此得到等价于式（14）的不动点形式的分配模型如下［9］：

式中：Q，F，T分别为q与f，f与t，t与q之间的函数关系.

3.2 基于路径的下层模型求解

下层模型的求解是在已知路段通行能力分布的条件下，对给定的tb在OD对间进行流量分配.由于出行费用的计算需要列出路径流量，利用相继平均法（MSA），结合logit配流方法给出下层模型的求解［10］，具体算法步骤如下.（1）初始化.令k＝0，定义网络中所有OD对的可能路径.找到一个路径流量的初始可行解，根据路段路径关系得到路段流量的可行解；（2）期望出行费用计算.迭代进行到第k（k＝1，2，…）步，利用式（2）～（5）计算每条路径的走行时间分布.再利用式（6）～（9）计算每条路径的期望费用；（3）寻找下降方向.将出行需求q按式（11）进行流量的加载，得到所有可能路径的流量；（4）更新.令＝＋－），根据路段路径关系得到路段流量vka＋1；（5）终止条件.当迭代进行到指定次数，则终止；否则令k：＝k＋1，重复（2）～（4）.

3.3 基于遗传算法的双层规划求解

本文采用遗传算法来求解整个双层规划，个体的适应度值Z由式（15）得到，式（15）中E（Tp），V（Tp）为路段流量va的函数，va由求解下层规划得到.具体算法步骤如下.

1）初始化 （1）采用二进制编码来表示参数，根据求解精度要求，设置染色体长度，给出编码解码方法；（2）设置群体大小，生成初始种群；（3）设定交叉概率和变异概率的值.

2）求解个体适应度值 将染色体串解码，转化成实际值（即tb）.求解下层规划得到va，代入式（2）～（5）得到E（Tp），V（Tp），代入式（12）得到适应度值.

3）遗传操作 （1）利用轮盘选择算子进行选择运算；（2）利用单点交叉算子，根据设定的交叉概率，对父辈染色体进行交叉运算；（3）根据设定的变异概率进行变异运算.

4）终止条件 当迭代进行到指定次数，则终止；否则重复2）～3）.

4 算 例

构造一个简单例子来验证模型和算法的有效性.如图2所示，该网络包含一个从①到④的OD对，4个节点，5条路段，其中路段3为单向路段，考虑该OD对中仅包含出发时刻相同的出行者.

图2 例子网络

路段走行时间采用BPR函数，Ta（va）＝ta0［1＋0.15（va／ca）］4，t为路段的自由走行时间.OD对需求为qw＝60.路段通行能力Ca呈现均匀分布，最小通行能力为pa.其中路段设计通行能力.费用函数Fe（t）＝0.5t，Fl（t）＝t2，F（t）＝t，te＝0.1tb，tl＝0.05tb，出行费用的最大限额β＝10，校正参数θ＝0.01.其余各参数的取值见表1.

表1 网络参数

设置遗传算法的群体包含20个个体，采用二进制编码，交叉概率pc＝0.7，变异概率pm＝0.3，循环终止次数为50次.个体适应值由式（15）得到，MSA算法循环终止次数为40次.计算结果见表2.

表2 计算结果

5 结束语

在随机路网中，路段通行能力，路径走行时间都具有不确定性，出行者要综合考虑出发时刻选择和路径选择.通勤者选择出发时刻，确定出行时间预算，再根据路径出行时间预算负效用选择路径出行，并利用此次出行信息来调整下次出行的出发时刻，经过多次出行达到稳定状态.本文提出了出行时间预算负效用的概念，建立了与logit选择概率等价的不动点模型，用双层规划描述了出发时刻选择和路径选择之间的关系.用MSA算法求解下层配流模型，并用遗传算法求解了整体双层规划模型.算例部分假设OD对中仅包含出发时刻相同的出行者，在实际应用中，将同类型的出行者在路网上加载时，应考虑路网中已存在的流量，且出发时刻不同，面临的路网流量不同.因此，在进一步的研究中，应考虑出发时刻与路网已存在流量之间的动态关系，确定流量加载时路网中已存在的流量.

［1］van BERKUM.The impact of traffic information：dynamics in route and departure time choice［D］.Delft：Delft University of Technology，1993.

［2］HU T Y，MAHMASSANI H S.Day－to－day evolution of network flows under real－time information and reactive signal control［J］.TransporTation Research C，1997，5（1）：51－69.

［3］SZETO W Y，HONG K.A cell－based simultaneous route and departure time choice model with elastic demand［J］Transportation Research Part B，2004，38（7）：593－612.

［4］ANDY H F.Properties of system optimal traffic assignment with departure time choice and its solution method［J］.Transportation Research Part B，2009，43（3）：325－344.

［5］ETTEMA D，TAMMINGA G，TIMMERMANS H，et al.A micro－simulation model system of departure time using aperception updating model under travel time uncertainty［J］.Transportation Research Part A，2005，39（4）：325－344.

［6］JOU Rongchang，KIRAMURA R，WENG Meichuan，et al.Dynamic commuter departure time choice under uncertainty［J］.Transportation Research Part A，2008，42（5）：774－783.

［7］HONG K，LUO X W，BARBARA W Y.Degradable transport network：Travel time budget of travelers with heterogeneous risk aversion［J］.Transportation Research Part B，2006，40（9）：792－806.

［8］HONG K，TUNG Yeoukoung.Network with degradable links：capacity analysis and design［J］.Transportation Research Part B，2003，37（4）：345－363.

［9］范文博，李志纯，蒋葛夫.基于参考依赖法的出行者日常路径选择行为建模［J］.交通运输工程学报，2009，9（1）：96－99.

［10］TVERSKY A，KAHNEMAN D.Loss aversion in riskless choice：a reference－dependent model［J］.Quarterly Journal of Economics，1991，106（4）：1039－1061.