交通信息系统在高峰期事故瓶颈中影响作用分析＊

张 邻 杜 文

（南昌航空大学数学与信息科学学院1） 南昌 330063）（西南交通大学交通运输学院2） 成都 610031）

在近10年许多学者对旅行者信息系统的各个方面进行了广泛的研究，但这些研究大都假设或隐含旅行者都遵从交通信息系统的诱导，没有把旅行者的行为决策体现在模型中［1］.还有一些理论研究是以驾驶者部分遵从交通信息系统的诱导为前提，并且假定路网中驾驶员的遵从诱导的比例是固定的［2］，或者按照一定的规律变化［3］，以便研究交通信息系统的实施效用.另外，一些学者从实证的角度进行研究，试图解释驾驶者部分遵从交通信息系统的比例范围［4－6］.本文在一些假设的前提下论证了交通信息系统的利益，研究焦点是驾驶者的路线决策，分析和评估交通信息系统对交通状态的影响结果，并结合实例分析对驾驶员诱导的最终结果.

1 交通走廊高峰期的通行分析

如图1所示，为了便于对事故的瓶颈进行理解和分析，令在单个OD对起点A和终点D之间有2条路线ABFCD和路线ABECD，假设路线ABFCD是一条快速路，路段BEC是一条普通等级的公路.路段BFC的长度为l1，路段AB，BFC和CD的容量都为c1且路段AB，BFC和CD 的自由流速度都为v1，路段BEC的长度为l2，容量为c2，自由流速度为v2，且v1＞v2，l1＜l2，c1＞c2.令路段AB的流量为q，路段BFC的流量为q1，路段BEC的流量为q2，且路段BFC的流量和路段BEC的流量为路段AB的流量分流得到的，即q＝q1＋q2.

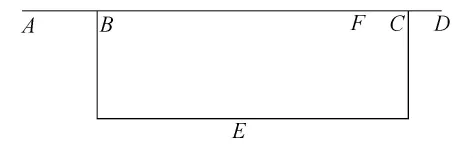
图1 交通走廊

假设，从起点A出发的车辆到达B点后将根据路段BFC和路段BEC的行驶时间、流量和容量来选择路径.根据已知条件，在路段BFC是自由流的情形下，到达B点的车辆将全部选择路段BFC，即q1＝q且q2＝0.设路段AB在非高峰期始终以自由流行驶，且在高峰期流量不超过容量.在高峰前的某时刻流量以变化率r增加，不妨假定为0时刻，随着时间的增大，流量变化率不断减小，直到T时刻流量达最大值，这时流量变化率为0，随后流量以对称于0～T时段变化率逐渐减小，到2T时刻流量恢复正常值q，即T～2T时段流量变化率，由0逐渐变化到r.设在0时刻，路段BFC流量以变化率r1增加，且路段BEC流量以变化率r2增加.对于路段BFC来说，在0～T时段，随着流量的增加，由于受到容量的限制，容量对流量变化率的阻滞作用越来越大，因此，路段BFC流量的变化率r1是流量q1的函数，即r1（q1）.设r1（q1）与q1成正比例关系，即r1（q1）＝r1－aq1.其中：a是比例系数.当q1＝c1时，路段BFC的流量将不再增长，即r1（c1）＝0，得a＝r1／c1，因此，r1（q1）＝r1（1－q1／c1），其中因子（1－q1／c1）可以理解为路段BFC的流量对增长率r1的阻滞作用.同时，由于存在路段BEC的分流作用，同样对路段BFC的流量增长率r1也有一定的阻滞作用，也就是说，在阻滞因子（1－q1／c1）中再减去一项，该项与q2成正比（相对于c2），因此，路段BFC流量的增长率修正为

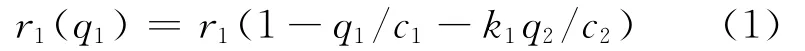
同理可得，对∀t∈［0，T］，路段BEC的流量变化方程为˙q2（t）＝r2（1－w2q2）q2.式中：w2＝.令路段BEC流量在0时刻的初始值为q2（0）＝q02，解微分方程得t∈［0，T］时刻流量变化方程为

同理得0～α时间段（0≤α≤T）通过路段BEC上某点的车辆数为接下来根据上面的模型来讨论在高峰期交通瓶颈处的交通阻塞情况.

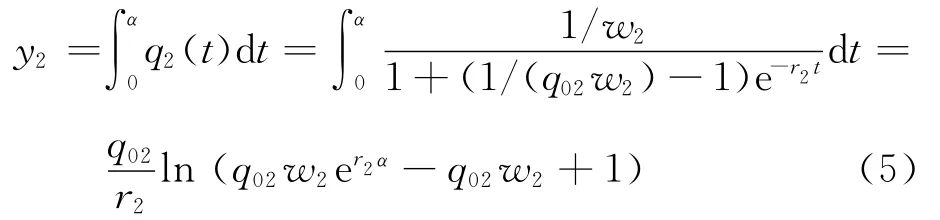
2 在高峰期发生交通事故时交通走廊的车辆通行分析

2.1 所有车辆都没有安装交通信息系统

假定路网中所有车辆都没有安装交通信息系统.对于路段BFC来说：若a＋T′≤T.令t∈［a，a＋T′］，则在［a，t］时段通过事故点的车辆数为

式中：t－a≤T′.由于是4车道，排队等待的车辆为2列，令x1是排队等待的车辆数，则排队等待所占用的道路长度为l′＝·b＝x1b.令l0

为驾驶员能观测到前面车辆的最大距离，则当L－l′＞l0时，由式（2）、（3）和（6），在［a，t］时间段排队等待的车辆数为

式中：t－a≤T′.当0≤L－l′≤l0时，到达B点的车辆观测到路段BFC排队等待的队尾，驾驶员在B点将根据自己的行为模式改变车道，大部分驾驶员将选择道路BEC，这样道路BFC上的车辆增长率变小，不妨设为r′1，并且道路BFC上排列等待的车辆队列长度l′始终保持0≤L－l′≤l0，直至事故处理完毕.不妨假设排队占用道路长l′＝L－l0保持不变，事故道路排队等待的车辆数保持动态平衡，即道路BFC上排队等待的车辆数保持不变.同时道路BEC的增长率变大，不妨设为r′2.

若T＜a＋T′≤2T.当L－l′＞l0时，由于前面假设0～T时间段路段BEC上车辆增长率与T～2T时间段到达减少率是对称的，令t∈［T，a＋T′］，根据对称性，由式（2），在［T，t］时段排队的车辆数为－∫Ttq1（t）dt，这里T≤t≤a＋T′≤2T，由式（2），（3）和（6），在［a，t］时段排队的车辆数为

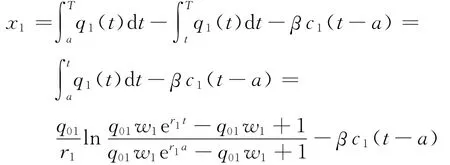
同理，当0≤L－l′≤l0时，假设排队长l′＝L－l0保持不变，即道路BFC上排队等待的车辆数x1保持不变.

对于路段BEC来说：在不知道前方道路发生事故的情形下，驾驶员在B点基本选择道路BFC，所以t0时刻前，道路BEC的车流量小于它的容量.由式（4）和（5），在t∈［a，t0］时段通过路段BEC的车辆数为

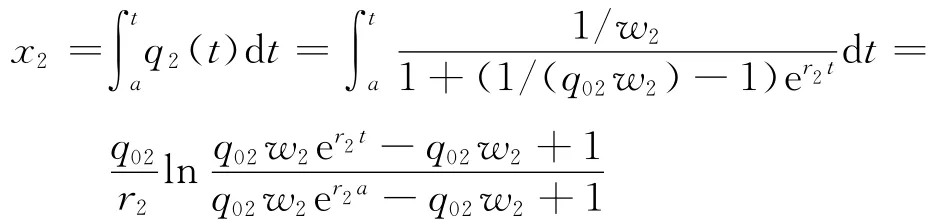
设t1为道路BEC上的车流量恰好达到道路容量那一刻，令t1∈［t0，a＋T′］，这时q2（t1）＝c2，［t0，t1］时段变化率变为r′2，t0时刻的流量q2（t0）变为初始流量，不妨令t0时刻为时刻0，则对∀t∈［t0，t1］，由式（4）和（5），在［t0，t］时段通过的车辆数为

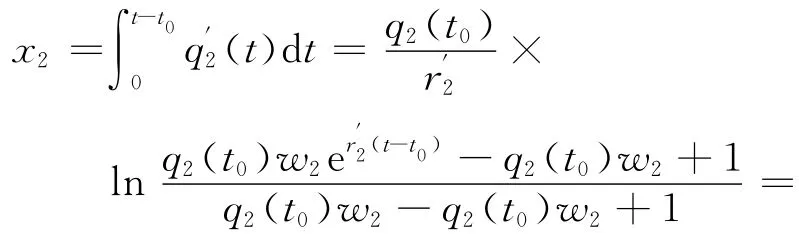
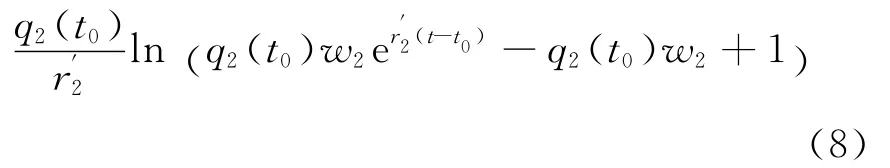
在［t1，a＋T′］时段，由于在［t0，a＋T′］时段，路段BEC的流量不断增加，那么在t1时刻后，将在路段BEC上形成堵塞，而在［t0，a＋T′］时段，路段BFC的排队队长始终保持0≤L－l′≤l0，所以交通事故所引起的排队等待队列将延伸到路段AB上，从而整个网络都陷入严重阻塞情形.

综上所述，事故期间道路BEC通过的车辆数为

2.2 部分车辆安装交通信息系统

若该OD对中有部分车辆安装有播报路网实时交通状况的信息系统，那么安装有交通信息系统的车辆，从事故发生时刻a起，在决策点B根据自己的行为模式进行道路选择.若安装有交通信息系统的车辆的比例为γ，从a时刻起，装有信息系统的车辆将有很大比例的车辆转道BEC，使路段BEC上的车辆增长率将增加到r″2，路段BFC上的车辆增长率减小到r″1.

对于道路BFC来说，由于时刻a之前的道路BFC上的流量小于c1，因此，由式（2），a时刻的流量为q1（a），令t∈［a，a＋T′］，则在［a，t］时间段内，由式（3）、（6）和（8）得路段BFC上排队车辆数为

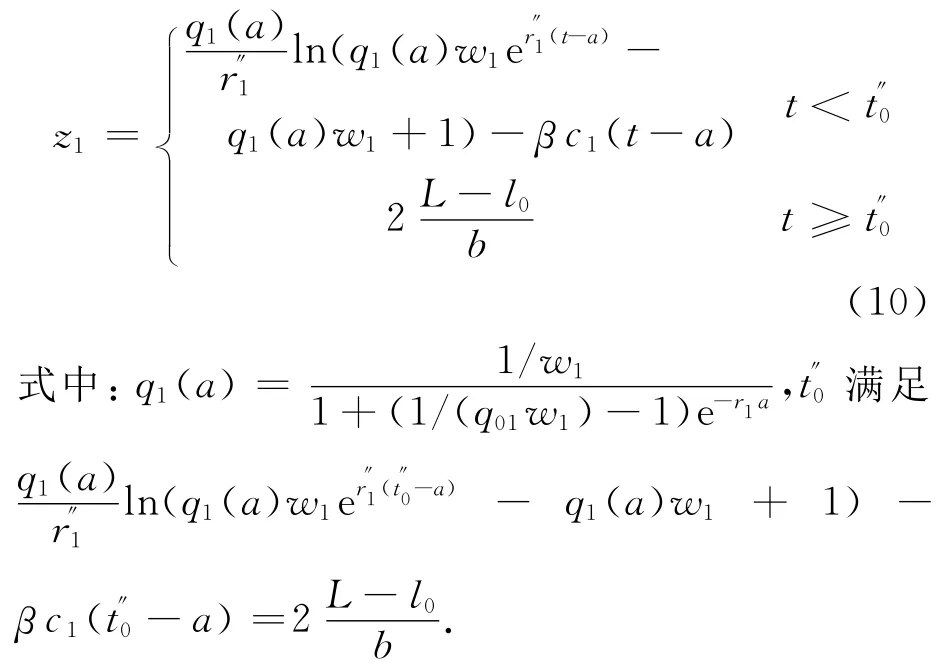
对于路段BEC来说，在a时刻路段流量为q2（a），并以增长率r″2增长，则当t∈［a，t″0］时，由式（8）得，路段BEC在a～t时段通过的车辆数

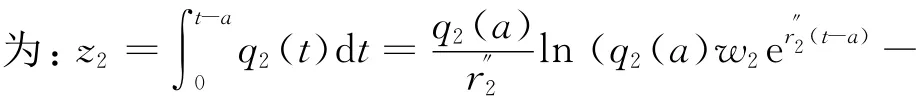
q2（a）w2＋1）.当流量增加到时刻t″0以后，由于路段BFC上排队等待的车流尾部在B点可以看得见，没有安装交通信息系统的很多车辆进入路段BEC，从而路段BEC 增长率增长到r，即在t时刻，路段BEC 流量为q2），并以变化率r增长.令t∈］，由式（8），道路BEC事故期间通过的车辆数，即道路BEC 在时间段［a，t″0］和时间段，t］通过车辆数总和为

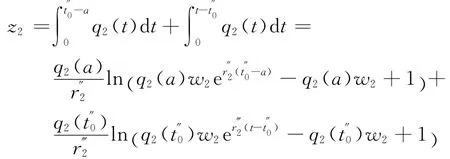
随着道路BEC的流量的不断增加，同样存在时刻t′1，道路BEC流量恰好达到道路BEC的容量.

综上所述，事故期间道路BEC通过的车辆数为

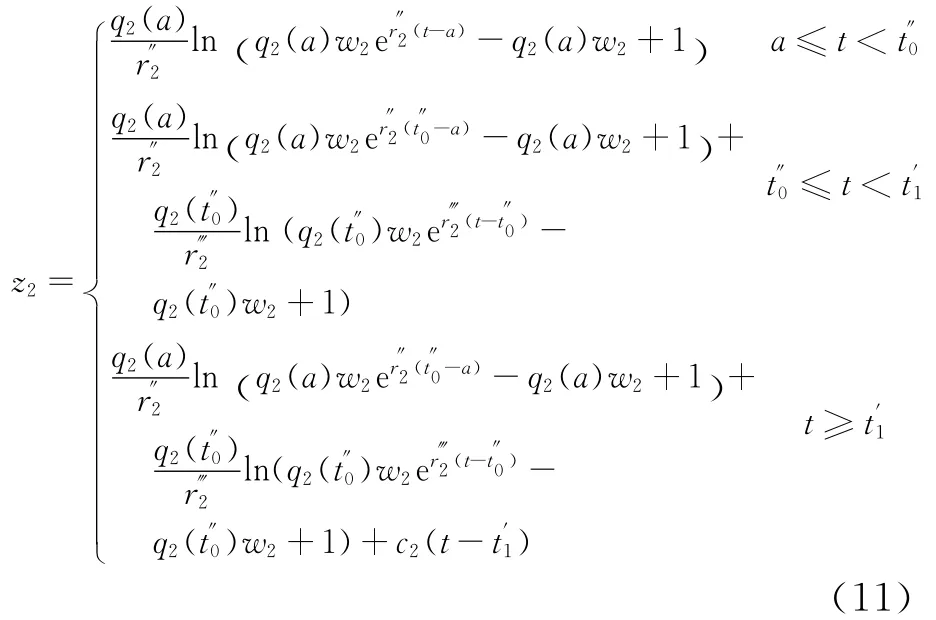
式中：

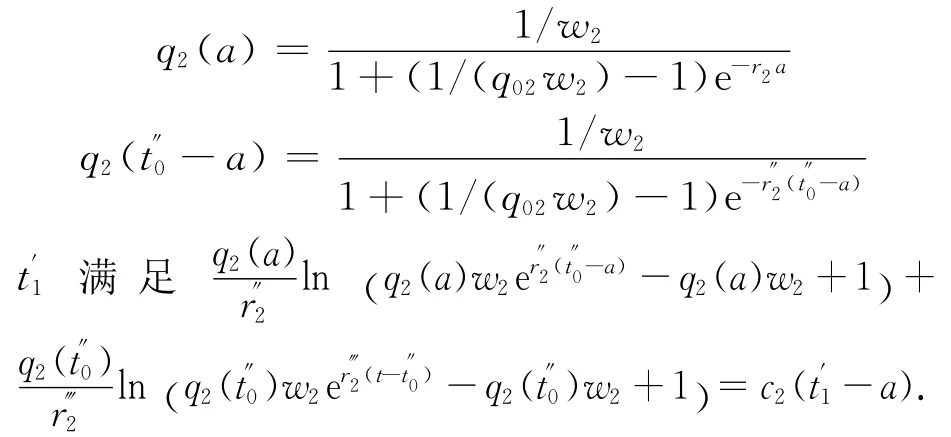
3 例 证

南昌市老福山D与南昌县A之间有两条路线，一条是由南莲塘路AB，经井冈大道BFD到达；另一条是可有南莲塘路AB，经迎宾大道BED绕行到达（见图2）.井冈大道BFD长l1＝12km，自由流速度v1＝48km／h，道路容量c1＝7 980veh／h，初始流量q01＝2 660veh／h，莲塘路早高峰期初始车流增长率r＝2.4min，井冈大道早高峰期初始车流增长率r1＝2.1min，井冈大道BFD路段容量在交通事故后是原来容量的β＝1／3，高峰时间2T＝60 min，事故处理时间T′＝30min，F点在时刻a＝5min发生交通事故，BF的长L＝10km，排队平均车间距b＝6m，目视距离l0＝300m，路网中装有能够播报实时路况信息装置的车辆比例γ＝3／4，迎宾大道BED长度l2＝15km，自由流v2＝30km／h，道路容量c2＝3 990veh／h，初始流量q02＝3veh／h，高峰期0时刻车流增长率r2＝6min.

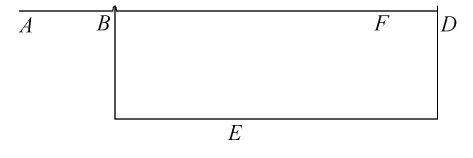
图2 南昌市井冈大道和迎宾大道

利用式（7）和式（10）分别对路网中部分车辆安装电子装置和全部车辆都没有安装电子装置的情形进行模拟，得事故处理时间与阻塞车辆占用道路长度之间的关系，见图3.

图3 阻塞车辆占用道路长度与事故处理时间之间关系

由图可以看出，对于井冈大道BFD来说，在0～5时刻，流量小于容量，没有车辆阻塞，在时刻5发生交通事故后，有、无电子装置2种情况，阻塞车辆占用道路长度都与事故处理时间成正比，且无电子装置斜率比有3／4车辆安装电子装置斜率大，即阻塞车辆占用车道长度的增长速度是有电子装置情形下的2倍多.在事故处理结束时，全部无电子装置车辆占用车道长度约为7km，有3／4车辆安装电子装置情形下，阻塞车辆占用车道长度约为2km.对于迎宾大道BED来说，在无电子装置情形下，由式（9），事故期间通过车辆数为665，车辆有3／4比例安装电子情形下，由式（11），事故期间通过的车辆数为1 998.这与该事故所引起的井冈大道阻塞队长约3km和迎宾大道车流量达到饱和的情形基本一致.

4 结束语

车辆配备交通信息系统降低了网络中车辆的平均延误，增加了网络效用.路径选择分配模型表明，在前方发生交通事故的情形下，随着配备信息系统车辆比例的增加，网络中车辆平均旅行时间总体趋势是减少的，这是因为信息系统使人们较早转变车道，使得网络更接近系统最优均衡.总的来说，长的事故处理时间引起高的交通需求率，在路网有足够替代路线的能力前提下，对车辆积极引导向最小化行车时间的路线能产生显著系统效益.最后，在较大规模的网络中研究和验证车辆配备信息系统的效用有待将来进一步研究.

［1］ERICSSON E，LARSSON H，FREIJ B K.Optimizing route choice for lowest fuel consumption－potential effects of a new driver support tool［J］.Transportation Research Part C，2006，14：369－383.

［2］ MAMMAR S，MESSMER A，JENSEN P，et al.Automatic control of variable message signs in aalborg［J］.Transportation Research Part C，1996，4（3）：131－150.

［3］DEFLORIO F P.Evaluation of a reactive dynamic route guidance strategy［J］.Transportation Research Part C，2003，11：375－388.

［4］ERKE A，SAGBERG F，HAGMAN R.Effects of route guidance variable message signs （VMS）on driver behavior［J］.Transportation Research Part F，2007，10（6）：447－457.

［5］HAITHAM M，DEEK A L，KHATTAK A J，et al.A combined traveler behavior and system performance model with advanced traveler information systems［J］.Transportation Research Record，1998，32（7）：479－493.

［6］李文勇，陈学武，陈 峻.交通出行诱导的Stackelberg博弈模型及其遗传算法求解［J］.武汉理工大学学报：交通科学与工程版，2009，33（5），983－987.