声辐射阻抗传感器的原理设计与标定方法研究＊

向 阳 郭志勇 王校清

（武汉理工大学能源与动力工程学院 武汉 430063）

有限元＋边界元法是目前结构辐射噪声预估中最常用的方法，但边界元法存在奇异积分的处理，计算近边界声场时数值解很不稳定乃至严重失真，波叠加法是改进这一问题的方法之一.用波叠加法求取结构辐射声功率时，要用到结构的辐射阻抗矩阵，在安静结构设计中常用附加点质量的方法改变结构的辐射声功率，其实质就是改变了结构本身的辐射阻抗矩阵，由此可见结构的辐射阻抗矩阵在安静结构设计中是十分重要的设计变量.结构的辐射阻抗矩阵可以通过解析法或数值计算的方法来求解，但这种方法对规则形状的结构比较适合，而结构形状复杂时，这种方法就不再适用.因此，本文研究用实验法测定结构的声辐射阻抗，实验测定不受结构几何形状的制约，同时测定的声阻抗在一定频率范围内可具有较高的精度［1］，可作为解析法或数值法的补充方法，用于工程实践中的安静结构设计.

1 声阻抗计算公式的导出

由波叠加法［2－3］可知，结构的辐射阻抗矩阵中任意一元素即任意2点间的声阻抗Za，ik定义为

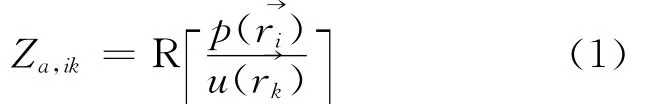
另外，实验时用来模拟点声源的扬声器要用密封圈进行密封，保证其在工作时近似为一个点声源.否则扬声器的两边都将进行声辐射，此时扬声器更接近为一个偶极声源，而不是一个点声源，而偶极声源在低频时的辐射效率是很低的［4－5］.小声源的平均辐射声功率近似公式为

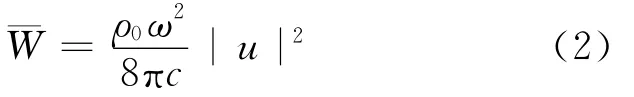
式中：ρ0为介质的密度；c为声速；ω为圆频率（2πf）；u为声源的体积速度.由式（2）可知，低频时所辐射的能量较低.

由声学理论可知，小体积腔室内部声压大小取决于腔室内做简谐振动的壁面振速大小，用公式可表示为［6］

式中：u为腔室振动壁面的振动体积速度，见图1a）；V为腔室的体积.

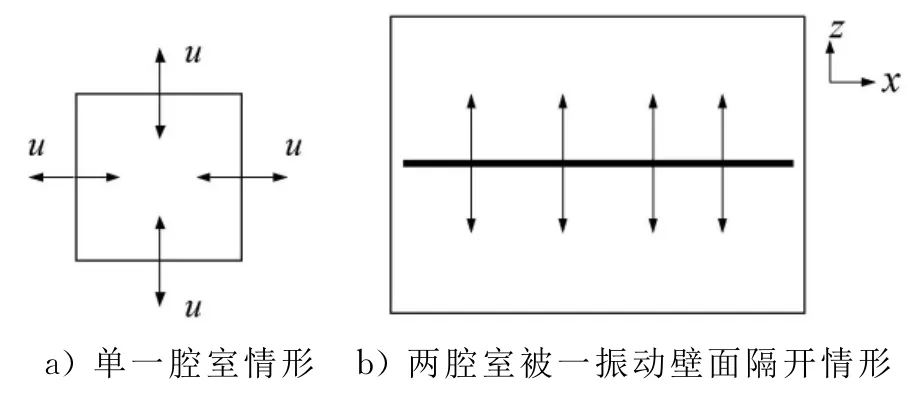
图1 确定腔室内声压示意图

分析时忽略腔室内驻波的影响，同时认为腔室的体积V为已知，且腔内感知声压的麦克风没有相位误差，那么，通过测量扬声器内的声压就能用式（3）计算其振动体积速度.但是，实际使用的扬声器的形状是十分不规则的，其腔室的体积不易准确得到，此外，麦克风的相位误差也是不能忽略的.因此，必须对声阻抗测量装置进行必要的校准，校准时需要在实验用扬声器上面设置一个已知体积的腔室（校准腔V2）.图1b）为校准腔的示意图，用式（3）可以得到2个腔室的声压比，即

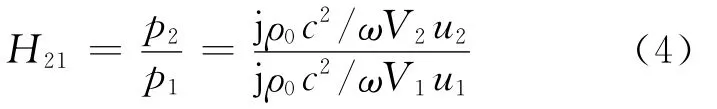
可以证明式（4）中体积速度u1和体积速度u2大小相等、方向相反.所以，式（4）可以化简为

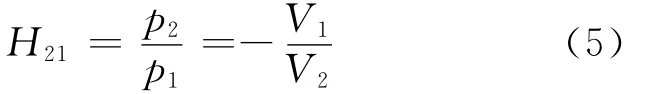
由式（5）可知，要想确定扬声器腔室V1的体积，只需同时测量2个腔室内的声压即可.

假设腔室2的直径为d，沿x方向的长为l，且声波以平面波的形式在其内传播，则根据式（6）可以计算得到沿腔室轴向上（z方向）的声压大小.

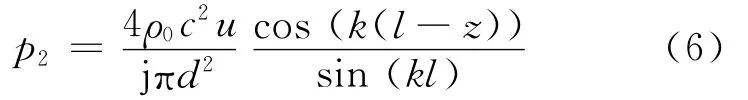
此时，只需测量腔室2顶部的声压（z＝l），腔室2的体积由V2＝πld2／4计算得到，则式（6）可以化简为

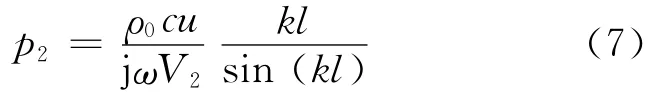
若用Vs和Vc分别代表声源腔体积和校准腔的体积，ps为声源腔内的声压.由式（3）可得

将V1和V2分别用Vs和Vc代替后代入式（5），可得

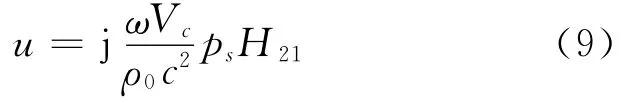
通过式（9）可以获得结构表面任意一点k处的体积速度为

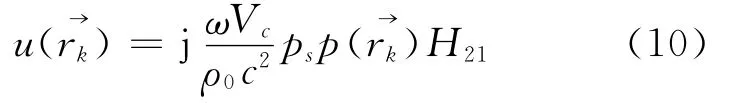
此时，只要再测量出结构表面任意一点i的声压，就可以由式（10）得到任意2点间的声阻抗Za，ik

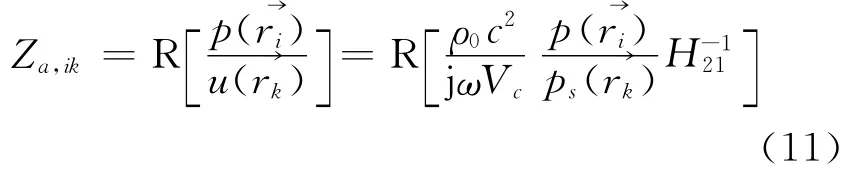
式中：i＝k时为自阻抗，i≠k时为互阻抗.

进一步化简可得

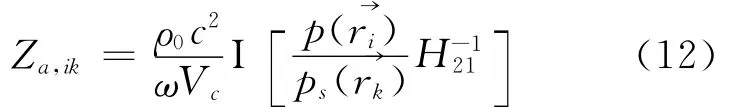
先通过校准实验获取H2－11就可以修正麦克风之间的相位不同，再通过所设计的测量装置，逐点测量结构表面声压和声源腔的声压就可用式（12）计算得到任意2点间的声阻抗Rik.

2 校准腔的设计

根据上节所述校准原理，设计的校准腔见图2.实验时将图2下部装有扬声器的声源腔嵌入图2上部的校准腔，扬声器同时激励校准腔和声源腔，校准腔的声压由安装在其顶部的麦克风测量，校准腔顶部安装麦克风处和下部嵌入扬声器处均需密封，校准腔的轴向长度l的设计准则是使其中的声压级变化不超过1dB.

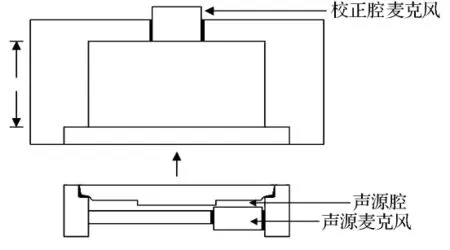
图2 设计的校准腔示意图

3 校准实验

校准实验系统见图3.设备包括扬声器1只、全指向性麦克风2只、NI9234采集模块、NI9263电压输出模块和cDAQ数据采集器，所选设备的性能指标见表1.

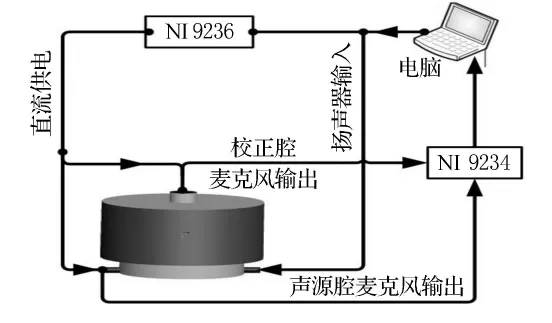
图3 校准实验系统图

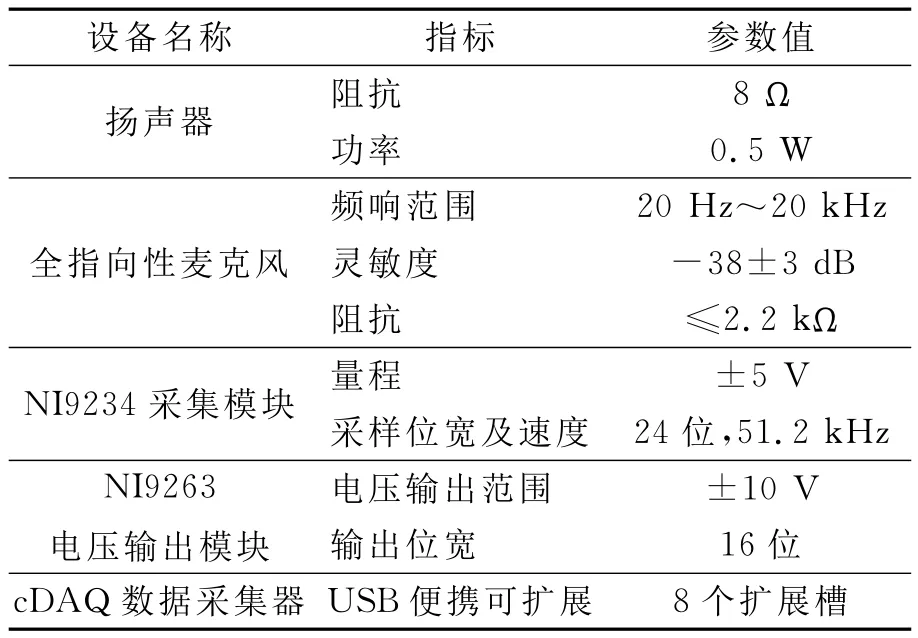
表1 主要设备性能参数

校准实验在消声室中进行，实验装置及测试系统见图4.

图4 校准实验

实验采用单频正弦信号进行激励，正弦信号的频率范围为200～3 100Hz，每间隔10Hz测量一次.将测量的数据进行信号处理后得到每个单频点处H21的值，最后由这些单频点处的H21值绘制其随频率变化的曲线.图5～12为激励频率分别为600Hz和2 600Hz时，信号滤波前后的对比.

图5 600时采集到的校正腔信号

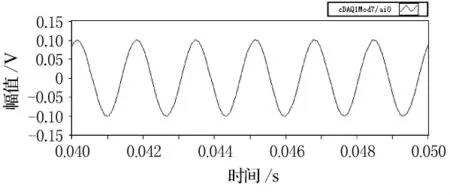
图6 滤波后600Hz校正腔信号

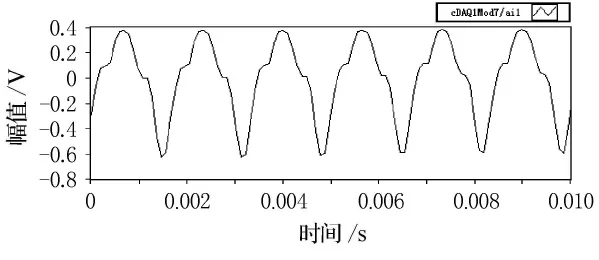
图7 600Hz时采集到的声源腔信号

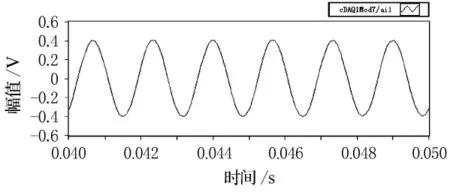
图8 滤波后600Hz声源腔信号

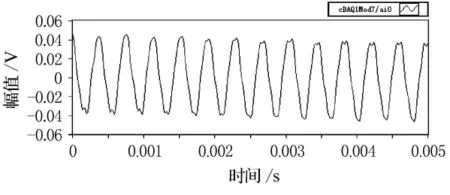
图9 2 600Hz时采集到的校正腔信号

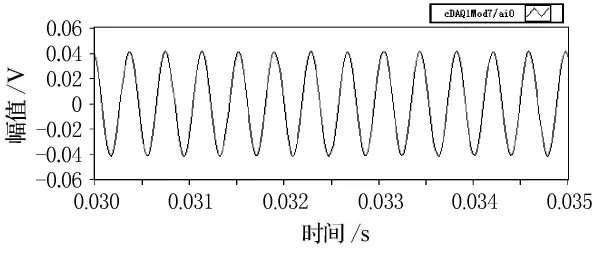
图10 滤波后2 600Hz校正腔信号

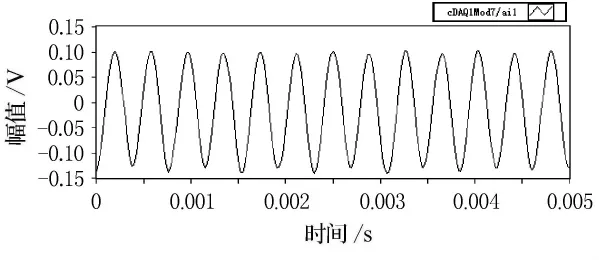
图11 2 600Hz时采集到的声源腔信号

由图5～12的比较可以看出，扬声器发出的单频激励在较低频率时（600Hz），麦克风接收后产生较大的畸变，这主要是由于扬声器在低频时辐射声波的能力不强造成的，但经过滤波处理后，能较好的还原单频正弦信号.随着激励频率的逐渐升高（2 600Hz），麦克风采集的信号畸变也逐渐减小，滤波前后波形的形状变化不大.

将所有采集的单频信号数据都进行上面的滤波处理后，再通过加窗，FFT变换，最终可以得到每个采样频率点处的H21.图13～16为1 600Hz处声源腔和校准腔信号的频谱实部、虚部，对比图13和图14以及对比图15和图16能够发现，校正腔和声源腔信号的相位正好相反，这与第一节中分析结论一致.图17为最终所得的标定曲线H21.

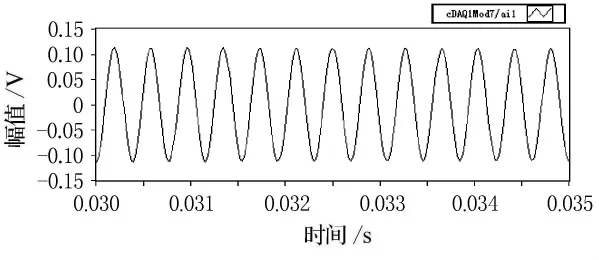
图12 滤波后2 600Hz声源腔信号

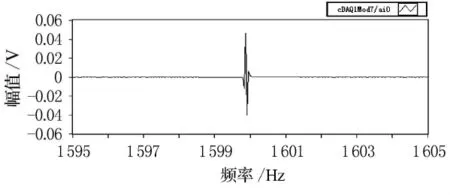
图13 校正腔信号频谱实部

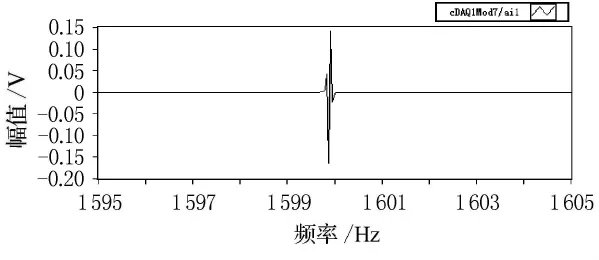
图14 点声源腔信号频谱实部

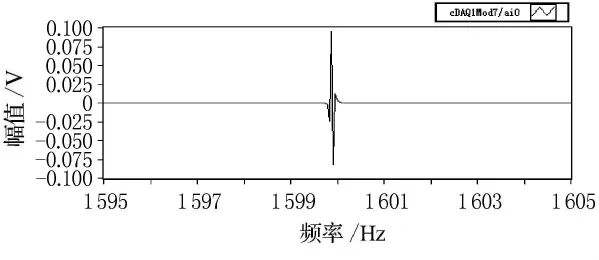
图15 校正腔信号频谱虚部

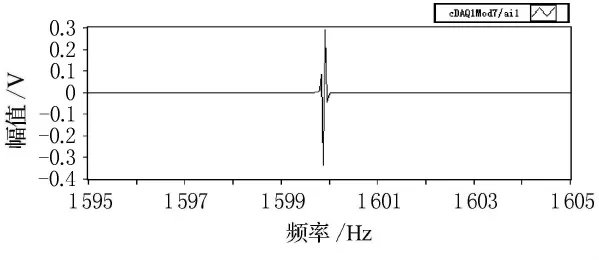
图16 点声源腔信号频谱虚部

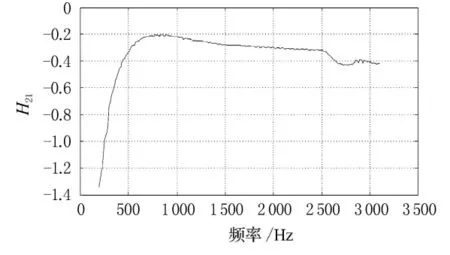
图17 实验得到的H21曲线

由图17可以看出，在实际测量中2麦克风之间的相位关系并非固定不变，而是随频率变化而变化的.在低频段两麦克风之间的相位随频率变化较大；在中间频段时两者的关系较为稳定；在高频时两者的关系也有一些波动，但变化不是十分剧烈.

4 结束语

研究了实验测定声阻抗的理论计算公式，然后根据声学理论设计出实验用的点声源腔和校正腔，选取了合适的扬声器、麦克风、信号采集设备并搭建了实验系统.并根据标定实验所获得的数据，通过信号后处理，最终得出两麦克风之间的相位－频率关系曲线.该校准曲线在后续的声阻抗测量实验研究中，将代入式（12）中用于声阻抗的实际计算.

［1］KOOPMANN G H，FAHNLINE J B.Designing quiet structures［M］.San Diego：Academic Press，1997.

［2］向 阳，GARY H，KOOPMANN G H.基于波叠加原理的辐射声场的计算研究［J］.武汉理工大学学报：交通科学与工程版，2005，29（1）：1－4.

［3］向 阳，郭志勇.波叠加法在结构辐射声功率计算中的应用［J］.应用声学，2010，29（1）：48－52.

［4］JORGE P，ARENAS A.Analysis of the acoustic radiation resistance matrix and its applications to vibroacoustic problems［D］.Auburn：Auburn University，2001.

［5］马大猷.现代声学基础［M］.北京：科学出版社，2004.

［6］BERANEK.Acoustics［M］.New York：Acoustical Society of America，1986.