侧向风荷载对人－车－路系统耦合振动的影响分析

张丙强 李 亮

（福建工程学院土木工程系1） 福州 350108） （中南大学土木建筑学院2） 长沙 410075）

车辆与路面的耦合振动和车辆乘坐舒适度评价是目前工程研究的一个新课题.文献［1－3］研究表明车辆与路面的耦合作用对车辆和路面振动的影响很大，在车辆与路面的相关动力分析中不可忽视.文献［4－5］研究表明侧向风荷载会使车辆受到横向力和倾覆力矩的作用，显著改变车辆的振动特性，特别是随着现代车辆行驶速度的提高，强侧向风荷载作用下车辆振动的安全性和舒适性问题会更加突出.文献［6－7］对侧风与桥梁振动对车辆乘坐舒适性影响进行了研究，但都采用车辆振动情况来评价车辆乘坐者的舒适感觉，忽略了人体与车辆结构耦合振动的影响，而文献［8］研究表明忽略人与结构的耦合作用难以准确地获得环境振动下结构和人体响应信息.本文将对侧向风荷载作用下考虑人体与车辆耦合作用和车辆与路面耦合作用的人－车－路系统振动响应问题进行探讨.

1 随机风场模拟

风荷载可分解为平均风和脉动风，平均风是在给定时间间隔内风力大小、方向等不随时间而改变的量；脉动风则随时间按随机规律变化，往往作为具有零均值的各态历经的高斯随机过程处理，风的模拟主要是针对脉动风而言.对于脉动风部分，借助经验公式给出的各种功率谱函数，可以从频域和时域两方面来分析.

本文脉动风功率谱采用Davenport谱［9］，表示为

令ρij为第i维脉动风和第j维脉动风的相干函数，根据Shiotani的建议，相关性可用如下形式的相干函数表达

式中：zi为模拟点的坐标；参数Lz＝60.

采用在工程领域广泛应用的谱解法对脉动风场进行模拟.假定路面沿水平方向等高程，平均风速和风谱沿路面不变，任意2个模拟风速点之间距离相等.路面第j个节点脉动风速时程由下式产生［10］式中：Δω＝（ωu－ωk）／N，ωu和ωk为截取频率的上限和下限，N为正整数，设为充分大.ωml＝（l－1）Δω＋mΔω／n；n为模拟的点数；φml为0和2π范围内的同一随机变数；Hjm（ωml）是由互功率谱密度函数矩阵S（ω）的 Cholesky分解得到；θjk（ωml）＝arctan［Im Hjm（ωml）／Re Hjm（ωml）］.

按常规方法计算最终的风速时程是很耗机时的，不建议直接采用，而引入FFT算法，将提高计算效率，式（3）可改写成

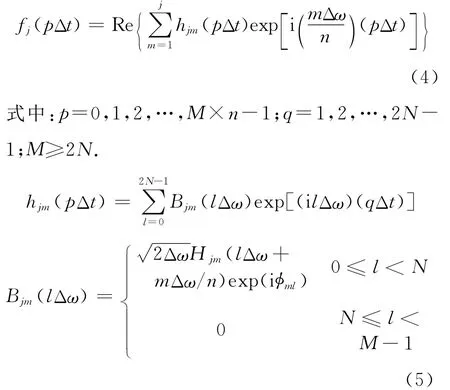
图1和图2分别为路面上某点平均风速为25m／s的自相关和互相关脉动风速曲线及其拟合功率谱与原始功率谱的对比，从图中可以看出，两者模拟效果均很好.

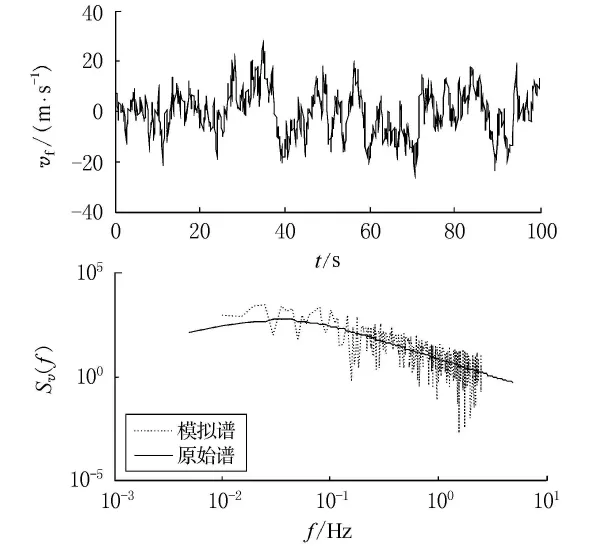
图1 脉动风速自相关时程曲线及其功率谱

图2 脉动风速互相关时程曲线及其功率谱

2 风荷载作用下系统振动方程

2.1 风车相互作用

风荷载包括顺着平均气流方向作用的推力及垂直于平均气流方向作用的升力.一般而言，总的风力的作用点、结构的弹性中心及质量中心不重合，因此结构也受到横向力矩的作用.即使处在对称气流中的对称结构也如此，因脉动风随机性使瞬时气流流动在通常情况下是不对称［10］.

假定风速垂直于道路的纵轴，作用于车辆上平均风速度和脉动风速分别为Um和u（x，t），车辆以恒定速度Uv行进，则风速与车辆的相对速度UR及偏角ψ可以表示为

2.2 系统振动方程

人体动力模型采用标准ISO 5982－1981［12］提供的竖向振动下人体坐姿下的并联动力模型；车辆模型采用7自由度全车模型，将车身和车轮视作刚体，车身具有浮沉、点头和侧滚3个自由度，每个车轮具有一个浮沉自由度；刚性路面采用Kelvin地基上的弹性梁进行模拟，模型示意图见图3.

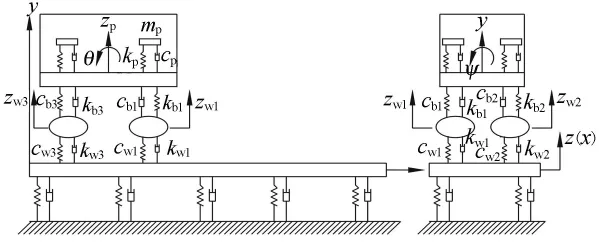
图3 人车路耦合系统模型

路面在车轮动态轮胎荷载的作用的方程为

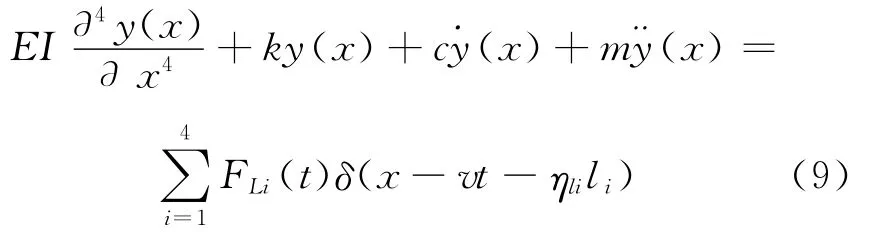
式中：FLi（t）＝cwi（－）＋kwi（zwi－zyi）；zyi＝y（vt＋ηlili）＋y0（vt＋ηlili）；y0（x）为路面初始不平整度，可采用数值方法进行模拟，参照文献［13］；zwi为车轮位移；该方程可采用模态叠加法进行离散.

根据达朗伯原理，人体与考虑点头和侧倾的七自由度车辆结构耦合振动系统动力平衡方程组为

将侧向风荷载式（8）添加到人体－车辆系统振动方程式（10）右侧荷载列中第二行，并与式（9）联合，即为侧向风荷载作用下考虑人体与车辆耦合作用的车辆与路面的耦合振动方程组，该方程组可采用New－Mark积分法进行求解.

3 舒适度评价方法

为了评价在频率为1～80Hz振动作用下的人体舒适度，国际标准组织发布了多个标准，如ISO 2631，本文采用其推荐的1／3倍频带法对车辆乘坐舒适度进行评价.

若人体的竖向振动加速度为¨zp（t），那么，自相关函数可以表示为

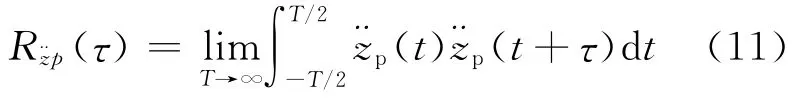
式中：T为响应时程的长度；τ为延迟时间.

人体的竖向加速度的功率谱密度函数可以通过自相关函数的傅里叶变换得到

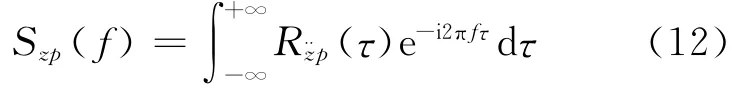
对应于频带中心频率fc的1／3倍频带中心频率的垂直加速度均方根值为

采用上述方法得到对应于中心频率的1／3倍频的加速度均方根，对于两自由度人体，计算出其加权平均值，就可以评价车辆乘坐者的舒适性.

4 仿真分析

用上述数值计算模型和分析理论，对侧向风荷载作用下，车辆在长为200m的路面上以20 m／s速度匀速行驶10s时系统的振动响应进行仿真分析.车辆参数参考文献［14］取值，参考有关文献［1］，路面宽度6m，路面厚度30cm，路面弹性模量E＝1.6×109Pa，路面密度ρ＝2.5×103kg／m3，路基反应模量k＝48×106Pa，路基阻尼系数c＝3.0×105N·s／m.

为研究侧向风速场对人车路系统振动响应的影响，进行了平整路面和A级不平整路面下无风、仅静态风、静态风＋自相关脉动风和静风＋互相关脉动风4种情况的对比分析.分析中平均风速为25m／s，计算结果见表1和表2.

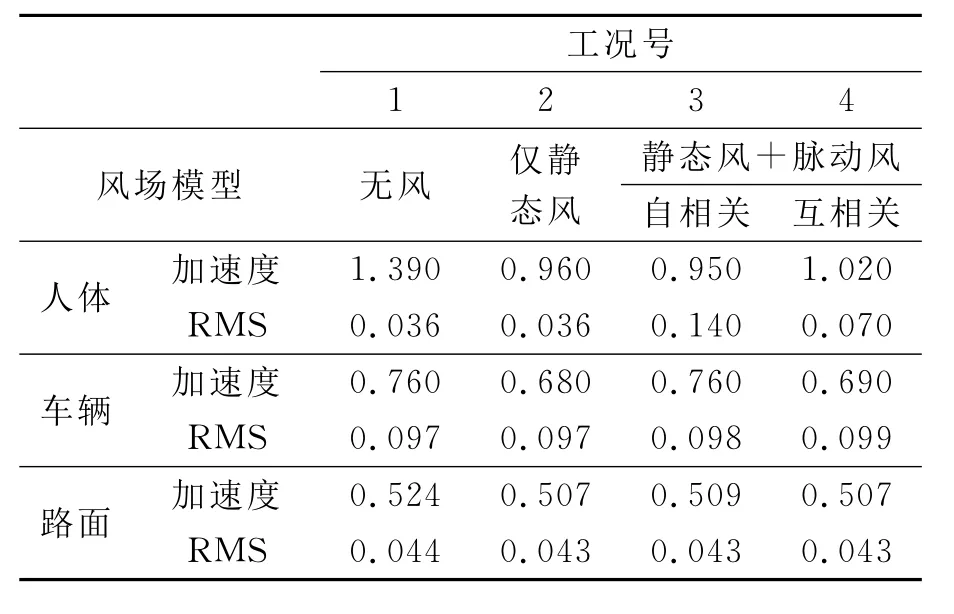
表1 平整路面下系统振动加速度响应 m／s2

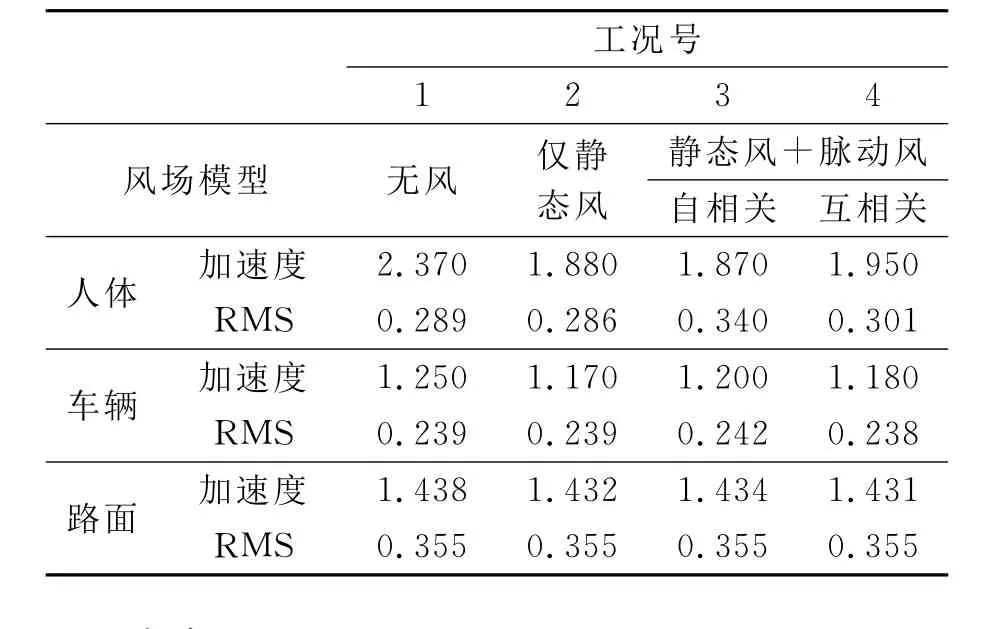
表2 不平整路面下系统加速度响应 m／s2

由表可见：

1）对比无风和仅静态风两种情况下的结果可以看出，在静态风荷载作用下人体、车辆竖向振动加速度响应最大值有所减少，这与静态风荷载的方向有关，但加速度均方根值却不变，也说明采用加速度均方根值评价车辆乘坐舒适度的必要性.

2）对比仅静态风和脉动风自相关两种情况下的结果可以看出，脉动风作用下人体振动加速度最大值增加不大，但均方根值却增大1.2～3.9倍，脉动风对车辆的振动影响不大；而且对平整路面下人车振动的影响比对不平整路面下的影响更明显.这说明采用采用车辆振动情况来评价车辆乘坐者的舒适感觉也是不正确的.

3）对比脉动风自相关和互相关两种情况下的结果可以看出，互相关脉动风作用下人体振动加速度最大值略有增大，但加速度均方根值却较小近12%～50%，但对车辆的振动影响不大.

4）风荷载场对路面结构的振动几乎没有影响.

为了分析侧向脉动风荷载的大小对车辆乘坐舒适度的影响，将对5种不同风速值的平整路面和A级不平整路面下车辆乘坐舒适度的变化情况进行分析，结果见图4.

图4 风速大小对乘坐舒适度的影响

从图中可以看出，随着侧向风速的增大，两种路面情况下乘坐舒适度均会增大，但风荷载大小对平整路面下的车辆乘坐舒适度影响会更显著；根据ISO 5982－1981标准，当风速达到55m／s时平整路面下车辆乘坐者会出现不舒适的感觉，在A级不平整路面时这个风速临界值为15m／s，这是由于路面不平度对车辆乘坐者振动加速度有一定程度的贡献，由此可推，当车速更大或者路面不平度等级更高时风速临界值会更低；可见，在高速公路上高速行驶的车辆考虑侧向风荷载对车辆乘坐舒适度的影响有更重要的意义.为了进一步分析车辆乘坐者出现不舒适感的主要反应，将对人体振动加速度的功率谱进行分析.图5分别为平整路面和A级不平整路面下人体振动加速度功率谱曲线，从图中还可以看出，风荷载对车辆乘坐者人体振动加速度的特性影响不大，并且两种路面情况下人体振动的频率范围均在1～10Hz，根据文献［15］可预测乘坐者出现不舒适感的人体生理反应主要为：头晕，肩部、脊柱振感较强及胸口发闷等.车辆乘坐者可事先采取措施以减轻不舒适感.

5 结 论

1）建立了侧向风荷载作用下人－车－路耦合振动模型，并对某小型汽车在路面运行过程中在模拟侧向风荷载作用的振动进行了仿真分析；风荷载对人体和车辆的振动影响较大，对路面结构的振动影响较小；而且对平整路面下系统振动的影响比对不平整路面下的影响更明显.

2）在静态风荷载作用下人体、车辆竖向振动加速度响应最大值有所减少，但均方根值却不变；脉动风作用下人体振动加速度最大值略有变化，但均方根值却增大1.2倍以上；脉动风对车辆的振动影响不大.互相关脉动风作用下人体振动加速度最大值略有增大，但加速度均方根值却减小12%～50%，但对车辆的振动影响不大.

3）随着侧向风速的增大，车辆乘坐舒适度会逐渐增大；平整路面下乘坐者出现不舒适感的临界风速为55m／s，A级不平整路面出现不舒适感的临界值为15m／s，当车速更大或者路面不平度等级更高时风速临界值会更低.

4）风荷载作用下车辆乘坐者的人体振动频率范围在1～10Hz之间，预测乘坐者出现不舒适感的人体生理反应主要为：头晕，肩部、脊柱振感较强及胸口发闷等.

［1］李韶华.重载汽车－路面－路基耦合系统动力学研究［D］.北京：北京交通大学，2008.

［2］张丙强，李 亮.车辆－路面耦合振动系统模型与仿真分析［J］.振动与冲击，2010，29（2）：35－38.

［3］张丙强，李 亮.人－车－路耦合系统振动分析及舒适度评价［J］.振动与冲击，2011，30（1）：1－5.

［4］李永乐.风－车－桥系统非线性空间耦合振动研究［D］.成都：西南交通大学，2003.

［5］CAI C S，CHEN S R.Frame work of vehiclebridge－wind dynamic analysis［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92：579－607.

［6］XU Y L，GUO W H.Effects of bridge motion and crosswind on ride comfort of road vehicles［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92：641－662.

［7］韩万水，陈艾荣.风－汽车－桥梁系统空间耦合振动研究［J］.土木工程学报，2007，40（9）：53－58.

［8］陈建英，方之楚.人－结构相互作用动力学建模研究［J］.振动与冲击，2007，26（6）：10－13.

［9］舒新玲，周 岱，王泳芳.风荷载测试与模拟技术的回顾及展望［J］.振动与冲击，2002，21（3）：6－10.

［10］李永乐，周述华，强士中.大跨度斜拉桥三维脉动风场模拟［J］.土木工程学报，2003，36（10）：60－65.

［11］葛玉梅，李永乐，何向东.作用在车－桥系统上风荷载的风洞试验研究［J］.西南交通大学学报，2001，36（6）：612－616.

［12］ISO.Vibration and shock－mechanical driving point impedance of the human body［S］.ISO 5982，1981.

［13］DODDS C J，ROSON J D.The description of road surface roughness［J］.Journal of Sound and Vibration，1973，31（2）：175－183.

［14］徐 娟，谭继锦，陈无畏.基于横向和垂向动力学的整车模型与仿真［J］.农业机械学报，2005，36（9）：9－11.

［15］何浩祥，闫维明，张爱林，等.竖向环境振动下人与结构相互作用及舒适度研究［J］.振动工程学报，2008，21（5）：446－451.