伺服系统中一种新型前馈控制结构的研究

2012-09-22，，，

电气传动 2012年2期

，，，

（南京工程学院自动化学院，江苏南京 211167）

1 引言

与步进驱动系统相比，正弦波永磁同步电动机伺服系统（简称交流伺服系统）具有环保、节能、快速、高精度的优势，但同时也存在跟踪误差较大的问题。数控机床上，在某一加工速度下，交流伺服系统跟踪误差的大小将直接决定加工目标的轮廓误差大小。对于高精度数控机床，在不影响刚度的情况下，当然希望交流伺服系统的跟踪误差越小越好。跟踪误差包括定位过程中的动态跟踪误差和定位结束后的静态跟踪误差。目前研究热点是如何降低动态跟踪误差。

学术界已经对改善交流伺服系统动态跟踪性能做了很多研究。文献［1－2］提出和总结了零相差跟踪控制（ZPETC）等先进控制策略，建议采用递推最小二乘法对交流伺服系统的转动惯量和粘滞摩擦系数进行在线估计并根据估计值对ZPTEC参数在线调整；文献［3－4］从交流伺服系统的闭环控制结构着手，针对不同应用场合，提出不同闭环控制结构，以优化系统动态跟踪性能。对于通用交流伺服系统，提高动态跟踪性能的最简单有效方法是采用反馈和前馈的复合控制［5］。根据控制理论，前馈控制可以提高闭环控制系统的跟踪性能。文献［6－9］反映了国内外交流伺服系统产品大多数都采用了速度前馈信号作用在速度闭环给定信号上的前馈控制方法，文献［10］对加速度在交流伺服系统中的作用也作了初步分析。本文从数控系统中交流伺服系统的命令信号形式着手分析加速度信号对交流伺服系统动态跟踪性能的影响，并提出速度前馈信号作用在速度闭环给定信号上、加速度前馈信号作用在转矩（即q轴电流）闭环给定信号上的新型前馈控制方法，举例数控系统中常用的梯形给定和S曲线给定，分析、仿真和实验了新前馈控制方法下交流伺服系统的动态跟踪性能。

2 前馈复合控制

目前在交流伺服系统位置闭环调节器广泛采用比例和前馈复合控制结构，如图1所示。图1中，Kv是速度闭环等效惯性环节的增益；τv是速度闭环等效惯性环节的时间常数；Kθ是编码器反馈系数；F（s）是前馈传递函数。

图1 前馈和反馈复合控制的位置伺服系统结构图Fig.1 Chart of position servo system in feedback and feedforward composite control

图1中，为了实现输出信号对输入信号的完全跟踪，则前馈到输出之间的传递函数为1，即

从而推出

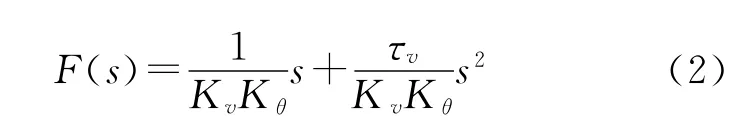
由式（2）可以看出，位置前馈函数由2部分组成，分别为速度前馈函数和加速度前馈函数。令位置闭环调节器中速度前馈系数为Kvff，加速度前馈系数为Kaff，则

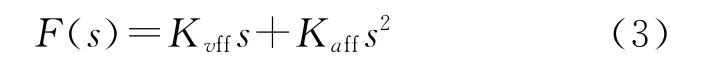
根据图1，可以求得采用比例加位置前馈复合控制策略下，位置跟踪误差的传递函数为

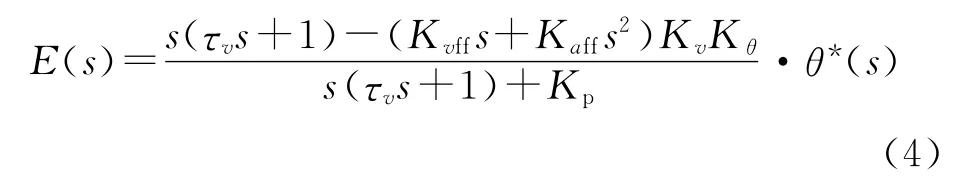
数控系统中，交流伺服系统的命令信号是先加速，其次恒速（也可以没有恒速段），再减速，最后恒速（如果是零速，表示定位过程结束）。在恒速段，位置给定信号为

式中：v为恒速段速度值。

则恒速段内的稳态位置跟踪误差为

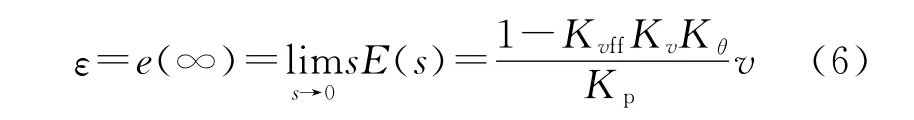
令

由式（6）可以看出，当速度前馈系数取式（7）所示值时，理论上可以使恒速段的稳态位置跟踪误差减小到零。式（4）与式（6）比较，可以看出，采用比例和位置前馈复合控制方法，比采用纯比例调节器时，交流位置伺服系统的跟踪性能可以得到大大提高。

未加前馈控制，位置闭环仅采用纯比例调节器时，梯形响应中恒速段稳态位置跟踪误差的幅值较大，例如高速恒速段的稳态位置跟误差ε＝1 267个脉冲，加减速段的位置跟踪误差曲线都比较平滑，如图2所示。图2中KPP＝40，Kvff＝0，Kaff＝0，位置反馈用编码器为2 500个脉冲／转，且经过DSP 4倍频。本文中所有实验均在伺服电机空载的情况下完成，实验波形都是通过VB软件来实时接收交流伺服系统的实际位置信号和实际位置跟踪误差信号，然后绘图得到。当加入位置前馈控制后，恒速段的稳态位置跟踪误差的幅值很小甚至接近于零，这时加速段和减速段中的动态位置跟踪误差以及加速度值突变引起的动态跟踪误差显现出来，造成了梯形响应中位置跟踪误差曲线的非单调变化，如图3中各种响应波形所示。图3a中KPP＝40，Kvff＝0.9，Kaff＝0，图3b中KPP＝40，Kvff＝1，Kaff＝0，图3c中KPP＝40，Kvff＝1.1，Kaff＝0。根据位置前馈对位置跟踪误差的补偿程度，即根据恒速运行段的稳态位置跟踪误差ε值的大小，位置前馈复合控制的系统可以工作在3种状态：调节器选取Kvff＜Kx时为欠补偿状态，有ε＞0；选取Kvff＝Kx时为完全补偿状态，有ε＝0；选取Kvff＞Kx时为过补偿状态，有ε＜0。

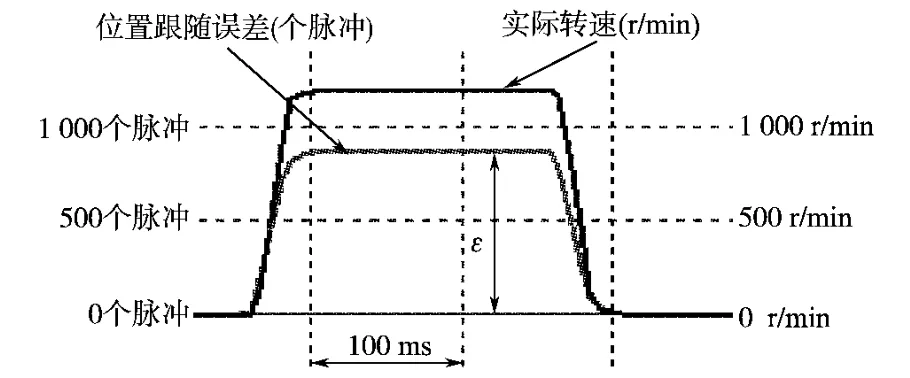
图2 梯形响应中纯比例调节器时跟踪误差实验波形Fig.2 Waves of speed and position tracking error in trapezium response for only proportion regulation

图3 梯形响应中前馈复合控制时跟踪误差实验波形Fig.3 Waves of speed and position tracking error in trapezium response for feedforward composite control

根据数控机床减小轮廓误差的要求，交流伺服系统采用速度前馈全补偿方式。此时，调节Kaff的值，加速段和减速段的位置跟踪误差却没有发生太多变化。根据式（1），交流伺服系统不管在恒速段还是在加减速段，都可以实现完全跟踪。但式（1）的前提是把速度闭环等效成一阶惯性环节，而实际上速度闭环是个内部还包括有转矩闭环的高阶系统。另外，在速度闭环的PI调节器中，只有P或I参数刚好在某个值时才能使速度闭环等效成一阶惯性环节。而实际中，P或I参数是根据现场实际负载进行调试后得到的参数值，不可能时刻满足速度闭环等效成一阶惯性环节的条件。所以加速度前馈作用在速度闭环的给定信号上，在实际中很难真正起到降低加速段和减速段的位置跟踪误差的作用。那么，为了使整个定位过程中的位置跟踪误差都尽量接近于零，如何抑制加速段和减速段的位置跟踪误差呢？

3 转矩前馈设计

将图1中等效的速度闭环进行还原，并且将转矩闭环等效成一阶惯性环节，得到位置伺服系统的控制结构图如图4所示。从通常意义上来理解，相同的PID参数情况下，恒速段位置跟踪误差与传动机构摩擦转矩有关。而在加减速段，位置跟踪误差不仅与传动机构中摩擦转矩有关，还与伺服电机转子轴上转动惯量的大小有关。而提高转动惯量的加减速能力，就必须增加转矩大小，或增加转矩命令信号的提前量，也就是转矩前馈。基于以上考虑，提出如图5所示的新型前馈复合控制结构：速度前馈作用在速度闭环的给定信号上，同时命令信号中的加速度信息（即转矩前馈信号）作用到转矩闭环给定信号上。

图4 转矩闭环等效成一阶环节时位置伺服系统结构图Fig.4 Chart of position servo system when torque closedloop equivalent to one－order linker

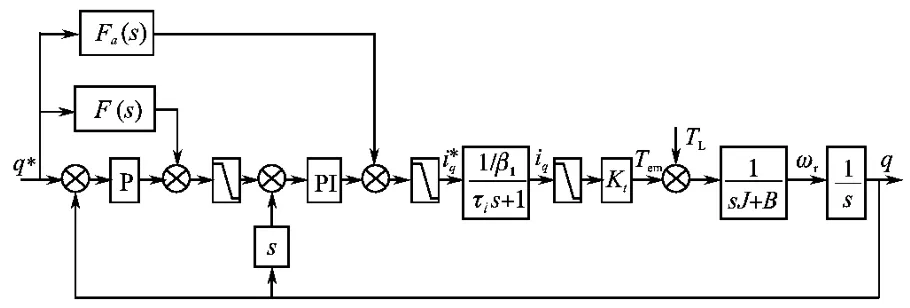
图5 基于新型前馈控制的位置伺服系统结构图Fig.5 Chart of position servo system in the novel feedforward control

图5所示结构中，分析速度前馈的作用与图1结构下的分析是一致的，速度前馈全补偿时，恒速段的稳态位置跟踪误差可以接近于零。如果要保证加、减速段的位置跟踪误差也接近于零，则转矩前馈通道的所有传递函数乘积等于1。并且转矩前馈主要用来抑制转动惯量引起的位置跟踪误差，所以可以近似认为粘滞系数B＝0，则可以得：

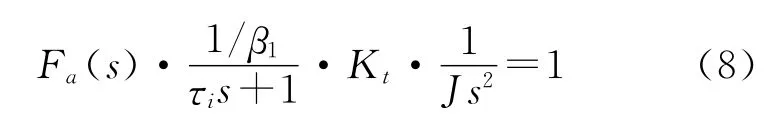
由式（8）可得到下式：

将速度闭环等效成一阶惯性环节时，添加在速度闭环给定信号上的前馈作用由2部分组成，如式（2）所示。相同地，将转矩闭环等效成一阶惯性环节时，添加在转矩闭环给定信号上的前馈作用也由2部分组成，如式（9）所示，分别为转矩前馈分量本身Jβ1s2／Kt和加加速度前馈Jβ1τis3／Kt。令添加到电流闭环给定信号上的转矩前馈系数和加加速度前馈系数分别为Kaff1和Kaaff，则理论上：

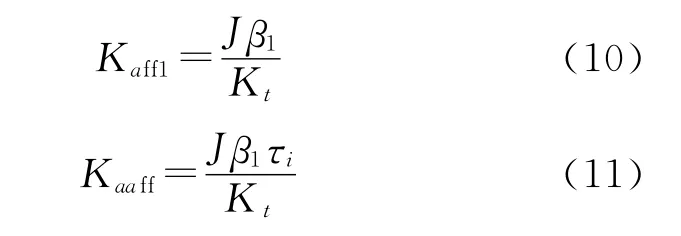
当实际中设定KPP＝40，Kvff＝0.9，Kaff＝0，Kaff1＝0.006 9，Kaaff＝0时，交流伺服系统在图5所示的控制结构下得到的梯形响应实验波形如图6所示。图6与图3b比较，说明在增加了转矩前馈后，交流伺服系统梯形响应中，加减速段的位置跟踪误差明显减小，幅值由增加前的25个脉冲，降低到了增加后的4个脉冲，定位过程的整定时间也大大缩短。

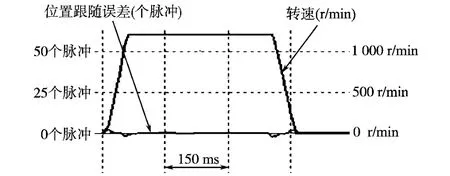
图6 新前馈控制结构下梯形响应实验波形Fig.6 Experimental waves of trapezium response in the novel feedforward control

4 加速度突变的影响和S曲线响应

在数控系统中，插补器作精插补后输出给各个轴驱动器的速度命令信号最常用的是梯形命令信号和S曲线加减速命令信号（简称S曲线命令信号）。梯形信号中，在加速或减速的起点和终点，都存在加速度信号突变，这个突变会对伺服系统产生柔性冲击，从而造成动态位置跟踪误差，如图6中位置跟随误差曲线在加速度突变点处的波动。

从位置给定信号的组成来讲，加速度突变实际上就是加加速度（加速度时间函数的导数）不等于零。而3闭环控制结构中，没有加加速度的调节闭环，所以系统不能依赖前馈控制来抵消加加速度引起的位置跟随误差，而只能通过反馈控制系统中的位置闭环比例系数大小来调节加加速度引起的位置跟随误差的大小。在此，前馈控制不能发挥作用。

S曲线命令信号就是从控制器的命令信号着手来解决加速度突变的问题。S曲线信号中，没有加速度突变。交流伺服系统设定在图6相同的条件下，S曲线响应实验波形如图7所示。