雷达伺服系统的混合智能算法应用及其鲁棒性分析

，，

（安徽大学 电气工程与自动化学院，安徽 合肥 230039）

1 引言

目前我国成型雷达装备中，控制电路伺服系统多采用基本PID控制，有的回路甚至是PI控制。虽结构简单可操作性强，但可调参数少，超调量大调节时间长［1］。

对伺服系统控制算法的优化一直是控制理论的研究热点。Gawronski.W对70－m雷达天线的机电伺服控制系统应用LQG算法［2］。Karam M .Elbayomy对电液运动伺服系统用遗传算法GA优化PID参数增益［3］。国内研究人员也针对雷达伺服系统做了众多工作［4－5］，遗憾的是多为仿真研究。

本文针对某型号雷达的伺服系统，引入前馈控制和模糊PID控制共同构成的混合智能控制算法代替传统PID控制。分析了控制系统的数学模型及其稳定性和鲁棒性，并在实际雷达伺服系统中运行该算法，实验证明混合智能控制算法可以达到很好的控制效果，提高了系统的准确性。

2 混合智能控制算法及控制系统数学模型

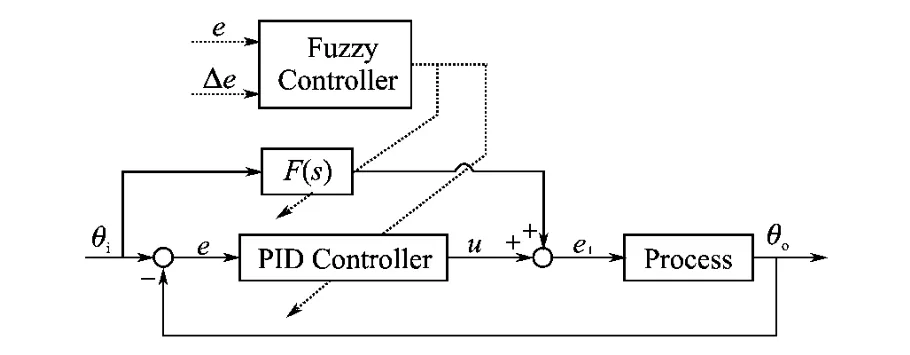
图1 基于前馈补偿和模糊控制的智能控制系统框图Fig.1 Block diagram of intelligent control system based on feed－forward compensator and fuzzy control

图1给出了雷达伺服系统的混合智能控制方框图。其中θi为输入角位置信号，θo为输出的角位置信号，F（s）为前馈补偿装置的传递函数。同时利用模糊控制规则调节前馈和PID控制器的参数，构成混合智能控制。

2.1 前馈的数字实现形式

图1中前馈补偿F（s）的数字实现形式为

其中

式中：kv为速度前馈增益；ka为加速度前馈增益。PID控制器的递推实现形式：

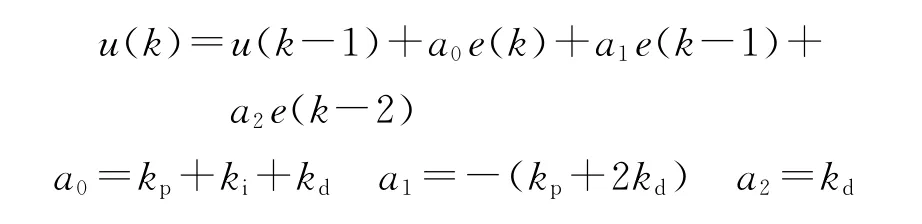
工程实践通常采用PI控制，即

其非递推形式可用下式描述：

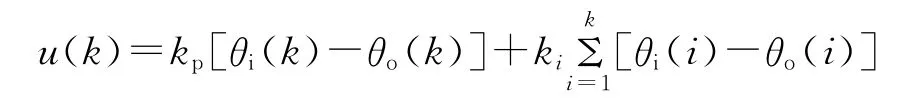
增加前馈补偿后的数字实现为

传统的PID控制器调节有限，且常常造成跟踪的延迟；前馈补偿的引入等效于提高了伺服系统的阶数，可加快系统动态响应，减少动态误差。速度前馈和加速度前馈的引入分别影响伺服系统位置环和速度环；当前馈速度增益kv和前馈加速度增益ka越大，位置误差的累计值和速度误差的累计值就越小［6］。

2.2 模糊PID控制

采用前馈有效地提高了伺服系统的响应速度，但是在实际工程应用时，很难得到一个合适的前馈传递函数使得伺服系统实现完全不变性，通常还会引入较多噪声。在伺服系统调试过程中发现引入前馈后的伺服系统常常会产生振荡和位置超调，影响系统的稳定性。为了解决该问题，引入模糊控制。通常模糊控制与PID控制相结合的思路有两种：一是在偏差较大时利用模糊推理的方法调整系统的控制量U，而在小偏差范围内切换成PID控制，此为调整系统控制量的模糊PID控制器；二是利用模糊规则和推理对PID参数进行调整，构成模糊增益调整PID控制器［7］。

本系统采用第2种方式，以误差信号e和误差增量Δe为输入量，以前馈增益ka，kv为输出量。论域、模糊子集及隶属函数的选择；模糊控制规则与模糊控制查询表；模糊控制器的输出曲面等信息作者在文献［8］中已有详细说明，本文不做赘述。在此主要是建立被控对象和智能控制器的整体数学模型，并对其稳定性和鲁棒性进行理论分析。

2.3 控制系统数学模型

将电流环、速度环组成的连续被控对象离散化得［1］：

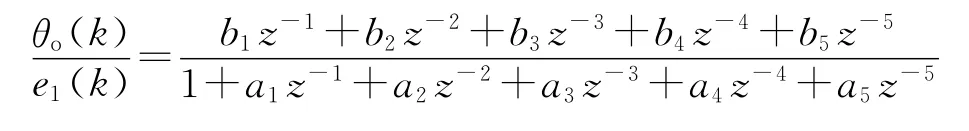
则描述系统的方程组为

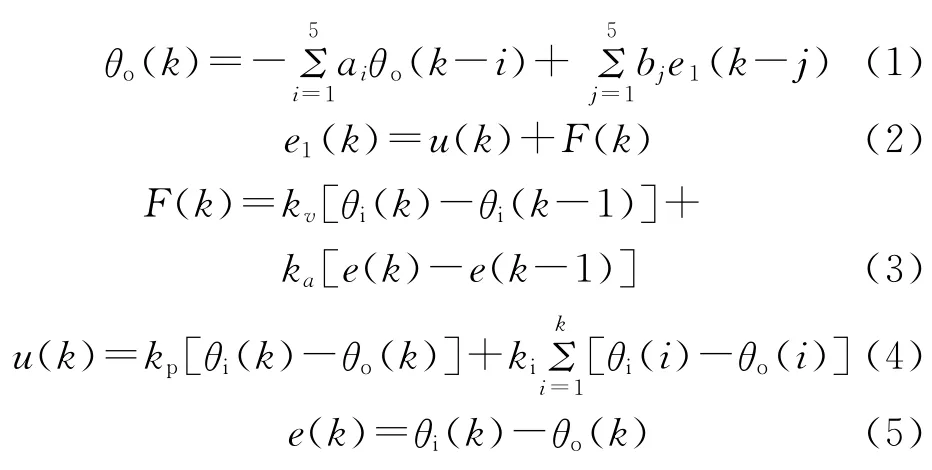
由以上方程组得输入输出量之间的差分方程描述数学模型：

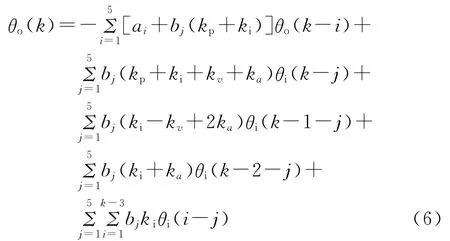
其中，kv，ka遵从文献［8］模糊控制规则，随e（k）和Δe（k）的输入，根据模糊控制规则表取不同数值。PID参数kp，ki的选取也随着e（k）和Δe（k）而做出整定。

3 混合智能控制系统鲁棒性和稳定性分析

由于摩擦系数、转动惯量等测量和标定的误差等因素，用于设计的对象模型不可避免存在一定的误差，经分析可用被控对象模型的参数摄动表示其不确定性（可参数化不确定模型）［9］，则实际模型可简化为

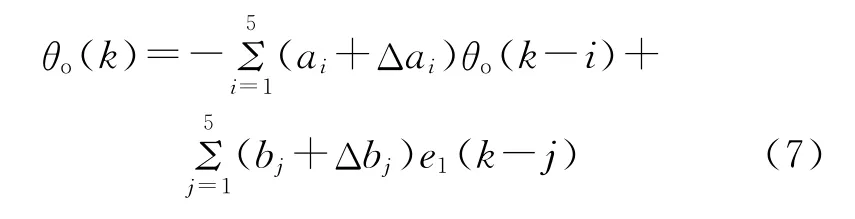
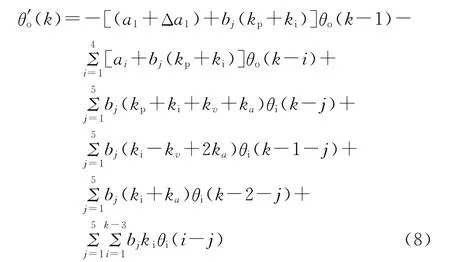
模型输出误差为

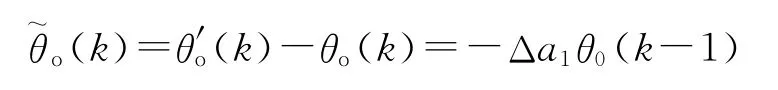
则模糊控制器的输入e（k）增加Δa1θo（k－1），根据模糊控制的规则参数kp将增加，若kp增加至kp＋ki＋Δai／bj或此值附近，可使系统输出在上述参数摄动下保持不变，即θo（k）≈θ′o（k）。扩展至其他参数摄动，亦可用模糊控制保证整个系统的鲁棒性。

令Θo（k）＝ ［θo（1），…，θo（k）］T，Θi（k）＝［θi（1），…，θi（k）］T，则上述系统可描述为

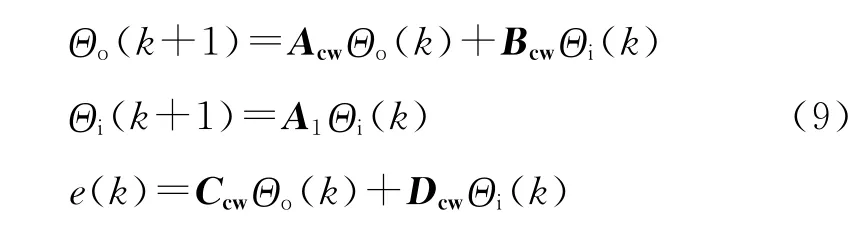
矩阵Acw，Bcw，Ccw，Dcw由参数ai，bj和kv，ka，kp，ki决定。

（G1，G2）为矩阵A1的p－copy内模，且G1满足对所有λ∈σ（G1），有：

4 实验结果及分析

编写程序分别将原PID控制算法、引入前馈补偿的算法、由前馈控制和模糊PID共同构成的智能控制算法，应用到雷达伺服跟踪系统中。模糊控制表可由计算机事先离线算好，存储于计算机中，以实现实时控制。在检飞试验中，为了对比3种控制算法的优劣，选取一段过顶目标进行伺服跟踪，因为此时天线的角速度和角加速度最大。图2、图3、图4为试验中的截图，其分度为对数分度。可以看出在时间11∶54∶10至11∶54∶20约10s跟踪误差较大，此时目标为正过顶，跟踪角速度和角加速度超出设计指标，此段试验数据不采用。

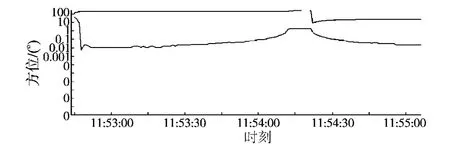
图2 PID控制下系统的角误差输出曲线Fig.2 The angular error of tracking output under PID controller

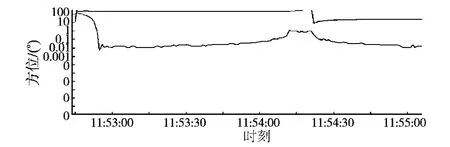
图3 前馈控制角误差输出曲线Fig.3 The angular error of tracking output under feed－forward controller

图4 混合智能控制角误差输出曲线Fig.4 The angular error of tracking output under hybrid intelligent controller

因截图纵坐标为不均匀的对数分度，对比不明显；将3组试验数据存储后在另一均匀坐标系下共同绘制出，如图5所示，曲线1，2，3分别对应图2、图3、图4中数据。

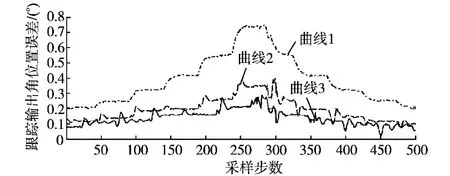
图5 各种控制算法下系统的角位置偏差输出Fig.5 The angular errors of tracking outputs under three control algorithm

试验结果表明，当角速度和角加速度较小时，3种控制策略的控制效果相近。

当速度和加速度较大时，传统PID控制（图5中曲线1）的跟踪精度最差，最大跟踪误差达到0.7°，跟踪能力较差。

引入前馈补偿控制（图5中曲线2）的最大跟踪误差只有0.39°，跟踪精度显著提高。但是，当加速度较大时，伺服系统会产生振幅约0.1°的振荡，伺服系统的鲁棒性变差。在更加精密的跟踪要求下，这种震荡是不希望出现的。

由前馈补偿和模糊PID控制构成的混合智能控制（图5中曲线3）的最大跟踪误差为0.27°，不仅提高了伺服动态性能，也有效抑制了纯前馈控制时出现的震荡，过渡过程品质得到提高。

5 结论

通过理论分析和飞行试验，验证了由前馈控制和模糊PID控制构成的混合智能控制策略的有效性。试验结果表明该算法可以提高雷达伺服系统的控制精度，改善了动态性能；且易于实现，具有很高的工程应用价值，可应用于类似伺服系统中。

［1］王振收.机载SAR稳定平台直流力矩电机驱动器［J］.现代雷达，2006，28（3）：70－75.

［2］Wodek Gawronski，Harlow G Ahlstrom，Jr Abner M Bernardo.Analysis and Performance of the Control Systems of the NASA 70－meter Antennas［J］.ISA Transactions，2004，43（4）：597－610.

［3］Karam M Elbayomy，Jiao Zongxia，Zhang Huaqing.PID Controller Optimization by GA and Its Performances on the Electro－hydraulic Servo Control System［J］.Chinese Journal of Aeronautics，2008，21（4）：378－384.

［4］李荧星，贾彦斌.基于内模控制的稳定系统设计与仿真［J］.系统仿真学报，2005，17（12）：58－60.

［5］李凤俐.时间最优控制理论在雷达伺服系统中的应用［J］.测控技术，2008，27（6）：47－49.

［6］Richard C Dorf，Robert H Bishop.Modern Control Systems［M］.（9th ed），USA：Pearson Higher Education，2002.

［7］张国良，邓方林.模糊控制及其 MATLAB应用［M］.西安：西安交通大学出版社，2002.

［8］Wang Qun－jing，Zhang Qian.Intelligent Combined Control Applied on Radar Servo System［C］∥3rd International Conference on Computer and Electrical Engineering （ICCEE 2010），2010，2（11）：498－501.

［9］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2003.

［10］Huang Jie.Nonlinear Output Regulation Theory and Application［M］.Hong Kong：Society for Industrial and Applied Mathematics，2004.