感应电机DTC自适应磁链闭环辨识

，，，

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.长沙毅超自控技术有限公司，湖南 长沙 410082）

1 引言

感应电机直接转矩控制（DTC）是德国 M.Depenbrock教授在1985年首先提出的，它摒弃了矢量控制中解耦的思想，采用转矩和定子磁链两个滞环式控制环和预先编制的电压开关矢量表实现对定子磁链与转矩的直接控制。DTC系统的这种控制方式需要实时检测定子磁链与转矩，由于直接检测定子磁链存在一定的难度，目前常用的方法是利用电机端电压和电流辨识定子磁链。定子磁链辨识模型包括［1］：电流模型、电压模型以及自适应磁链辨识模型。电流模型根据定子电流和速度来估计磁链，这种辨识器需要检测速度，还涉及到易受影响的转子时间常数慢时变参数，使得参数辨识变得十分复杂。电压模型尽管只需要检测电机定子电压和电流，但这种基于电机稳态电压模型的定子磁链开环辨识方法存在纯积分器带来的直流偏置累积误差，造成定子磁链辨识值不准确的问题。为了精确辨识定子磁链对积分器饱和问题人们展开了深入研究［2－6］，文献［2］在DTC中引入一个速度偏差的定子磁链PI校正补偿环节，这一方法由于速度检测或辨识算法复杂，使得实现难度较大。文献［3］利用低通滤波器代替纯积分器消除积分饱和误差，但带来定子磁链幅值和相位的附加误差，特别在低频或工作频率低于低通滤波器截止频率时，产生的误差不能忽略。文献［4］研究一种补偿低通滤波器定子磁链幅值和相位误差的算法，但此方法只适用于稳态情况。文献［5］提出一种结合了电压模型和电流模型优点的复合模型。随着自适应控制等技术的不断发展，目前还出现了如自适应观测器、滑模观测器等定子磁链辨识方法［6］，但这些方法比较复杂，实时性不好。

本文为了提高定子磁链辨识的自适应能力，研究了一种基于均值补偿算法的定子磁链闭环自适应辨识方法，并构建了基于DSP控制的DTC系统，进一步验证定子磁链闭环自适应辨识方法的正确性。

2 定子磁链自适应辨识器

针对定子磁链积分饱和问题，本文提出的基于定子磁链闭环自适应辨识的DTC系统原理框图如图1所示。

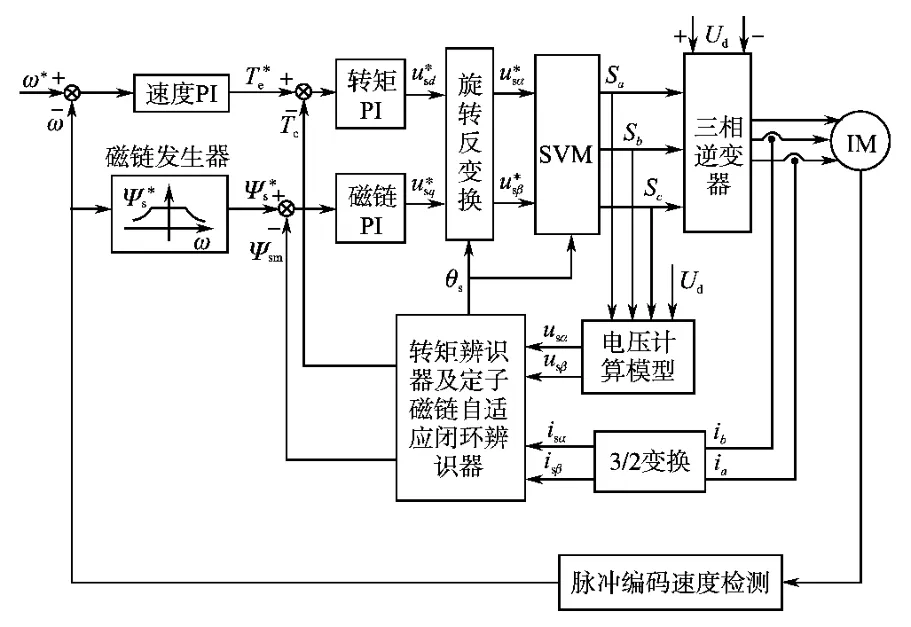
图1 基于定子磁链自适应辨识的DTC系统Fig.1 DTC system based on adaptive stator flux identification

图1中，由转矩辨识及定子磁链自适应辨识环节计算实际磁链Ψsm和转矩Te；采用磁链与转矩PI调节器实现磁链与转矩误差跟踪控制；利用DTC－SVM产生PWM。图2给出定子磁链自适应闭环辨识器的结构框图。

2.1 定子磁链均值补偿算法

本文将定子磁链分解为1个标准正弦波和1个直流偏置，其标准正弦波部分在每个周期内的平均累加值为0，而直流偏置部分在每个周期内的均值就是该周期的累积误差。如将每个周期内的均值从积分器的输出中减去，就可消除累积误差，以下建立定子磁链均值补偿算法。

图2 定子磁链自适应闭环辨识器Fig.2 Adaptive stator flux closed loop identifier

感应电机DTC在定子静止αβ坐标系中的定子电压方程为

由式（1）导出辨识定子磁链的电压模型为

为计算每一周期定子磁链直流偏置累积误差，设逆变器输出电压的频率为f，周期T＝1／f，DTC循环周期设为Ts。则电机反电动势在α，β轴上的表达式为

式中：Esm为反电动势幅值；Eαdc，Eβdc分别为α，β轴上的直流偏置。

纯积分器每一周期T末的输出为

1个周期内的定子磁链均值为

其中，k是T／Ts的取整值，通常电机低速时的k值较大。

补偿后的定子磁链值为

基于以上原理设计的定子磁链均值补偿算法如图3所示。

图3 定子磁链均值补偿算法Fig.3 Stator flux mean compensation algorithm

图3中，Sc为补偿控制信号是1个周期内累积误差的计算值；是在1个周期末含有累积误差的定子磁链值；Ψs是在1个信号周期末不含累积误差的定子磁链值。推导可知，均值补偿方法能有效消除1个周期内的定子磁链积分累积误差，但对1个周期内的瞬时不确定干扰无补偿作用。

2.2 定子磁链闭环自适应辨识算法

为消除积分器1个周期内的瞬时直流偏置误差，本文设计一种自适应闭环校正环节消除实时误差。

定子磁链Ψs在α，β轴上的分量分别为

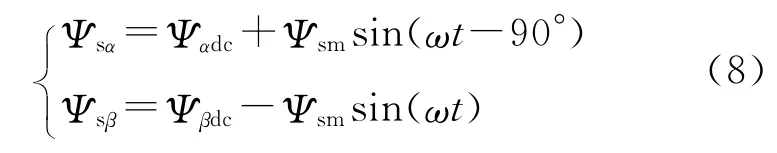
Es和Ψs矢量的点积为

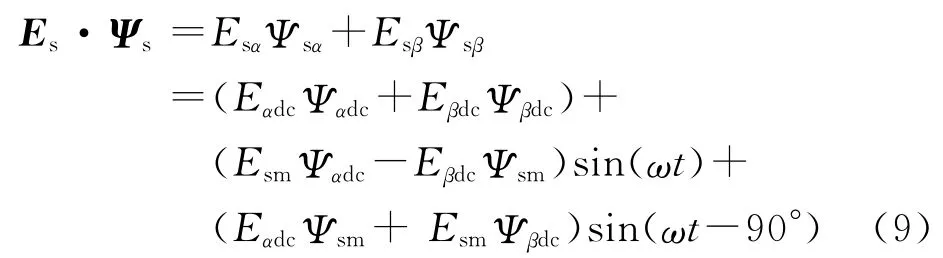
当电机反电动势中出现直流偏置时，式（9）中将产生与定子磁链具有相同频率的交流分量。为此引入自适应辨识闭环校正算法，PI调节器输出的定子磁链校正系数为

式中：kP，kI为比例积分的常数；γ为Es和Ψs的夹角。

当PI调节达到稳态时，意味着Es和Ψs点积的直流分量已为零。即：补偿后的α轴定子磁链的直流偏置等于（kPIΨsα）补偿值与α轴带直流累积误差的定子磁链之和。即：

式中：k0为PI输出的直流分量。

稳态时，可以求得：

从式（13）不难看出，定子磁链的直流偏置与电机反电动势的直流偏置成正比，表明这种自适应磁链闭环辨识校正算法可以有效地消除初始值积分误差和直流偏置在定子磁链上产生的积分累积误差。

3 仿真与实验结果

在Matlab／Simulink仿真环境下建立基于定子磁链闭环自适应辨识器的仿真模型如图4所示。

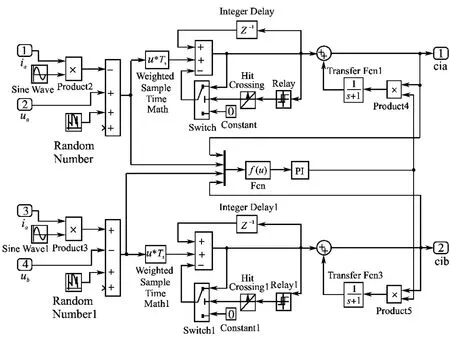
图4 定子磁链闭环自适应辨识器仿真模型Fig.4 Simulation model of adaptive stator flux closed loop identifier

为了研究定子磁链自适应闭环辨识器对扰动的自适应能力，这里用一个随机函数来表示定子电阻从0.5Rs到1.5Rs的扰动，PI调节器的参数kP＝0.1，kI＝20。图5给出随机扰动时定子磁链圆形轨迹响应曲线。

图5中，在随机扰动时，定子磁链自适应闭环辨识器获得的定子磁链轨迹逼近圆形，定子磁链的辨识精度较高，误差较小。

速度在从300r／min跳跃到1 000r／min时的磁链变化情况如图6和图7所示。

图5 定子磁链圆形轨迹Fig.5 Stator flux circular trajectory

图6 纯积分器辨识的定子磁链曲线Fig.6 Stator flux curve of pure integrator identifier

图7 自适应辨识的定子磁链曲线Fig.7 Adaptive identifier stator flux curve

从图6和图7中可以看出，速度阶跃时，纯积分器辨识出的定子磁链波形在1s时有明显的失真并最终趋向于饱和。而定子磁链自适应闭环辨识器的定子磁链波形基本上保持了正弦，证明了定子磁链自适应闭环辨识器具有较好的自适应能力。

为了验证定子磁链自适应闭环辨识器的正确性，本文建立了基于dsPIC30F6010A控制的感应电机DTC数字化控制实验研究平台。

实验用感应电机参数为：额定功率PN＝4 kW，额定频率fN＝50Hz，额定转速nN＝1 430 r／min，转动惯量J＝0.013 1kg·m2，电机极对数np＝2，定、转子互感Lm＝0.172 2H，转子自感Lr＝0.005 839H，定子自感Ls＝0.005 839H，转子电阻Rr＝1.395Ω，定子电阻Rs＝1.405Ω。实验中设定的控制系统参数为：DTC主程序循环周期为80μs；DSP的时钟频率为29.491 2MHz；DTC开关频率为10kHz。

图8、图9给出了定子磁链闭环辨识器的DTC系统实验波形。图8给出了纯积分定子磁链辨识器的定子磁链幅值波形；图9给出了基于定子磁链自适应闭环辨识器的定子磁链幅值波形。

图8 纯积分辨识器的定子磁链幅值Fig.8 Stator flux amplitude of pure integrator stator flux identifier

图9 定子磁链闭环自适应辨识的定子磁链幅值Fig.9 Stator flux amplitude of adaptive stator flux closed－loop identifier

通过比较图8和图9可知，图8中的定子磁链幅值响应有一定的超调并存在静态误差，而图9中定子磁链幅值的动态响应性能得到较大改进且静态误差较小，验证了改进的定子磁链辨识器具有较好的动态校正能力和跟踪定子磁链幅值变化能力，其稳态辨识精度也较高。

4 结论

本文研究了基于均值补偿的定子磁链自适应闭环辨识方法。仿真结果表明：这种自适应方法在消除积分饱和累积误差等方面获得了较好的效果。在理论分析与仿真研究的基础上，本文采用DSP构成的基于定子磁链自适应闭环辨识的DTC系统进行实验研究，实验结果证明这种定子磁链闭环辨识器不仅能有效地消除积分累积误差和不确定干扰误差，而且具有辨识精度高和动态跟踪自适应特性好等优点。

［1］Habibur R，Derdiyuk A，Guven M K，etal.A New Current Model Flux Observer for Wide Speed Range Sensor Less Control of an Induction Machine［J］.IEEE Trans.Power Electron.，2002，17（6）：1041－1048.

［2］Kuo Kai Shyu，Li Jen Shang，Hwang Zhi Chen，etal.Flux Compensated Direct Torque Control of Induction Motor Drives for Low Speed Operation［J］.IEEE Transaction on Power Electronics，2004，19（6）：1608－1613.

［3］Hurst K D，Habetler T G，Griva G，etal.Zero Speed Tacholess IM Torque Control：Simply a Matter of Stator Voltage Integration［J］.IEEE Transactions on Industry Applications，1998，34（4）：790－795.

［4］Nik Rumzi Nik Idris.An Improved Stator Flux Estimation in Steady State Operation for Direct Torque Control of Induction Machines［J］.IEEE Transaction on Industrial Application，2002，38（1）：110－116.

［5］Choi Youn Ok，Lee Kang Yeon，Seo Kang Sung，etal.Performance Analysis of the DTC Using a Closed Loop Stator Flux Observer for Induction Motor in the Low Speed Range［C］∥In：Proceedings of the Fifth International Conference on Electrical Machines and Systems，ICEMS，2001，1：89－93.

［6］Salmasi F R，Najafabadi T A，Maralani P J.An Adaptive Flux Observer with Online Estimation of DC－link Voltage and Rotor Resistance for VSI Based Induction Motors［J］.IEEE Transaction on Power Electronics，2010，25（5）：1310－1319.