振动半圆柱尾流中的二维摆动水翼推进性能研究

张 曦，苏玉民，王兆立

（哈尔滨工程大学 水下智能机器人国防科技重点实验室，哈尔滨 150001）

1 引 言

经过数千亿年的进化，鱼类等海洋生物具有在水中高效快速游动的能力。特别是在复杂流场中，鱼类通过改变运动姿态来保持高效率的游动。已经有学者发现，鱼类能够利用鱼体附近的旋涡，并从旋涡中吸收能量[1]。反观诸如螺旋桨等传统推进装置，它们都不能很好地适应复杂流场。近些年来，已经有许多躯体-尾鳍模式（Body and Caudal Fin,BCF模式[2]）的仿生推进装置用于小型水下航行器。美国麻省理工大学已经研制出利用旋涡提高推进性能的水下航行器VCUUV[3]。在VCUUV的基础上，美国海军研制出了世界上最快、最灵活的"金枪鱼"潜水器，该潜水器在实验过程中的优异表现已经引起了各国的重视。因此对BCF模式仿生推进装置在复杂流场中，特别是在受到旋涡影响时的推进性能进行研究就显得非常必要。

许多学者采用数值或实验手段研究了旋涡对BCF模式仿生推进装置的影响。在这些研究中，BCF模式仿生推进装置通常被简化为同时作升沉运动和摇摆运动的摆动水翼。Streitlien[4]在流场中布置点涡，应用势流理论研究了点涡对二维摆动水翼水动力性能的影响。研究发现二维摆动水翼能够从点涡中吸收能量从而提高推进效率。Gopalkrishnan[5]将大展弦比的摆动水翼置于卡门涡街中，从而找到了几种旋涡和水翼涡相互作用的模式。Beal[6]也作了类似于Gopalkrishnan的实验，实验结果表明摆动水翼能够吸收旋涡中的能量从而提高推力。Zhu等人[7]采用三维非线性面元法研究了摆动尾鳍在鱼体脱落涡影响下的水动力性能，指出尾鳍可以利用鱼体脱落涡提高推进性能。

本文二次开发了基于有限体积方法求解雷诺平均纳维—斯托克斯（RANS）方程的CFD软件FLUENT，计算了振动半圆柱后方二维摆动水翼的水动力性能。在求解过程中采用了动网格技术。分析了旋涡相互作用模式，探讨了半圆柱涡对摆动水翼推进性能的影响。

2 数值计算模型

如图1所示，半圆柱通过沿y轴升沉运动产生旋涡。半圆柱振动满足的运动规律可以表示为：

式中：Ad为半圆柱升沉运动的振幅，f为半圆柱的运动频率。

如图1所示，二维摆动水翼既沿着y轴升沉又绕着水翼首缘点摇摆。因此水翼的摆动运动规律[8]可以表示为：

式中：Af为水翼升沉运动的振幅，θ0为水翼摇摆运动的振幅，f为水翼的运动频率。为了便于计算和分析，取半圆柱的运动频率和水翼的运动频率相等。Φ0为水翼升沉运动和摇摆运动之间的相位差，在本文中 Φ0=-π/2。

图1 半圆柱和水翼的周期性运动Fig.1 The cycle motion of an oscillating semicircular and a flapping hydrofoil

摆动水翼的推力系数Cx，侧向力系数Cy和以水翼首缘点为作用点的力矩系数Cm由相应的推力Cx、侧向力Cy和力矩Cm沿水翼表面积分[9]确定：

式中：C0表示水翼的特征弦长，ρ是水的密度，V0为无穷远处来流速度。

摆动水翼的推进效率[10]表示为：

式中：Cxm为推力系数Cx在一个周期内的平均值。

输入功率系数表示为：

3 数值计算方法

3.1 控制方程

对于不可压缩的粘性流动，在笛卡尔坐标系下，用张量的形式表示的时均连续性方程和RANS方程可以写为：

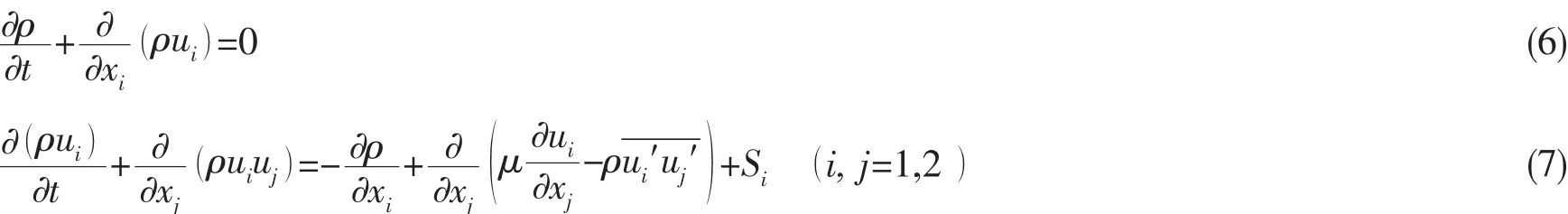
式中：ui为速度分量的时均值，ui′为速度分量的脉动值为速度分量乘积的时间平均值。μ为流体的动力粘性系数。

计算中采用的2方程湍流模型为k-ω SST模型。

在数值求解过程中，采用二维非结构三角形网格划分整个流体域，并采用动网格技术[11]保证物体运动时的网格质量。如图2所示，为了满足计算的精确度，网格在半圆柱和水翼周围分布较密。

图2 计算网格Fig.2 The mesh grid around semicircular cylinder and foil

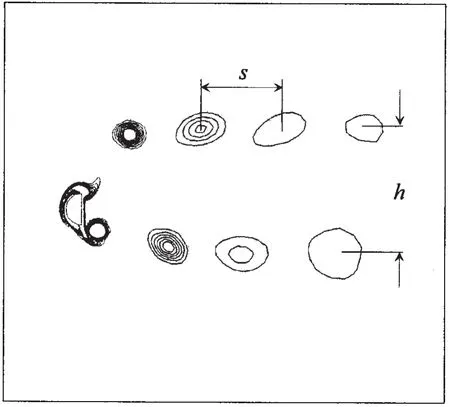
图3 半圆柱振动产生的旋涡Fig.3 The vortices generated by an oscillating semicircular cylinder

3.2 数值计算方法对半圆柱振动问题有效性的验证

如图3所示，半圆柱在振动过程中不断有旋涡脱落到尾流中，随着旋涡向下游移动，涡强不断减弱。这些旋涡类似于卡门涡街，在半圆柱尾流场中形成两排反向旋转，排列有序的涡列。这些旋涡与卡门涡街的不同之处在于两排反向旋转的涡列并不交错。这两排涡列在向下游移动的过程中，在与半圆柱直径平行的方向上总保持一定的距离。计算结果中的现象与Simmons等人的试验[12]相吻合。在计算过程中，尾流场中的脱落涡在距半圆柱8倍直径的范围内可以保持很好的形状和涡强。摆动水翼总是在这一范围内运动，因此选择半圆柱在数值计算中作为旋涡发生装置是可行的。

采用前面提到的数值方法对半圆柱在不同振幅下的水动力性能进行了计算。为了便于分析计算结果，引入了几个无因次参数。a=2Ad/d表示半圆柱的无因次振幅，d为半圆柱的直径。S=s/V0/T、H=h/d分别表示同向旋转的半圆柱涡之间的无因次距离和反向旋转的半圆柱涡之间的无因次距离。如图3所示，其中s为同向旋转的半圆柱涡之间的实际距离，h为反向旋转的半圆柱涡之间的实际距离，T为运动周期。

为验证数值计算方法对于半圆柱振动问题的有效性。对运动参数为f=0.5、V0=2.28 cm/s、d=1.91 cm及a分别取1.0、2.0和3.0这三种工况进行了计算。并与麻省理工学院的实验结果[13]进行了比较。比较结果如图4-6所示，计算与实验符合良好。同时对V0=1.41 cm/s的工况也进行了计算，结果与V0=2.28 cm/s工况近似。

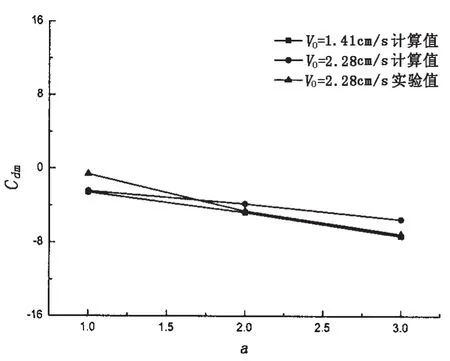
图4 半圆柱平均阻力比较Fig.4 The comparison of the mean drag force coefficient for an oscillating semicircular cylinder between computational and experimental results

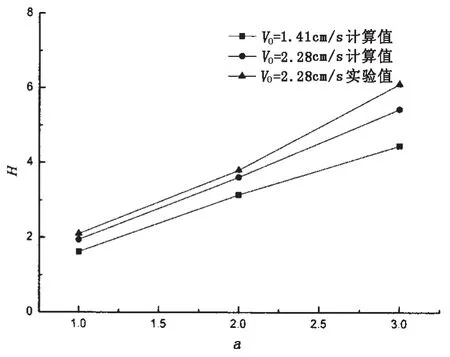
图5 反向旋转半圆柱涡无因次距离的比较Fig.5 The comparison of the dimensionless space for vortices in opposite directions between computational and experimental results

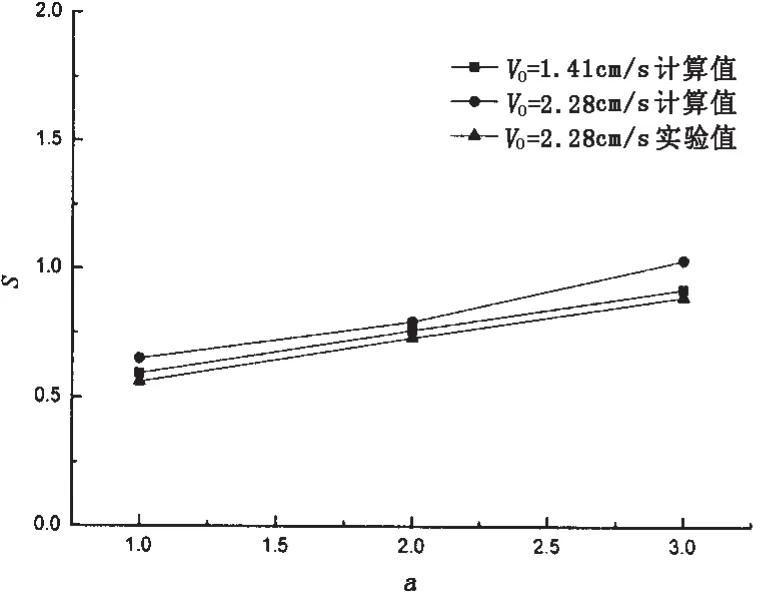
图6 同向旋转圆柱涡无因次距离的比较Fig.6 The comparison of the dimensionless space for vortices in the same direction between computational and experimental results

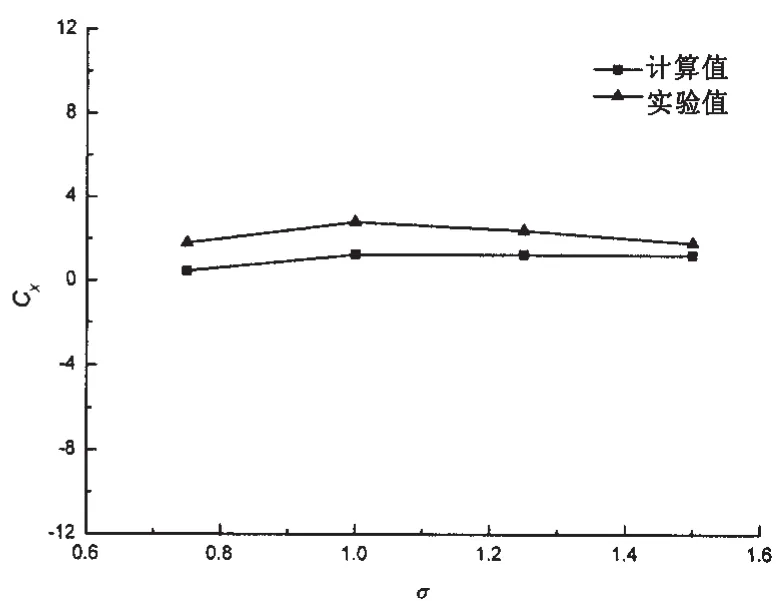
图7 摆动水翼平均推力系数的比较Fig.7 The comparison of the mean thrust force of a flapping foil in the wake of an oscillating semicircular cylinder between computational and experimental results

3.3 数值计算方法对半圆柱水翼串列运动问题有效性的验证

在水翼运动过程中，首缘和尾缘都存在涡量的集中，从而产生旋涡。当水翼在振动半圆柱尾流中运动时，水翼涡和半圆柱涡相互作用。在计算过程中，通过调整水翼到半圆柱的距离改变水翼涡和半圆柱涡的相互作用模式。圆柱中心和水翼首缘之间的距离表示成无量纲数为σ=l/V0/T，其中l为圆柱中心和水翼首缘之间的实际距离。

为了验证数值计算方法对半圆柱和水翼串列运动问题的有效性和精确性。对运动参数为f=0.5、V0=1.41cm/s、d=1.91cm、d/C0=0.5、a=2.0、Ad=Af=d、θ0=15°及 σ 分别取 0.75、1.0、1.25 和 1.5 这 4 种工况进行计算。并与麻省理工学院的试验结果[13]进行了比较。比较结果如图7所示，计算与试验结果的变化趋势基本一致。计算过程中对试验环境的忽略是造成与试验结果偏差的主要原因。

4 数值计算结果与分析

本文对运动参数为 f=0.5、V0=1.41 cm/s、d=1.91 cm、d/C0=0.5、a=2.0、Ad=Af=d 及 σ 分别取 0.75、1.0、1.25、1.5和 2.0，水翼摇摆振幅分别取 θ0=15°和 θ0=30°这 10种工况进行了计算。

4.1 旋涡相互作用模式

在水翼上、下表面，半圆柱涡和水翼涡的相互作用模式如表1所示。在计算结果中，半圆柱涡和水翼涡存在4种相互作用模式，这4种旋涡作用模式在其他学者的试验[14-15]中也有所体现。

表1 旋涡作用模式Tab.1 Modes of action between vortices

模式1：半圆柱涡在向下游移动过程中与水翼涡保持较远距离，半圆柱涡与水翼涡相互影响较小。如图8（a）所示，一个旋涡从半圆柱下方脱落。如图8（b）-8（d）所示，该旋涡在向下游移动过程中，强度不断减弱，直至消失，在这一过程中半圆柱涡几乎没有和水翼涡相互作用。

模式2：半圆柱涡与旋向相同的水翼首缘涡相互作用，并且沿着水翼表面独立地向下游移动。最终半圆柱涡和水翼首缘涡相继融入水翼尾缘涡中。如图9（a）所示，一个半圆柱涡靠近水翼。在图9（b）中，该半圆柱涡和水翼下方的首缘涡相互作用。如图9（c）-9（d）所示，半圆柱涡和首缘涡沿水翼表面向水翼尾缘移动，并最终融入水翼尾缘涡中，随着尾缘涡脱落。

模式3：半圆柱涡在向下游移动的过程中，和水翼首缘涡的相互影响较小，最终融入到相同旋向的水翼尾缘涡中。如图10（a）所示，一个半圆柱涡靠近水翼，与此同时，位于水翼上方的水翼首缘涡产生，并沿水翼表面向水翼尾缘运动。如图10（b）所示，半圆柱涡已经到达水翼的首缘，但此时水翼首缘涡已经融入到了水翼尾缘涡中，因此半圆柱涡并没对水翼首缘涡产生较大影响。如图10（c）-10（d）中，半圆柱涡融入到水翼尾缘涡中,最终随尾缘涡脱落。

模式4：半圆柱涡和相反旋向的水翼涡相互作用。如图11（a）所示，一个半圆柱涡靠近水翼的首缘。在图11（b）中，半圆柱涡和水翼下方相反旋向的首缘涡相互作用，使首缘涡的强度减弱。如图11（c）所示，半圆柱涡离开水翼表面，水翼首缘涡融入到水翼尾缘涡中。在图11（d）中，水翼尾缘涡脱落，半圆柱涡继续向下游移动。

图8 模式1Fig.8 Mode 1

图9 模式2Fig.9 Mode 2

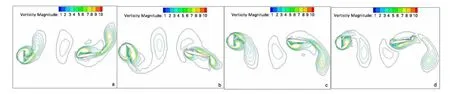
图10 模式3Fig.10 Mode 3

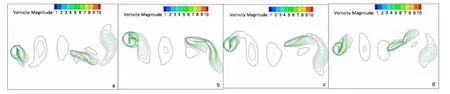
图11 模式4Fig.11 Mode 4

4.2 振动半圆柱尾流中的摆动水翼水动力系数

图12、图13为10种工况下摆动水翼水动力系数在一个运动周期内随时间变化的曲线。如文中所述，在这10种工况中存在多种旋涡作用模式，尽管同种水动力系数曲线的形状相差都不大，但是曲线的幅度变化很大。这说明半圆柱涡对水动力系数随时间变化规律的影响很小，但对水动力系数幅值的影响很大。在一个周期内，推力系数Cx连续变化两次，存在两个峰值，第一个峰值出现在二分之一周期附近，第二个峰值出现在周期结束处。侧向力系数Cy在一个周期内连续变化一次，存在两个大小相等，方向相反的峰值，第一个峰值出现在二分之一周期处，第二个峰值出现在周期结束处。力矩系数Cm的变化规律和侧向力系数Cy的变化规律相似，只是与Cy相比，Cm的幅值要小很多。当σ=2.0时半圆柱涡和水翼涡的相互作用很弱（模式1），因此半圆柱涡对水翼水动力系数的影响很小。如图12所示，在θ0=15°时的水动力系数曲线中，当σ取1.0、1.25和1.5时，水动力曲线的幅值都大于σ=2.0时的幅值。σ=0.75时的水动力曲线幅值小于σ=2.0时的幅值。如图13所示，在θ0=30°时的水动力系数曲线中，当σ取1.25、1.5时，水动力曲线的幅值都大于σ=2.0时的幅值。当σ取0.75、1.0时，水动力曲线的幅值都小于σ=2.0时的幅值。

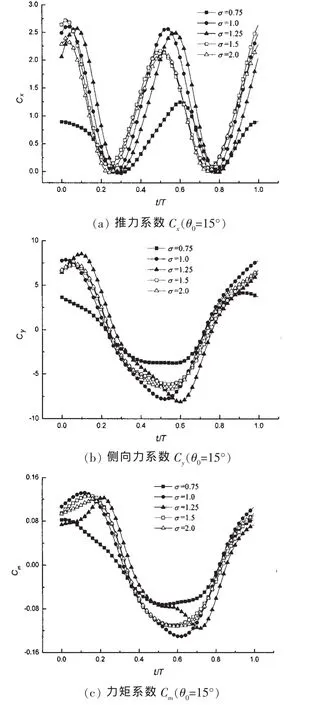
图12 摆动水翼水动力系数（θ0=15°）Fig.12 The hydrodynamic coefficients of a flapping hydrofoil at θ0=15°behind an oscillating semicircular cylinder

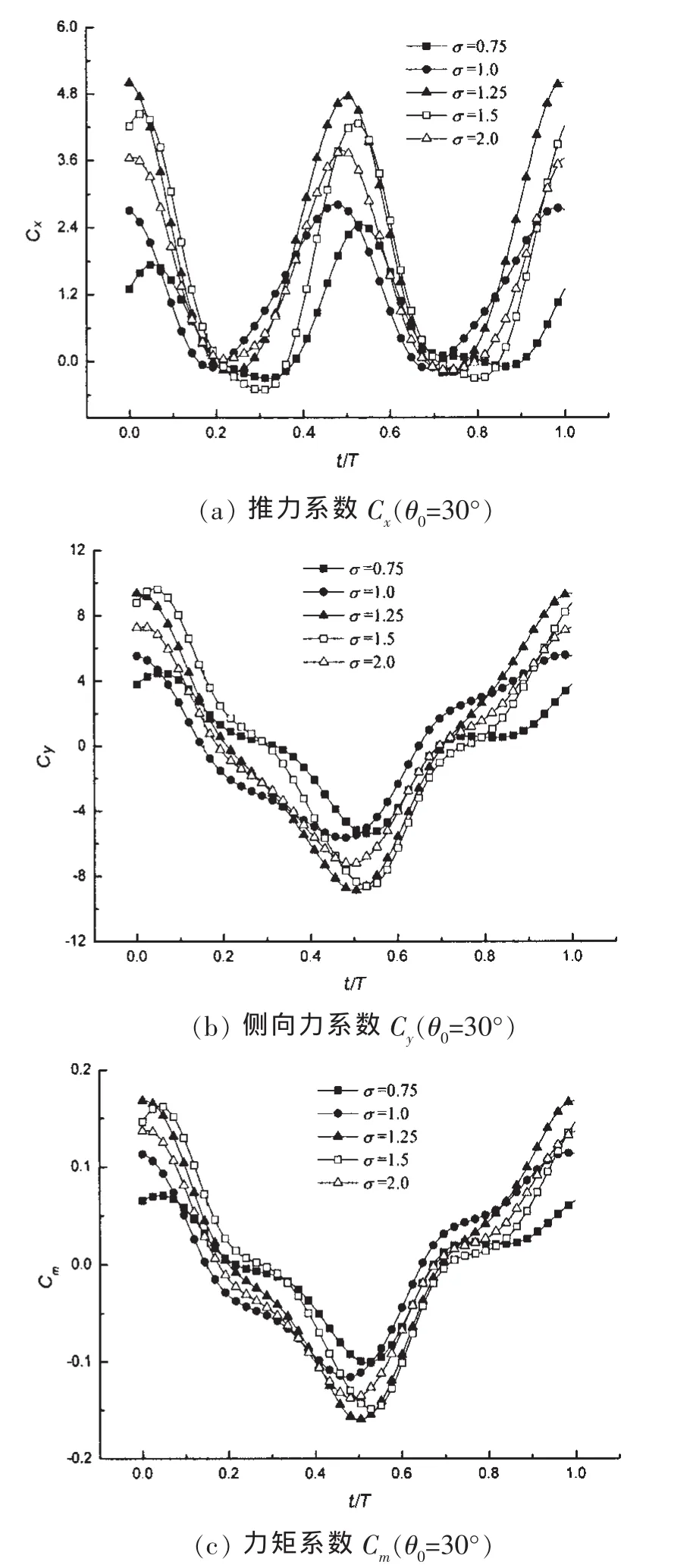
图13 摆动水翼水动力系数（θ0=30°）Fig.13 The hydrodynamic coefficients of a flapping hydrofoil at θ0=30°behind an oscillating semicircular cylinder

4.3 振动半圆柱尾流中的摆动水翼平均推力系数

图14为振动半圆柱后摆动水翼在θ0=15°、θ0=30°时的平均推力系数曲线。当θ0=15°时，最大平均推力系数Cxm出现在σ=1.25时，比σ=2.0时的Cxm高出约10.8%，半圆柱涡和水翼涡以模式4相互作用。当θ0=30°，最大平均推力系数Cxm=2.02出现在σ=1.25时，比σ=2.0时的Cxm高出约34.7%，半圆柱涡和水翼涡以模式4相互作用。综上所述，在计算的10种工况中，最大平均推力系数总是发生在σ=1.25时，此时半圆柱涡和相反旋向的水翼涡相互作用（模式4）。

4.4 振动半圆柱尾流中摆动水翼的输入功率系数和效率

图15为振动半圆柱后方二维摆动水翼在θ0=15°和θ0=30°时的输入功率系数曲线和推进效率曲线。当σ=2.0时，半圆柱涡和水翼涡相互作用很小，半圆柱涡对水翼的输入功率和效率的影响不大。

如图 15（a）所示，σ=1.25时的输入功率系数 Pin比σ=2.0时的Pin高出约17.3%，而σ=1.25时的推进效率η却和σ=2.0时的η接近。这说明水翼在σ=1.25时一部分输入功率并没有输出转化为推力，而是在半圆柱涡的影响下损失了能量。σ=1.5时的Pin与σ=2.0时的Pin接近，但 σ=1.5时的 η比 σ=2.0时的 η 高出约14.3%。这说明水翼在σ=1.5时除了自身运动提供的输入功率外，在半圆柱涡的影响下又额外得到了一部分输入功率，吸收了能量。如图15（b）所示，σ=1.5时的Pin略小于σ=2.0时的Pin，然而σ=1.5时的η比σ=2.0时的η高出约8.1%，这说明σ=1.5时摆动水翼在半圆柱涡的影响下得到额外的输入功率，吸收了能量。

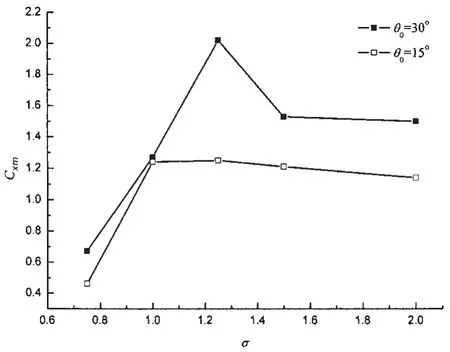
图14 摆动水翼平均推力系数Fig.14 The mean thrust force coefficient Cxmof a flapping hydrofoil

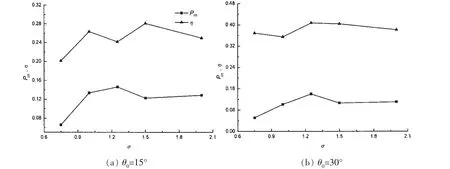
图15 摆动水翼的输入功率系数和推进效率Fig.15 The input power coefficient and propulsive efficiency of a flapping hydrofoil

综上所述，在计算的10种工况中，摆动水翼总是在σ=1.5时吸收能量，此时半圆柱涡和相同旋向的水翼首缘涡相互作用，最终半圆柱涡融入到水翼尾缘涡中（模式2）。

5 结论与展望

本文利用数值方法分析了振动半圆柱尾流中二维摆动水翼的推进性能。计算结果显示振动半圆柱产生的旋涡对摆动水翼的水动力性能有显著的影响。可以得到以下结论：

（1）文中的数值计算方法对于分析半圆柱运动和半圆柱、水翼串列运动都是准确、有效的。

（2）在数值计算中，半圆柱可以作为旋涡发生装置。振动的半圆柱能够产生两排旋向相反、排列整齐和高质量的旋涡序列。

（3）半圆柱涡和水翼涡之间存在4种相互作用模式。半圆柱涡对摆动水翼水动力周期变化规律影响较小，对水动力的幅值影响较大。

（4）摆动水翼最大推力系数出现在旋涡相互作用模式4（旋向相同的半圆柱涡和水翼涡相互作用），摆动水翼从半圆柱涡吸收能量的现象出现在旋涡相互作用模式2（旋向相反的半圆柱涡和水翼首缘涡相互作用，半圆柱涡最终融入水翼尾缘涡）。

振动半圆柱产生的旋涡对柔性摆动水翼推进性能的影响将是下一步研究的方向。

[1]George V Lauder,Eliot G Drucker.Morphology and experimental hydrodynamics of fish fin control surfaces[J].IEEE Journal of Oceanic Engineering,2004,29(3):556-571.

[2]Lindsey C C.Form function and locomotory habits in fish.Fish Physiology[M].New York:Academic Press,1978(7):1-100.

[3]Anderson J M,Kerrebrock P A.The Vorticity Control Unmanned Undersea Vehicle(VCUUV):An autonomous robot tuna[C]//Proceedings of the 11th International Symposium on Unmanned Untethered Submersible Technology.Durham,USA,1999:63-70.

[4]Streitlien K,Triantafyllou G S.Efficient foil propulsion through vortex control[J].AIAA Journal,1996,34(11):2315-2318.

[5]Gopalkrishnan R,Triantafyllou M S,Triantafyllou G S,et al.Active vorticity control in a shear flow using a flapping foil[J].Journal of Fluid Mechanics,1994,27(4):1-21.

[6]Beal D N.Propulsion through wake synchronization using flapping-foil[D].Cambridge:Massachusetts Institutes of Technology,2003.

[7]Zhu Q,Wolfgang M J,Yue D K P,Triantafyllou M S.Three-dimensional flow structures and vorticity control in fish-like swimming[J].Journal of Fluid Mech,2002,468:1-28.

[8]Yan Hui,Su Yumin,Yang Liang.Experimentation of fish swimming based on tracking locomotion locus[J].Journal of Bionic Engineering,2008,5(3):258-263.

[9]Triantafyllou M S,Triantafyllou G S,Yue D K P.Hydrodynamics of fishlike swimming[J].Fluid Mech,2000,32:33-53.

[10]成 巍.仿生水下机器人仿真与控制技术研究[D].哈尔滨:哈尔滨工程大学,2004.

[11]王志东,张晓庆,丛文超.柔性摆动水翼弦向变形模式及其对推进性能影响的研究[J].船舶力学,2010,14(7):609-707.Wang Zhidong,Zhang Xiaoqing,Cong Wenchao.Research on the influence of chordwise deflection mode on the propulsion performance of flexible flapping foil[J].Journal of Ship Mechanics,2010,14(7):609-707.

[12]Simmons J E L.Phase-angle measurements between hot-wire signals in the turbulent wake of a two-dimensional bluff body[J].Journal of Fluid Mechanics,1974,64:599-609.

[13]Anderson J M.Vorticity control for efficiency propulsion[D].Cambridge:Massachusetts Institutes of Technology,1996.

[14]Gopalkrishnan R.Vortex induced forces on oscillating bluff cylinders[D].Cambridge:Massachusetts Institutes of Technology,1994.

[15]Streitlien Knut.Extracting energy form unsteady flow through vortex control[D].Cambridge:Massachusetts Institutes of Technology,1994.