基于EMD－EKF的异步电机效率优化控制研究

，，

（天津理工大学 自动化学院，天津 300384）

1 引言

电能是主要的二次能源，工业和农业生产中大部分的负荷为异步电动机。在工业部门中，超过70%的能量由异步电动机转化为机械能。所以，如果使异步电动机在运行时的效率比现在增加1%，其节能和环境效益也非常可观。异步电动机变频器控制的效率优化可分为建立在损耗模型基础上的损耗控制，最小输入功率控制和简单状态变量的类型［1－5］，对一般动态性能要求不高的恒定频率比例控制设备，如泵，压缩机等采用恒功率因数控制或尽量减少定子电流控制的简单状态变量控制就可以获得良好的节能效果；最小输入功率控制对检测精度要求高算法的收敛时间较长，在优化过程中存在转矩脉动；如果既对驱动系统要求较高效率同时又要求响应速度快（如电动汽车系统），往往采用损耗模型控制策略，在损耗变频驱动系统模型的基础上，以在线优化效率的方法，计算出最佳的磁通为基础的控制策略，这种方法响应速度快，其效率是全局最优解［5］，对于这种方法可靠和准确的获得电机损耗模型和参数信息是获得满意控制性能的重要基础，然而，由于温度和电机铁芯饱和，电机参数在不同运行条件下变化剧烈；此外，由于现代变频调速系统的非正弦电压产生的谐波励磁电流及谐波气隙磁场使转子铁损增加，也会使参数发生变化，影响了效率优化的效果，最优的磁通是几个变量的非线性函数，参数的变化会使其产生很大的变化。在电机参数的估计中，扩展卡尔曼滤波（EKF）是一种常用的方法，该方法使用Taylor级数展开，将非线性滤波问题变为线性滤波问题，但EKF在滤波过程中的假设噪声统计特性是已知的，不确定的噪声统计特性会导致EKF方法得出的均方误差与真实情况有较大的偏差，有时不能准确地反映状态估计的精度。因此，在噪声信息不明的情况下，采用与真实的噪声标准差有较大差异的观测标准差，得出滤波的结果状态并不总是可靠［6］。EMD方法（经验模式分解法）分离信号和噪声，可以用来估计噪声信号中的噪声标准偏差，在观测噪声统计特性不明的情况下［7］，可以先选择观察间隔，在此区间中进行经验模式分解，分离出高频率的噪音进而估计观测噪声的标准偏差，将此标准偏差作为扩展卡尔曼滤波迭代的观测标准差，进行在线参数辨识。基于此种思路，本文将卡尔曼滤波和经验模式分解结合可以有效地提高影响损耗模型参数辨识的精度。

2 效率优化模型

异步电机的电磁时间常数往往远小于其机械时间常数［8］，因此，系统的最小损耗可以在稳态条件下分析，考虑电动机铜损和铁损的总损失模型为［9］

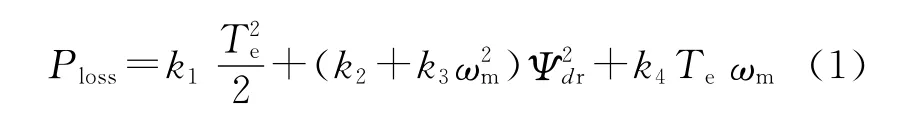
其中

对式（1）求导令其为0就可求得最小损耗对应的磁链，

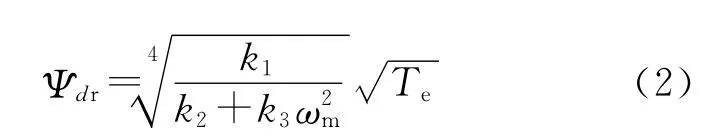
将上述磁链带入式（1），可得到电机最优效率表达式，

电机效率的最优控制取决于电机的参数，其中电机参数变化最大的就是转子电阻Rr，此参数随时间变化缓慢，受电机运行时的温度和速度的影响较大，而且很难准确地用数学表达式来描述。因此，最好的办法是在对Rr进行在线估计，考虑到电机的噪声统计规律的不确定性，使用EMDEKF的方法对非线性变化的参数Rr进行在线估计。

3 EMD方法及其分析

EMD是一个信号分解方法由Huang提出的［10］，将信号在不同尺度的趋势或波动逐级分解，得到具有不同尺度特征数据序列，每个序列被称为本征模态函数（IMF），这种分解可以获得IMF所有的窄带信号，EMD方法是提取数据序列趋势或平均值的最佳途径［11］，EMD方法对每个IMF进行Hilbert变换以获得信号的瞬时频率，IMF的特点是［7］：零点的数量和最大值及最小值的数目相等或最多相差1；最大值及最小值点形成的包络线相对时间轴对称。根据IMF的特点，信号表达式可以写为

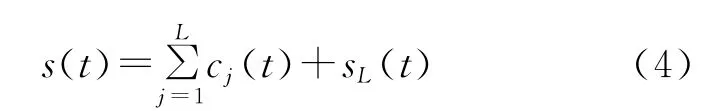
式中：cj（t）为相应的IMF分量；sL（t）为s的残值信号。

EMD的具体方法是：找到所有与原始数据的最大值点和最小值点用插值的办法得到上下包络线，然后，将上下包络线取平均值，得到平均包络线，减去平均包络线后的原始数据序列即为去掉高频信号数据序列，可以分离出没有高频的新数据系列。这样实际是对IMF信号进行低通滤波，得到的低频IMF序列即为低频信号。

4 EMD－EKF方法

EKF实质上是一种随机观察器，它通过非线性动态系统的实时递推来实现最优估计。但EKF最大的不足是要求噪声信号为不相关的白噪声，这一点在实际系统中常常不能满足。

EKF算法过程如下。

设离散系统的m维系统方程和n维测量方程分别为

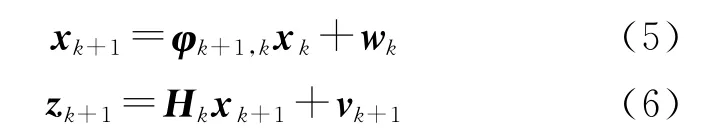
离散卡尔曼滤波器的递推公式如下［12］：

预测估计方程为

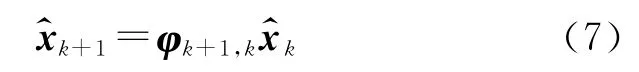
一步预测估计误差为

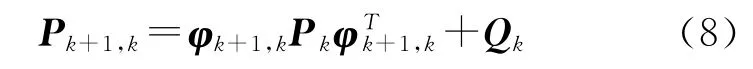
滤波估计方程为

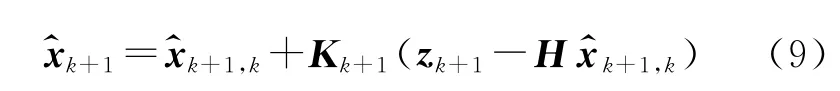
滤波估计误差方差阵为

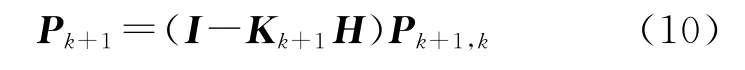
滤波增益为

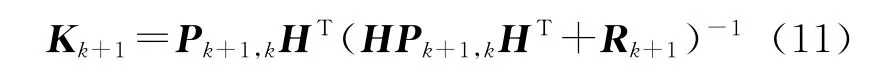
根据IMF的特点，采用对信号s（t）的经验模式分解，具体步骤如下［13］：

1）找到s（t）的所有局部极值点；

2）对极大值点和极小值点，分别建立信号的极大值包络线和极小值包络线，计为emax（t）和emin（t）；

3）在每个时间tk上，计算上包络线和下包络线的均值

4）从输入信号s（tk）中减去均值，得到

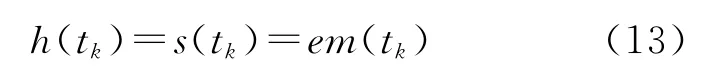
检验h（tk）是否满足IMF的2个特点，若满足则h（tk）应为IMF，如不满足，则用h（tk）代替s（tk），重复步骤1）～4）直到新得到的均值函数em（tk）满足条件：

上述条件满足时，IMF就是由步骤4）得到的最后一个输出函数，计为

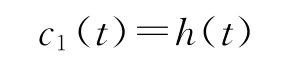
找到c1（t）后，定义s1（t）＝s（t）－c1（t）作为新的输入信号。重复以上步骤得到相应的IMF为c2（t），c3（t），…，cL（t），直到满足停止条件，分解结束，得到最后的残值信号sL（t）。

本文主要是采用EMD方法对未知统计特性的噪声协方差进行估计，而不像传统EKF根据经验人为确定，这样大大提高了估计的准确性，从而使控制系统控制精度得到保证。

5 基于EMD－EKF的效率优化

转子的最佳磁通是一个与工作参数相关的非线性函数，电机参数变化，最佳磁通也会发生变化，其实际控制效果在实践中难以得到保证，特别是转子电阻，在某些情况下，转子电阻会比标称值大1倍以上，参数改变将使运行时转子磁通偏离最优值，导致系统运行不是处在效率最优状态下，甚至可能会增加系统的损耗。为此只能采用参数在线辨识的根本途径来解决这个问题，本文采用EMD方法来估算噪声结合卡尔曼滤波对时变参数估计。考虑到在线实时识别的要求，只对缓慢变化的确定磁链角所必需的转子电阻进行在线估计，以及其他诸如定子电阻，电感和其他参数的变化作为噪声处理，这样不仅能满足实时性要求，同时也提高系统的鲁棒性。图1给出了基于EMDEKF的控制系统框图。

图1 基于EMD－EKF的效率优化框图Fig.1 Efficiency optimization of the control system based on EMD－EKF block diagram

电机在αβ坐标系下的状态方程为［14］

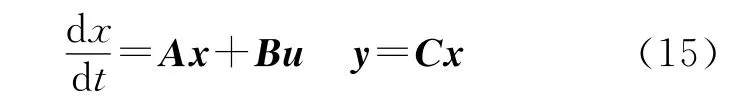
其中

式中：x为状态矢量；u为输入矢量；y为输出矢量。对方程离散化则可得到转子电阻辨识递推算法如下：

1）采用EMD方法估计状态过程噪声协方差阵Qv和状态测量噪声协方差阵Qn，参数过程噪声协方差阵Qw和参数测量噪声协方差阵Qr；

2）初始化状态（0）和状态协方差阵Px（0）和参数（0）和参数协方差阵PRr（0）

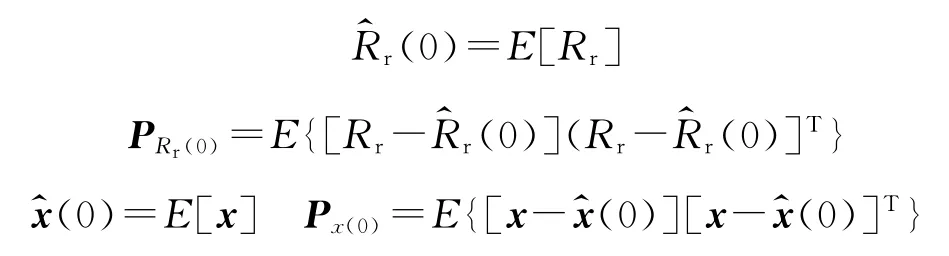
3）在每个采样周期内更新参数滤波方程：

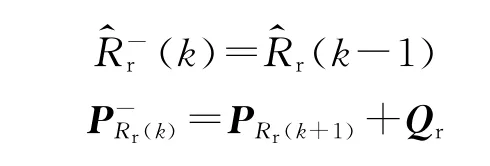
更新状态滤波方程：

更新测量状态方程：

更新测量参数滤波方程：

将辨识出的转子电阻Rr带入到最优磁链表达式（2）就可以得到最优磁链进而控制逆变器输出。

6 仿真和试验研究

为了验证本文提出的控制方案正确性与可行性，本文进行了仿真和试验研究。主要参数如下：额定功率PN＝5.5kW，定子电阻Rs＝2Ω，定子电感Ls＝0.082H，极对数np＝2，转动惯量J＝0.05kg·m2，额定转速nN＝1 500r／min。设dω／dt＝0，因为这些变量相对于电磁参数变化来说是比较慢的。采样周期0.2ms。开始时TL＝10N·m，n＝300r／min，在t＝2.5s时阶跃到TL＝20N·m，n＝400r／min。电磁转矩定子电流，转子电流和转子电阻辨识如图2～图5所示。

从图2～图5可以看出，系统能够很好地跟踪负载的变化，调节时间很短就能够达到稳态。

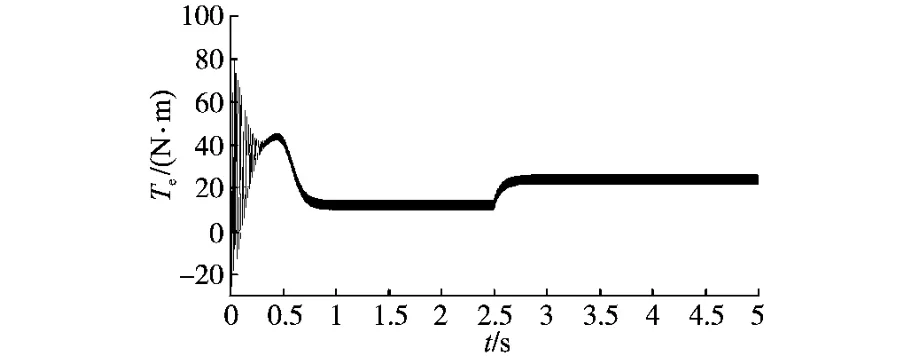
图2 电磁转矩Fig.2 Electromagnetic torque wave

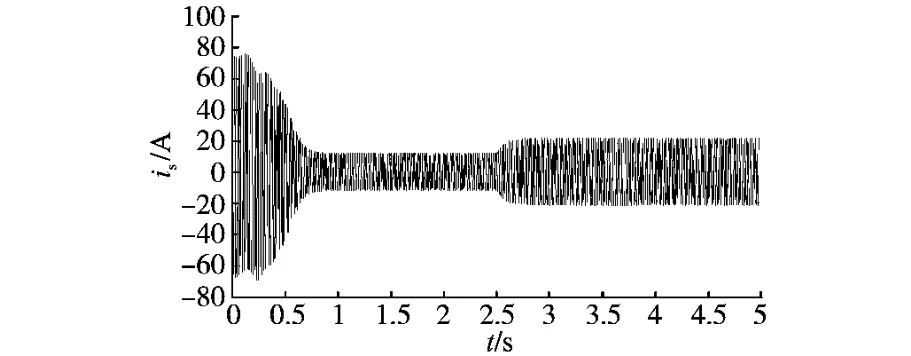
图3 定子电流Fig.3 Stator current wave

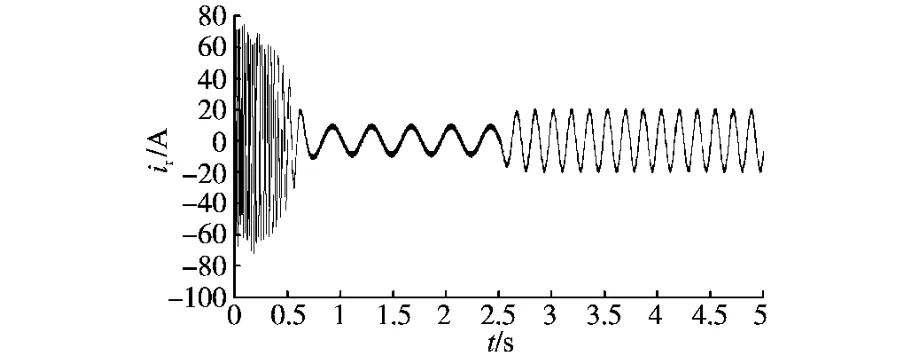
图4 转子电流Fig.4 Rotor current wave

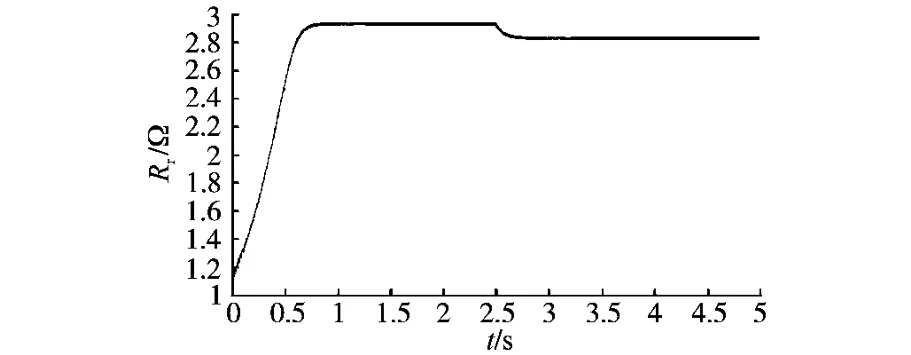
图5 转子电阻辨识曲线Fig.5 Rotor resistance identification

本文还进行了效率对比试验，采用由西门子大功率IGBT SKM400GB176D构成的逆变主电路。采用TI数字信号处理器TMS320F2812及Altera CPLD EPM7128AET100为核心构成控制电路，实现EMD－EKF算法。采用光电码盘来完成速度检测，电流传感器CHB－100S，电压传感器采用CHV－50P。分别采用EKF和EMD－EKF算法对不同负载转矩进行了效率优化对比试验，试验结果对比如图6所示。

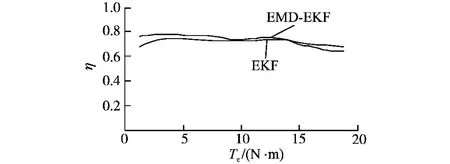
图6 效率优化方案对比图Fig.6 Efficiency optimation scheme comparison

从试验结果可以看出，在负载变化情况下，采用本文提出的优化方法总体上看可以显著地提高系统效率，尤其当负载较轻时效果更为明显。

7 结论

本文针对传统的效率优化方法存在的问题，采用EMD方法结合卡尔曼滤波，有效地利用它们各自的优势，提高估计的精度。然后结合损耗最小化的效率优化方法提出了基于EMD－EKF的异步电机效率优化控制方案。在运行中对变化较大参数进行在线辨识，对控制系统进行优化，最后通过仿真试验验证了方案的可行性和优化算法的有效性。

［1］Ta Cao－Minh，Yoichi Hori.Convergence Improvement of Efficiency－optimization Control of Induction Motor Drives［J］.IEEE Trans.on Industry Applications，2001，37（6）：1746－1753.

［2］Ta Cao－Minh，Chandan Chakraborty，Yoichi Hori.Efficiency Maximization of Induction Motor Drives for Electric Vehicles Based on Actual Measurement of Input Power［C］∥In：The 27th Annual Conference of the IEEE Industrial Electronics Society，2001：1692－1697.

［3］Slobodan N Vukosavic，Levi E.Robust DSP－based Efficiency Optimization of a Variable Speed Induction Motor Drive［J］.IEEE Transactions on Industrial Electronics，2003，50（3）：560－570.

［4］Famouri P，Cathey J J.Loss Minimization Control of an Induction Motor Drive［J］.IEEE Transactions on Industry Applications，1991，27（1）：32－37.

［5］崔纳新，张承慧，孙丰涛.矢量控制异步电动机的效率优化快速响应控制研究［J］.中国电机工程学报，2005，25（11）：118－123.

［6］SHIML，CRATE.Speed Estimation of an Inducton Motor Drive Using an Optimized Extended Kalman Filter［J］.IEEE Trans.on Industry Electronics，2002，49（1）：124－133.

［7］张坤，芮国胜，张洋.EMD－EKF方法研究［J］.海军航空工程学院学报，2010，25（4）：365－368.

［8］Lorenz R D，Yang S M .Efficiency－optimized Flux Trajectories for Closed－cycle Operation of Field－orientation Induction Machine Drives［J］.IEEE Trans.Ind.Applicat.，1992，28（3）：574－580.

［9］刘陵顺，刘卫华，田锦昌.考虑铁损时异步电动机的最佳效率控制［J］.微电机，2001，34（4）：50－53.

［10］Huang N E，Zheng S，Steven R，etal.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proc.R.Soc.Lond.A，1998，454（4）：903－995.

［11］邓拥军，王伟，钱成春，等.EMD方法及 Hilbert变换中边界问题的处理［J］.科学通报，2001，46（3）：257－263.

［12］Joseph J，Lavilola J R.A Comparison of Unscented and Extended Kalman Filtering for Estimating Quaternion Motion［C］∥ The Proceeding of the 2003American Control Conference，2003：2435－2440.

［13］杨世锡，胡劲松，吴昭同，等.旋转机械振动信号基于EMD的希尔伯特变换和小波变换时频分析比较［J］.中国电机工程学报，2003，23（6）：119－121.

［14］陈伯时，陈敏逊.交流调速系统［M］.第2版.北京：机械工业出版社，2005.

［15］杨耕，陈伯时.交流感应电动机无速度传感器的高动态性能控制方法综述［J］.电气传动，2001，31（3）：3－8.