摆动电机的迭代预测及PID控制分析与比较

，

（北京航空航天大学 自动化科学与电气工程学院，北京 100191）

1 引言

摆动电机是近20年来迅速发展起来的一种特殊电动机，在给定的电压下只能在有限转角范围内运动，同时具有直流电机、无刷电机、力矩电机的优点。在有限转角范围内，电机的机械特性和调节特性的线性度好，结构紧凑、效率高、寿命长，能在低速和长期堵转下正常工作。摆动电机主要应用于小转角的高精度控制系统中，如陀螺仪稳定平台、红外成像、瞄准具等，本课题应用于红外扫描系统来驱动平面镜。

传统的伺服控制系统一般由位置环、转速环、电流环等组成，PID控制器不能很好的兼顾动态响应和抗干扰能力的要求，其中积分环节易产生超调，微分环节容易引入噪声，使系统震荡或者失去稳定。而近年来提出的一些新的控制方法如神经网络等，算法较复杂，不利于工程实现。

本文提出并分析一种基于迭代预测算法的位置控制器，特别适用于周期性扫描运动，大大提高了系统的动态特性和跟踪性能。并且控制系统结构简单，易于工程实现，提高了位置控制性能，是一种较为理想的伺服控制方案。

2 有限转角电机模型

有限转角电机采用直流电压控制，磁场由永磁体建立，加电压后定子绕组通过电流产生磁场，与永磁体激磁建立磁场联合励磁使原磁场产生畸变，外磁路磁阻最小位置发生改变［1］。本系统驱动电路部分采用电流控制型，等效为一个一阶延迟环节，在这里只关心电机在有限转角范围内的情况，其驱动特性遵循如下方程：

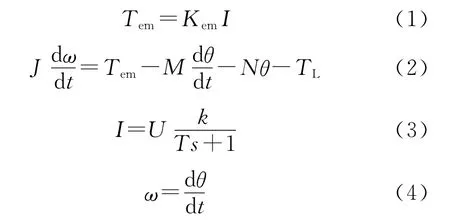
式中：J为转动惯量；ω为机械转速（角速度）；Tem为电磁转矩；TL为负载转矩；I为电枢电流。

式（1）～式（4）做拉普拉斯变换，用Simulink建立电机模型如图1所示［2］。

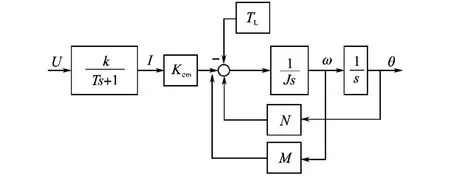
图1 有限转角电机模型Fig.1 The model of limited angle motor

3 状态反馈位置控制器

由式（1）～式（4）得到状态方程为

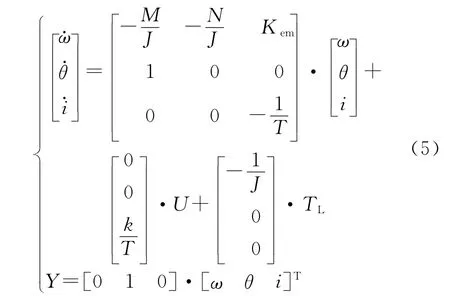
状态方程写为矩阵形式：

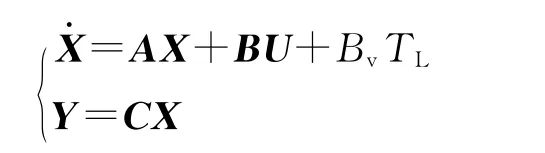
把负载转矩看作扰动，可证明系统可控，观测器输出转子位置可以证明系统可观，输出转子转速也可以证明系统可观，原控制对象的极点分别为s1＝－1.02e4，s2，3＝－102±231i，为了获得良好的快速性以及平稳性，将全状态反馈之后的闭环极点设在s1＝－1.19e4，s2，3＝－1.98e3±1.54e3i。

设状态反馈控制规律为

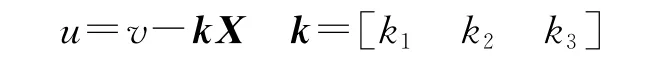
按需求设置极点，通过对比特征多项式系数得出：

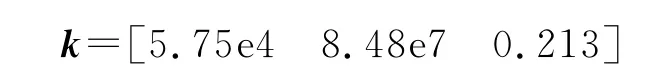
认为负载转矩变化较慢，导数dTL／dt＝0，以转子转速，位置，电枢电流，负载转矩为状态变量写出状态方程为［3］

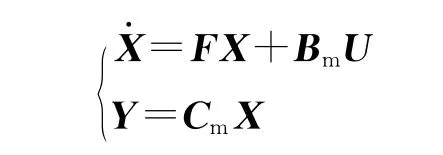
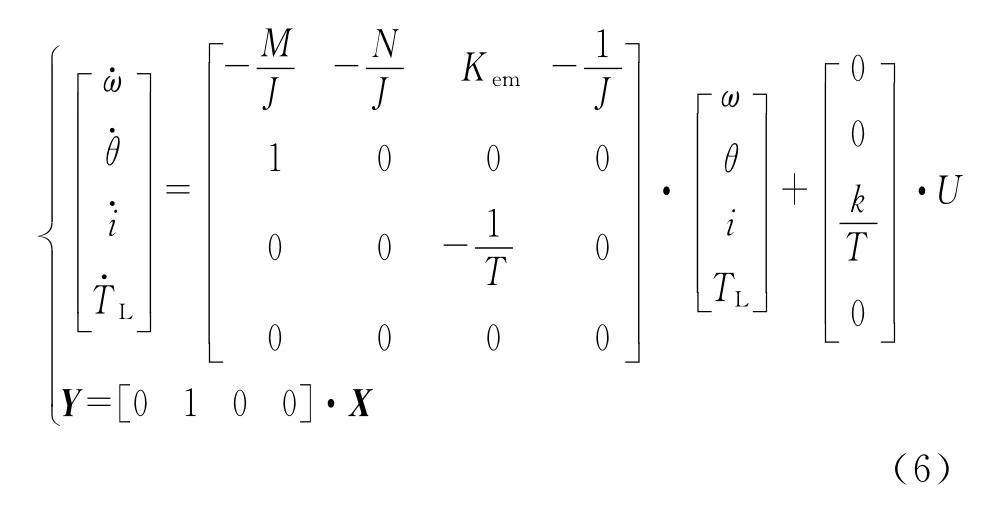
在系统中θ直接由位置传感器给出，故可以降维处理观测器得：

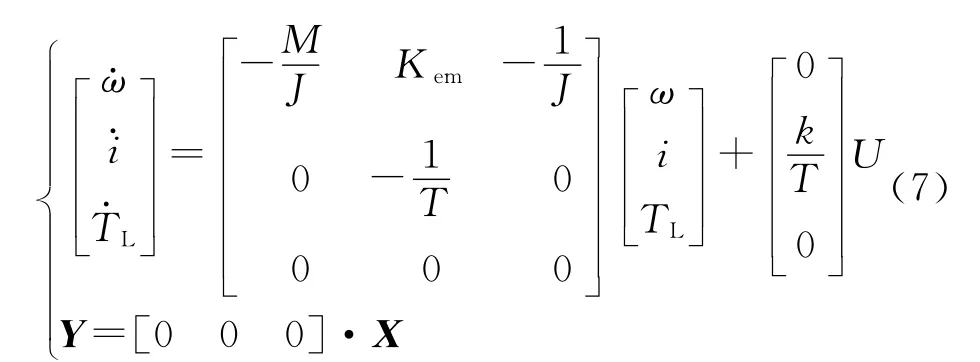
状态观测器方程为

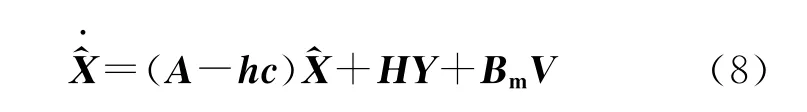
其中以h＝［h1h2h3］T为配置极点，决定状态向量估计误差衰减的速度，将状态观测器极点设置在相比于状态反馈系统极点距离虚轴更远一些的位置，使得观测器响应速度比状态反馈系统响应速度更快。极点设置在s1＝－1.2e4，s2，3＝－2e3±1.6e3i，通过特征多项式系数解出：

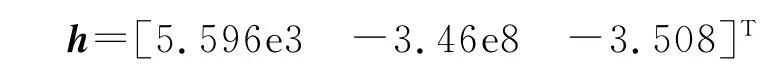
这时系统状态方程写为

假设在转矩观测器收敛后，观测转矩等于实际的负载转矩，为了消除负载转矩的影响，让上式中后两项与转矩有关的量之和为0，可以选择：

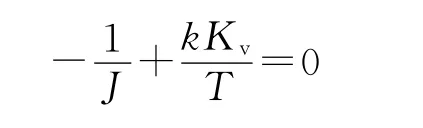
于是得到Kv的值，在负载转矩观测准确时，前馈项可以消除负载变化带给系统的影响，当负载观测存在误差时，误差部分可由比例调节器来补偿［4］。

4 引入迭代预测算法的控制器

本文要解决的是跟踪问题，控制任务是寻找控制u（t）使得输出y（t）在有限的时间区间［0，T］上沿整个期望轨迹实现零误差跟踪，即e（t）＝0，t∈［0，T］，称其为有限时间区间上的完全跟踪问题［5］。

对于重复运行性质的工业过程，具有重复性或者周期性的被控对象，迭代预测算法利用先前的控制经验和测量得到的跟踪误差信号，通过学习率对下一次的控制量进行前馈修正，从而找到一个理想的控制输入，改善控制系统的瞬态性能，实现控制系统的稳态补偿，抑制系统的确定性干扰。基本做法是在反馈控制环的基础上，增加一个迭代预测控制环。迭代预测控制和反馈控制相结合的方式有两种，串联和并联。串联接法中反馈控制器的参考点不断的改变，当该被控系统的模型已知但不精确时，这种接法比较有效。而并联接法中迭代预测控制信号和反馈信号相互叠加到被控对象，又可以分开独立作用于被控对象，且反馈控制对迭代预测控制的收敛性影响不大。另外，迭代预测不依赖于被控系统的详细模型，对于解决非线性问题具有良好的适应性［6］。图2为并联接法迭代学习控制框图。

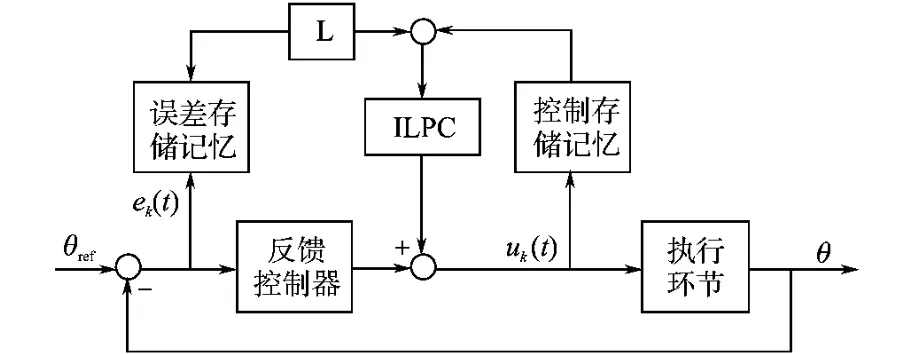
图2 并联接法迭代学习控制框图Fig.2 The parallel connection of iterative predictive control algorithm

迭代算法的基本形式为uk＋1＝uk＋hek。为了减小控制量的剧烈变化，使得系统输出θ到给定值θref，描述t＋d时刻系统输出和期望轨迹之间的接近程度，设性能指标为

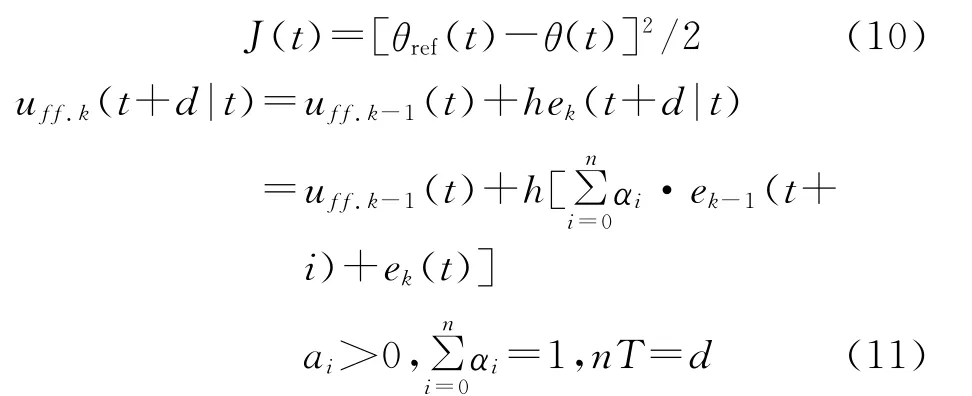
式中，h是迭代矫正系数，h＞0 ，ek（t＋d｜t）＝∑αiek－1（t＋i）＋ek（t）代表未来时刻的未知项，等于前一周期的预测偏差加权滤波项与当前周期偏差的和，起到在迭代学习的基础上预测控制的作用，本质上是使系统提前动作，提高系统跟随性能［5］。

若对于任意的k，ek＋1满足不等式

那么ek＋1将会收敛于一个平衡点，即为迭代学习算法的收敛条件。

根据迭代收敛定理：受控系统和迭代学习算法分别为

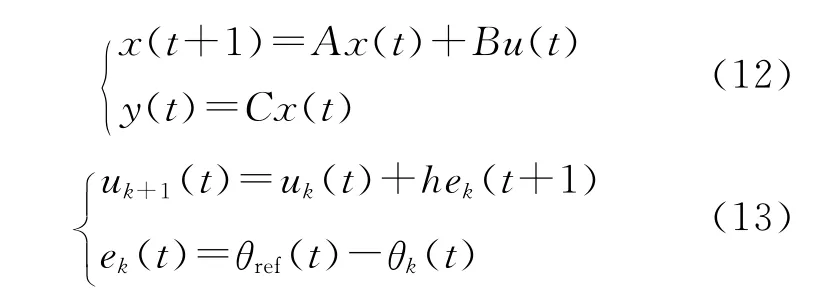
若ρ＝‖I－CBh‖＜1

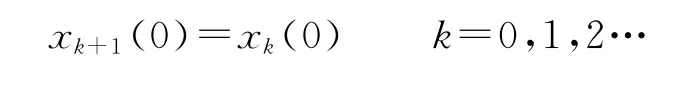
则有

收敛的充分条件为迭代初始值在每次迭代开始时相同，这个条件可以在编写程序时，设置每周期开始时的初始值，从而得到满足。然后就是选择合适的h值使得迭代收敛，具体到本系统采用的迭代公式，由约束条件

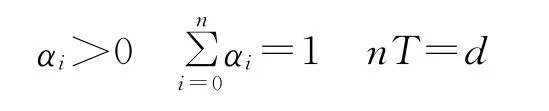
可得：

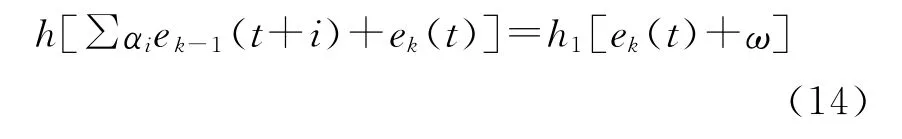
可知h1＝2h，设计得h＝22.5，以及约束条件来设计αi，以达到比较理想的效果。

5 系统仿真结果

在仿真软件Matlab／Simulink平台上进行仿真实验，按照基于状态反馈复合迭代预测控制方法搭建控制部分仿真模型见图3，ILPC为迭代预测控制器，用M函数编程实现。

参考曲线按照项目要求的斜率以及数值设置，周期T＝0.02，正反向扫描比例17∶3，采样时间Ts＝64e－6s，仿真算法选择可变步长，ode45。控制对象部分按照连续模型搭建，控制器部分仿照DSP程序过程按照离散模型搭建。传感器以及DA部分按照理想化搭建，等效为恒定系数［7］。所采用的电机参数为：电机转子转动惯量J1＝4.55e－7kg·m2；Kem＝0.034 26；N＝0.029 1；M＝9.282e－5V／rad／min；T＝9.8e－5，k＝2.51。

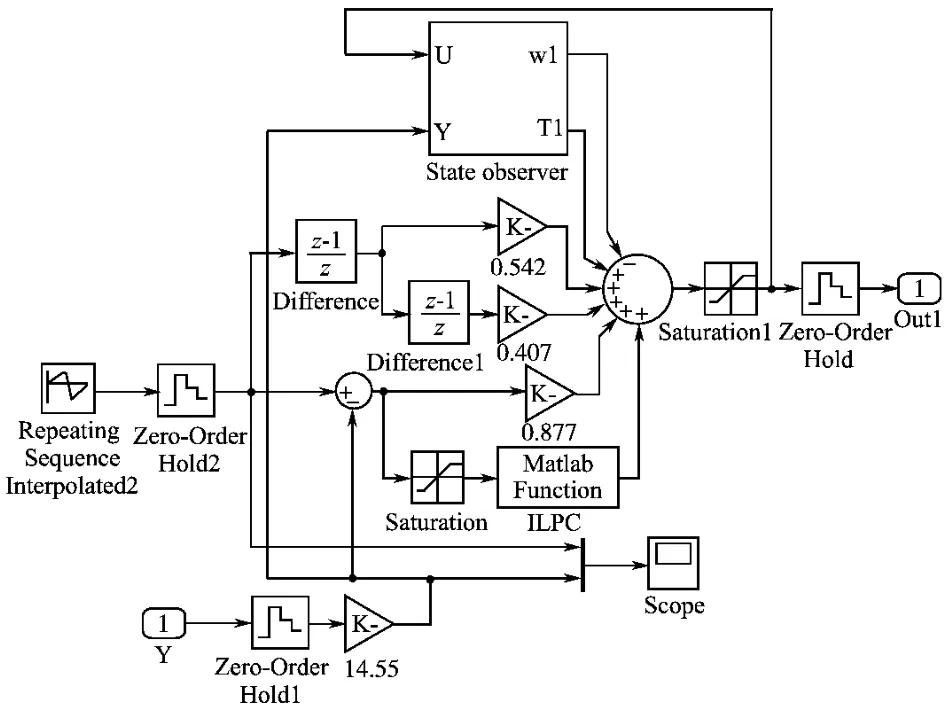
图3 控制系统模型图Fig.3 The model of control system

图4a为传统PID加前馈控制器的仿真结果，可以看出，对于给定轨迹的跟踪效果，电机转子在正向扫描开始处出现小幅的震荡，而且通过调节PID参数无法消除，这对于扫描线性度以及之后的红外成像部分都有较大的影响，这是本系统在精确度要求上所不能容许的，因此传统PID复合前馈控制不能满足系统要求。

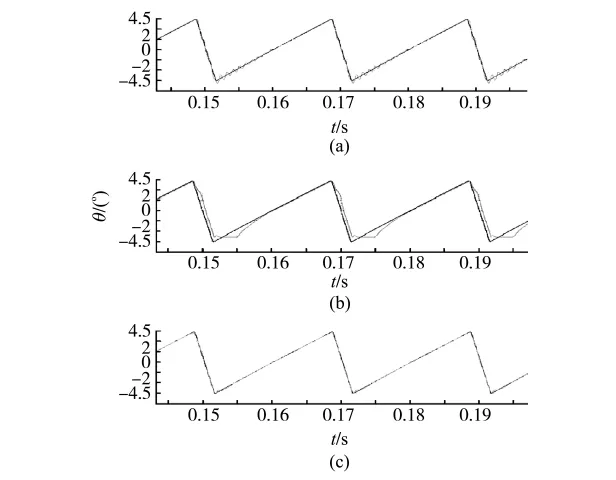
图4 PID控制与迭代预测的波形对比Fig.4 The waveforms of PID and iterative predictive control

图4b中，与传统控制器相比，基于状态反馈以及状态观测器的控制器，正向扫描过程跟随性已经良好，但是，与之前控制策略相同的问题也呈现出来，反向快速回扫阶段接收后，正向扫描过程开始时（即轨迹转折点附近），跟随性能极差，滞后严重，对扫描线性度破坏严重。这个问题是通过调整控制器参数所无法完全解决的。图4c引入前馈补偿的思路，用迭代预测控制器来补偿系统在这一段的性能，可以看到，这时系统在转折点附近的跟随性上升很大，大大提高了扫描线性度区间，达到系统精确度要求。

图5是状态反馈位置控制器加入迭代预测算法前后的仿真对比，可以清楚地看到跟踪轨迹的迭代过程，电机转角在4～5个周期之后达到对预定轨迹的完全跟踪。

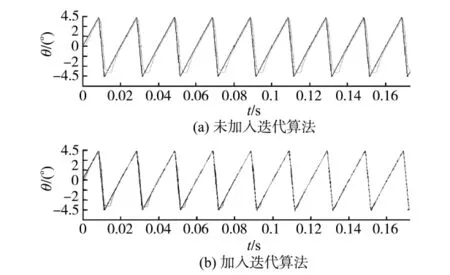
图5 迭代过程仿真波形Fig.5 The waveforms of iterative process

6 实验结果

将控制算法写入DSP中，然后在扫描系统中进行实验并通过测量位置传感器电压得到电机转子的角度，波形记录见图6，波形1即为位置传感器电压，可见电机转子转过的角度与预定轨迹相符合，且精度较高，电机转子做周期性扫描运动，正向扫描以及反向快速回摆过程都比较稳定，波动极小，达到了系统要求。波形2是实测电机电压，从波形可知电压与电机工作过程相符合。由此可知，控制系统在实物实验中能够正常工作，且具有较高精度。

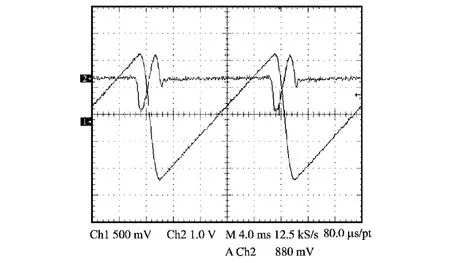
图6 位置传感器及电机电压实验波形Fig.6 The Experiment waveforms of position sensor and motor voltage

7 结论

基于迭代预测算法的位置控制器，控制结构简单，通过仿真及实物实验，可以看到控制器在经过几个周期的迭代过程之后，使得电机转子实现对给定轨迹的零相位跟踪，相比于传统的PID控制器，解决了正向扫描开始处的小幅震荡问题，提高了位置控制精度，且控制器具有更好的抗系统扰动能力，对系统稳定性影响较小，非常适合于扫描伺服系统。

［1］Zhang Y，Smith I R，Kettleborough G.Performance Evaluation for a Limited－angle Torque Motor［J］.IEEE／ASME Transactions on Mechatronics，1999，14（3）：335－339.

［2］赵建辉，田信灵.小角度摆动扫描控制系统的分析与实现［J］.激光与红外工程，2007，36（3）：357－360.

［3］Du Chunyang，Li Tiecai，Cao，Zhengcai.Accurate Tracking Control of a Limited Angle Torque Motor［J］.Electric Machines and Power Systems，1999，27：1191－1199.

［4］王广雄，何朕.控制系统设计［M］.北京：清华大学出版社，2008.

［5］杨磊，周伯昭.高精度摆动扫描技术研究［D］.长沙：国防科技大学，2005.

［6］李志勇.迭代预测控制算法及其应用研究［D］.长沙：中南大学，2006.

［7］于成龙，乔红.基于SIMULINK的扫描电机控制系统仿真［J］.信息与电子工程，2006，4（3）：238－240.