4桥臂APF主电路参数选取方法研究

2012-09-22，，

电气传动 2012年11期

关键词：三相电感矢量

，，

（中国矿业大学信息与电气工程学院，江苏徐州 221008）

1 引言

随着电力电子装置的广泛应用，电网中的谐波问题日益严重，APF作为抑制谐波的有效手段，受到广泛关注［1－3］。APF主电路参数直接影响系统的补偿性能和装置的成本，交流侧电感L与直流侧电容电压Vdc是主电路中2个较为重要的参数。

通常并联型APF通过L与电网相连，电感L起到支撑补偿电流的作用，但目前仍没有统一的方法来选取电感L，许多文献是以已知参数形式给出的，文献［4－7］是在各种假设条件下给出了三相3线制APF电感值的估算方法。

APF直流侧电容电压Vdc主要起支撑直流电压的作用，Vdc越大，系统的补偿效果越好，但成本也就越大，因此应根据实际补偿情况合理选取电容电压值［8－11］。文献［12－14］采用Vdc≥3Em（Em为APF与供电系统连接点的相电压峰值），该方法选取的Vdc较大，使得系统的造价较大。

本文基于三相4线制并联型APF主电路的数学模型，根据补偿电流跟踪性能的要求，计算出L值的取值范围；根据αβγ坐标下的矢量模型，借助于矢量图形分析方法，推导出Vdc选取的临界值。在选取合适主电路参数的基础上，采用了基于广义积分器的空间矢量PWM（3D－SVPWM）控制策略对系统进行补偿。仿真结果表明该参数选取方法的可行性。

2 三相4线制4桥臂APF主电路结构

三相4线制4桥臂APF主电路如图1所示，采用电压型逆变器作为主电路［15］，第4桥臂用来补偿中线电流，此结构解决了三相3线APF不能抑制零序分量的问题，适用范围更广。

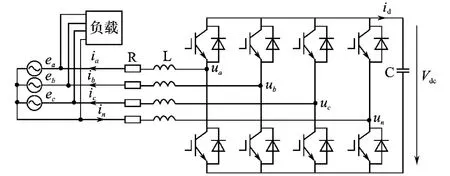
图1 三相4线制4桥臂有源滤波器的主电路结构Fig.1 Main circuit of three－phase four－wire APF with four－leg converter

根据图1写出回路电压方程如下式：

式中：L为交流侧接口电感；R为进线电感等效电阻；ea，eb，ec分别为三相交流电网相电压；ia，ib，ic，in分别为 APF补偿电流，uan，ubn，ucn分别为4桥臂变流器的交流输出电压。

定义Ka，Kb，Kc，Kn为开关函数，其取值为

3 主电路参数设计

3.1 主电路参数关系推导

忽略进线电感的等效电阻，对式（1）进行Clark坐标变换可得

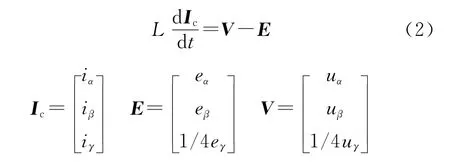
式中：Ic为实际补偿电流矢量。

定义电流跟踪误差矢量为

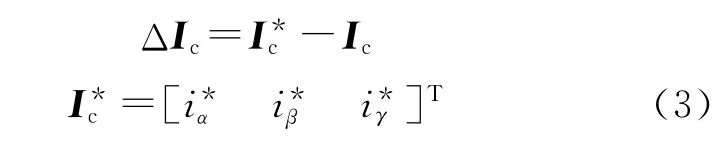
式中：I为参考补偿电流矢量。

将式（3）代入式（2）得：

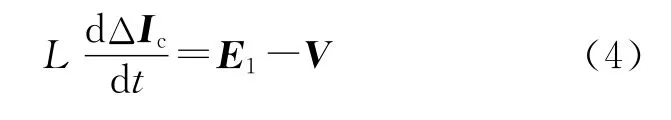
其中

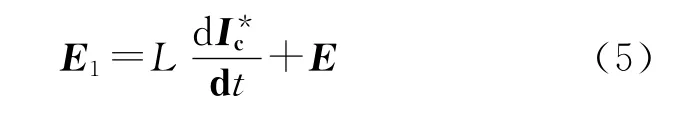
由式（4）可知，ΔIc的变化取决于E1和等效电压矢量V的差值，要保证实际的补偿电流Ic跟随参考电流I＊c，则需要V围绕E1的变化而变化。E1由进线电感L、参考电流I＊c和电网电压矢量E决定，等效电压矢量V的幅值与直流侧电容电压直接相关。可以看出，直流侧电容电压的选取与参考电流I＊c（由被补偿非线性负载决定）、进线电感L和电网电压矢量E密切相关。

采用SVPWM算法等效参考电压矢量时，为了保证参考电压不失真，需要电压矢量在线性调制区。因此，要保证较好的跟踪效果，须满足

即电压矢量E1不能超出变流器基矢量V构成的6棱柱。

3.2 交流侧接口电感值的选取

输出电感L直接决定了补偿电流的跟踪精度［13，16］，选取L时应兼顾补偿电流跟踪能力和抑制补偿电流纹波的要求。下面以A相为例给出具体的参数设计过程。

设A相电压为

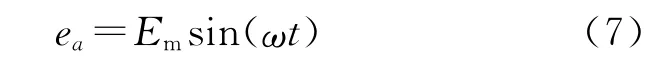
1）满足电流快速跟踪能力时的电感设计。

假设三相电网电压对称平衡，即：

将式（1），式（8）联立求得：

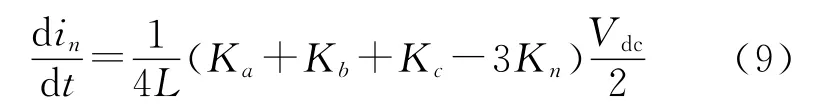
则有：

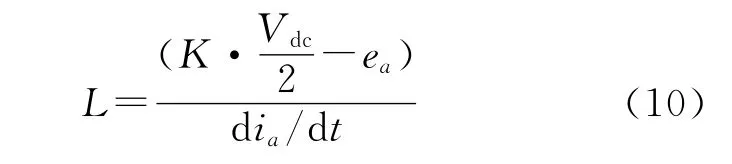
其中

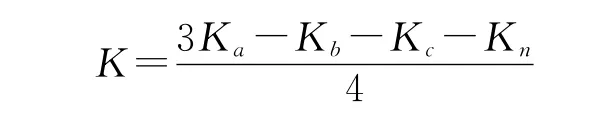
如果APF工作的时间足够长，式（10）中交流电压ea的平均作用将为0。而K取值为1／4的概率是3／7，取值为2／4的概率是3／7，取值为3／4的概率是1／7，因此K的平均取值为3／7。由此可得

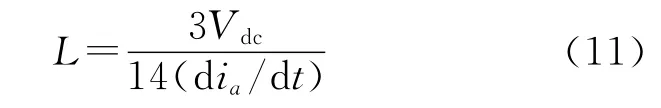
如果APF能跟踪指令电流最大变化率，则需要满足

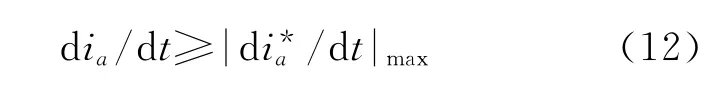
由式（11）、式（12）有

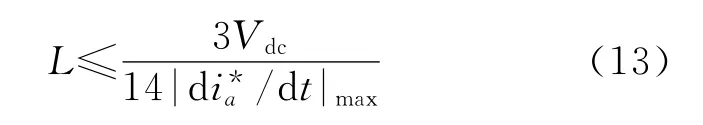
对于不同的负载，指令电流i＊a是不同的，其最大电流变化率与指令电流的具体电流成分是紧密相关的。

2）抑制纹波电流时的电感设计。

假设控制周期为Tc，由式（10）可得：

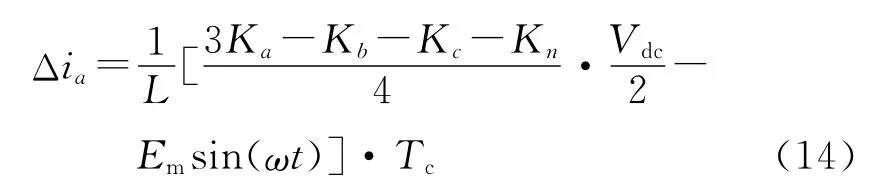
从式（14）可以看出，补偿电流增量Δic与L成反比关系。L过大，则电流增量较小，可能存在局部补偿不到的情况；L过小，则电流增量较大，很难达到纹波要求。因此应折衷选取电感L。

设Δicamax是A相开关周期中允许的最大电流增量，即：

由式（10）可知

得

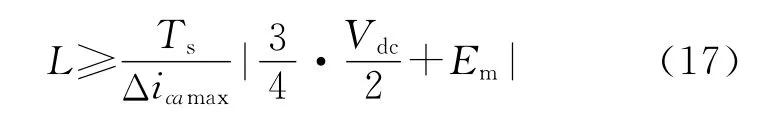
则APF交流侧电感取值范围为

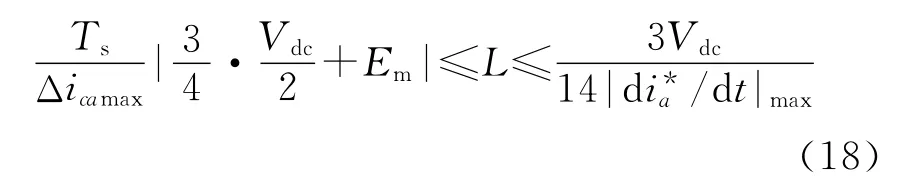
式（18）为电感值提供了选取范围，在实际应用中，需要结合具体的补偿对象和补偿要求进行调整。

4 基于广义积分器3D－SVPWM控制策略

主电路参数选取合理性的验证应以性能较好的电流环跟踪控制策略为前提，本文采用基于广义积分器的3D－SVPWM控制策略［17－18］，如图2所示。

图2 基于广义积分器的3D－SVPWM控制策略Fig.2 3D－SVPWM control strategy based on generalized integrator

图2中ila，ilb，ilc分别为a，b，c三相负载电流，isref，abc为abc坐标系下三相电源参考电流，is，abc为abc坐标系下三相电源实际电流，u为逆变器（VSI）参考电压。

如图3所示，广义积分器与常规积分器的区别在于，它能够实现对正弦参考信号的无静差跟踪。

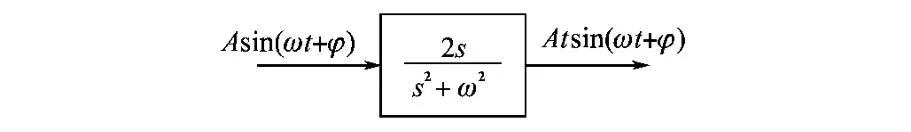
图3 广义积分器Fig.3 Generalized integrator

本文谐波源为三相不控整流桥，特征谐波为6k±1次，通常滤波系统仅需补偿25次以下的谐波成分，即5，7，11，13，17，19，23，25次谐波成分。此时电流控制器如图4所示。

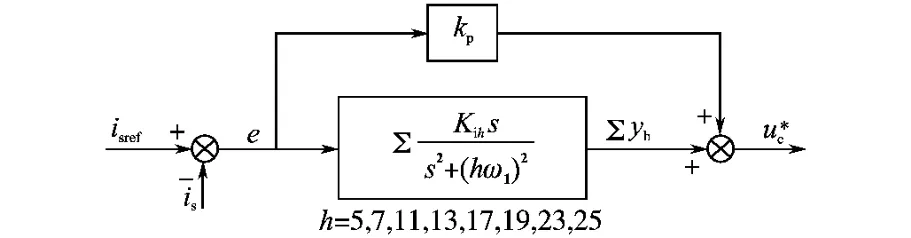
图4 采用广义积分的电流控制器Fig.4 Current controller using generalized integrators

图4中，Kp为比例系数，Kih为广义积分器的系数，h为谐波次数，ω1为基波角频率。

5 设计实例和仿真结果

建立三相4线并联型APF仿真模型［19］，对其进行仿真分析。仿真参数为：电源线电压380 V／50Hz；谐波源为不对称负载，即三相不可控整流桥＋A相电阻负载，如图5所示，整流桥为电阻负载，R1＝60Ω，整流桥交流侧电感L＝0.1mH，A相负载电阻R＝60Ω；主电路的开关频率为5 kHz；谐波电流检测采用d－q法［20］，控制策略采用基于广义积分器的3D－SVPWM策略。

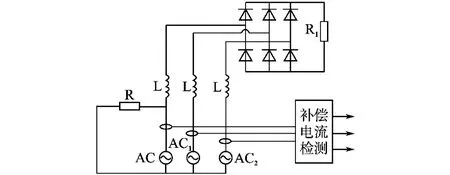
图5 谐波源电路图Fig.5 Figure of harmonic source

负载电流有效值及总畸变率（THD）如表1所示，其25次以下谐波含量如表2所示。根据表2构建谐波源设计主电路参数。

表1 谐波源电流Tab.1 Current of harmonic source

表2 谐波源Tab.2 Harmonic source

假设Δicmax＝40A，由表2的谐波源通过数字仿真计算出｜di＊a／dt｜max，根据式（18）得L的范围为：3.4mH≤L≤10.7mH。

令交流侧电感L＝4.5mH，可得αβγ坐标系下电压矢量E1和逆变器输出电压矢量V的轨迹，如图6所示。

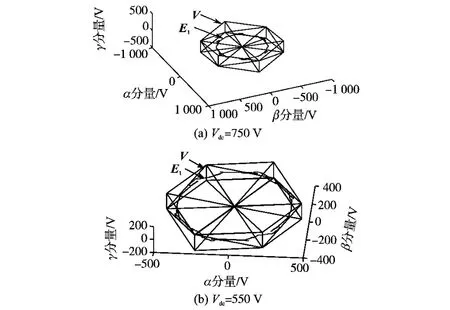
图6 αβγ平面上的电压矢量E1与V（L＝4.5mH）Fig.6 Voltage vectors E1and Vonαβγplane（L＝4.5mH）

取相应参数，补偿后电源电流及频谱见图7。

由绘制的E1与V的矢量轨迹发现，只有当Vdc≥580V时才能够满足式（6）。图6a中Vdc＝750V，E1的轨迹全部在逆变器开关矢量的6棱柱轨迹之内，补偿后的电流波形如图7a所示，电流THD从补偿前19.36%降到3.97%；而图6b中，Vdc＝550V，E1的轨迹不全在6棱柱之内，补偿后电流波形如图7b所示，THD＝8.26%，效果较差。由此可验证Vdc参数选取方法的合理性。令Vdc＝750V一定时，选取合适电感。图8显示不同L时，在αβγ平面内电压矢量E1和逆变器输出电压矢量V的仿真结果。

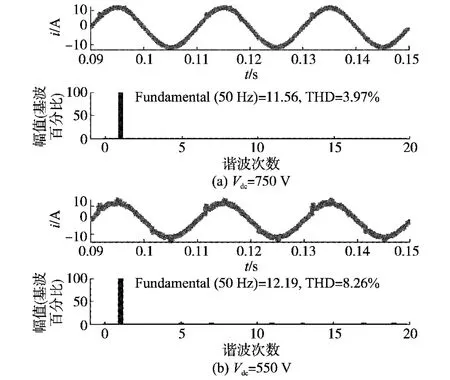
图7 补偿后的电网A相电流波形及FFT分析（L＝4.5mH）Fig.7 A－phase compensated current waveforms and FFT analysis（L＝4.5mH）

图8 αβγ平面上的电压矢量E1与V（Vdc＝750V）Fig.8 Voltage vectors E1and Vonαβγplane（Vdc＝750V）

两种情况下，补偿后的电网电流波形及频谱图如图9所示。

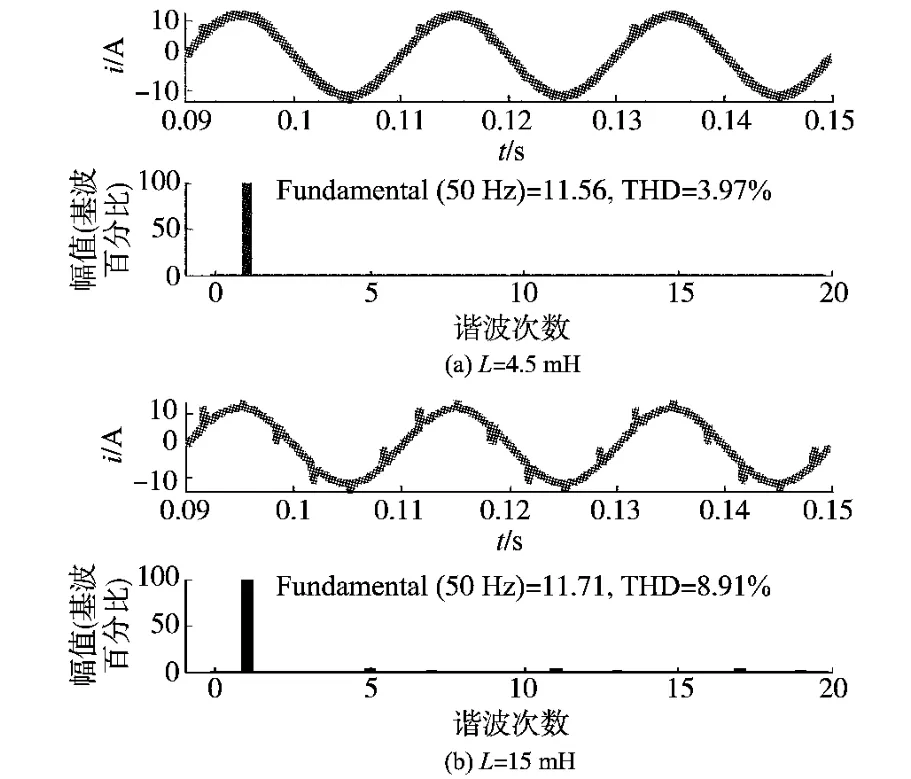
图9 补偿后电网A相电流波形及FFT分析（Vdc＝750V）Fig.9 A－phase compensated current waveforms and FFT analysis（Vdc＝750V）

在Vdc电压值一定的前提下，可以看出，图8a中E1的轨迹全部在逆变器开关矢量的6棱柱轨迹之内，图9a为补偿后电流波形，电流THD从补偿前19.36%降到3.97%，说明此时选用的L值使得APF具有良好的电流跟踪性能，补偿效果较好；而图8b中E1的轨迹不全在6棱柱之内，图9b为补偿后电流波形，THD＝8.91%，效果较差。由此可验证电感参数选取方法的合理性。

结合以上仿真结果可知，根据式（6）、式（13）、式（18）和矢量图分析方法，可快速、合理地确定能够满足补偿性能的电感L、电容电压Vdc的取值范围。表3、表4分别给出了在取值范围内不同参数对应的补偿效果。

表3 不同Vdc时的电源电流畸变率（L＝4.5mH）Tab.3 Supply current distortion rate with different Vdc（L＝4.5mH）

表4 不同L时的电源电流畸变率（Vdc＝750V）Tab.4 Supply current distortion rate with different L （Vdc＝750V）

从表3、表4中可以看出，在L＝4.5mH，Vdc＝750V时，电网电流畸变率为3.97%，补偿效果最好。此时Vdc＜3Em（电源相电压峰值V），在满足补偿要求的同时，又降低了系统成本。

6 结论

本文基于三相4线制4桥臂APF的数学模型，对主电路参数的关系进行了推导，得出主电路各个参数之间是相互联系、相互制约的，不能独立选取。通过Matlab仿真，借助于矢量图分析方法重点研究了交流侧电感L和直流侧电容电压Vdc的选取方法。仿真结果表明了该参数选择方法的有效性与合理性，不仅能够使APF获得良好补偿性能，而且所选参数值比传统方法的选取值小，降低了系统成本。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，2005.

［2］John Stone，Alan Collinson.Power Quality［J］.Power Engineering Journal，2001，5（4）：58－64.

［3］杜雄，周雒维，谢品芳.直流侧APF主电路参数与补偿性能的关系［J］.中国电机工程学报，2004，11（24）：1－4.

［4］Jiang Maoh－chin.Analysis and Design of a Novel Three－phase Active Power Filter［J］.IEEE Transactions on Aerospace and Electronic Systems，2001，37（3）：824－831.

［5］Chaoui Abdelmadjid，Gaubert Jean－Paul.On the Design of Shunt Active Filter for Improving Power Quality［C］∥IEEE International Symposium on Industrial Electronics，2008：2331－2337.

［6］陶俊，刘正之.有源电力滤波器的主电路参数设计［J］.电源技术应用，2001，3（3）：61－64.

［7］侯世英，嵇丽明，索丽娟.改进型直流侧有源电力滤波器参数设计及仿真［J］.重庆大学学报，2009，9（32）：1065－1069.

［8］周雪松，周永兵，马云斌，等.并联型有源电力滤波器直流侧电压分析［J］.中国电力，2009，42（2）：24－29.

［9］周柯，罗安，夏向阳，等.大功率有源滤波器直流侧电容设计与电压控制［J］.电力电子技术，2007，41（4）：12－15.

［10］石峰，查晓明，陈允平.考虑时滞的APF直流侧电容电压波动规律分析［J］.电力电子技术，2008，42（6）：20－22.

［11］陈庆国，赵春明.三相4线制并联型电力有源滤波器的算法和参数仿真［J］.电机与控制学报，2009，13（1）：20－24.

［12］陈伟强.三相4线制有源电力滤波器主电路设计［J］.电气技术，2009，6（16）：12－17.

［13］王聪，李世明.有源电力滤波器设计［J］.电源技术应用，2006，7（9）：21－25.

［14］张国荣，齐国虎，苏建徽，等.并联型有源电力滤波器输出电感选择的新方法［J］.中国电机工程学报，2010，30（6）：22－27.

［15］乐健，姜齐荣，韩英铎.基于统一数学模型的三相4线并联有源电力滤波器的性能分析［J］.中国电机工程学报，2007，27（7）：108－114.

［16］张国荣，赵春柳，丁明，等.输出滤波器对PAPF系统性能影响的仿真分析［J］.系统仿真学报，2009，21（4）：969－972.

［17］王晓刚，谢运祥，帅定新，等.四桥臂逆变器的快速三维SVPWM算法［J］.华南理工大学学报：自然科学版，2009，37（7）：94－99.