考虑软土结构性损伤的柱形孔扩张理论分析

雷华阳 ，丁小冬，张万春

(1. 天津大学 土木工程系，天津 300072；2. 天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072)

1 引 言

管桩在我国的应用越来越广泛，其在承载力、抗弯、抗拔性能方面有显著的优越性。然而管桩施工会引起明显的挤土效应，桩周土体被压密，改变了桩周土体的位移和应力状态[1]，会影响建筑物、地下管线等的正常使用。

随着工程实践的发展，学者们对管桩挤土效应的理论研究也越来越深入。柱形孔扩张理论是分析沉桩对周围土体影响的一种重要方法，Buuterfield等[2]率先将一维平面应变下的柱形孔扩张理论引入沉桩挤土效应的问题中。Vesic[3]进行了弹塑性假定，得到了柱形孔扩张问题的基本解答。由于软土的压缩曲线存在显著的应变软化阶段，因而在推导柱形孔扩张理论时有必要考虑软土的结构性损伤。蒋明镜等[4]（1995）在考虑应变软化的基础上提出了应力一次跌落应变软化模型，得到了不同软化程度对柱形孔扩张时应力场、位移场及塑性区开展规律的影响。姜珂[5]、方万军[6]、孙渝刚[7]采用三折线软化模型，推导了柱形孔扩张问题的理论解答，同时分析了不同因素的影响。

前人对于结构性损伤的考虑集中在应力一次跌落应变软化模型和三折线应变软化模型，本文拟在考虑软土结构性损伤的前提下，采用简化的四折线应变软化模型，通过Mohr-Coulomb屈服准则和相关联流动法则，推导出改进的柱形孔扩张理论计算分析方法，并与前人的研究成果进行对比。

2 应变软化四折线模型

对于柱形孔扩张理论，考虑软土的结构性损伤时，依据结构性软土应变软化的典型应力-应变关系曲线，可通过四折线模型将其分为四个阶段：即弹性阶段OA，此时土体的应力小于峰值应力，应力-应变基本呈线性关系；第1塑性破坏阶段AB，土体的应力达到峰值应力后出现屈服台阶，应力保持不变，应变继续增大；软化阶段 BD，应变增大到一定程度后，应力开始减小，呈应变软化现象；第 2塑性破坏阶段 DE，应力减小到残余应力，达到完全塑性状态，如图1所示。与三折线模型相比，四折线模型多了一个塑性破坏阶段，其应力-应变关系与实际的应力-应变关系更为接近。

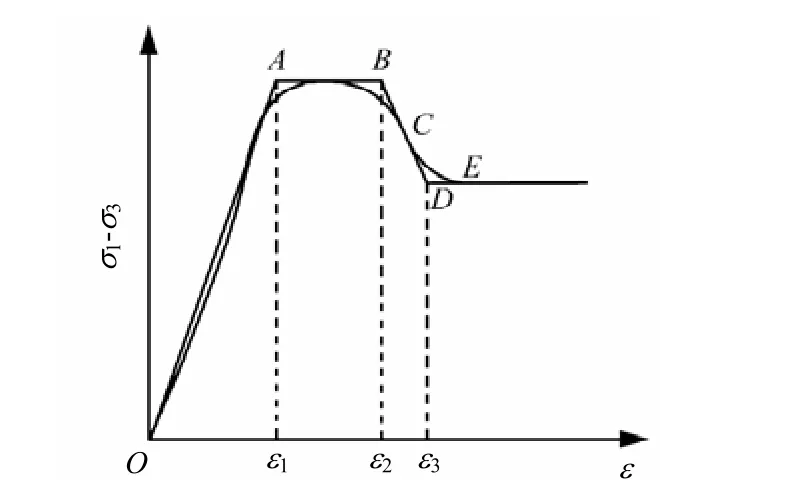
图1 应变软化四折线模型的确定Fig.1 Determination of four-fold line strain softening model

应变软化四折线模型各直线段及其相应参数可通过如下方法获得：对压缩试验曲线的上升段，过原点 O作切线交峰值应力强度处的水平切线于 A点；作曲线下降段拐点C的切线，交峰值强度处的水平切线于点B，交残余强度处点E的延长线于点D，连接上述各点即可得到简化四折线应变软化关系曲线。

假设A点的应变为ε1，B点的应变为ε2，D点的应变为ε3，同时令

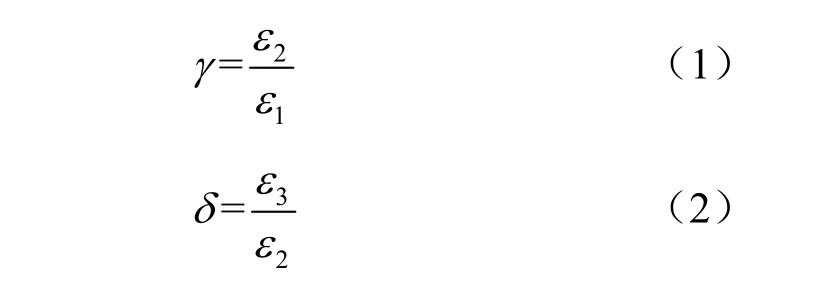
式中：γ为软化区初始阶段应变与第一塑性破坏区结束阶段应变的比值，δ为第二塑性破坏区初始阶段与软化区结束阶段应变的比值。

柱形孔扩张理论中，随着内压力的逐渐增大，孔外介质分为4个区域：弹性区、第1塑性破坏区、软化区和第2塑性破坏区，如图2所示。

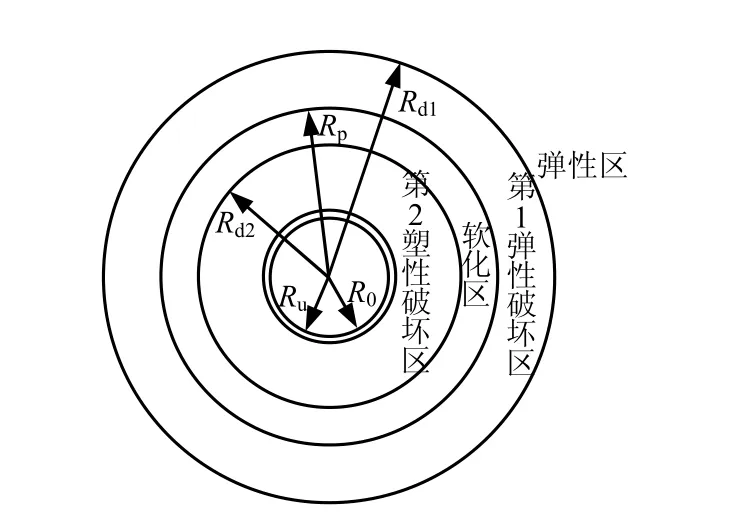
图2 采用四折线应变软化模型时桩周土体的分区Fig.2 Regions around pile using four-fold line strain softening model

变软化四折线模型的基本假定为：（1）土体为均质、各向同性的无限介质；（2）土体具有均布的内压力p0；（3）土体材料屈服服从修正后的相应屈服准则。

采用Mohr-Coulomb屈服准则，当土体开始产生损伤，进入第1塑性破坏状态时，采用第2屈服函数：

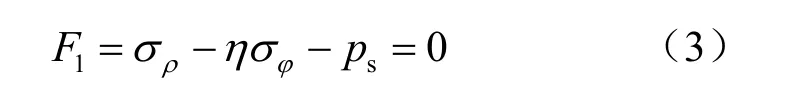
式中：c，φ为土体的初始黏聚力和内摩擦角。

土体进入线性软化阶段时，采用第2屈服函数：

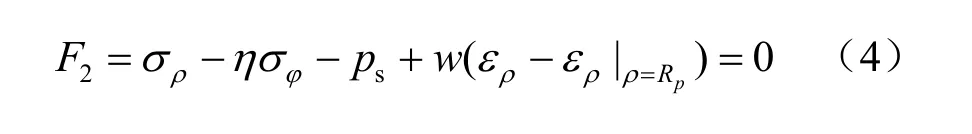
式中：w为软化系数。

土体进入第2塑性破坏阶段时，采用第3屈服函数：

式中：k1、k2为损伤参数，分别为

式中：cr、φr分别为土体的残余黏聚力和残余内摩擦角。

软化阶段和破坏阶段采用非相关联流动法则来考虑土体的剪胀性，分别满足如下公式：

第1塑性破坏阶段：

软化阶段：

第2塑性破坏阶段：

3 柱形孔扩张问题的理论推导

柱形孔扩张问题属于平面应变轴对称问题，可以采用极坐标进行解答，公式推导如下： 平衡微分方程为

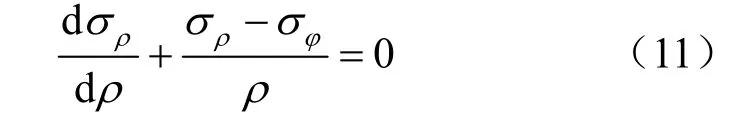
几何方程为

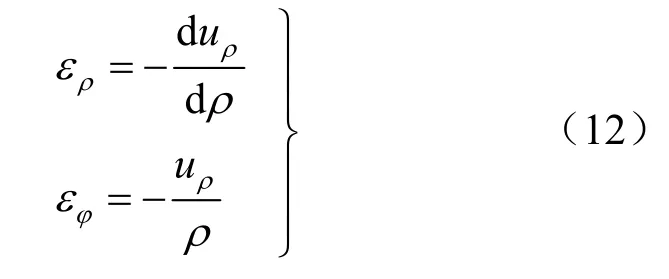
物理方程为

相容方程为：

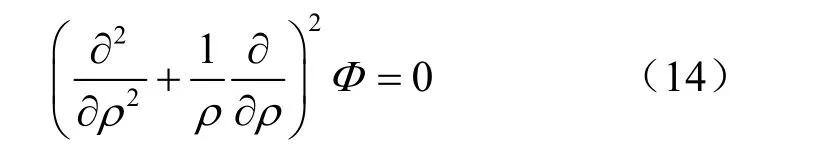
3.1 弹性区解答

根据弹性力学知识，由式（11）～（14），结合柱形孔内表面边界条件 (σρ)ρ=R0= p 可得应力和位移的表达式为

在弹性区De内，考虑土体内初始应力为p0，式（15）可近似化为

由式（16）可近似得到考虑初始应力p0的弹性区位移解为

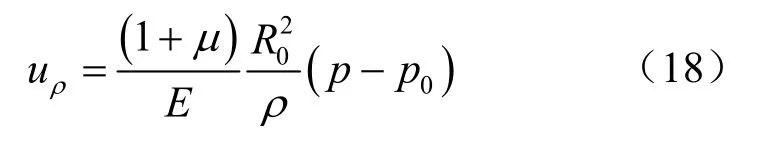
将式（18）代入式（12）可得：

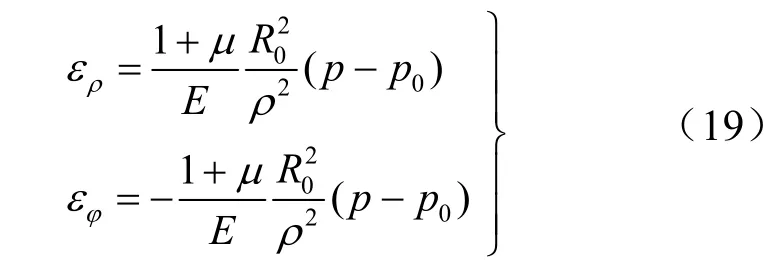
在弹性区和第1塑性破坏区的分界面处，满足第1屈服函数，则可得到分界面处应力和应变分别为

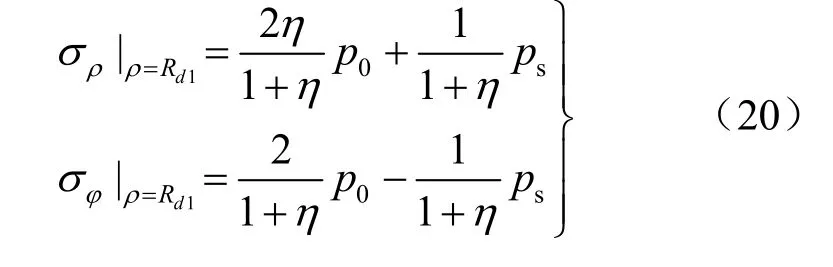
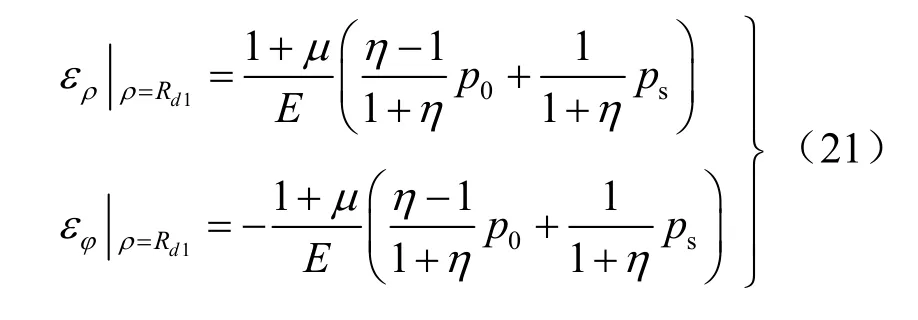
3.2 第1塑性破坏区解答

在第1塑性破坏区内，由式（3）和式（11）可得：

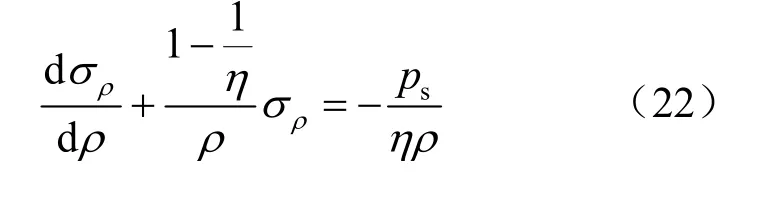
上式为一阶线性非齐次微分方程，由边界条件式（20）可得：

将式（23）代入式（3）可得：

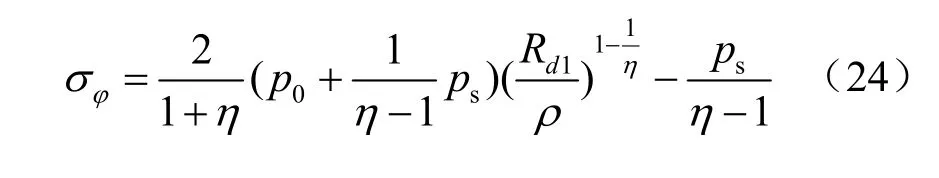
第1塑性破坏区的应变可以表示为

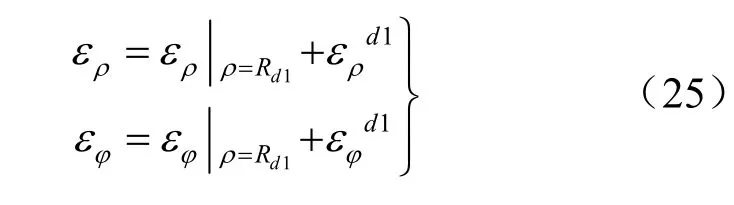
由式（7）、式（12）、式（21）和式（25）可得：

将式（27）代入式（12）可得到应变解为

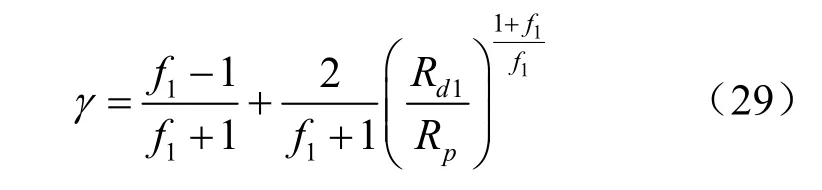
3.3 软化区解答

在软化区内，由塑性增量本构理论可知：

由式（8）、式（12）、式（28）和式（30）可得：

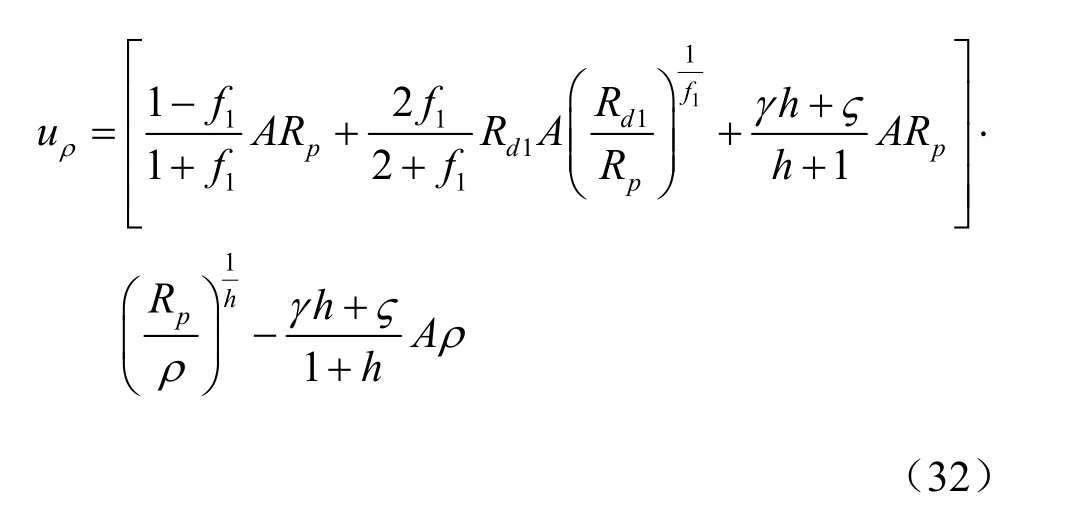
将式（32）代入式（12）得：

将式（28）、式（33）代入式（30）可得：

由式（4）、式（11）和式（34）可得：

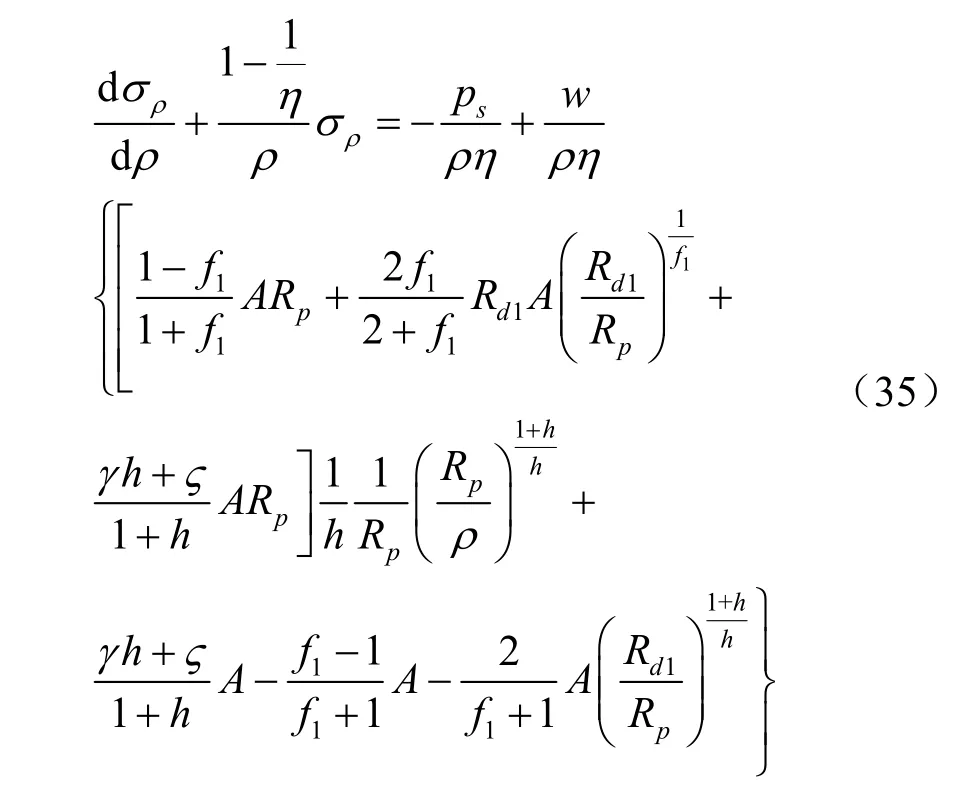
结合第1塑性区应力的边界条件可得：

将式（36）代入式（4）可得：

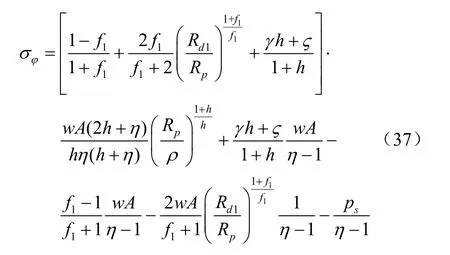
3.4 第2塑性破坏区解答

与软化区的推导过程类似，可得到第2塑性破坏区的位移、应变和应力的计算公式如下：

其中

4 极限扩张半径与极限扩张压力值

采用四折线模型时，柱形孔扩张后体积应满足如下的关系：

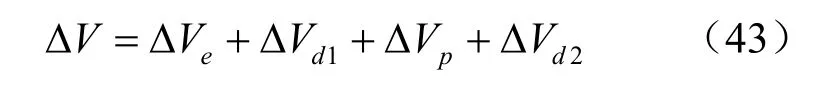
式中：ΔV为扩孔体积变化值；ΔVe为弹性区体积变化值；ΔVd1为第1塑性破坏区体积变化值；ΔVp为软化区体积变化值；ΔVd2为第2塑性破坏区体积变化值。

则可得：

由弹塑性力学知识可知，空间问题的体应变为

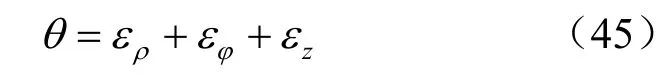
由于柱形孔扩张理论研究的是平面应变问题，则 εz=0，上式可变为

第1塑性破坏区的体积变化值为

由式（28）、（46）和式（47）可知

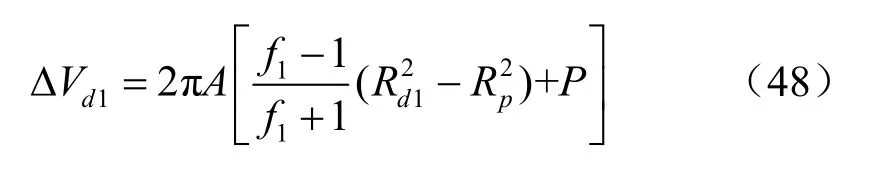
与第1塑性破坏区相似，可得到软化区和第2塑性破坏区的体积变化值分别为

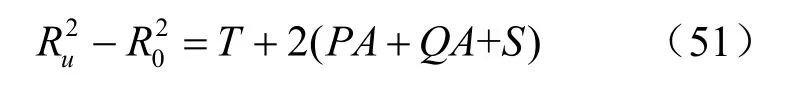
其中

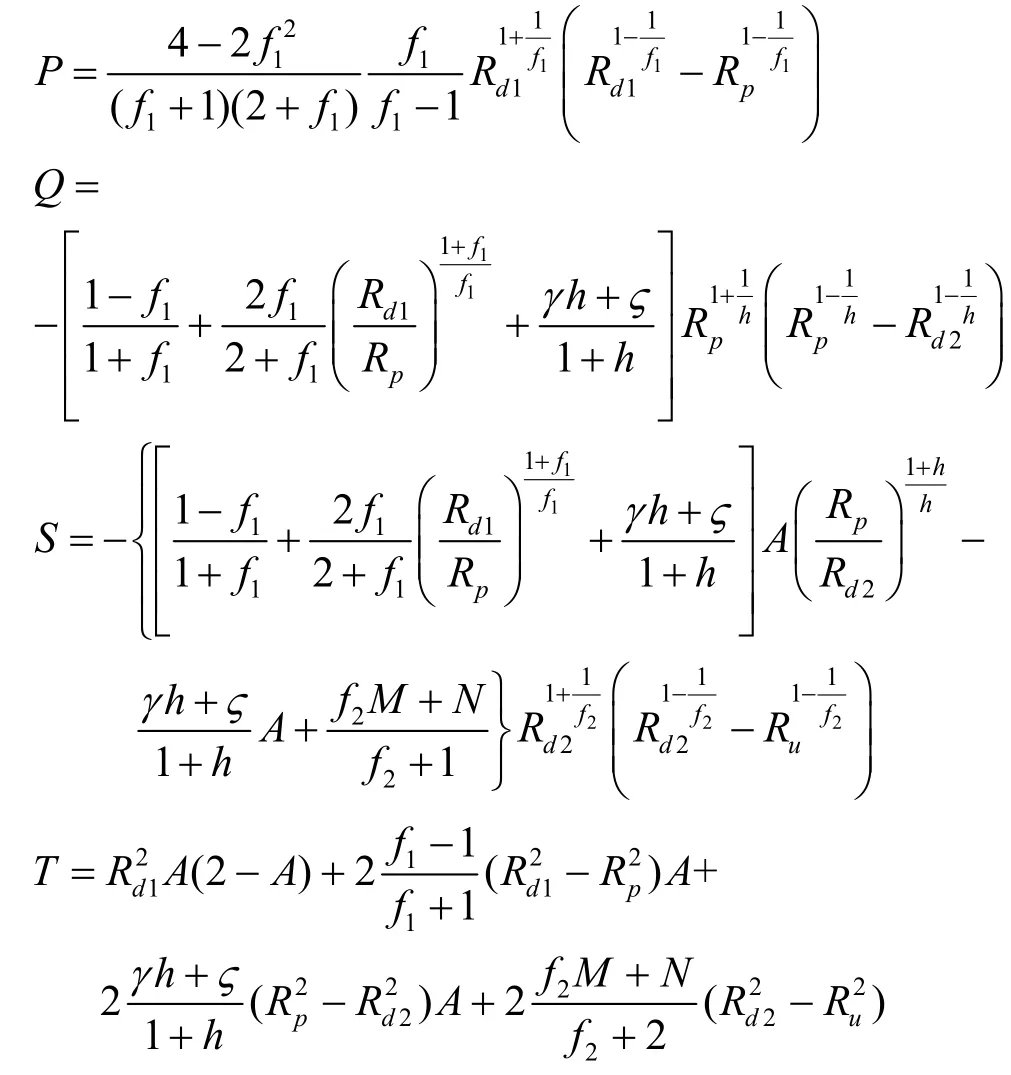
由式（29）、式（38）和式（51）可以求得极限第1塑性破坏区半径Rd1、软化区半径Rp与极限第2塑性破坏区半径Rd2。

由于在软化区与第2塑性破坏区分界面 ρ=Rp处的应力连续，由式（36）和式（41）可得：

由上式可以得到土体的极限扩张压力值为

5 对比分析

为了与不考虑软土结构性损伤的理想弹塑性模型[2]、考虑软土结构性损伤的应力一次跌落应变软化模型[4]及其三折线应变软化模型[8－10]进行对比，依据天津某软土场地 PHC管桩基础工程进行现场测斜监测，测斜点距桩中心的距离为2、4、8 m，监测的深度为 27 m，地下水位埋深为-2.8 m，对10 m深度处土体通过固结不排水三轴试验得到相关参数，用上述四种方法进行塑性半径、软化半径、极限扩张压力及理论水平位移的计算，并与实测位移进行比较，相关土层的物理力学性质见表 1，不同模型的参数见表2。

PHC管桩的外径为0.5 m，假定扩张后的孔径为 0.6 m，通过对四种模型的柱形孔扩张理论进行计算[11]，可得到塑性区半径、软化半径、极限扩张压力及2、4、8 m处的水平位移，见表3。

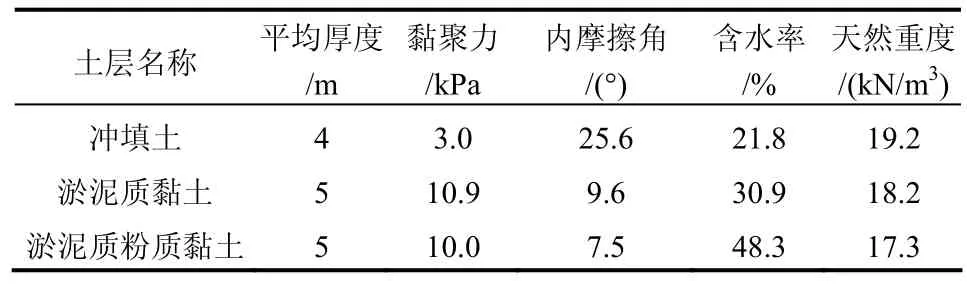
表1 土层物理力学参数表Table 1 Physical parameters of soil

表2 模型参数Table 2 Parameters of different models

表3 不同模型的计算结果Table 3 Results of different models

由表 1、2可知，固结不排水三轴试验得到的内摩擦角和黏聚力与固结快剪的试验结果相比较大，10 m处土体为淤泥质粉质黏土，其应力-应变曲线为典型的应变软化型，具有较强的结构性。由表3可知，应力一次跌落模型的塑性半径最大，四折线模型和三折线模型的相差不大，理想弹塑性模型的最小；理想弹塑性模型的极限扩张压力最大，其次是四折线模型、三折线模型、应力一次跌落模型；四折线模型和理想弹塑性模型的位移计算值与实测值相比较小，且四折线模型的计算值与实测值较接近，三折线模型和应力一次跌落模型的计算值与实测值相比较大，且三折线模型的计算值与实测值较为接近，对比四折线模型和三折线模型可知，四折线模型计算的位移值与实测值更为接近。

6 结 论

（1）提出了四折线应变软化模型各直线段和相应参数的确定方法。

（2）采用Mohr-Coulomb屈服准则和相关联流动法则，得到了桩周不同区域土体的位移、应力和应变，同时得到了极限软化区半径、极限破坏区半径和极限扩张压力的计算公式。

（3）结合工程实例，将四折线应变软化模型与理想弹塑性模型、应力一次跌落应变软化模型和三折线应变软化模型的柱形孔扩张理论进行比较，结果发现，四折线模型和理想弹塑性模型的位移计算值与实测值相比较小，三折线模型与应力一次跌落模型的位移计算值与实测值相比较大，且四折线模型与三折线模型相比，位移值更接近于实测值。

[1]龚晓南, 李向红. 静力压桩挤土效应中的若干力学问题[J]. 工程力学, 2001, 17(4): 7－12.GONG Xiao-nan, LI Xiang-hong. Several mechanical problems in compacting effects of static piling in soft clay ground[J]. Engineering Mechanics, 2001, 17(4): 7－12.

[2]BUTTERFIELD R，BANERJEE P K. Application of electro-osmosis to soils[R]. UK: Department of Civil Engineering, Southampton Univ., 1968, 31(1): 709－715.

[3]VESIC A S. Expansion of cavities in infinite soil mass[J].J. Soil Mech. Found. Div., 1972, 98(SM3): 265－290.

[4]蒋明镜, 沈珠江. 考虑材料应变软化的柱形孔扩张问题[J]. 岩土工程学报, 1995, 17(4): 10－19.JIANG Ming-jing, SHEN Zhu-jiang. Expansion of cylindrical cavity of materials with strain-softening behavior[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(4): 10－19.

[5]姜珂. 考虑软黏土结构性损伤的静压桩沉桩规律分析[D]. 杭州：浙江大学，2003.

[6]方万军. 软土中管桩挤土效应分析及影响研究[D]. 杭州: 浙江大学, 2006.

[7]孙渝刚. 考虑软土结构性损伤的静压桩挤土效应研究[D]. 武汉: 华中科技大学, 2007.

[8]蒋明镜, 沈珠江. 考虑剪胀的线性软化柱形孔扩张问题[J]. 岩石力学与工程学报, 1997, 16(6): 550－557.JIANG Ming-jing, SHEN Zhu-jiang. On expansion of cylindrical cavity with linear softening and shear dilatation behavior[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(6): 550－557.

[9]萧琳琛, 谢新宇, 曹秀娟. 考虑土体结构性损伤的沉桩挤土效应解析分析[J]. 岩土力学, 2006, 27(增刊): 59－64.XIAO Lin-chen, XIE Xin-yu, CAO Xiu-juan. Analytical solutions of squeezing effect caused by pile-driving in soil with structural damage[J]. Rock and Soil Mechanics,2006, 27(Supp.): 59－64.

[10]蒋明镜, 沈珠江. 岩土类软化材料的柱形孔扩张统一解问题[J]. 岩土力学, 1996, 17(1): 1－8.JIANG Ming-jing, SHEN Zhu-jiang. Unified solution to expansion of cylindrical cavity for geomaterials with strain-softening behavior[J]. Rock and Soil Mechanics,1996, 17(1): 1－8.

[11]龚晓南. 土塑性力学[M]. 杭州: 浙江大学出版社, 1990.