重力坝层间抗滑稳定体系的动力可靠度分析方法

张社荣，王 超，孙 博

（天津大学 水利工程仿真与安全国家重点实验室，天津 300072）

1 引 言

由于施工工艺和施工质量的影响，碾压混凝土重力坝具有明显的层状构造，坝体渗漏和层面间抗滑稳定影响坝体安全[1]，特别是动力工况下，受坝基和坝体材料参数不确定性及地震荷载随机性的影响，坝体内部存在潜在滑动失稳层面，坝体体系的层间抗滑稳定安全度[2]必须进行校核。

地震作用下体系抗滑稳定可靠度属于结构体系动力可靠度问题。在此方面，张社荣等[3]采用离散化降维数值解法研究了重力坝水荷载与地震荷载的组合问题，计算了某重力坝的动力抗滑稳定可靠度及相应的地震烈度验算点；胡强等[4]研究了复杂结构体系极限状态方程的拟合和可靠度计算的新方法；陈颖等[5]研究了随机结构在随机荷载作用下的动力可靠度问题；范书立等[6]采用改进拟静力法计算了重力坝动力可靠度，在简化考虑失效路径相关性的条件下研究了重力坝体系的抗震可靠度。徐强等[7－8]研究了动力作用下重力坝受拉失效路径的可靠度及体系可靠度计算方法，并对强度失效路径进行了搜索。

动力可靠度实质上是综合应用动力分析理论和概率理论，在结构随机动力响应分析的基础上对响应结果进行概率统计分析，进而求得结构动力可靠性。重力坝体系层间动力抗滑稳定可靠度分析尚有许多问题需要解决：一方面，地震作用下坝体潜在滑动模式多为人为拟定，滑动失效路径的搜寻没有进行到底；另一方面，坝体层面动力抗滑稳定可靠度估计的方法体系尚需探讨。

本文同时考虑地震荷载和结构参数的双重随机性，通过统计概化，确定结构的潜在滑动失效路径；建立了碾压混凝土坝层面动力抗滑可靠度计算模型。根据体系可靠度理论，考虑不同滑动失效模式间的相关性和地震作用的随机性，采用基于全概率公式的数值拟合积分方法求解层面抗滑稳定体系的动力可靠度。

通过近三天认真细致的审核，专家组认为，泸天化生产设备先进、技术工艺严谨，产品质量可靠，尿素、螯合钾锌等增值尿素生产全过程均对有害物质实施了有效控制，符合HQC《环保生态肥料产品认证实施规则》的要求，并对产品进行了抽样封存，将样品寄到四川省危险化学品质量监督检验所检测。检测结果显示，产品各项重金属及缩二脲指标合格，符合国家环保生态肥料产品的标准和要求，将授予泸天化“国家环保生态肥料产品认证企业”称号。

2 动力抗滑体系可靠度计算方法

2.1 潜在抗滑失效路径的确定

失效模式是指结构失效的方式，它与一定的功能目标相对应。失效路径是指由于结构部分单元在加载过程中会逐步破坏而形成的通道或者薄弱层面。本文研究碾压混凝土重力坝的坝体抗滑稳定失效模式及其对应的失效路径。

目前对失效路径的确定多是基于人为假定。对于常规重力坝，建基面即坝体稳定的薄弱控制面[2]；对碾压混凝土重力坝没有必要对各层面逐一计算，一般仅验算建基面、上下游折坡处层面这些较为确定的路径[6]。但在地震作用下，坝体层面的稳定性受动荷载导致材料性能退化引起的剪应力降低及坝体坝基动力相互作用的影响，坝体抗滑薄弱层面可能会出现各不相同的分布特征，人为拟定不甚科学且容易遗漏一些不易辨识的失效路径。为此，本文以数值试验结果为基础，对潜在的抗滑失效路径进行统计确定。

考虑地震波频谱特性、峰值加速度、坝体、坝基材料参数的随机性，采用统计分析的方法确定动力条件下结构的潜在失效路径，认为结构沿各条路径均可能发生抗滑失稳。具体做法是：选取结构所在场地条件下i组频谱特性不同的地震波，分别按照0.1 g～0.6 g范围内j个不同地震峰值加速度进行调幅，输入k个材料参数不同的结构模型中，采用断裂扩展有限元法（XFEM）研究结构的动力破坏机制，对不同的破坏模式进行统计，并概化为典型的失效路径。经研究表明：该方法统计概化出的失效路径包含了建基面、上下游折坡面这些较为确定的路径，同时也搜索出了其他一些潜在失效路径。基于此进行的概率计算是全面的、保守的。

2.2 功能函数模型的建立

路径 1：基建面上，建基面抗滑失稳（高程为1 192 m层面）；

漏损率是指漏失量和总供水量的比值，其中漏失量为总供水量减去实际使用水量。漏损率高表明水在运输过程中损失多，供水效率低；反之漏水率低说明城镇供水效率高。我国是一个水资源分布不均、人均水资源短缺的发展中国家，降低漏损率很有必要。国家在2016年颁发了《城镇供水管网漏损控制及评定标准》（CJJ92—2016），对今后的城镇供水漏水提出了要求和目标，即在2017年供水管网漏水率达到二级标准12%，2020年达到一级标准10%。而根据《2014年城镇供水年鉴》调查，大部分省份的漏损率都超过了12%，一些省份漏损率甚至高达33%，可见我国的城镇供水效率还有待提高，供水公司压力巨大。

式中：λi、Φi为输入地震动功率谱矩阵的复特征对；g(t)为地震动的调制函数。代入动力反应控制方程：

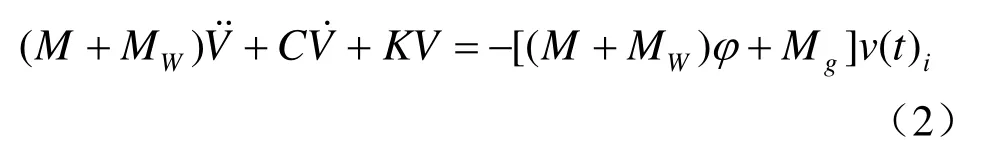
由振型分解法求解，相应的坝体动应力反应为

基层畜牧兽医动物防疫机构是政府设置在基层的负责畜牧兽医防疫工作的机构，对畜牧兽医动物防疫工作的开展具有重要的推动作用。但是，畜牧兽医动物防疫工作并未受到上级政府，尤其是相关主管部门的重视，这主要与相关领导的畜牧兽医防疫观念滞后有关，主要体现在以下几个方面：将畜牧兽医看作“鸡肋”，不重视畜牧兽医防疫工作；管理松散如散沙，监管乏力，缺乏一致性；基层畜牧兽医防疫工作环境恶劣、设备简陋；延迟畜牧兽医防疫工作资金的发放；不注重基层畜牧兽医动物防疫人才的引进培养等。

这里AR、AI均为求解得到的实向量。设 Saa(ω,t)的秩为k′，则动力响应的功率谱密度 Syy(ω,t)为

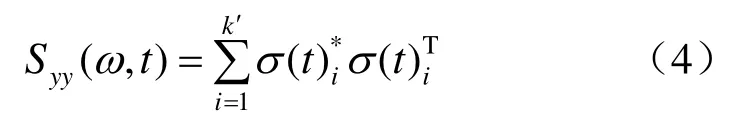
相应的动应力反应的方差为

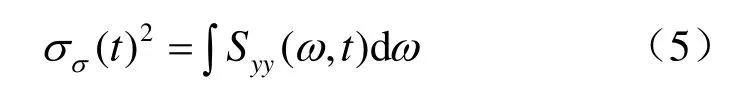
采用工况组合的方法进行静动力叠加，以抗滑稳定作为功能目标，采用刚体极限方程为失效准则建立薄弱层面的极限状态方程式为

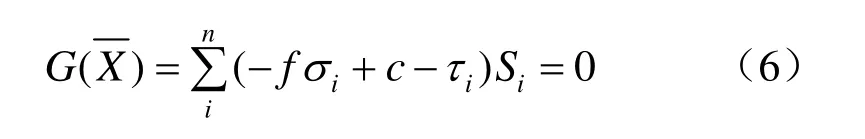
式中：f、c分别为薄弱层面抗剪断摩擦系数及凝聚力；σi、τi为第i个单元的正应力和水平剪应力；Si为第i个单元的面积。

接着进行随机有限元计算，采用响应面函数[9]拟合结构响应与输入荷载及材料参数之间的显式关系，将式（6）表达为

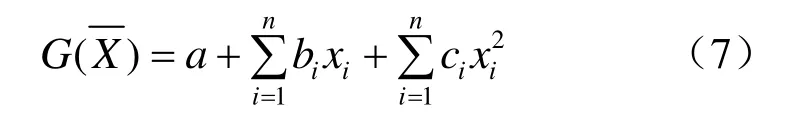
其次，音乐的表现形式具有多样性的特点，既有乐器演奏，也有歌唱配舞，且在音乐创作过程中，需要采风、构思、排练、演出等多个环节，这就为人民群众相互沟通交流提供了诸多平台和渠道。人们通过音乐艺术可以进行情感的交流，在艺术的感染下，潜移默化地消除了很多不必要的矛盾，有利于社会的和谐稳定。

通过上述研究可以看出儿童血脂紊乱的检出率之高。现今人民生活水平的提高,饮食结构的改变,外源性高脂肪,高胆固醇食物的摄入增多,运动减少,肥胖儿童增多等具有一定的相关性,当然,地域差异,家族遗传,被动吸烟,血糖,血压等均对其具有重要的调节作用。因此,为了儿童的健康成长,全社会要高度重视对儿童青少年血脂异常进行防治,首先改变其饮食习惯,增加运动入手。

最后采用基于该响应面方程的 Monte-Carlo法求得相应的可靠度指标β，在此不再赘述。

2.3 考虑失效路径相关性的体系可靠度

碾压混凝土重力坝滑动可靠度是一个串联体系的可靠度问题。本文采用Ditlevsen窄界限区间理论[10]求解层面滑动失效体系的可靠度。

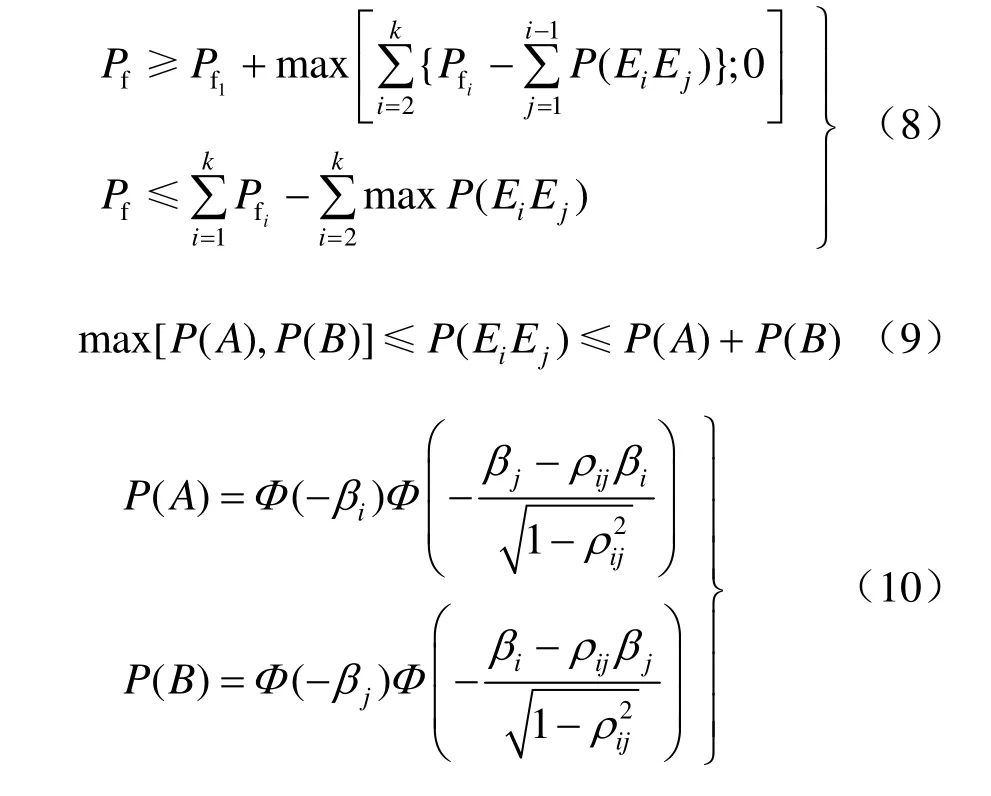
式中：n为随机变量的个数；a、bi、ci为待定参数。这样，结构响应量的统计特性也被计入。

2.4 考虑地震随机性的全概率动力可靠度

例如，对水平地震系数KH=0.3的确定性地震作用下各层面滑动失稳模式进行相关性分析（见表3），采用窄界限公式求得体系失效概率约为0.048 41%～0.048 43%（相应可靠指标约为3.300）。同理，分别计算坝体在不同水平地震系数下的体系抗滑条件失效概率及相应的可靠指标，结果见表 4。由于失效概率较小，本文以对数形式进行描述。对表4的水平地震系数与失效概率上限值的关系进行曲线拟合，得到的拟合函数（如图6）方程为

式中：g为重力加速度。特定地震动峰值加速度作用下的重力坝体系的抗滑稳定可靠度实质上是一个条件可靠度，对应的失效概率为不同水平地震加速度系数条件下的失效概率由于较难用一个精确的解析式进行表达，因此，使用数值拟合积分的方法对上式进行计算[11]。基于全概率公式可以得到体系动力抗滑稳定的失效概率及其可靠指标β：

其实，我父亲还算不得斯文，他才高小呢，当年办学实在缺师资，拿他大队会计赶鸭子上了架。祭祖要讲礼制的，平日里大家再怎么尊重他，学历不够，对不起，祭祖日他就得缩在后面。也只有在“牵猪牯”时，他的身份才突显出来，像个真正的斯文真正的博士。你不妨想象一下，腋下大夹子，手上竹鞭子，迈着方步子，戴着草帽子，率领猪公子，去见猪娘子。那副模样，是不是有点滑稽？其实，父亲还有一样道具，斜挎的军用挎包，里面一管毛笔一瓶墨水，以备不时之需。哦，顺口溜是李打油编的。

式中：f(A)为水平地震加速度系数的概率分布函数；Φ(·)为标准正态分布函数。多失效路径的动力抗滑稳定体系可靠度求解流程如图1所示。

图1 重力坝层间动力抗滑体系可靠度求解流程Fig.1 Flow chart for system reliability of anti-sliding between layers of gravity dam under seismic loading

3 实例分析

对上述150组结果的不同破坏模式进行统计，并概化为6种典型的失效路径，如图3所示。

表1 随机变量统计特征值Table 1 Statistical characteristics of stochastic variables

3.1 滑动失效路径的确定

采用 2.1节所述的统计概化分析方法，选取Koyna波、Chichi波、迁安波等一类场地条件下 5组频谱特性不同的地震波，分别按照 0.1 g～0.6 g范围内6个不同地震峰值加速度进行调幅，输入5个材料参数不同的结构模型中，采用断裂扩展有限元法（XFEM）研究结构的动力破坏机制，共进行了150组计算。断裂扩展有限元框架下的分离裂纹模型可以有效描述混凝土中的裂纹扩展，通过在相关节点的影响域上显式富集非连续位移模式，使得对非连续位移场的表征独立于单元边界，同时保证被富集的位移模式在单元间的协调性，它所使用的网格与结构内部的集合或无力界面无关，从而克服了在诸如裂纹尖端等高应力和变形集中区进行高密度网格剖分所带来的困难，模拟裂纹生成时也无需对网格进行重新剖分。该方法目前已成为模拟裂纹扩展等连续-非连续问题的热点方法之一。采用XFEM研究结构动力破坏机制的相关理论及分析方法参见文献[12－13]，本文不再赘述。在此，仅给出最具代表性的部分随机条件下坝体结构动力破坏的典型断裂扩展模式，如图2所示。（图中括号内为相应的动超载系数）

乘着个性解放的春风她离开了家庭走进了校园，在与传统的家庭伦理抗争一番之后，她选择了逃离这沉重的家庭环境，为了自由。内心的责任感，与生俱来的母性让其回归家庭，而最终却无家可归。这一系列的遭遇让我们看到一位女性在追求其自身解放的过程中的曲折与艰难。女性是脆弱的，一场悲剧往往会触发其内心负罪意识。从曾树生的自我追求路程可以窥见女性解放道路的漫长与曲折。

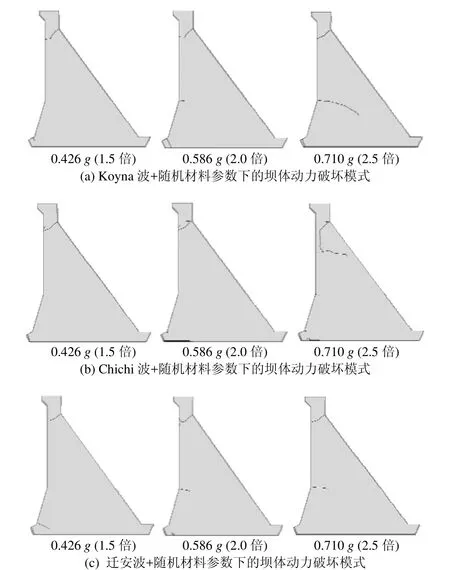
图2 不同随机条件下坝体潜在动力破坏模式Fig.2 Potential dynamic failure paths of dam in different stochastic conditions

某碾压混凝土重力坝，坝高149 m。坝区设防烈度为Ⅷ度，一类场地。100 a超越概率2%的水平向地震动峰值加速度为0.284 g。地震动采取顺河向和竖向两向输入，竖向地震加速度代表值取水平向加速度代表值的 2/3。考虑坝体混凝土材料分区。在动力计算中，坝基取无质量地基，动水压力采用Westergaard公式计算。荷载组合为：上游正常蓄水位水压力+下游相应尾水位水压力+坝体自重+上游淤砂压力+坝基面扬压力+地震荷载。考虑重力坝材料参数的随机性，将变异系数小于0.05的随机变量视为确定性变量，将地震荷载随机变量离散化处理。各参数取值根据地质勘探资料、原设计研究报告及《水利水电工程结构可靠度设计统一标准》（GB50199-94）选取，见表1，限于篇幅，只列出变异系数较大的变量。

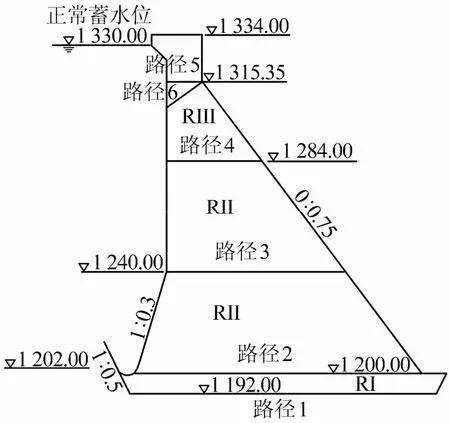
图3 地震作用下坝体典型潜在滑动失效路径 (单位: m)Fig.3 Potential dynamic sliding paths of dam (unit: m)

按规范方法施加静力荷载，动力作用采用虚拟激励法[8]，构造虚拟激励：

重力坝抗滑稳定体系可靠度属于串联体系可靠度问题，首先要对不同滑动失效模式间的相关性进行分析，然后采用Ditlevsen窄界限公式（式8~式10）估算层面滑动体系的失效概率的上下界限。

路径 3：上游折坡处所在层面，失效路径向坝体内部扩展，发生坝体滑动失稳（高程为1 240 m层面）；

路径4：C15与C20碾压混凝土交接层面（高程为1 284 m层面）；

路径 5：坝颈部位，由于分层碾压，可能存在层间薄弱面而形成水平滑动失稳模式（高程为1 315.35 m层面）；

路径 6：下游折坡处附近，由下游折坡点沿45°倾斜向下发展逐渐延伸至上游坡面，失效路径向坝体内部扩展。

我开始忽悠，每个时代都有每个时代的困顿，也许在历史的进程里野蛮会战胜文明，但是要相信，文明的种子在这些市井之辈、读书之人甚至妓女乞丐的心中代代传承，文明不会消亡，总有一天它会变得更有力量。

3.2 不同水平地震系数下层面可靠度

基于响应面法的思想，将不同层面的抗滑稳定极限状态功能函数作为随机输出变量，采用ANSYS PDS模块和APDL语言编制了宏命令，对随机输出变量进行Box-Cox变换，确定合理的变换函数。然后分别拟合了各条滑动失效路径极限状态功能函数的显式表达式，进而求出各个层面的抗滑稳定可靠度见表2。

由图4可知，水平地震系数为0，即静力工况下碾压混凝土重力坝层面的抗滑可靠指标随层面高程的增高而增大，即各层面的抗滑可靠指标的规律都是大致从坝体自顶而下减小，这与文献[1]所得的规律是一致的；但在动力工况下，碾压混凝土坝的层面抗滑可靠指标的规律大致随层面高程的增大而减小，且水平地震系数越大，可靠指标自底向上减小的程度越大。这是由于地震作用下，重力坝动力放大系数随高程增加而增大，坝体自底向上所受的动水平剪应力逐渐增大且在动力抗滑可靠度计算中起控制作用。由图5可知，在地震工况下，不同层面抗滑可靠指标均随水平地震系数的增大而减小。这与实际相符。

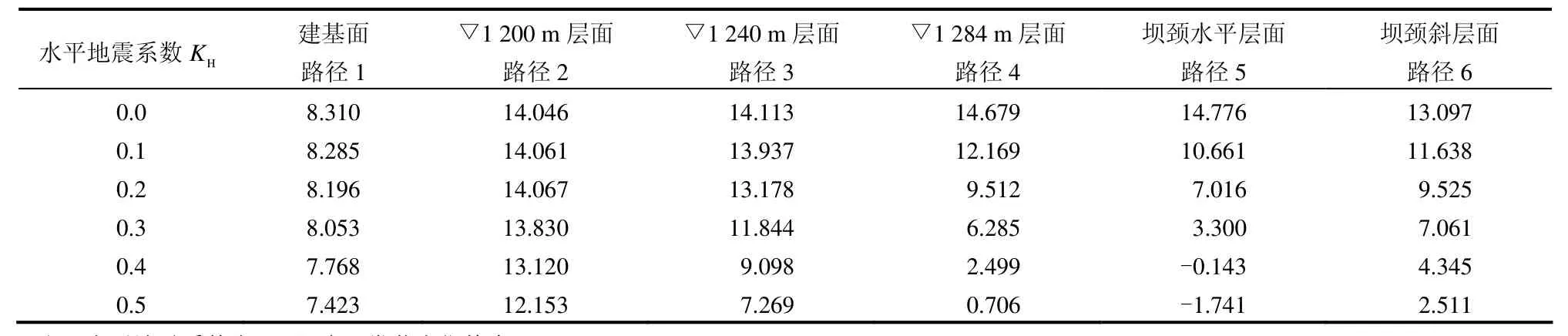
表2 不同水平地震系数下各层面动力抗滑可靠度Table 2 Dynamic sliding reliabilities under different horizontal seismic coefficients

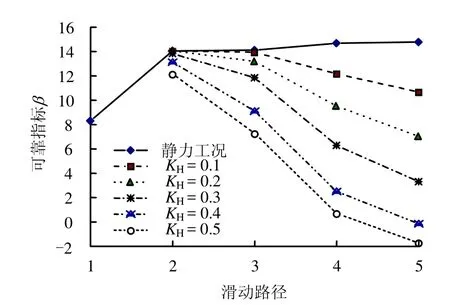
图4 不同高程的路径下层面抗滑可靠度分布Fig.4 Sliding reliability distribution along different elevations

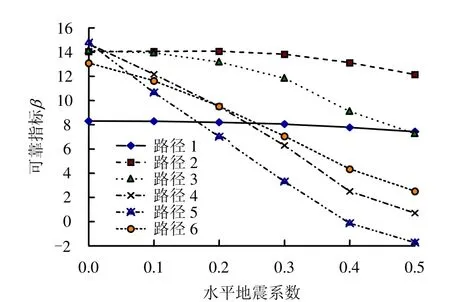
图5 不同水平地震系数下层面抗滑可靠度分布Fig.5 Sliding reliability distributions under different horizontal seismic coefficients

3.3 动力抗滑稳定体系可靠度

路径2：C20与C25碾压混凝土交接层面（高程为1 200 m层面）；

结构抗震可靠度研究中，水平地震系数是一个重要的随机变量。水平向运动峰值加速度A与水平地震系数之间存在关系：

一是积极开拓国内国际市场。充分利用江城县“一城连三国”的地域优势，面向东盟，在勐康国家级口岸和曲水龙富口岸建设国际物流（水果）及交易市场；二是建立果品交易流通平台，积极发展电子商务，为果品批发交易提供服务。

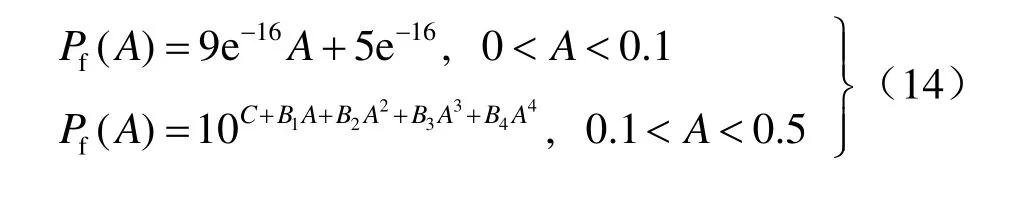
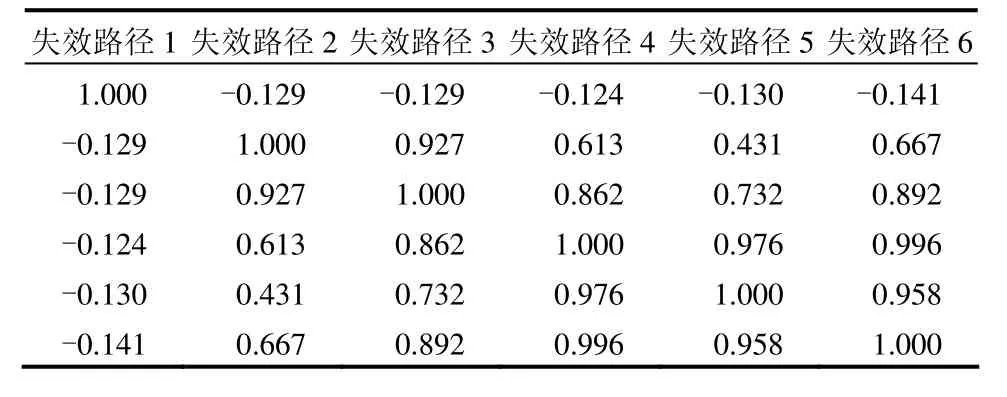
表3 KH=0.3时各典型滑动失效路径相关系数Table 3 Correlation coefficient between correlated sliding failure modes when KH=0.3

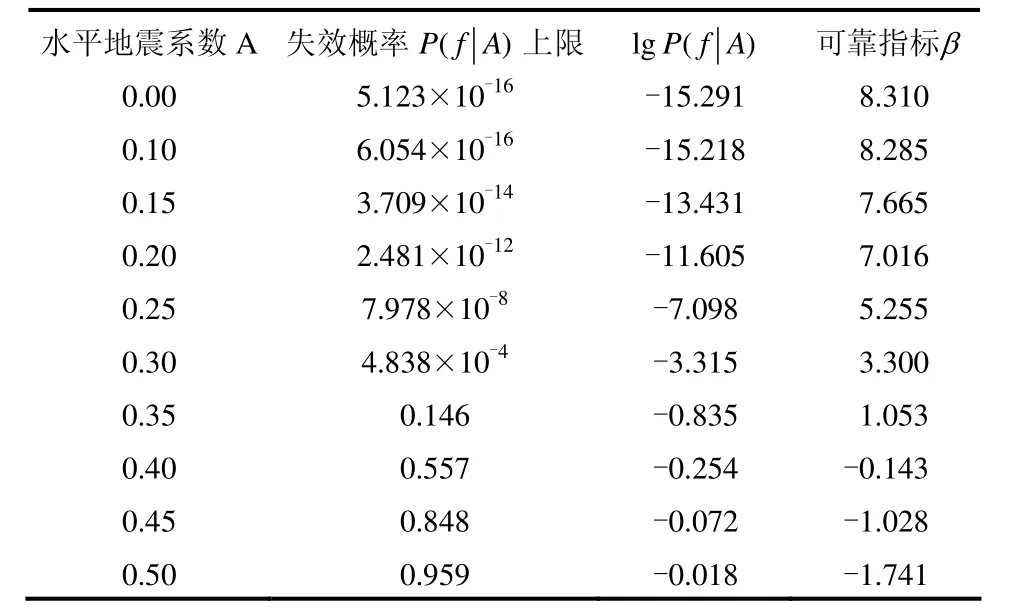
表4 地震作用下坝体抗滑体系可靠度Table 4 Reliabilities of gravity dam system under earthquake

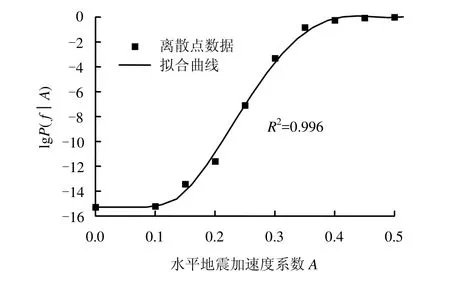
图6 水平地震系数与失效概率（对数值）的拟合关系Fig.6 Fitting curve of horizontal earthquake coefficient and the failure probability（log Kow）

式中：C=-0.997 69，B1=-298.745 10，B2=1 989.311 32，B3=-4 348.655 36，B4=3 144.801 53。该方程在A=0～0.5的区间内拟合优度接近于1。

新时代,我国把“美丽”作为建设现代化强国必须达到的目标。党的十八大把生态文明建设纳入“五位一体”总布局,“美丽中国”成为中华民族追求的新目标;中国共产党更是第一个将生态文明建设写入行动纲领的执政党;十八届五中全会,将绿色发展纳入新发展理念;十九大报告提到“美丽”8次,“生态文明”多达12次,“绿色”15次,首次提出要把我国建成富强民主文明和谐美丽的社会主义现代化强国,强调我们要建设的现代化是美丽的;全国生态环境保护大会上首次提出“构建生态文明体系”,其中就包括“以产业生态化和生态产业化为主体的生态经济体系”;强调“绿色发展是构建高质量现代化经济体系的必然要求,是解决污染问题的根本之策”。

根据文献[14]的研究，水平地震加速度系数的概率密度函数PDF服从下列分布：

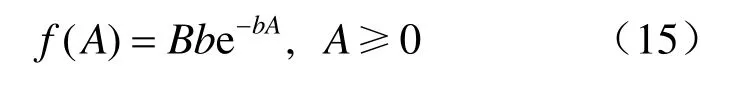
式中：B、b为待定系数，需根据场地的有关地震的统计资料确定。根据现有统计资料，暂取B=0.049 9，b=19.948。

将式（14）和（15）代入式（12）并进行KH=0.5的右截尾计算，得到坝体层间抗滑稳定体系在地震作用下的失效概率为 Pf= 2.881 9 × 10-5，相应的可靠指标为4.022。

穆尔通过动物寓言故事反映人类生活，尽管它们是寓言性的，反映的是现实生活。穆尔在动物世界里找到了自己的生活，展示了一个丰富的自我。从文化批评的角度看，她笔下的动物大多为雌性动物或与女性有关，体现了诗人对女性的关怀。穆尔以严肃的创作态度描写动物、了解动物、尊重动物。她笔下的人与动物是互补的关系。穆尔通过动物诗歌提醒我们，自然界的生灵时刻受到人类的侵扰和控制，人类总是试图成为大自然的主宰。穆尔明确提出，动物有着它们自己的权利，值得被尊重；人类应该学习和模仿自然，而不是控制和征服自然。

对比表2和表4可以发现，KH＜0.2时，坝体抗滑体系的可靠度基本是由建基面抗滑失效路径决定的，而随着地震动峰值的增大，当KH＞0.2时，坝体抗滑体系可靠度不再由建基面失效路径决定，而是由下游折坡处所在层面的失效路径决定，这也体现了地震效应对坝体上部层面的抗滑稳定影响显著。

她坐在他对面，有些摸不着头脑，他为什么要请自己吃晚餐。也许是和她一样找不到一起吃晚餐的人，而又太讨厌一个人坐在喧闹的餐厅里，周围的热闹只会让人的心感觉更孤单。

由此可见，地震效应对坝体层面体系的抗滑稳定影响显著，且在动力工况下，下游折坡点的层面是坝体体系抗滑稳定的控制层面，设计和施工过程中均应引起重视。

4 结 论

本文通过大量数值试验和统计概化的方法研究确定了坝体潜在的滑动失效路径；采用基于全概率公式的数值拟合积分方法求解层面动力条件下的抗滑稳定体系可靠度。可以为相关岩土工程仿真分析中潜在失效模式、失效路径的搜索和动力体系可靠度的求解提供理论借鉴和方法参考。主要结论有：

（1）碾压混凝土重力坝动力条件下抗滑薄弱层面可能会出现各不相同的分布特征，人为拟定不甚科学且容易遗漏一些不易辨识的失效路径。考虑多种因素随机性的统计概化的分析方法，较为全面的搜索出了潜在失效路径。

（2）对多组数值试验的统计表明，地震作用下，挡水坝段坝颈处下游折坡点沿 45°倾角斜向下至上游坡面的倾斜薄弱面是坝体的一条潜在滑动面，不易辨识，抗震设计中需进行稳定验算。

（3）在动力工况下，碾压混凝土坝的层面抗滑可靠指标的规律大致随层面高程的增大而减小，且水平地震系数越大，可靠指标沿高程自底向上减小的程度越大。

（4）随着地震加速度的增大，当KH＞0.2时，坝体抗滑体系可靠度不再由建基面失效路径决定，而是由靠近坝顶的下游折坡处所在层面的失效路径决定，这也体现了地震效应对坝体上部层面的抗滑稳定影响显著。

（5）视水平地震系数为连续型分布，对不同水平地震加速度下的重力坝层面抗滑体系失效概率进行曲线拟合，进而采用数值积分的方法进行抗震可靠度的全概率计算，具有明确的数学意义，计算方法是合理可行的。

[1]朱俊松, 訾进甲, 刘侠, 等. 等壳碾压混凝土重力坝层间抗滑稳定可靠度分析[J]. 中国农村水利水电, 2011,(1): 115－118.ZHU Jun-song, ZI Jin-jia, LIU Xia, et al. A reliability analysis of antiskid stability between the layers of Dengke RCC gravity dam[J]. China Rural Water and Hydropower, 2011, (1): 115－118.

[2]赵会香, 张思俊, 张广键. 龙滩水电站碾压混凝土高重力坝可靠度研究[J]. 水力发电, 1999, (2): 200－203.ZHAO Hui-xiang, ZHANG Si-jun, ZHANG Guang-jian.Study on reliability of high RCC gravity dam of Longtan hydropower station[J]. Water Power, 1999, (2): 200－203.

[3]张社荣, 李振富, 郭怀志. 重力坝抗震可靠度分析[J].天津大学学报, 1991, (增刊2): 137－141.ZHANG She-rong, LI Zhen-fu, GUO Huai-zhi.Earthquake resistant reliability analysis of gravity dam[J].Journal of Tianjin University, 1991, (Supp.2): 137－141.

[4]胡强, 刘宁, 李锦辉. 一种新的可靠度计算方法及其在工程中的应用[J]. 岩土力学, 2004, 25(4): 632－636.HU Qiang, LIU Ning, LI Jin-hui. A new method of structural reliability analysis and its application[J]. Rock and Soil Mechanics, 2004, 25(4): 632－636.

[5]陈颖, 王东升, 朱长春. 随机结构在随机载荷下的动力可靠度分析[J]. 工程力学, 2006, 23(10): 82－85.CHEN Ying, WANG Dong-sheng, ZHU Chang-chun.Dynamic reliability analysis of stochastic structures subjected to random loads[J]. Engineering Mechanics,2006, 23(10): 82－85.

[6]范书立, 陈健云, 范武强, 等. 地震作用下碾压混凝土重力坝的可靠度分析[J]. 岩石力学与工程学报, 2008,27(3): 564－571.FAN Shu-li, CHEN Jian-yun, FAN Wu-qiang, et al.Reliability analysis of roller compacted concrete gravity dams subjected to earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 3(3): 564－571.

[7]徐强, 陈建云, 李静, 等. 非平稳地震动过程中混凝土重力坝受拉失效路径可靠度分析[J]. 工程力学, 2011,28(3): 123－128.XU Qiang, CHEN Jian-yun, LI Jing, et al. Concrete gravity dam reliability analysis on tension failure path under non-stationary ground motion processes[J].Engineering Mechanics, 2011, 28(3): 123－128.

[8]徐强, 陈建云, 李静, 等. 基于贝叶斯理论的大坝体系可靠度计算方法[J]. 大连理工大学学报, 2011, (1): 84－89.XU Qiang, CHEN Jian-yun, LI Jing, et al. Calculation method for system reliability of dam based on Bayes theory[J]. Journal of Dalian University of Technology,2011, (1): 84－89.

[9]颜立新, 康红普, 高谦. 基于响应面函数的可靠度分析及其应用[J]. 岩土力学, 2001, 22(3): 327－333.YAN Li-xin, KANG Hong-pu, GAO Qian. Reliability analysis based on response surface function and its application to a chamber[J]. Rock and Soil Mechanics,2001, 22(3): 327－333.

[10]DITLEVSEN O. Narrow reliability bounds for structural system[J]. Structural Mechanics, 1979, 7(4): 453－472.

[11]贾超, 刘宁, 陈进. 地震作用下土坡可靠度风险分析[J].岩石力学与工程学报, 2005, (04): 703－707.JIA Chao, LIU Ning, CHEN Jin. Slope risk analysis under the earthquake effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, (04): 703－707.

[12]ABDELAZIZ Y, BENDAHANE K, BARAKA A.Extended finite element modeling[J]. Basic Review and Programming Engineering, 2011, 3: 713－718.

[13]方修君, 金峰, 王进廷. 基于扩展有限元法的Koyna重力坝地震开裂过程模拟[J]. 清华大学学报(自然科学版), 2008, 48(12): 2065－2069.FANG Xiu-jun, JIN Feng, WANG Jin-ting. Seismic fracture simulation of the Koyna gravity dam using an extended finite element method[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(12):2065－2069.

[14]MECANN W. Seismic hazard map for Puerto Rico 1994[R]. Puerto Rico: Seismic Safety Commission Puerto Rico, 1994.