水井反冲洗地层三维弹塑性固结分析

王素玲，李 杨，沈新普，刘勤志

（1. 东北石油大学 机械科学与工程学院 黑龙江 大庆 163318 ；2. Halliburton Energy Service Citywest Blvd., Bldg2 Houston, TX 77042, U.S.；3. 中国石油天然气股份有限公司，北京，100007）

1 引 言

目前，水压驱油仍然是提高采收率最有效的方式之一，但由于受注入水质和注入工艺的影响，导致井壁污染后致使注入受阻而引起产量下降。洗井是抽油机井维持正常生产的重要工艺之一[1]。

在实际工程中，影响洗井工艺和洗井效果的因素较多。目前，人们主要关注的是洗井压力对套管挤压破坏产生的影响[2－3]，而忽略了地层在反冲洗过程中对套管的作用。在注水井反冲洗过程(泄压)中，由于套管内流体压力骤降，导致在注水井井底与地层之间存在较大的流动压差，从而孔隙压力的变化导致地层有效应力发生变化。在地应力作用下，套管所承受的径向挤压力增大，地层遭到挤压破损，将导致套管损坏。为了避免引发套管损坏造成反冲洗事故，对套管承载能力进行分析具有重要的理论意义及工程应用价值。

本文使用 ABAQUS-6.5软件，在考虑流固-耦合条件下，以套管和油藏岩体为研究对象，建立了油藏岩石的反洗井围岩和套管的三维固结分析模型，分析反洗井的渗流过程及套管变形过程。结合反冲洗井工艺和岩石变形固结的过程被视为流体-固体多场耦合的弹塑性问题，计算中采用Mohr-Coulomb条件作为岩石的屈服条件。研究了不同岩体性质及反冲洗工艺对套管承载能力的影响，为反冲洗作业中压力控制提供理论依据，减小施工的盲目性，在最大提高冲洗效果的同时，保护套管不受损坏。

2 注水井反冲洗力学模型

为了能够较详细地模拟围绕射孔周边岩石的力学行为，考虑到射孔尺寸很小，取射孔段套管和地层为研究对象，取岩层厚度为1 m、半径为2 m的三维部分岩石分析固结情况。

井筒内以螺旋形式分布射孔眼，套管内径为φ124.26 mm，外径为φ139.7 mm，管内充满洗井液(清水)，力学模型如图1所示。

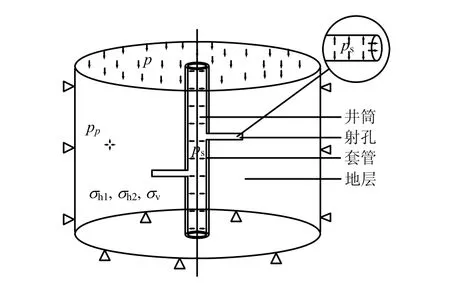
图1 套管-地层力学模型Fig.1 Mechanical model of casing-formation

边界条件为：①下表面施加z方向的位移约束，模拟下部地层对模型的支撑作用；②在外表面施加水平方向的位移约束，模拟外围地层对模型的约束作用；③上表面施加上覆岩石压力，模拟上覆岩层对模型的挤压作用；④施加初始地应力场：σh1、σh2、σv；⑤施加岩层重力，以平衡地应力；⑥施加初始孔隙压力场和初始孔隙率场；⑦在井筒上和射孔壁上施加流体压力，模拟注水压力对套管和地层的作用；⑧在射孔壁上施加大小与流体压力相等的孔隙压力，模拟注水过程中洗井液向地层内渗流对套管应力的影响；采用了载荷函数施加注水压力和射孔壁上的孔隙压力，以模拟流体压力随时间的变化过程。

根据力学模型建立几何模型，并采用13 177个节点，5 584个单元离散几何模型，套管采用 638个非协调实体单元C3D8I离散，在非射孔区域和离套管比较远的区域，划分比较粗的网格就可以满足计算精度，以减少计算时间；在射孔眼附近存在应力集中现象，需要划分较细的网格来提高计算精度。有限元模型和局部放大图如图2所示。

图2 套管-地层整体网格模型和局部放大图Fig.2 Finite element model near well region

3 地层三维固结模型

根据孔隙介质微元体的力平衡方程，采用虚功原理，建立岩体应力平衡方程为

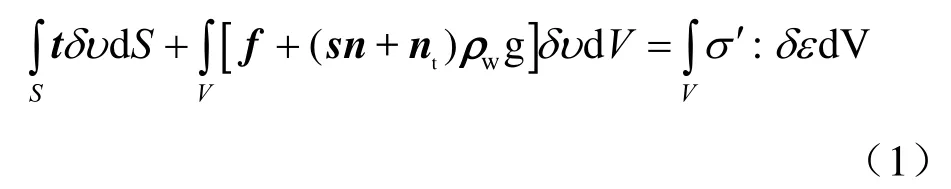
式中：t为微元体表面的cauchy应力；υ为虚速度；S为微元体表面积；f为岩体骨架的体积力；s为饱和度；n为孔隙率；nt为岩体吸附的液体体积；ρw为当前构型下液体密度；σ′为有效应力；ε为微元体应变；V为微元体的体积。

根据微元体内流体质量守恒方程非线性渗流定律，可得到低渗透储层渗流流体平衡方程为

式中：uw为虚孔隙压力；为初始构型下液体密度；J为雅克比矩阵；k为渗透率；β为速度系数；为渗流速度。

根据有限元理论对上述方程进行离散，得到其有限元格式。

应力平衡方程为

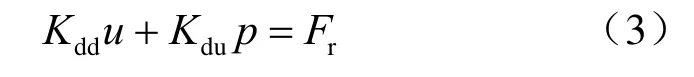
孔隙流体连续性方程为

其中

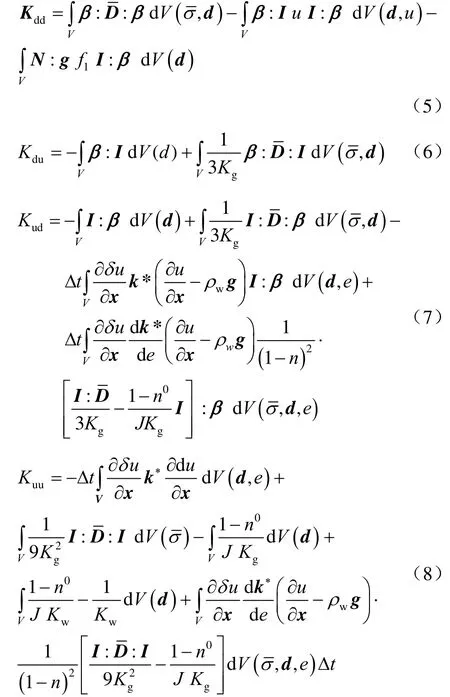
式中：β为应变-位移矩阵；D为本构矩阵；N为插值函数；Kg和Kw是固体颗粒和流体的体积模量;k*是渗透系数向量。

4 数值计算

以某油田的注水井为例，地层弹性模量为12 GPa，泊松比为0.22，初始孔隙度为0.2；套管材料的弹性模量206 GPa，泊松比0.3，屈服强度551 MPa，套管材料的应力-应变关系如表1。2个方向的水平地应力为， σh1=σh2=30 MPa ，垂直地应力σv=24 MPa，洗井深度为1 000 m，注水压力20 MPa（井口压力），洗井液的压力梯度为10 kN/m，初始孔隙压力为10 MPa，卸载压差为20 MPa。

表1 N80套管材料应力-应变关系Table 1 Relationship between stress and strain of material of casing N80

计算过程主要包括：①施加初始地应力、上覆压力、地层重力及边界条件、模拟初始地应力场；②施加注水压力和孔隙边界，模拟注水过程；③卸载注水压力，模拟泄压过程。

图3 平衡地应力场后的垂向变形云图Fig.3 Vertical deformation nephogram after balance of initial geostress field

由图3可以看出，地层垂直方向位移的最大值为0.088 mm，说明地应力与重力场平衡较好，采用上述模型可以反映赋存岩体的应力、应变分布状态。

图4 不同时刻泄压瞬时套管应力变化Fig.4 Changes of casing stress in different pressure release times

泄压瞬间套管Mises应力剧烈上升，主要是因为在注水井泄压之前，注水井套管内壁作用有很高的注水压力，它作为支护力使套管较稳定。突然泄压时由于套管内液体压力突然降低，套管失去了支护力，导致套管承受的外挤压力升高，套管应力也瞬间增大。根据应力云图的分布可以看出，射孔眼位置处的应力值较大，这是由于应力集中引起的。因此，套管在水压力的作用下，首先在射孔眼位置处发生破坏，以射孔眼为中心，破坏依次向外传递。

图5 射孔眼附近一点岩石有效应力和孔隙压力随时间变化曲线Fig.5 Effective stress and pore pressure in rocks around the perforation eye varies with time

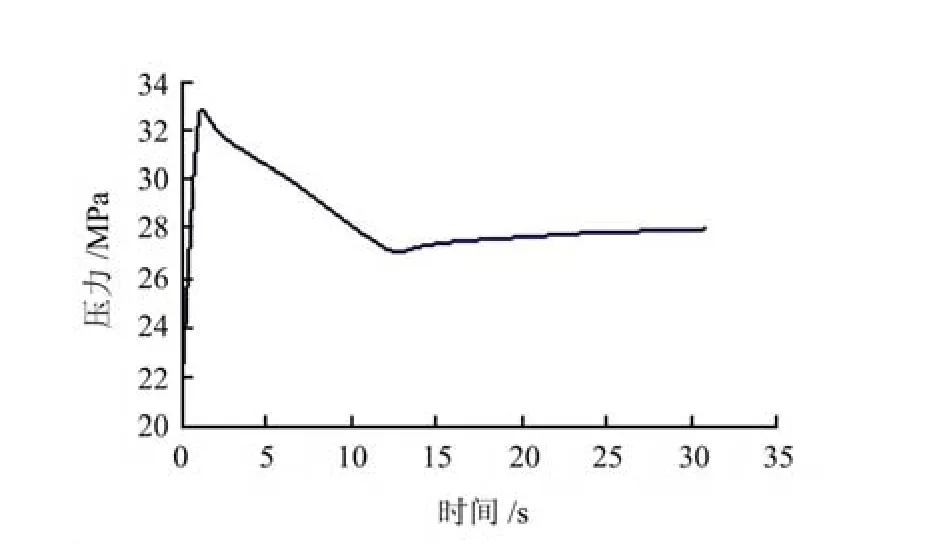
图6 套管挤压力随时间变化曲线Fig.6 Casing external pressure curve varies with time

由图5、6可以看出，泄压时射孔眼附近流体压力下降最快，致使岩石骨架承受的有效应力急剧上升；同时，射孔表面的流体压力和孔隙压力突然降低，远处的孔隙压力大于射孔眼附近的孔隙压力，流体由地层向井筒内渗流，多方面因素的共同作用，导致套管损坏。

套管所受的挤压力和套管应力在泄压瞬间上升最快，变化最剧烈，随着时间的推移，挤压力和套管应力都将趋于平稳。由此可知，泄压瞬间套管最易损坏。

5 水井反冲洗压力的影响因素分析

地层的岩性及地应力分布状态影响反冲洗过程中载荷的变化，为了考察上述因素，在计算中分别改变了岩石的渗透率、弹性模量和地应力状态。

5.1 地层渗透率对洗井压力的影响

地层按渗透率分类，可以分为高、中、低以及特低渗透率地层。对于不同的地层，应力敏感性表现差异较大，变化规律各不相同。计算中，根据文献[4－5]中推荐的不同地层条件下，孔隙度与渗透率的变化规律。图7为不同渗透率下泄压瞬时地层中孔隙压力的分布状况。

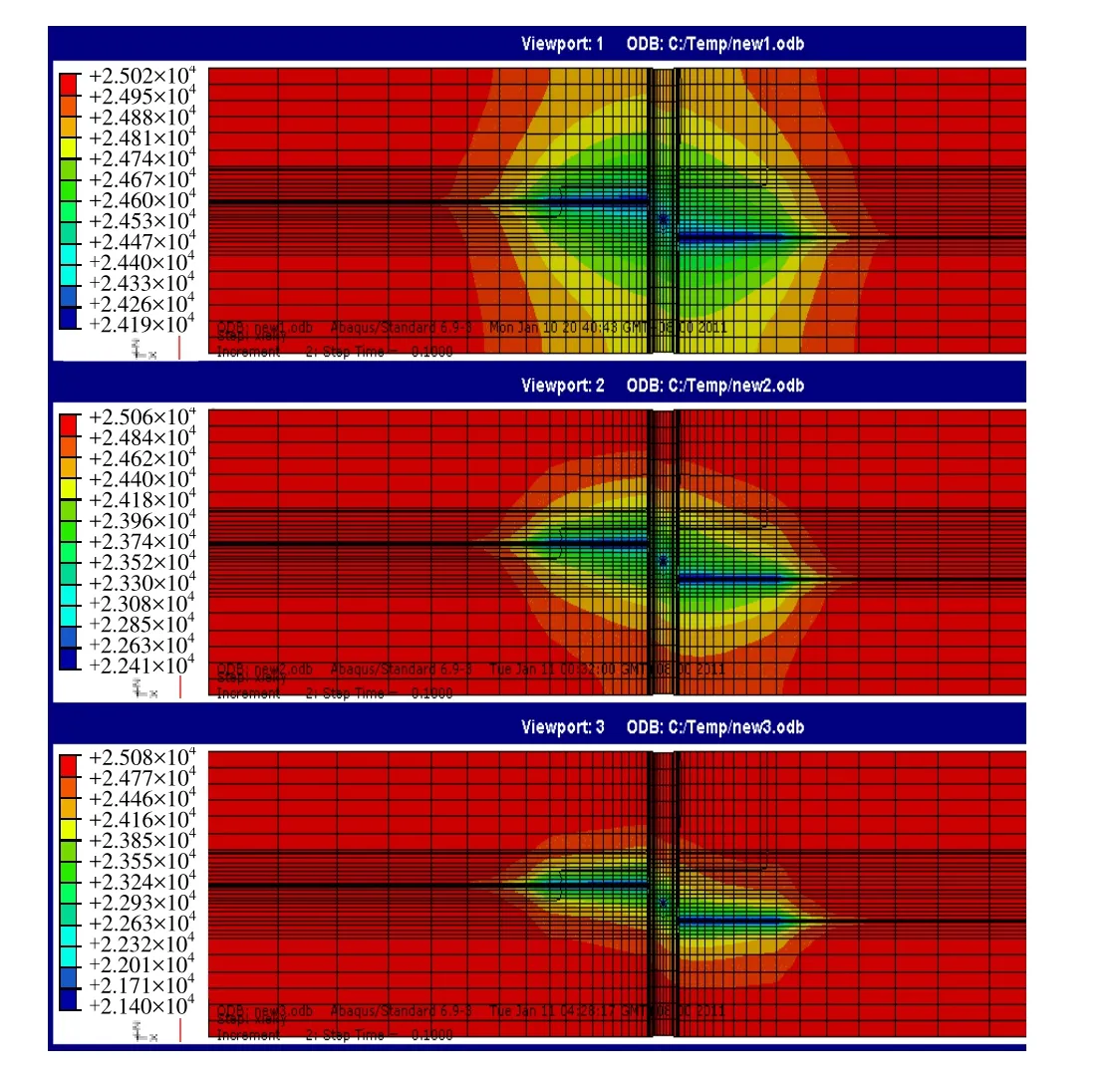
图7 泄压瞬间不同渗透率地层孔压分布对比Fig.7 Pore pressure distributions when pressure release in different permeabilities

图8 安全洗井压力与地层渗透率关系Fig.8 Relationship between safe backwash pressure and permeability

从图7可以看出，在其他条件相同时，渗透率越低，泄压瞬间地层中液体反向渗流量越小，井眼周围地层中的孔隙压力越接近正常的注水压力，地层给套管的挤压力越大，井眼内外压差越大、越容易引起井眼周围的应力集中，使注水井套管发生变形。图8为不同地层渗透率下套管所能够承受的安全洗井压力。

渗透率越低，洗井过程中井筒内外压差变化较小，地层有效应力变化较低，套管受挤压力变形小。

5.2 地层弹性模量对洗井压力的影响

计算时，地层的弹性模量分别取7、12、17 GPa，计算各自对应的套管承载能力。图9为不同弹性模量地层变形下地层的变形云图。

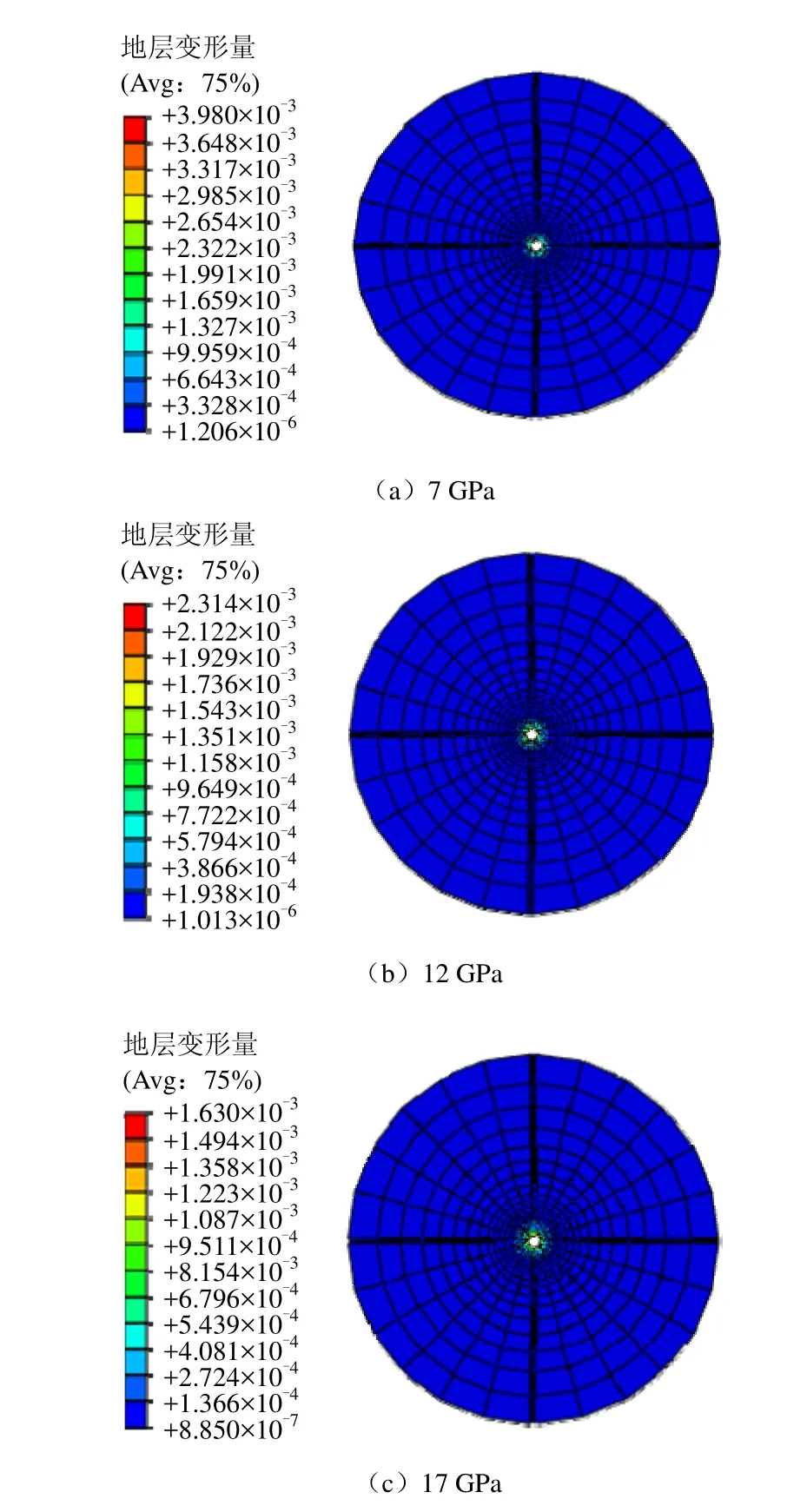
图9 不同弹性模量地层变形量对比Fig.9 Comparison between deformations of strata with different elastic moduli

图10 不同弹性模量地层下洗井压力对比Fig.10 Comparison between backwash pressures of strata with different elastic moduli

由图9、10可以看出，地层的弹性模量越大，套管能承受的最大洗井压力越大。这是因为：地层的弹性模量越大，相同条件下地层的变形越小，地层施加在套管的挤应力越小。如图9所示，在相同条件下弹性模量为7 GPa的地层变形量最大，其值为3.98 mm，弹性模量为12 GPa的地层变形量为2.31 mm，弹性模量为17 GPa的地层变形量最小，其值为1.63 mm。

5.3 地应力分布对洗井压力的影响

由于地应力分布的不均匀性，不同区块地应力的差别比较大，套管损毁的情况也不尽相同，计算中，分别改变垂向地应力及水平地应力，计算结果见表2。

表2 不同垂直应力套管承受的洗井压力Table 2 Backwash pressures of casing in differnent vertical stresses

由表可以看出，垂直地应力对套管承载能力的影响非常小，这是因为地层的垂直地应力是由上覆岩层的重量引起的，只要不发生地壳运动，垂直地应力和上覆压力基本处于平衡状态，相互抵消，作用在套管上的应力很小。

水平地应力不均度是指最小水平地应力与最大水平地应力的比值。实际中，最小水平地应力和最大水平地应力的值一般相差较大，显示出很强的方向性。 σhminσhmax一般为0.2～0.8，在多数情况下为0.4～0.8，参见文献[6]。计算中，假设最大水平地应力为定值30 MPa，分别计算应力不均度为0.5、0.6、0.7、0.8、0.9时套管的承载能力，研究水平地应力不均度（载荷不均度）对套管承载能力的影响，计算结果如表3所示。

表3 不同水平地应力套管承受的最大洗井压力Table 3 Backwash pressures of casing in differnent horizontal stresses

由表3可知，套管的承载能力随水平地应力不均度的减小逐渐增大，承受非均匀载荷时套管的承载能力低于承受均匀载荷时的承载能力，载荷不均匀度对套管的承载能力有很大的影响，随着2个水平主应力的差值变大，套管承载能力减小。

6 结 论

（1）地层的渗透率对洗井压力影响较大，渗透率越低，地层泄压速度越慢，导致套管的内外压差越大，套管越易损坏，则洗井的安全压力越低。

（2）地层的弹性模量越大，在相同的洗井压力下，地层的变形量越小，对套管的挤压力越小，套管不易损坏，则洗井的安全压力越大。

（3）地层的垂直地应力对套管损坏影响较小，水平地应力均匀时套管的承载能力较强，地层水平地应力的不均匀程度越高，套管的承载能力越低，允许的洗井压力越小。

[1]鲁青玲, 高瑞, 董睿, 等. 洗井对油井含水的影响因素分析[J]. 石油地质与工程, 2009, 23(6): 108－110.LU Qing-ling, GAO Duan, DONG Rui, et al. The influencing factor on the oil well water when wash well[J]. Petroleum Geology and Engineering, 2009,23(6): 108－110.

[2]尹中民, 武强, 刘建军, 等. 注水井泄压对套管挤压力影响的数值模拟[J]. 岩石力学与工程学报, 2004,23(14): 2390－2395.YIN Zhong-min, WU Qiang, LIU Jian-jun, et al.Numerical simulation on effect of pressure relief of water injection well on casing squeeze pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2004,23(14): 2390－2395.

[3]杨斌, 练章华, 刘景超. 射孔套管剩余强度有限元分析[J]. 西部探矿工程, 2006, 8: 193－195.YANG Bin, LIAN Zhang-Hua, LIU Jing-chao. Perforated casing residual strength finite element analysis[J]. West China Exploration Engineering, 2006, 8: 193－195.

[4]秦空, 秦岭, 葛秋现. 砂岩中渗透率—孔隙度相关趋势的演化[J]. 国外测井技术, 2001, 16(4): 35－40.QING Kong, QING Ling, GE Qiu-xian. Sandstone in permeability-porosity related to the evolution of the trend[J]. Foreign Well Logging Technology, 2001, 16(4):35－40.

[5]孙玉学, 孔翠龙, 王瑛琪. 低渗透砂岩储层应力敏感性研究[J]. 科学技术与工程, 2009, 9(15): 4448－4450.SUN Yu-xue, KONG Cui-long, WANG Ying-qi. Stress sensitivity of low-permeability sandstone reservoir[J].Science Technology and Engineering, 2009, 9(15): 4448－4450.

[6]于学馥, 郑颖人. 地下工程围岩稳定分析[M]. 北京:煤炭工业出版社, 1983: 67－82.