水平条分法下边坡稳定性分析与计算方法研究

邓东平，李 亮

（中南大学 土木工程学院，长沙 410075）

1 引 言

在边坡稳定性分析方法中，极限平衡法作为一种非常有效的分析方法被广泛应用[1]。目前，极限平衡法多为竖直条分法[2－10]，且在安全系数求解时对条间力所建立的假设条件也是针对竖直条分法[11－14]。然而，竖直条分法尽管有其优势，但当边坡成层岩土体时，竖向条分体内部受岩土体性质变化影响较大，这样会给计算带来极大的不便[15]，因此，这时水平条分法更具有适用性。

文献[16]在一般条分时通过借用竖直条分法的条间力假设条件进行了安全系数的推导，发现当条分不再为竖直条分时，计算得的安全系数与竖直条分法相差较大。同时，在针对水平条分法研究中，国内外大多数文献关注于有加固措施的边坡稳定性，如加筋土[17－19]、锚杆（索）[20]等。文献[1, 15]指出，这些研究没有针对普通边坡的稳定性分析，而且要么有些计算假定过于复杂，不利于工程应用，要么有些过于简单，使计算结果误差较大。另外，目前针对一般边坡稳定性的水平条分法，所涉及到的算例分析一般是认为滑动面比较适合水平条分划分，而对于一般型式下的滑动面，如存在一段弓形体时，水平条分则表现出条分界限不明，弓形体以下水平条分出现两个滑动底面的缺点。

综上所述可知，在边坡稳定性水平条分法极限平衡分析中，存在如下不足：①过少对水平条分的条间力进行分析；②没有将竖直条分法与水平条分法的条间力假设条件相对应；③没有在滑动面为一般型式的条件下，对水平条分法如何进行稳定性分析采取相应处理方法。

本文通过对水平条分和竖直条分中条间力的关系进行分析，建立起水平条分法与竖直条分法相对应的条间力假设条件，并对滑动面存在弓形体的一般情况，将水平条分法采用斜条分与水平条分相结合的模式进行处理。在此基础上，推导出了一些方法在水平条分时的安全系数计算公式。当使用圆弧滑动面和任意曲线滑动面两种型式时，通过算例分析，并与竖直条分法和以往研究成果相对比，验证了本文针对水平条分研究的可行性。

2 水平条分存在的问题及处理方法

在水平条分法中，以往研究成果对如下问题研究不足：①条间力的分析，如图 1(a)所示；②滑动面型式没有针对更为普遍的情况，如图1(b)、(c)、(d)所示滑动面存在一段弓形体。

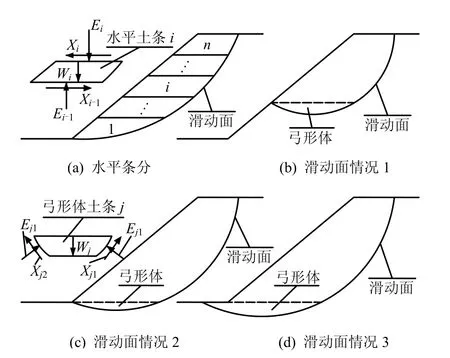
图1 水平条分条间力和存在弓形体的滑动面Fig.1 Inter-slice forces of horizontal slice and sliding surface with presence of toxoplasma

2.1 水平条分条间力分析

当水平条分法直接使用竖直条分法对条间力的假定时需研究其可行性。如图2所示，abcd为水平土条为竖直土条分别为水平土条 i上下底面的条间法向力和剪切力，分别为竖直土条i左右侧面的条间法向力和剪切力，分别为水平土条i和竖直土条 i共有滑动底面的法向力和剪切力，分别为水平土条i和竖直土条i的重力。

图2 水平条分条间力与竖直条分条间力关系Fig.2 Relation of inter-slice forces between horizontal slice and vertical slice

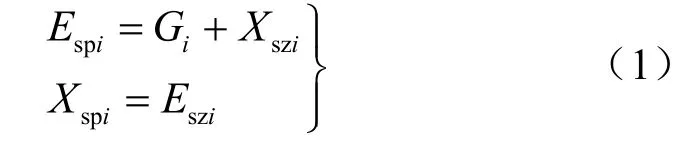
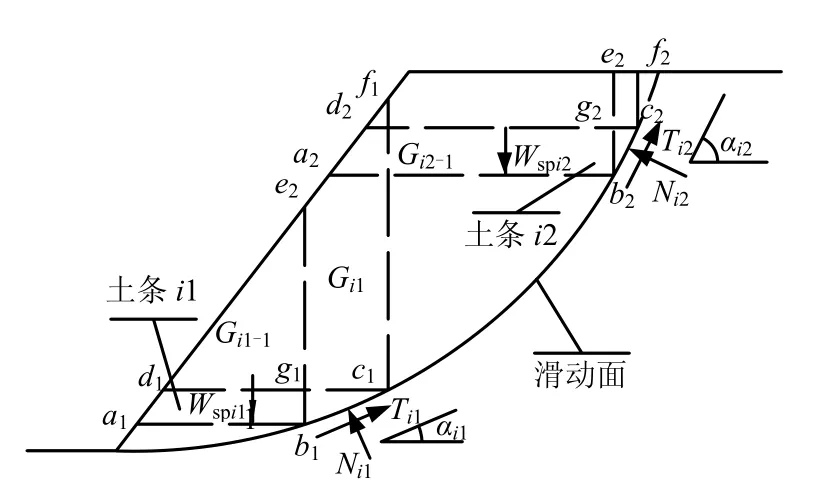
图3 水平条分条间力假设条件分析Fig.3 Assumption analysis of inter-slice forces of horizontal slice

（2）对于简化Bishop法和简化Janbu法，竖直条分：

（3）对于M-P法，

2.2 一般滑动面情况下的处理方法

从图1（b）、（c）、（d）中的3种滑动面情况可知：当滑动面存在一段弓形体时，若使用水平条分，则会出现两个滑动底面，因而对该处土条的受力求解带来麻烦，并造成水平条分界限不清的缺点。为此，本文采用如图4（a）所示的条分法，在下滑点A及其水平延长线以下的弓形体采用水平间距为且过A点的斜条分（条分数为n2），下滑点A及其水平延长线以上仍然采用水平条分（条分数为n1）。

图4 一般滑动面情况下水平条分法的处理Fig.4 Treatment of horizontal slice method undergeneral situation of sliding surface

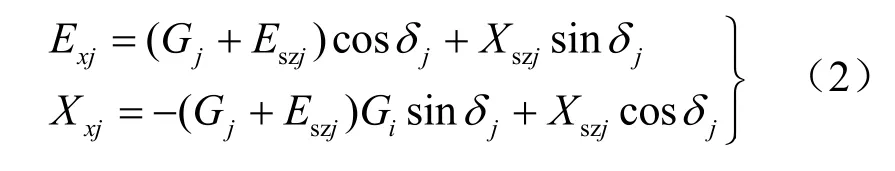
按照2.1节所述，在斜条分中，为了建立起与竖直条分相等效的合理条间力假设条件，本文以式（2）为基础，得到了如下相应计算方法的斜条条间力假设条件。

（1）对于瑞典法：

（2）对于简化Bishop法和简化Janbu法：

（3）对于M-P法：

3 安全系数计算方法

如图5所示，水平条分的土条i上各力对滑动底面法向、切向的力平衡和对滑动底面中心点的力矩平衡如式（3），斜条分的土条j上各力对滑动底面法向、切向的力平衡和对滑动底面中心点的力矩平衡如式（4）。

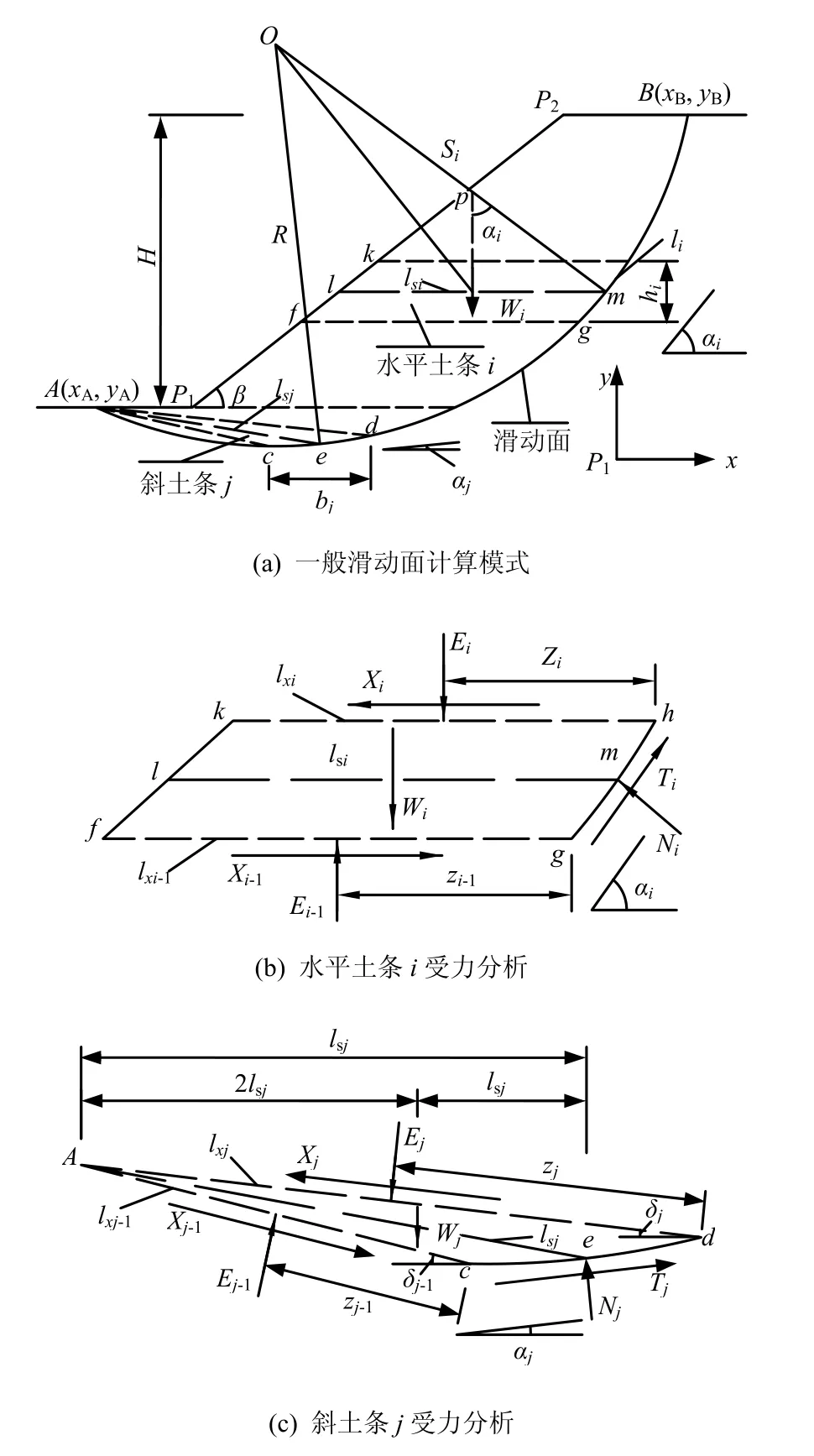
图5 水平条分和斜条分受力分析Fig.5 Stress analysis of horizontal slice and oblique slice

（1）瑞典法

由单个土条体的x轴和y轴平衡，以及滑动土体对滑动圆弧圆心的力矩和满足或土条底面下滑力和抗滑力的总和满足分别得到安全系数的计算式（5）、（6）。

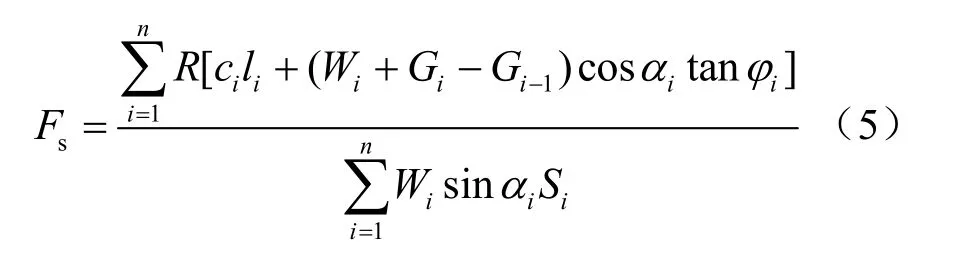
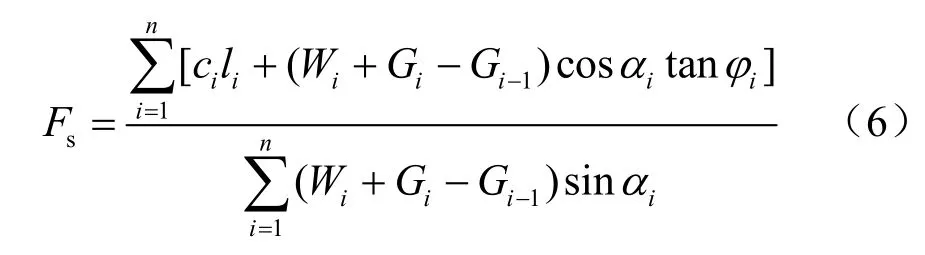
（2）简化Bishop法

由单个土条体的y轴平衡，以及滑动土体对滑动圆弧圆心的力矩和满足得到安全系数的计算公式如式（7）。

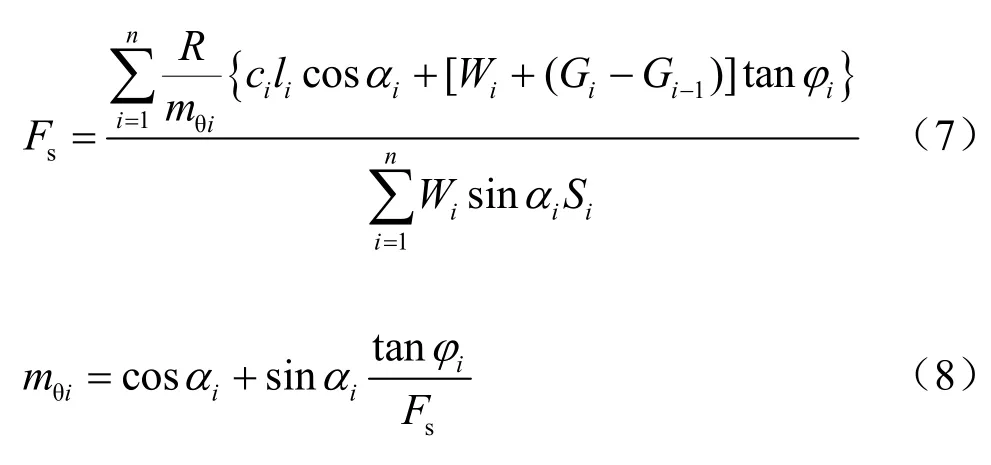
（3）简化Janbu法

由单个土条体的x轴和y轴平衡，得到安全系数的计算公式如式（9）。

同时，有些文献[21－22]对竖直条分法中简化Janbu法进行了改进，即将式（9）分子中的直接乘入到分母，本文也对式（9）进行同样改进，得到安全系数的计算公式如式（10）。

（4）M-P法

由单个土条体的滑动底面法向和切向力平衡，以及对土条滑动底面中心点的力矩平衡，得到安全系数的计算公式如式（11），及式中水平条分和斜条分时的各参数量的计算如式（12）～（21）。

水平条分时：

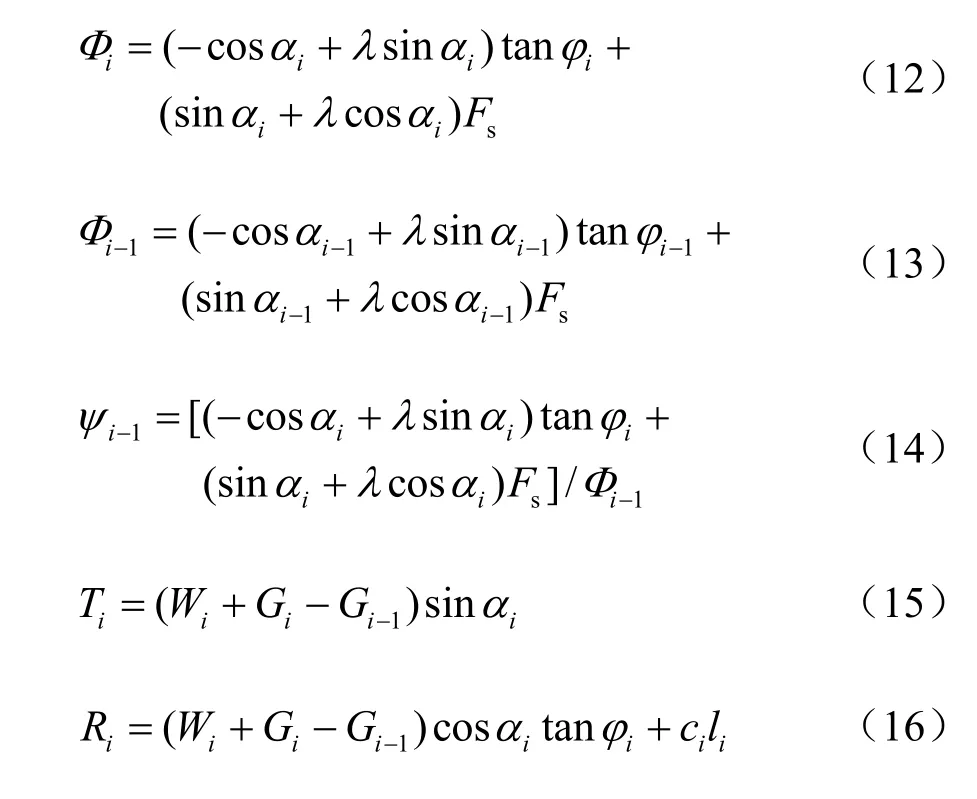
斜条分时：

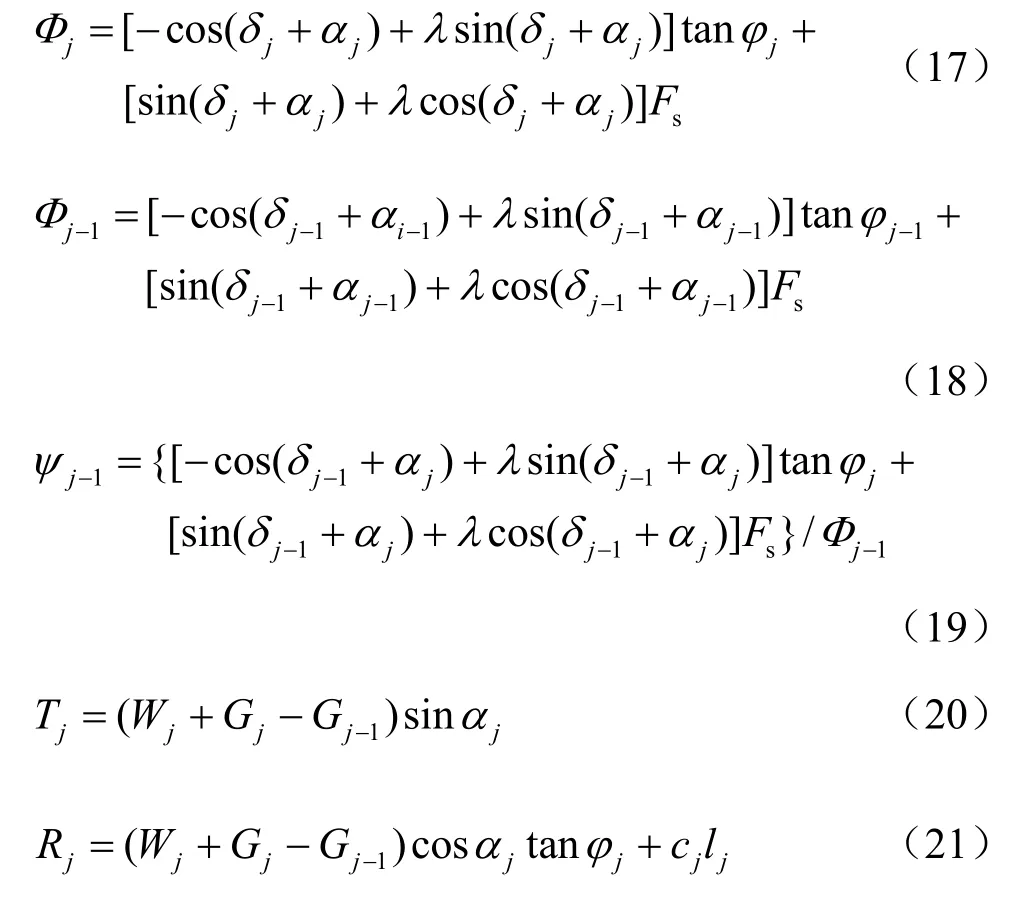
水平条分时

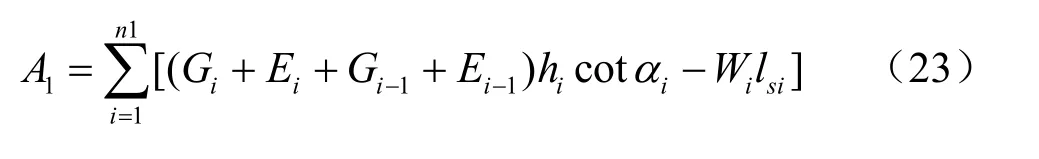
斜条分时

4 计算对比分析

4.1 均质边坡

[23]，选择 3个算例进行对比分析，如图6～8所示。其中，对于任意曲线滑动面，采取文献[21]方法。算例参见表1。

算例1～3计算得的最小安全系数见表2，得到的临界滑动面如图6～8所示。

从表2可知：本文各方法在水平条分时，计算得的安全系数与竖直条分法和文献[23]方法较接近，说明本文对水平条分不足所采取的处理方法可行；水平条分法时，两种瑞典法计算的安全系数基本一致；水平和竖直条分法下的一般简化Janbu法（即简化Janbu法式（9））计算得的安全系数偏小，改进的简化Janbu法（即简化Janbu法式（10））计算得的安全系数与简化Bishop法和M-P法颇为接近，说明改进简化Janbu法对边坡的稳定性评判更准确些。

从图6～8可知：水平条分法和竖直条分法下，本文各方法得到的临界任意曲线滑动面和临界圆弧滑动面与文献[23]得到的临界滑动面较接近；临界任意曲线滑动面近似于圆弧滑动面，但表现为非圆弧型；水平条分下的两种瑞典法得到的临界圆弧滑动面基本相同；一般简化Janbu法得到的临界滑动面的范围较其他方法要大。

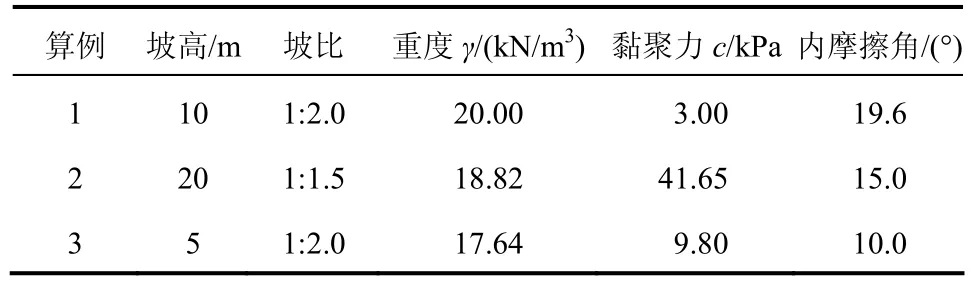
表1 算例1～3边坡参数Table 1 Slope parameters of examples 1-3

表2 均质边坡算例中最小安全安全系数对比Table 2 Contrast of the minimum FOS in homogeneous slope examples

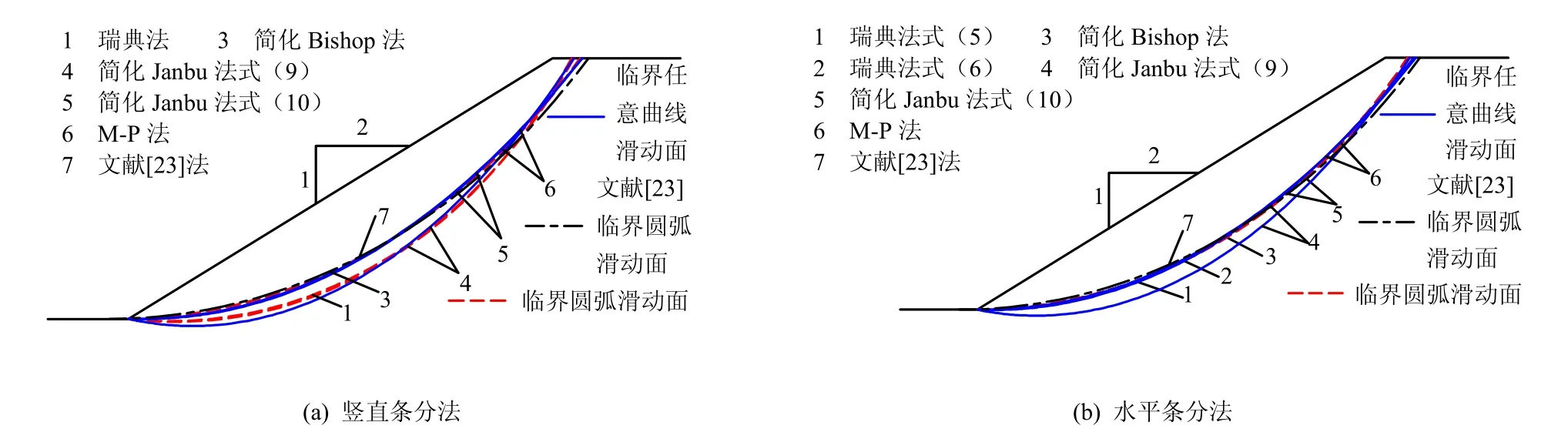
图6 算例1中的临界滑动面Fig.6 Critical sliding surfaces in example 1

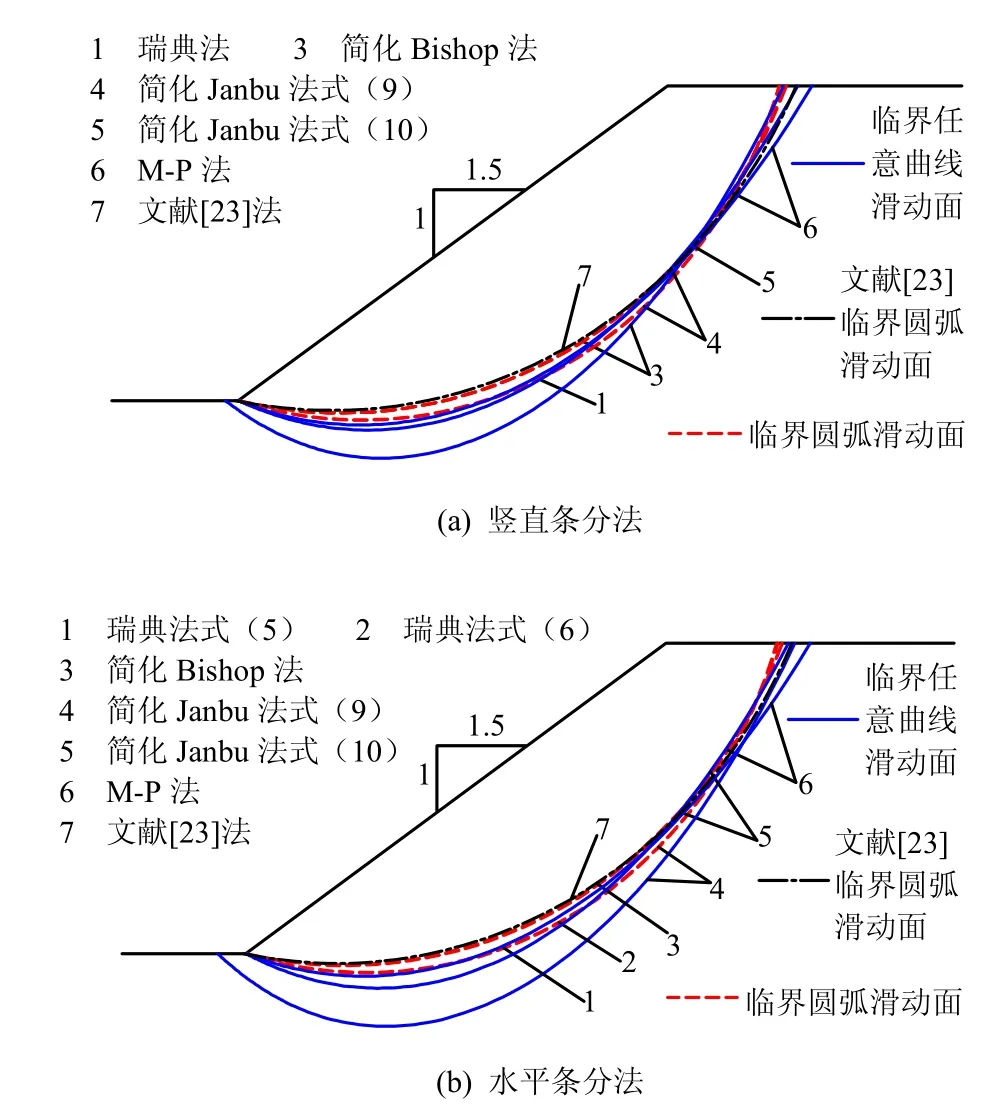
图7 算例2中的临界滑动面Fig.7 Critical sliding surfaces in example 2

图8 算例3中的临界滑动面Fig.8 Critical sliding surfaces in example 3

4.2 分层边坡

分别参考文献[1, 24－25]，选择3个算例进行对比分析，如图9～11所示。其中，对于任意曲线滑动面，采取文献[21]方法。

算例4：本边坡由3层水平土层组成，其下层为基岩。计算参数见表3。在文献[1]中，假定滑动面为圆弧滑动面时，瑞典法计算得的最小安全系数为1.321，Bishop法为1.355，Chen-M法为1.357，文献[1]法为1.367。

算例5：本边坡由2层土层组成，计算参数见表3。在文献[24]中，假定滑动面为螺旋线时，由刚体单元上限法得出的最小安全系数为1.01。

算例6：该边坡由2层水平土层组成，其计算参数见表3。在文献[25]中，假定滑动面为分段螺旋线时，通过极限上限分析法计算得的最小安全系数为1.000。

算例4～6计算得的最小安全系数见表4，得到的临界滑动面如图9～11所示。

表3 算例4～6边坡参数Table 3 Slope parameters of examples 4-6

表4 分层边坡算例中最小安全系数对比Table 4 Contrast of the minimum FOS in layered slope examples

从表4可知：在分层土坡中，本文水平条分法下的各方法计算得的安全系数与竖直条分法和文献方法相也非常接近，两种瑞典法计算得的安全系数也基本一致；改进的简化 Janbu法（即简化 Janbu法式（10））计算得的安全系数仍较一般简化Janbu法（即简化Janbu法式（9））优。

从图9～11可知：本文水平条分法和竖直条分法下各方法得到的临界滑动面（包括任意曲线滑动面和圆弧滑动面）与文献得到的临界滑动面相接近，临界任意曲线滑动面相似于圆弧滑动面，但表现为非圆弧型；水平条分法下两种瑞典法得到的临界圆弧滑动面仍基本相同。

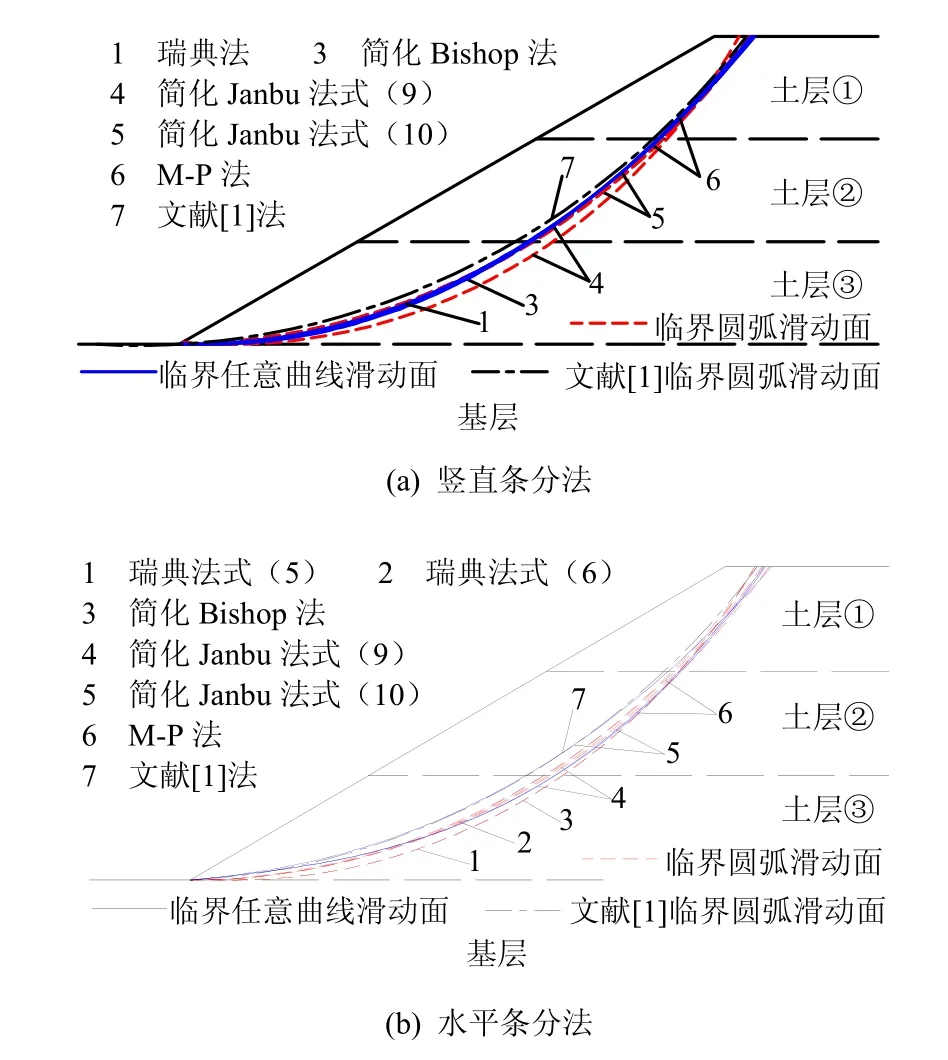
图9 算例4中的临界滑动面Fig.9 Critical sliding surfaces in example 4

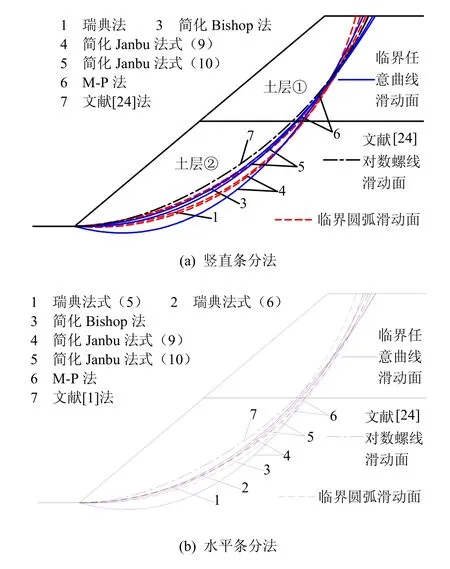
图10 算例5中的临界滑动面Fig.10 Critical sliding surfaces in example 5

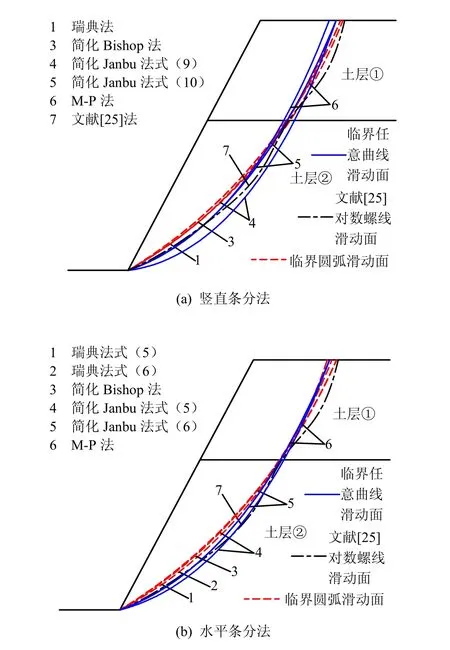
图11 算例6中的临界滑动面Fig.11 Critical sliding surfaces in example 6

5 结 论

（1）本文对水平条分和竖直条分中条间力的关系进行了分析，建立起水平条分法与竖直条分法相对应的条间力假设条件，并对水平条分遇到滑动面存在一段弓形体时，采用取斜条分与水平条分相结合模式，通过算例对比分析可知，文中各方法在水平条分时计算得的安全系数与竖直条分法和以往研究成果相接近，得到的临界滑动面也颇为相似，说明本文针对水平条分不足所采取的处理方法可行；

（2）任意曲线滑动面方法与圆弧滑动面方法计算得的安全系数接近，但较圆弧滑动面方法整体上偏小，且得到的临界滑动面与圆弧滑动面相似，但表现为非圆弧型；

（3）水平条分法中两种瑞典法计算得的安全系数和临界滑动面基本一致，竖直和水平条分法中一般Janbu法计算得的安全系数偏小，改进简化Janbu法计算得的安全系数与简化Bishop法和M-P法颇为接近，且改进简化Janbu法较一般Janbu法得到的临界滑动面与其他方法更接近一些。

参 考 文 献

[1]陈昌富, 杨宇. 边坡稳定性分析水平条分法及其进化计算[J]. 湖南大学学报(自然科学版), 2004, 31(3): 72－75.CHEN Chang-fu, YANG Yu. Horizontal slice method of slope stability analysis based on evolutionary algorithm[J].Journal of Hunan University(Natural Sciences), 2004,31(3): 72－75.

[2]朱大勇, 邓建辉, 台佳佳. 简化 Bishop法严格性的论证[J]. 岩石力学与工程学报, 2007, 26(3): 455－458.ZHU Da-yong, DENG Jian-hui, TAI Jia-jia. Theoretical verification of rigorous nature of simplified Bishop method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 455－458.

[3]朱大勇, 李焯芬, 黄茂松, 等. 对 3种著名边坡稳定性计算方法的改进[J]. 岩石力学与工程学报, 2005, 24(2):183－194.ZHU Da-yong, LEE C F, HUANG Mao-song, et al.Modifications to three well-known methods of slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 183－194.

[4]邹广电. 边坡稳定分析条分法的一个全局优化算法[J].岩土工程学报, 2002, 24(3): 309－312.ZOU Guang-dian. A global optimization method of the slice method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 309－312.

[5]万文, 曹平, 冯涛, 等. 基于加速混合遗传算法搜索复杂边坡的最危险滑动面[J]. 岩土工程学报, 2006, 28(4):475－479.WAN Wen, CAO Ping, FENG Tao, et al. Searching for the most dangerous failure surface of complex slope based on accelerating hybrid genetic algorithm[J].Chinese Journal of Geotechnical Engineering, 2006,28(4): 475－479.

[6]陈祖煜. 土坡稳定分析通用条分法及其改进[J]. 岩土工程学报, 1983, 5(4): 11－27.CHEN Zu-yu. The generalized method of slices for slope stability analysis and its modifications[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(4): 11－27.

[7]方玉树. 边坡稳定性分析条分法最小解研究[J]. 岩土工程学报, 2008, 30(3): 331－335.FANG Yu-shu. The lowest solution of slice method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(3): 331－335.

[8]吴振君, 葛修润. 求解边坡矢量和安全系数的条分法[J]. 岩土力学, 2009, 30(8): 2337－2342.WU Zhen-jun, GE Xiu-run. Solving vector sum factor of safety of slope by method of slices[J]. Rock and Soil Mechanics, 2009, 30(8): 2337－2342.

[9]童志怡, 陈从新, 徐健, 等. 边坡稳定性分析的条块稳定系数法[J]. 岩土力学, 2009, 30(5): 1393－1398.TONG Zhi-yi, CHEN Cong-xin, XU Jian, et al. A slice-stability method for stability analysis of slopes[J].Rock and Soil Mechanics, 2009, 30(5): 1393－1398.

[10]高玉峰, 范昭平. 多点、多向地震作用下非圆弧滑面边坡稳定分析通用条分法[J]. 岩土力学, 2010, 31(12):3816－3822.GAO Yu-feng, FAN Zhao-ping. Generalized slice method for stability analysis of slope with non-circular slide face under multipoint and multidirection seismic ground motions[J]. Rock and Soil Mechanics, 2010, 31(12):3816－3822.

[11]殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社,2007.

[12]BISHOP A W. The use of slip circle for the stability analysis of slopes[J]. Geotechnique, 1955, 5(1): 7－17.

[13]MORGENSTERN N R, PRICE V E. The analysis of the stability of general slip surfaces[J]. Geotechnique, 1965,15(l): 79－93.

[14]SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J].Geotechnique, 1967, 17(1): 11－26.

[15]陈昌富, 杨宇, 龚晓南. 基于遗传算法地震荷载作用下边坡稳定性分析水平条分法[J]. 岩石力学与工程学报,2003, 22(11): 1919－1923.CHEN Chang-fu, YANG Yu, GONG Xiao-nan.Horizontal slice method of slope stability analysis under seismic load based on genetic algorithm[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(11): 1919－1923.

[16]杨明成. 基于力平衡求解安全系数的一般条分法[J].岩石力学与工程学报, 2005, 24(7): 1216－1221.YANG Ming-cheng. A general slice method for determination of factors of safety based on force equilibrium[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1216－1221.

[17]SHAHGHOLI M, FAKHER A, JONES C J F P.Horizontal slice method of analysis[J]. Géotechnique,2001, 51(10): 881－885.

[18]NOURI H, FAKHER A, JONES C J F P. Development of horizontal slice method for seismic stability analysis of reinforced slopes and walls[J]. Geotextiles and Geomembranes, 2006, 24(3): 175－187.

[19]NOURI H, FAKHER A, JONES C J F P. Evaluating the effects of the magnitude and amplification of pseudo-static acceleration on reinforced soil slopes and walls using the limit equilibrium horizontal slices method[J]. Geotextiles and Geomembranes, 2008, 26(3):263－278.

[20]魏作安, 朱彬, 万玲, 等. 边坡锚固工程分析中的水平条分法[J]. 土木建筑与环境工程, 2010, 32(3): 53－56.WEI Zuo-an, ZHU Bin, WAN Lin, et al. Horizontal slice method for the stability analysis of reinforced slopes[J].Journal of Civil Architectural and Environmental Engineering, 2010, 32(3): 53－56.

[21]邓东平, 李亮, 赵炼恒. 基于 Janbu法的边坡整体稳定性滑动面搜索新方法[J]. 岩土力学, 2011, 32(3): 891－898.DENG Dong-ping, LI Liang, ZHAO Lian-heng. A new method of sliding surface searching for general stability of slope based on Janbu method[J]. Rock and Soil Mechanics, 2011, 32(3): 891－898.

[22]邓东平, 李亮, 赵炼恒. 稳定渗流条件下土坡稳定性分析的一种新方法[J]. 工程地质学报, 2011, 19(1): 29－36.DENG Dong-ping, LI Liang, ZHAO Lian-heng. A new method of stability analysis of slope under the condition of steady seepage[J]. Journal of Engineering Geology,2011, 19(1): 29－36.

[23]Rocscience Inc. Slide verification manual[R]. Toronto:Rocscience Inc., 2003.

[24]王根龙, 伍法权, 张军慧. 非均质土坡稳定性分析评价的刚体单元上限法[J]. 岩石力学与工程学报, 2008,28(增刊 2): 3425－3430.WANG Gen-long, WU Fa-quan, ZHANG Jun-hui. Upper bound approach of rigid elements for inhomogeneous soil slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 28(Supp. 2): 3425－3430.

[25]KUMAR J, SAMUI P. Stability determination for layered soil slopes using the upper bound limit analysis[J].Geotechnical and Geological Engineering, 2006, 24(6):1803－1819.