机构的多样性与创新设计的构思方法探究

2012-09-18王艳

滁州职业技术学院学报 2012年3期

王艳

（滁州职业技术学院，安徽滁州 239000）

随着科学技术的日益进步和计算机的广泛应用，现代机械在机构类型方面出现许多新的创造，正向着机-电-液-信息一体化方向发展，有些已突破了传统机构学范畴，进入“广义机构学”的领域。但是不论现代机械如何发展，传递和变换机械运动的系统的机构，仍然是多数机器的最重要组成部分[1]。设计实践表明，如果设计者具备机构分析与综合的现代理论知识，熟悉各种常用机构的性能、用途和设计要点，能从现有机构中发现规律并举一反三，就能在机械方案设计中取得主动。

一、机构创新的理论基础

机构是由具有确定相对运动的构件组合而成，是可以传递或变换机械运动的人工系统。机构要实现确定的相对运动，构件之间必然以运动副连接起来。由运动副联接而成的构件系统称为运动链。运动链分为闭式链和开式链。如果组成机构的每一个构件都为二副件，则称为单环机构，例如大家熟悉的铰链四杆机构等[2]。单环机构特点是构件总数N与运动副数P相等。如果在单环机构基础上叠加P-n=1（n为活动构件数）个运动链，则组成多环机构。多环机构的环数L=P-N+1。（式1）

二、机构创新设计的方法

（一）由杆组的组合获得多种机构

1、杆组及分类

平面机构包含原动件、机架和从动件系统，由于机构具有确定的相对运动的条件是机构的自由度等于原动件个数，所以剩下的从动件系统的自由度必然为零。从动件系统中不可再分的自由度为零的构件组称为杆组[4]。把若干个杆组依次联接到原动件和机架上，就组成一个新的机构，其自由度数与原动件数目相等。设组成杆组的构件数为n，低副数为PL，则其自由度为：F=3n-2PL=0。可见杆组中的构件数n必须是偶数，且当 n=2、4、6 时，PL=3、6，9。根据杆组的复杂程度，将杆组分成若干级别，机构的级别由组成该机构的杆组的最高级别而定。实际工程中所用的机构多数是II级机构。

2、平面机构的多样性构思-拆分后的杆组任意组合

如图1所示机构，计算机构的自由度F=1，并确定凸轮为原动件。根据拆分杆组的要领，先拆分出由构件4和5组成的Ⅱ级杆组，再拆分出由构件3和2及构件6和7组成的两个Ⅱ级杆组及由构件8组成的单构件高副杆组，最后剩下原动件1和机架9。机构多样性构思：只要取原动件1和机架9与上图中四个杆组中的任意一个或几个便组成各种类型的II级机构。由此可知，在原动件和机架上任意添加若干个杆组便可组成各种新的不同级别的机构，其自由度等于原动件个数，机构一定具有确定的相对运动。这是构思新机构的理论基础。

图1 杆组的拆分

（二）机构的变异

当机构型式不能较好实现预期运动要求，可以对原有机构进行创造性的变异。机构常用的变异方法有：

1、改变构件的局部结构

对于某些具有特殊运动特性的机构，可以通过改变构件的局部结构实现。如图2所示，在导杆机构原直线导槽上设置一段圆弧槽，其圆弧半径与曲柄长度相等，则导杆在左极限位置可以实现一段时间的停歇。这种变异使摆动导杆机构在往复摆动中实现一定的间歇运动。

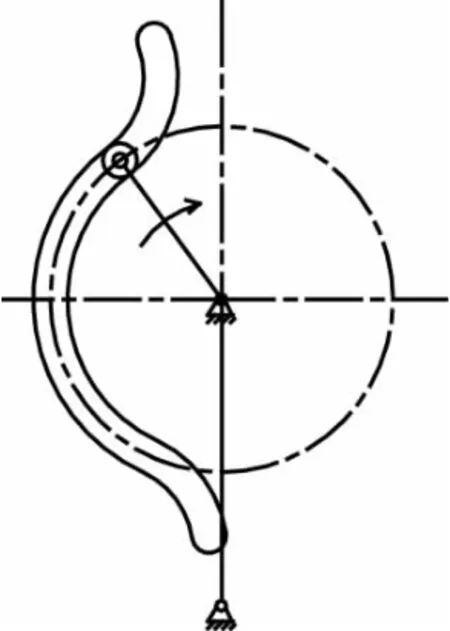
图2 有停歇的导杆机构

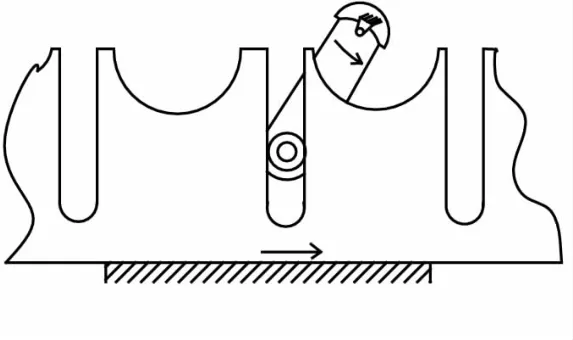
图3 槽轮展直得到槽条机构

2、改变构件的相对尺寸

改变构件的运动尺寸，会生成不同运动特性的机构。在转动导杆机构中，如果使机架长大于相邻杆长，则变为摆动导杆机构。又如图3所示，在槽轮机构中，如果槽轮的直径趋向无穷大，则槽轮展直而演变为槽条，于是槽轮机构就变异为图示的做间歇直线运动的槽条机构。

3、选不同的构件做机架

这种方法又称为机构的倒置。机构倒置后各构件之间的相对运动不变，但可以得到不同运动特性的机构[1]。例如曲柄摇杆机构，若改变机架位置，可得到双曲柄机构或双摇杆机构。又如曲柄滑块机构，取不同构件作机架可得到摆动导杆机构、曲柄摇块机构、移动导杆机构。再如，将内啮合齿轮机构的内齿轮作为机架，则可得到图4所示的行星轮系，从而增加了行星轮上不同点输出的轨迹形态。

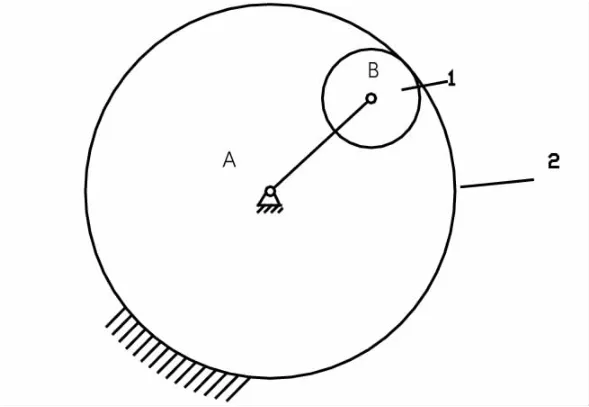
图4 内啮合齿轮机构的倒置机构

4、选不同的构件为原动件

在运用杆组法分析机构时可以看出：选择不同的原动件可得到不同级别的机构，一定程度体现了机构的多样性。多数机构中常取连架杆作为原动件，但在电风扇摇头机构中，原动件是连杆BC，连杆BC由蜗杆驱动，能做整周转动，驱动连架杆AB往复摆动，从而实现风扇的摇头。机构组成简单，构思巧妙。

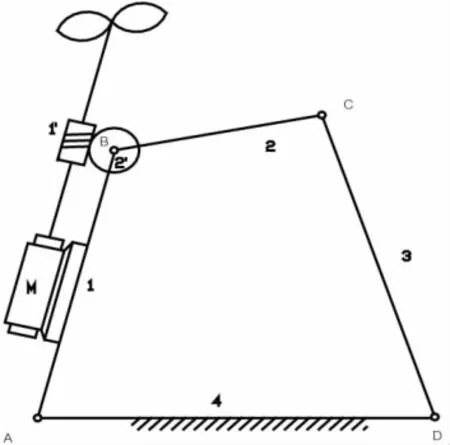
图5 电风扇摇头机构

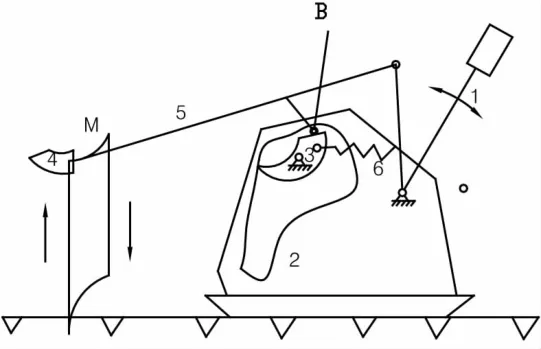
图6 手动插秧机的插秧机构

5、增加辅助构件

以原机构为基础，增加新的构件，生成新机构，各构件之间的相对运动关系不变，但新机构的性能与原机构有很大差别[1]。

图6的插秧机构中，在凸轮机构中增加了一个辅助构件活动舌3，当滚子B沿着凸轮左侧轮廓线向下运动时，活动舌的左端被滚子压开，滚子向下运动；当滚子离开活动舌后，弹簧6作用使活动舌恢复原位，使滚子向上运动时只能沿着右侧凸轮轮廓线。在通过活动舌右端时，又将其压开而上行，通过后，弹簧6又使活动舌恢复原位，滚子随后的运动只能继续向左下方进行。这样增加了活动舌后，秧爪下行和上行的路线不同，避免将已插好的秧苗带出。

（三）机构的“数综合”创新

研究一定数量的构件和一定类型的运动副，能组成某一自由度的运动链有多少种。这类问题属于机构结构综合“数综合”[2]。从这一定义而言，前面所述杆组的组合创新也归于数综合问题。这里主要研究平面闭式链数综合方法。

1、平面闭式链的基本型式

为便于说明问题，现只讨论仅含转动副，且自由度为1的平面闭式链机构，且不包含复合铰链。因机构自由度W=3(N-1)-2P（式2），式中N是总构件数，P是运动副数。若自由度为1，则有1=3(N-1)-2P，即3N=2P+4（式3），由式可知，构件总数N一定是偶数。常见的运动链有，(1)N=4，P=4;(2)N=6，P=7;(3)N=8，P=10;(4)N=10，P=13。将式（1）代入式（3），可以得出运动链环数L与构件总数N之间的关系：L=-1+N/2（式4）

2、常见机构的数综合结果

运用公式（4），对于四杆运动链，N=4，L=1，只有一个环，所以其可能的结构型式只有一种。六杆运动链，N=6，由式（4）知 L=2，即结构型式可能有两种，分别为瓦特型和斯蒂芬森型，这两种型式都可以认为是在四杆链上叠加双杆组而得。八杆运动链，N=8，L=3，可能的结构型式有16种。十杆运动链，L=4，分析知其可能的结构型式共有230种。

在上述平面运动链基本型式的基础上，如果采用不同构件为机架，或将转动副用移动副代替，以高副代替低副等方法，则可以得到多种多样的实际机构。

（四）机构的组合创新

随着生产的发展以及机械化、自动化程度的提高，单一的基本机构如连杆机构、齿轮机构和凸轮机构等往往不能满足要求。如齿轮机构、双曲柄机构和转动导杆机构虽能传递匀速和变速整周回转运动，但不能实现任意给定的运动规律的转动；而凸轮机构虽能实现任意规律的运动，但从动件不能实现整周转动。

由上可见，为了满足自动化、机械化生产发展的需要，就迫使人们去探索创造新的机构，以满足多种多样的运动要求和更加理想的动力性能要求。把若干个基本机构按照一定的方式组合起来形成组合机构是机构创新的重要途径。组合机构能使若干个基本机构融合成性能更加完善、运动形式更加多样化的新机构。代表性组合机构有：齿轮-连杆机构、凸轮-连杆机构、齿轮-凸轮机构等。