均质土中考虑溶质蜕变效应的污染物迁移模型的解析解

余 闯 方冬芳 杜广印 陈樟龙 蔡晓庆 徐江伟

(1温州大学防灾减灾工程研究所，温州 325035)

(2东南大学岩土工程研究所，南京 210096)

均质土中考虑溶质蜕变效应的污染物迁移模型的解析解

余 闯1，2方冬芳1杜广印2陈樟龙1蔡晓庆1徐江伟1

(1温州大学防灾减灾工程研究所，温州 325035)

(2东南大学岩土工程研究所，南京 210096)

针对一些有机污染物溶质具有蜕变的性质，建立了均质土中考虑污染物蜕变的一维迁移模型，采用分离变量法获得了模型的解析解.典型算例计算结果表明，上述模型的计算结果与经典的GAEA Pollute分析软件的计算结果基本一致，说明了该方法的正确性和可靠性.通过对该模型的参数进行讨论分析发现:考虑蜕变效应对计算结果有一定影响;随着污染物半衰期的减小，污染程度急剧降低;扩散系数对计算结果存在较大影响，准确获取该参数对提高预测精度至关重要.提出的解析方法可用于预测具有蜕变性质污染物的迁移规律，从而为相关填埋场垫层设计提供参考.

污染物;迁移;蜕变;解析解

近年来，随着我国工农业的迅速发展，化学污染物质源源不断地向生态系统释放，由此导致了严重的土壤污染.一些原来被工业企业占用甚至污染的土地需要进行二次开发利用［1］.在工程建设过程中，由于对土地污染问题认识不足及污染清除和污染土处理工作不到位，造成了一些污染事件.理论分析污染物在土体中的迁移规律是评价污染场地的重要手段.近年来，国内外学者对污染物的迁移规律开展了大量的研究工作，并取得了一定的进展.

污染物在土介质中的迁移规律受很多因素的影响［2］，主要有对流、弥散、分子扩散、蜕变及吸附等.一般认为同时考虑对流、弥散和蜕变项的迁移模型［3-5］能较好地反映实际情况.很多学者通常采用对流-弥散模型来模拟污染物的迁移规律［6-8］.在一般渗流速率很小的情况下，分子扩散作用在污染物迁移中占主导地位，一些学者直接采用弥散模型来模拟污染物迁移问题的研究［9-11］.张金利等［8］考虑到单层土中废弃物与防渗层接触面处的浓度分布随时间的变化近似地服从指数衰减关系，推导出了污染物迁移的一维数值解，但未考虑污染物迁移过程中的生物降解和蜕变等效应.

本文针对分子扩散作用占主导地位的情况，并根据部分有机污染物本身可发生蜕变的特点，建立了考虑蜕变的污染物扩散模型;继而采用分离变量法获取了上述模型的解析解.通过对解析解的编程分析计算，得到了考虑污染物蜕变后的一些结果，并将计算结果与经典数值计算结果进行了对比分析.

1 污染物扩散模型

本文建立的考虑污染物蜕变影响的土中污染物一维扩散模型主要基于以下假设:① 土层为均质、饱和的;②介质中阻滞因子和有效扩散系数是常数，不随时间、空间变化;③ 污染物扩散是一维的，并且污染物源在土层上部，不考虑其他外部污染源;④渗滤液中污染物的扩散仅由污染物的溶度梯度引起，忽略水力传导的作用，同时考虑土颗粒对污染物的线性吸附作用;⑤ 考虑污染物扩散过程中的蜕变影响.

在上述基本假设的前提下，简化污染物在土壤中的迁移方程［2］，得到了污染物的一维扩散模型，如图1所示.污染物的扩散方程为

式中，C(z，t)为土层中的污染物浓度，mg/L;R为土对污染物的阻滞因子;D为土中污染物的扩散系数，m2/s;λ为土中污染物的蜕变系数，这里λ=ln2/t1/2，t1/2为污染物衰变的半衰期;z为深度，m;t为时间，a.

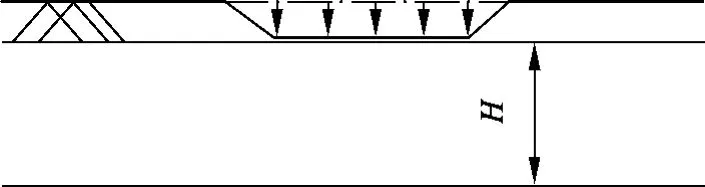
图1 污染物一维扩散剖面图

根据文献［4］，模型的边界条件可表示为

假设在有污染源之前，该土层没有被污染，故本模型的初始条件可描述为

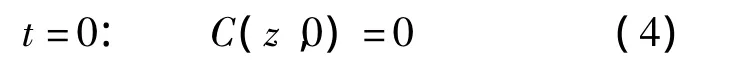
2 模型求解

为了求解方便，把非齐次边界条件的定解问题转化为另一未知函数的齐次边界条件定解问题.利用叠加原理，令

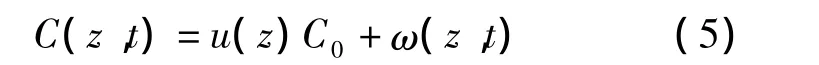
将式(5)代入(1)，得

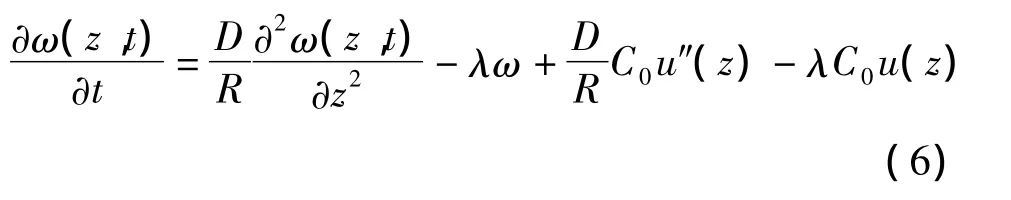
式(6)的求解可转化为以下2个定解问题进行求解，分别描述如下:

定解问题1

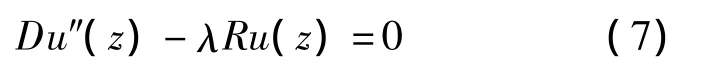
边界条件

定解问题2

边界条件

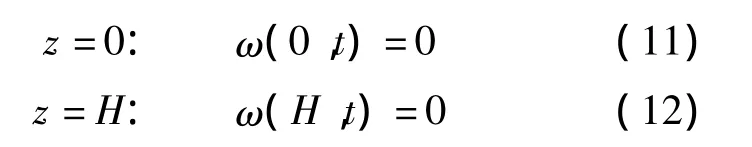
初始条件

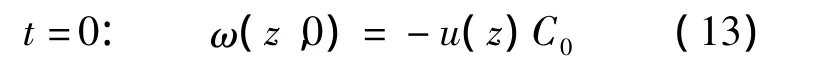
下面求解定解问题1.由式(7)可解得

式中，r21=λR/D.由边界条件式(8)、(9)推得

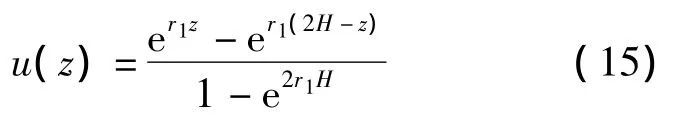
下面求解定解问题2.设

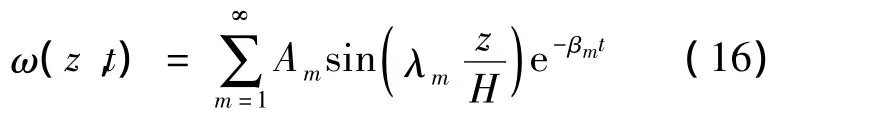
式(16)满足上边界条件式(11)、(15).将式(16)代入式(10)可得

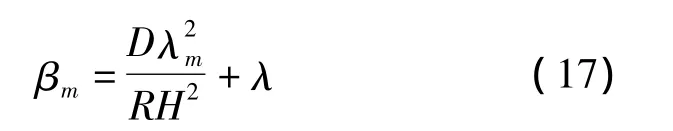
由下边界条件式(11)可得

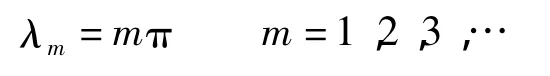
由正交函数的正交性质可知

由初始条件式(13)知

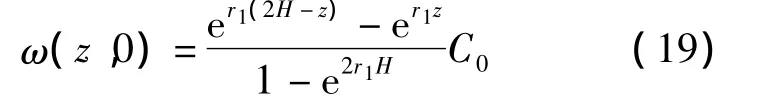
所以求得

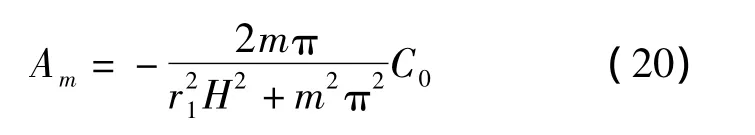
将以上所求系数代入式(16)，即得ω(z，t).至此，可求得C(z，t)的解，如下所示:

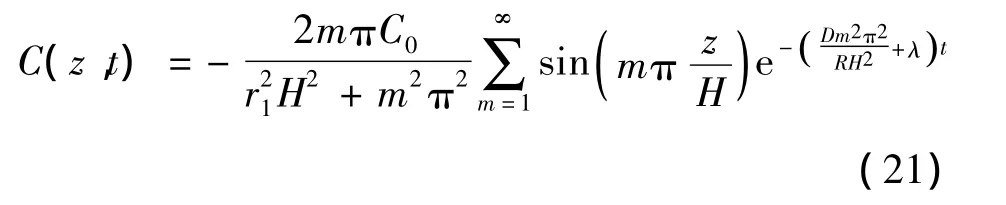
进一步可求得污染物的通量为

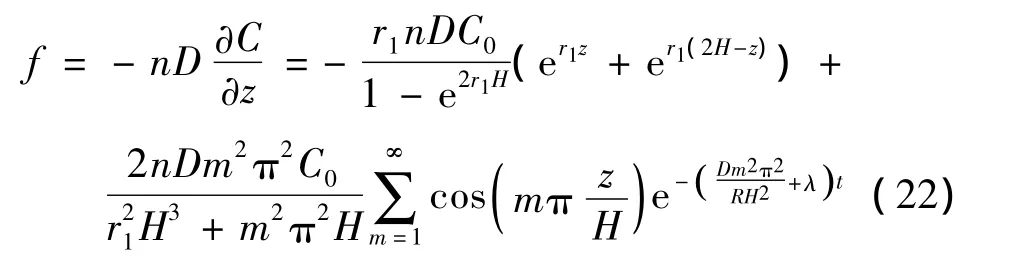
3 算例分析与应用

基于求得的解析解，编制了计算程序，对考虑蜕变的污染物的迁移规律进行了算例分析，边界条件为顶部浓度1.0，底部浓度0.基本参数取值如表1所示.GAEA Pollute V7是一款专业的污染物迁移分析程序，被广泛用于垃圾填埋设计和环境评估等领域.将该软件1.5维度的解决方案运用到对流-扩散方程中.软件计算得出的结果和本文推导的理论结果进行对比，结果如图2和图3所示.

表1 土层的物理化学性质参数［9］

图2给出了考虑污染物半衰期为50 a和不考虑蜕变2种方法计算得到的污染物30，60和120 a这3个时间点下浓度沿深度的分布曲线，从图中可看出，本文理论解得到的污染物浓度分布曲线与GAEA Pollute得到的分布规律较为一致，吻合得较好，这也证明了本文理论解的可靠性和正确性.另外从2个图对比可看出，考虑蜕变与不考虑蜕变，计算结果差别较大，其中D0=6.5 ×10－11m2/s.

图2 理论计算与数值模拟结果对比分析

基于本文推导的理论解，获取了不同参数情况下污染物浓度分布规律，如图3所示.由图3(a)可看出，随着半衰期的缩短，污染物的浓度急剧下降，其影响深度也急剧降低;由图3(b)可发现，扩散系数对计算结果影响很大，因此准确地获取该参数是提高计算精度的关键;由图3(c)可发现，不同的阻滞因子对计算结果有较大的影响，随着阻滞因子的增加，污染影响深度在加大;图3(d)给出了不同深度处污染物浓度随时间的分布曲线.

图3 各参数对计算结果的影响

4 结语

针对一些有机污染物溶质具有蜕变的性质，利用土中污染物的蜕变系数，建立了均质土中考虑溶质蜕变的污染物迁移一维计算模型，采用分离变量法求解得到了解析解.基于解析解编写了相关的程序，并将典型算例与经典的GAEA Pollute软件的计算结果进行了对比分析，两者结果基本一致，证明了本文所提方法的可靠性和正确性.

通过参数讨论分析发现，考虑蜕变对计算结果影响较大，随着半衰期的减小，污染物浓度急剧降低;扩散系数对计算结果影响也很大，准确地获知该参数对于提高预测精度至关重要.本文提出的考虑蜕变性质的污染物迁移计算方法，可为有关填埋场垫层设计提供参考.本文模型是在基于土体对污染物的线性吸附的假设上建立的，考虑非线性吸附以及地基成层性的影响问题有待进一步深入研究.

［1］杜延军，金飞，刘松玉，等.重金属工业污染场地固化/稳定处理研究进展［J］.岩土力学，2011，32(1):116-124.

Du Yanjun，Jin Fei，Liu Songyu，et al.Review of stabilization/solidification techniqueforremediation of heavy metals contaminated lands［J］.Rock and Soil Mechanics，2011，32(1):116-124.(in Chinese)

［2］ Chen Y G，Ye W M，Xie Z J，et al.Remediation of saturated Shanghai sandy silt contaminated with p-xylene using air sparging［J］.Natural Hazards，2012，62(3):1005-1020.

［3］叶为民，金麒，黄雨，等.地下水污染试验研究进展［J］.水利学报，2005，36(2):251-255.

Ye Weimin，Jin Qi，Huang Yu，et al.Review on advance in experimental study of pollution dispersion in groundwater［J］.Journal of Hydraulic Engineering，2005，36(2):251-255.(in Chinese)

［4］ Rowe R K，Quigley R M，Brachman R W L，et al.Barrier systems for waste disposal［M］.London:Spon Press，2004.

［5］查甫生，许龙，崔可锐.水泥固化重金属污染土的强度特性试验研究［J］.岩土力学，2012，33(3):652-657.

Zha Fusheng，Xu Long，Cui Kerui.Strength characteristics of heavy metal contaminated soils stabilized/solidified by cement［J］.Rock and Soil Mechanics，2012，33(3):652-657.(in Chinese)

［6］郑春苗.地下水污染物迁移模拟［M］.北京:高等教育出版社，2009.

［7］Rowe R K，Booker J R.The analysis of pollutant migration in a non-homogeneous soil［J］.Geotechnique，1984，34(4):601-612.

［8］张金利，栾茂田，杨庆.固体废弃物生物降解时污染物运移过程一维数值分析［J］.大连理工大学学报，2004，44(6):870-875.

Zhang Jinli，Luan Maotian，Yang Qing.One-dimensional numerical analyses of pollutant migration process in solid waste considering bio-degradation effect of contaminants［J］.Journal of Dalian University of Technol-ogy，2004，44(6):870-875.(in Chinese)

［9］陈云敏，谢海建，柯翰，等.层状土中污染物的一维扩散解析解［J］.岩土工程学报，2006，28(4):521-524.

Chen Yunmin，Xie Haijian，Ke Han，et al.Analytical solution of contaminant diffusion through multi-layered soils［J］.Chinese Journal of Geotechnical Engineering，2006，28(4):521-524.(in Chinese)

［10］谢海建，唐晓武，陈云敏，等.原始土层影响下成层介质污染物一维扩散模型［J］.浙江大学学报:工学版，2006，40(12):2191-2195.

Xie Haijian，Tang Xiaowu，Chen Yunmin，et al.One-dimensionalmodelfor contaminantdiffusion through layered media［J］.Journal of Zhejiang University:Engineering Science，2006，40(12):2191-2195.(in Chinese)

［11］ Chen Yunmin，Xie Haijian，Ke Han.An analytical solution for one-dimensional contaminant diffusion through multi-layered system and its applications［J］.Environ Geol，2009，58(5):1083-1094.

Analytical solution on pollutant migration considering solute decay in homogeneous soil

Yu Chuang1，2Fang Dongfang1Du Guangyin2Chen Zhanglong1Cai Xiaoqing1Xu Jiangwei1

(1Institute of Engineering Disaster Prevention and Mitigation，Wenzhou University，Wenzhou 325035，China)
(2Institute of Geotechnical Engineering，Southeast University，Nanjing 210096，China)

Due to the decay of some organic pollutants solute，a one-dimensional computational model is established to calculate the migration of pollutants in the homogeneous soil.The separation of variables method is used for solving the analytical solution and the corresponding program is made to give the solution.A typical case study is conducted for verification of the presented method.The calculation results keep consistent with the results from classic software GAEA Pollute，which proves the reliability and validity of the proposed method.Through the parameters study，it is found that the decay has an important impact on the calculation results，and the pollutant concentration is drastically reduced with the decrease of the half-life.Diffusion coefficient has a great impact on the calculation results，so an accurate value of the diffusion coefficient is important to improve the prediction accuracy.The analytical solution can be used to predict pollutant migration considering the decay of pollutants，which can provide a reference for the landfill liner design.

pollutants;migration;decay;analytical solution

X53

A

1001－0505(2012)06-1206-05

10.3969/j.issn.1001 －0505.2012.06.033

2012-06-13.

余闯(1977—)，男，博士，副教授，3945735@qq.com.

国家自然科学基金资助项目(41002091)、浙江省“新世纪151人才工程”专项资金资助项目、温州市国际合作项目(H20100047).

余闯，方冬芳，杜广印，等.均质土中考虑溶质蜕变效应的污染物迁移模型的解析解［J］.东南大学学报:自然科学版，2012，42(6):1206-1210.［doi:10.3969/j.issn.1001 －0505.2012.06.033］