砂土中吸力式沉箱基础的最大承载力计算方法

黎 冰 高玉峰 沙成明 童小东

(1东南大学土木工程学院，南京 210096)

(2河海大学海岸灾害及防护教育部重点实验室，南京 210098)

(3河海大学岩土工程研究所，南京 210098)

砂土中吸力式沉箱基础的最大承载力计算方法

黎 冰1，2高玉峰3沙成明3童小东1

(1东南大学土木工程学院，南京 210096)

(2河海大学海岸灾害及防护教育部重点实验室，南京 210098)

(3河海大学岩土工程研究所，南京 210098)

为了准确确定砂土中吸力式沉箱基础的最大承载力，应用极限平衡法对其进行分析.基于吸力式沉箱基础平动时的受力特点，充分考虑土压力和摩擦力的发挥过程以及沉箱横截面上各点土压力大小的不同，提出了一种计算砂土中吸力式沉箱基础最大承载力的三维极限平衡方法.方法中假定沉箱侧壁土压力满足Winkler模型，但其值不超过水平极限土压力值;假定沉箱侧壁与地基土之间的摩擦力在达到最大值之前与两者之间的相对位移成线性正比关系.开展了15组水平荷载作用下吸力式沉箱基础的模型试验，得到了吸力式沉箱基础的荷载-位移曲线.利用所提方法得到的计算结果与模型试验结果吻合较好，说明该方法是准确有效的.

吸力式沉箱基础;承载力;极限平衡法;砂土;平动

吸力式沉箱基础是一种底端敞开、上端封闭的大直径钢质圆桶结构，在深水海洋平台工程中的应用越来越多.深水海洋平台中的吸力式沉箱基础承受的是拉拔荷载，确定并充分发挥其抗拔能力是工程设计中的关键问题.

目前，吸力式沉箱基础承载力的计算方法大多是针对黏土地基的，针对砂土地基的研究很少.Bang等［1-2］提出了一种计算砂土中吸力式沉箱基础承载力的极限平衡方法，通过引入渐变的摩擦角来考虑土体摩擦力随基础位移发展而逐渐发挥的过程;但由于渐变的摩擦角随基础转动中心位置的改变会发生较大变化，故计算时需要考虑的基础破坏模式种类较多，计算较复杂.孙曦源等［3］针对黏土地基中的吸力式沉箱基础，提出了一种三维极限平衡计算方法，方法中假定沉箱外壁和底部的土压力均服从Winkler假定，但没有考虑土体所能提供的极限抗力以及基础外壁水平方向上的摩擦力.

已有研究表明，外荷载作用下吸力式沉箱基础发生平动时的抗拔承载力最大［1，4-6］.目前尚未见专门针对平动条件下吸力式沉箱基础承载力的计算方法.因此，本文在前人研究基础上，提出了一种计算砂土中吸力式沉箱基础最大承载力的三维极限平衡方法.

1 计算模型与假定

计算模型如图1所示.沉箱长度为L，直径为D，在荷载P作用下发生沿x轴方向的水平平动.为推求吸力式沉箱基础的最大承载力，进行如下假定:①坐标系采用右手坐标系，x轴平行于纸面向右为正，y轴垂直于纸面向外为正，z轴平行于纸面向下为正，应力、力与坐标轴正向一致为正，弯矩以顺时针为正;② 将沉箱与其内部的土体视为一个刚性整体;③忽略主动区域的土压力，仅考虑被动区域的土压力作用.作用在沉箱外壁上的土压力服从Winkler假定，但不超过极限土压力值.

图1 计算模型示意图

2 计算方法推导

2.1 外壁径向土压力

如图2所示，当沉箱在x方向产生位移u时，外壁上任意点处水平位移的径向分量为

式中，θ为计算点和沉箱横截面圆心的连线与荷载作用线的夹角(锐角).

图2 沉箱外壁任意点位移分解图示

根据Winkler假定，吸力式沉箱基础外侧径向土压力为

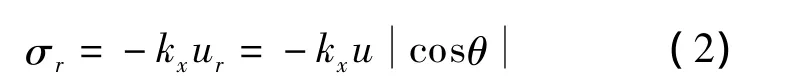
式中，kx为水平方向地基系数.根据文献［7］可知，kx可由下式计算得到:

式中，d为计算点深度，m;x0为沉箱顶泥面处沿x方向的水平位移，此处x0=u，m;nh为地基反力系数，N/m3;nhmax为剪应变小于0.002时的最大水平地基反力常数，可从Murchison等［8］提出的砂土地基水平反力初始模量与相对密实度的关系图中查得(见图 3)，N/m3.

根据文献［7，9］的研究可知，砂土地基中土压力的极限值为

图3 地基反力初始模量与相对密实度的关系图［7］

式中，Kp为被动土压力系数，且Kp=tan2(45°+φ'/2)，其中 φ'为砂土的有效内摩擦角;γ'为土体有效重度.

作用在吸力式沉箱基础外壁上的土压力σra取Winkler模型计算得到的σr与极限值σrmax中的较小值，即

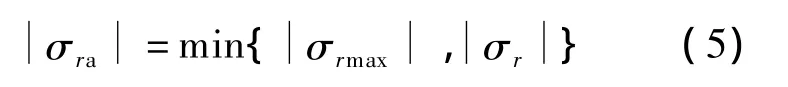
因此，任一点所受径向土压力在x方向的分量为

2.2 外壁摩擦力

假定最大摩擦力等于该点正应力与沉箱-土之间摩擦角正切值的乘积，即

式中，τmax为极限摩擦力;δ为基础与砂土地基的界面摩擦角.根据Kulhawy等［10-11］的研究可知，光滑的钢制材料与砂土之间的摩擦角可取为砂土有效内摩擦角的0.5～0.7倍;粗糙的混凝土材料与砂土之间的摩擦角可取砂土有效内摩擦角的1.0倍;光滑的混凝土材料与砂土之间的摩擦角可取砂土有效内摩擦角的0.8～1.0倍.

据Bourles［12］的研究可知，作用在沉箱侧壁上的摩擦力在达到最大值之前，摩擦力大小与沉箱-土界面的相对位移成正比;当界面相对位移达到某一界限值ul后，摩擦力达到最大值并保持不变.沉箱外壁上任意点水平切向位移uτ可由下式计算得到

对应的水平向摩擦力ττ为

2.3 底部水平摩擦力

当沉箱水平平动时，沉箱底面内外砂土之间发生错动，类似砂土直剪试验.故假定当相对位移较大时，摩擦力达到最大值并等于砂土抗剪强度τbmax;当相对位移较小时，仍假定摩擦力与水平位移成正比，取水平位移界限值u2=6 mm［13］.则有

当 ττ≥τmax时，取 ττ= τmax.

摩擦力在x方向的分量为

式中，τb为沉箱底面内外砂土间的摩擦力.

当 τb≥τbmax时，取 τb= τbmax.

基于上述分析，由x方向静力平衡条件可得

利用式(1)～式(13)编制计算程序，即可求得吸力式沉箱基础发生任一水平位移时所对应的水平荷载，并可绘制出吸力式沉箱基础平动时的荷载-位移曲线.程序中需输入的参数有kx，D，L，φ'，nhmax，ul.

3 方法验证

为了验证本文方法的准确性，通过模型试验研究了水平荷载作用下吸力式沉箱基础的抗拔承载特性.试验用土为砂土，粒径集中于0.075～1.000 mm，其有效重度为8.9 kN/m3，有效内摩擦角为36.8°，制样干密度为 1.44 g/cm3，相对密实度为49%.地基土总厚度为1.0 m，分10层填筑，每层厚度约为0.1 m.将干砂称重后倒入模型槽内，压实至预设高度、抹平.填土完成后，将设在模型槽底部的进水阀打开，使水在土体中自由向上渗透，土体饱和完成后保持水面在泥面以上约0.02 m.沉箱模型直径D=0.101 m，长径比L/D分别为2，4，6，荷载水平作用于沉箱上.荷载作用点共5个，分别位于沉箱顶点以及距离沉箱顶面L/2，2L/3，3L/4，L处.试验中采用分级加载的方式，每级荷载为沉箱模型预估承载力的1/10.

通过模型试验发现，当荷载水平作用于沉箱的2L/3处时，沉箱发生与加载方向一致的前倾转动;当荷载水平作用于沉箱的3L/4处时，沉箱发生与加载方向相反的后倾转动.具体的荷载-沉箱转角关系见图4.由图可知，当荷载水平作用于沉箱的2L/3或3L/4处时，沉箱转动角度均较小.模型试验中很难准确找到吸力式沉箱基础刚好发生平动时的荷载作用点;但根据荷载作用于2L/3处时沉箱前倾、3L/4处时沉箱后倾可以推断，吸力式沉箱基础发生平动的水平荷载作用点位于沉箱高度的2/3～3/4之间.

根据砂土的相对密实度，查图3可得nhmax=15 MN/m3.吸力式沉箱基础与砂土之间的摩擦角取砂土有效内摩擦角的0.6倍.计算沉箱外壁摩擦力时，取界面相对位移界限值ul=8 mm.利用本文方法可求得模型试验中3种工况下吸力式沉箱基 础的荷载-位移曲线，结果见图5.

图4 荷载与吸力式沉箱转角关系曲线

图5 吸力式沉箱基础的荷载-位移试验曲线

由图5可知，从荷载-位移曲线的发展趋势看，模型试验得到的曲线与应用本文方法计算得到的曲线较为接近.若以位移值达到沉箱直径的20%作为吸力式沉箱基础的破坏标准［14］，那么从承载力大小的角度来看，计算值大约是试验值(取2个试验值中的大值)的1.2倍.由前述分析已知，荷载水平作用于沉箱高度的2/3～3/4处时，沉箱转动角度较小，接近于平动.但图5中的荷载-位移试验曲线并不是吸力式沉箱基础发生平动时的荷载-位移曲线，根据已有研究成果［1，4-6］可知，基础发生平动时的承载力必定要比由图5中的荷载-位移试验曲线确定的承载力稍大，因此计算值比试验值稍大是合理的.此外，受模型试验条件的限制，很难准确确定吸力式沉箱基础刚好发生平动时的荷载作用点，因此本文未能得到吸力式沉箱基础发生平动时的荷载－位移曲线，故而无法确定计算值比荷载作用点位于沉箱高度2/3和3/4处时的试验值大于20%这一结论是否正确.

4 结语

本文提出了一种计算砂土中吸力式沉箱基础最大承载力的三维极限平衡方法.该方法全面考虑了吸力式沉箱基础平动时外壁所受的土压力、摩擦力和沉箱底部所受的摩擦力，并根据吸力式沉箱基础直径大的特点，充分考虑了土压力和摩擦力的发挥过程以及沉箱横截面上各点土压力大小不同的特性.利用该方法得到的计算结果与模型试验结果吻合较好，说明本方法是合理的.

［1］ Bang S，Cho Y.Ultimate horizontal loading capacity of suction piles［C］//Proceedings of the11th International Offshore and Polar Engineering Conference.Stavanger，Norway，2001:552-559.

［2］Bang S，Jones K D，Kim K O，et al.Inclined loading capacity of suction piles in sand［J］.Ocean Engineering，2011，38(7):915-924.

［3］孙曦源，栾茂田，唐小微.饱和软黏土地基中桶形基础水平承载力研究［J］.岩土力学，2010，31(2):667－672.

Sun Xiyuan，Luan Maotian，Tang Xiaowei.Study of horizontal bearing capacity of bucket foundation on saturated soft clay ground ［J］.Rock and Soil Mechanics，2010，31(2):667－672.(in Chinese)

［4］Clukey E C，Aubeny C P，Murff J D.Comparison of analytical and centrifuge model tests for suction caissons subjected to combined loads［J］.Journal of Offshore Mechanics and Arctic Engineering，2004，126(4):364-367.

［5］ Sukumaran B，McCarron W O，Jeanjean P，et al.Efficient finite element techniques for limit analysis of suction caissons under lateral loads［J］.Computers and Geotechnics，1999，24(2):89-107.

［6］ Supachawarote C，Randolph M F，Gourvenec S.The effect of crack formation on the inclined pull-out capacity of suction caissons［C］//Proceedings of the11th International Association for Computer Methods and Advances in GeomechanicsConference. Turin， Italy，2005:577-584.

［7］ Zhang L.Nonlinear analysis of laterally loaded rigid piles in cohesionless soil［J］.Computers and Geotech-nics，2009，36(5):718-724.

［8］Murchison J M，O’Neill M W.Evaluation of p-y relationships in cohesionless soils［C］//Proceedings of a Symposium in Conjunction with the ASCE National Convention on Analysis and Design of Pile Foundations.San Francisco，California，USA，1984:174-191.

［9］ Fleming W G K，Weltman A J，Randolph M F，et al.Piling engineering［M］.2nd ed.New York:Surrey University Press，1992.

［10］ Kulhawy F H，Trautmann C H，Beech J F，et al.Transmission line structure foundations for uplift-compression loading［R］.Palo Alto:Electric Power Research Institute，1983.

［11］ Kulhawy F H.Drilled shaft foundations［M］.New York:Van Nostrand Reinhold，1991:537-552.

［12］ Bourles J E.Foundation analysis and design［M］.5th ed.New York:The McGraw-Hill Companies，Inc.，1996.

［13］中华人民共和国水利部.GB/T 50123—1999土工试验方法标准［S］.北京:中国计划出版社，1999.

［14］Kumar N D，Rao S N.Earth pressures on caissons in marine clay under lateral loads—a laboratory study［J］.Applied Ocean Research，2010，32(1):58-70.

Calculation method for maximum bearing capacity of suction caisson foundation in sand

Li Bing1，2Gao Yufeng3Sha Chengming3Tong Xiaodong1

(1School of Civil Engineering，Southeast University，Nanjing 210096，China)
(2Key Laboratory of Coastal Disasters and Defence of Ministry of Education，Hohai University，Nanjing 210098，China)
(3Research Institute of Geotechnical Engineering，Hohai University，Nanjing 210098，China)

To accurately determine the maximum pull-out loading capacity of suction caisson foundation in sand，the limit equilibrium method is applied.Based on the mechanical characteristics of suction caisson foundation with horizontal translation，a method for three-dimensional limit equilibrium analysis of maximum pull-out loading capacity of suction caisson foundation in sand is proposed.In the proposed method，the development process of earth pressure and shear resistance with displacement，and the characteristics of different earth pressure and side shear resistance over the caisson cross-section are considered.The earth pressure acting on the caisson is assumed to obey the Winkler model and is not in excess of the limiting earth pressure.The shear resistance between caisson and soil is assumed to be linearly proportional to the relative displacement between them before reaching its ultimate value.Fifteen model tests of suction caisson foundation under horizontal loading in sand are conducted to investigate its pull-out behaviors，and the load-displacement curves are obtained.The calculation results by the proposed method agree well with the experimental results，indicating that the proposed method is accurate and effective.

suction caisson foundation;bearing capacity;limit equilibrium;sand;horizontal translation

TU47

A

1001－0505(2012)06-1201-05

10.3969/j.issn.1001 －0505.2012.06.032

2012-07-09.

黎冰(1981—)，男，博士，讲师，lbershui@seu.edu.cn.

国家自然科学基金资助项目(50909020，51078082)、海岸灾害及防护教育部重点实验室开放研究基金资助项目.

黎冰，高玉峰，沙成明，等.砂土中吸力式沉箱基础的最大承载力计算方法［J］.东南大学学报:自然科学版，2012，42(6):1201-1205.［doi:10.3969/j.issn.1001 －0505.2012.06.032］