加固加层隔震结构阻尼比特性的振动台试验

刘 鑫 刘伟庆 王曙光 杜东升

(南京工业大学土木工程学院，南京 211816)

加固加层隔震结构阻尼比特性的振动台试验

刘 鑫 刘伟庆 王曙光 杜东升

(南京工业大学土木工程学院，南京 211816)

利用振动台试验研究了由砌体、混凝土加固墙板、顶部隔震钢框架组成的复杂结构的阻尼比特性.首先，建立了5层加固、加层不隔震以及加层隔震3种试验模型;然后，利用特征系统实现算法(ERA)对这3种模型的扫频数据进行模态拟合，识别试验模型在不同地震波输入量级下的结构阻尼比，并分析其随地震波输入量级的变化规律.试验结果表明，对于非隔震结构，随着地震波输入量级的增加，结构发生刚度退化，结构阻尼比增加;对于加层隔震结构，随着地震波输入量级的增加，隔震层下部的砌体结构损伤不断累积，使得上部结构与下部结构的刚度比增加，整体结构的一阶阻尼比减小，二阶阻尼比增加.试验数据分析所得的3种试验模型的阻尼比变化规律与现有理论分析结果一致.该试验结果为由不同材料组成的不同结构体系在地震作用下的阻尼比取值提供了相关依据及参考.

加固加层隔震结构;阻尼比;振动台试验;刚度比

随着建筑形式的多样化，已经和将要建造的包含不同阻尼特性材料的组合结构越来越多［1］.我国抗震设计规范［2］规定:对于特别不规则的建筑、甲类建筑和特定高度范围的高层建筑，宜采用时程分析法进行多遇地震下的补充计算.时程分析中必然涉及阻尼取值的问题.阻尼取值稍不合理，便会产生较大的计算误差［3］.对于不同材料组成的结构阻尼，研究者们采用复振型方法进行分析，取得了较满意的结果［4-5］;但由于复振型方法非常复杂，缺少相应的结构计算软件配合，故难以应用于实际结构的计算中.文献［6-7］采用强迫解耦的方法，利用经典阻尼理论，对非比例阻尼结构进行分析，结果表明:当结构阻尼比较小时，结果误差较小;当阻尼比较大时，结果误差较大.此外，还存在很多计算结构阻尼比的方法，例如单元阻尼比法［8］、子结构瑞雷阻尼法［9］等，但这些计算方法都是基于大量的假设基础上的.目前，对于由不同阻尼材料组成的复杂结构，如何确定其阻尼比等参数以及在地震作用下阻尼比的变化，仍没有较好的理论和方法.

同时，研究者们通过试验对结构材料的阻尼特性进行了研究.Chung等［10］开展了针对基底隔震结构的振动台试验以及一系列拟动力试验，研究了结构阻尼比在地震耗能中的作用.Cheng等［11］利用振动台试验研究了桥梁在不同量级地震动作用下的阻尼比变化，试验结果与理论分析结果一致.然而，这些研究大多都针对的是单一材料所组成的结构，对于不同阻尼性质材料组成的结构在地震响应下的阻尼比试验研究还比较少.

砌体结构是一种传统的墙体材料.根据历次地震后砌体结构震害的调查分析可知，这种结构在震害中受到破坏较大.閤东东等［12］提出了一种基于装配式技术的加固体系，以提高老旧住宅抗震性能.这种基于装配式技术的加固体系是由砌体、钢筋混凝土、钢材等具有不同阻尼性质的材料组合而成的，其结构整体阻尼比参数难以确定.同时，该结构采用层间隔震技术，以减小上部加层钢结构对整体结构抗震性能带来的不利影响，因而导致整体结构在地震作用下的阻尼比变化更加复杂.

本文对加固加层隔震结构进行了振动台试验研究.利用DASP信号采集及数据处理装置对试验模型的地震响应数据进行采集分析，采用特征系统实现算法［13］识别试验模型在不同工况下的阻尼比，并对试验模型在不同输入量级下的阻尼比变化进行了研究.

1 加层隔震试验模型阻尼比的变化规律

在现场试验与强震观测中早已发现，结构物的自振特性一般会随振幅大小而改变，通常表现为地震前的微振幅振动测得的自振周期最短，阻尼最小.在大震之后，即使采用小振幅振动进行测量，结构的自振周期较地震前测得的结果明显增长.这是由于结构在经历强烈地震后出现了轻重不同的损坏，使得结构的刚度减小.

本文中的加层隔震振动台试验模型下部为外套钢筋混凝土的砌体加固结构，上部为钢结构，地震作用下的阻尼比变化更加复杂.将此加层隔震试验模型模拟成两自由度系统，运动方程可描述为

式中

式中，md，ms分别为隔震支座下侧砌体加固结构和上侧钢结构的集中质量;kd，ks分别为砌体加固结构的弹性刚度和隔震支座的有效刚度;cd，cs分别为砌体加固结构的黏性阻尼系数和隔震支座的等效黏性阻尼系数;ud，us分别为砌体加固结构顶部大梁和上部钢结构相对于地面的侧向位移;ug为地面的侧向位移.

可以看出，式(1)中的阻尼矩阵为非比例阻尼矩阵，不能分解为对角阵.运动方程是耦合的，利用状态空间列式法对运动方程进行解耦.定义如下状态向量:

式(1)给出的运动方程可化简为一阶状态空间方程的形式，即

式中

假设系统矩阵A的复固有特征值为λn，且

式中分别为结构第n阶阵型的自振频率与阻尼比.

由此可知

利用下式求解矩阵A的特征值

将式(9)展开可得

解出式(10)中的λn后，即可利用式(7)、(8)确定结构各阶阵型的自振频率ωn与阻尼比ζn.

杨佑发等［14］以底层框架上部砖房的层间隔震结构为研究对象，利用上述的理论推导估算了不同参数对结构组合阻尼比的影响，重点讨论了整体结构的一、二阶阻尼比随结构刚度比的变化规律.结果表明，层间隔震的组合阻尼比与隔震支座的有效刚度和下部结构的弹性刚度之比Rd密切相关.随着结构损伤的加剧，上、下部结构的刚度比逐渐减小，整体结构的一阶阻尼比增加，二阶阻尼比减小.随着结构上部阻尼比的增加，这种变化规律变得更加明显.

2 模拟地震振动台试验

2.1 模型设计与制作

本试验包括3个试验模型，分别为5层砌体加固模型A、加固加层模型B和加固加层并隔震模型C.模型A为5层砌体结构外套钢筋混凝土加固;模型B在模型A的顶部加入2层钢框架，并通过栓钉与下部混凝土连接.模型C在模型B的上部钢框架与下部加固结构之间增加了隔震层.试验所用的加速度传感器布置在各模型的每层楼板上，底层布置在基座上，用以记录台面的加速度输入.试验模型及加速度传感器的具体布置示意图分别见图1和图2.

图1 振动台试验模型

图2 传感器布置

试验模型砌体部分的平面尺寸为1.50 m×2.25 m，第1层层高为0.75 m，第2～5层层高均为0.70 m，砌体部分高度为3.55 m.砌体结构砌筑于现浇混凝土底座上，通过底座与振动台基座连接.混凝土底座尺寸为 2.06 m ×3.25 m ×0.30 m，按照弹性地基梁的方式设计，外套加固混凝土强度等级为C30.5层加固结构自重为10.42 t，配重为5.15 t.

钢框架共分 2层，平面尺寸为 1.50 m×3.13 m，层高分别为 0.54 和 0.85 m.采用 Q235钢，柱和梁分别选择尺寸为40 mm×40 mm×4 mm和40 mm×30 mm×3 mm的方钢管.长向边柱下端点焊20 mm厚带螺栓孔的钢垫，通过高强螺栓与隔震支座相连.沿钢框架长向每层各布置4根尺寸为30 mm×4 mm的角钢制备的柱间支撑，以提高其在长向的刚度.7层隔震结构自重为11.46 t，配重为 6.50 t.

试验橡胶隔震支座采用6个低弹性铅芯支座.每个隔震支座的竖向刚度为106 MN/mm，有效刚度keq=110 N/mm，屈服力Qy=300 kN(屈重比约为4%)，模型与原型的相似比结果见表1.

表1 模型与原型相似比

2.2 试验工况及加载顺序设计

本试验采用3种地面地震运动(El Centro波、Taft波和人工波)作为输入.振动台试验分别考虑了未加层结构模型、加层隔震结构模型和加层非隔震结构模型.试验加载工况按照7度多遇、8度多遇、7度基本烈度(250和375 cm/s2)、8度基本烈度以及8度罕遇顺序分阶段进行.

对5层加固、加层不隔震以及加层隔震3种模型进行振动台试验.考虑到试验着重研究加层隔震体系的抗震性能，对每个模型进行初始扫频及小震工况输入后，在保证试验模型没有发生明显损伤的情况下，首先对加层隔震模型进行中震及大震工况的输入.在地震波输入量级达到1 000 cm/s2时，试验模型的2层砌体墙出现了沿灰缝的较长裂缝;结构发生明显损伤后，加固墙板根部也出现了细微的水平裂缝(见图3).

图3 结构损伤裂缝开展图

加层隔震结构试验工况结束后，移走隔震垫，将上部钢框架与下部砌体加固结构通过螺栓连接，输入加层不隔震结构的中震工况荷载.然后，将上部钢框架移走，输入5层加固结构的中震工况荷载.具体加载顺序见表2.

表2 试验模型加载顺序

3 阻尼比分析

采用峰值为70 cm/s2的白噪声对结构进行扫频，利用DASP V10型振动台试验数据采集分析装置进行试验模型地震反应数据的采集与分析，识别3种试验模型在不同工况下的各阶频率及阻尼比.

DASP系统采用特征系统实现算法(ERA法)进行模态拟合.其基本思想为:首先，根据系统的脉冲响应数据，构造Hankel矩阵;然后，对该矩阵进行奇异值分解，根据分解结果得到该系统的最小实现状态矩阵;最后，对该矩阵进行特征值分解，得到系统的动力参数.

分别在每组工况加载前，对3种试验模型进行白噪声扫频，识别其动力特性.不同量级的地震荷载作用后试验模型A，B，C的一、二阶频率及阻尼比识别结果分别见表3～表5.

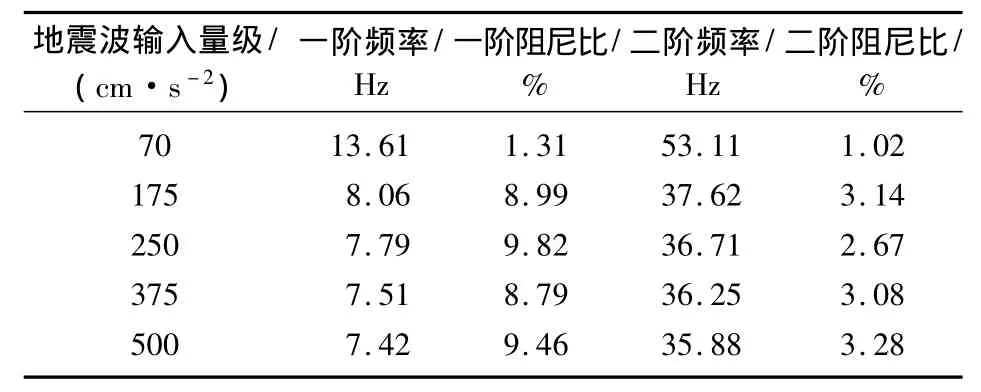
表3 不同地震波输入量级下模型A的频率及阻尼比变化

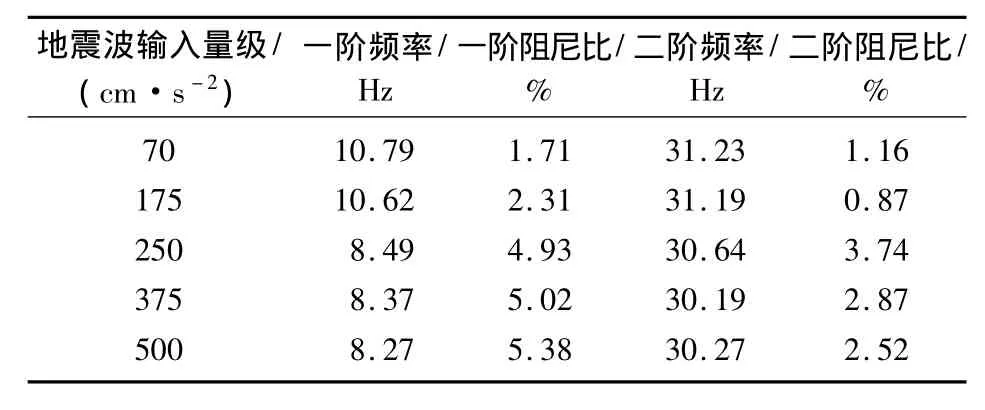
表4 不同地震波输入量级下模型B的频率及阻尼比变化

表5 不同地震波输入量级下模型C的频率及阻尼比变化

由表3和表4可知，随着输入地震波量级的增加，5层加固试验模型和加层不隔震试验模型的一、二阶频率均有所减小，但其一阶阻尼比增加.结合试验过程和图4可以更为直观看出，2层砌体墙在加层隔震结构受到1 000 cm/s2地震作用时发生了严重破坏，下部加固结构的刚度发生严重退化，阻尼比明显增加.7度中震(250 cm/s2)输入下5层加固结构及加层不隔震结构的阻尼比较小震输入时有了明显增加，这是由于结构在经历强烈地震后，裂缝的发展使得结构的阻尼比显著增加.

随着振动台地震波输入量级的增加，加层隔震试验模型的下部结构进入非线性反应，结构刚度逐渐退化，上部结构与下部结构的刚度比逐渐增加.由表5及图4可知，随着地震波输入量级的增加，加层隔震结构的一阶阻尼比逐渐减小，二阶阻尼比逐渐增加.特别是在震波输入量级达到1 000 cm/s2时，下部砌体结构发生较大损坏，结构刚度明显退化，上部结构与下部结构的刚度比显著增加，结构的整体阻尼比变化明显.由理论分析可知，加层隔震结构的一、二阶阻尼比和隔震层上部与下部结构的刚度比密切相关，一阶阻尼比随着上部与下部结构刚度比的增加而减小，二阶阻尼比则随之增加.该理论结果与试验现象一致.

图4 3种试验模型的阻尼比变化

4 结论

1)对5层加固结构、加层不隔震结构以及加层隔震结构进行了振动台试验研究.对试验模型进行信号采集及数据处理分析，结果表明，随着地震波输入量级的增加，非隔震结构的刚度发生退化，自振频率减小，阻尼比增加.对于加层隔震结构而言，随着地震波输入量级的增加，下部结构首先进入非线性反应，结构刚度不断减小.尤其在地震波输入量级达到1 000 cm/s2时，下部砌体墙出现明显裂缝，结构刚度退化明显，隔震层上部与下部结构的刚度比显著增加，整体结构的一阶阻尼比减小，二阶阻尼比增加.试验结果与理论分析一致.

2)对于由砌体和钢筋混凝土2种不同材料所组成的5层加固结构，随着地震波输入量级的增加，其阻尼比也逐渐增加.结构进入弹塑性反应阶段后，阻尼比可达9.46%，相比弹性反应阶段(1.31%)增加了近8倍.

3)对于由砌体、钢筋混凝土及钢材3种不同材料所组成的加层不隔震结构，随着地震波输入量级的增加，阻尼比也逐渐增加.但是，由于钢框架的阻尼比较小，与5层砌体加固结构相比，该结构的整体阻尼比有所减小.结构进入弹塑性反应阶段后，阻尼比达到5.38%.

4)在地震波输入量级未达到1 000 cm/s2之前，加层隔震结构的自振频率与阻尼比变化不大，表明隔震层上部与下部结构的刚度比变化不大.其原因可能是层间隔震体系使得结构的地震反应减轻，结构刚度退化不明显.因此，这种层间隔震结构可有效降低结构的地震反应.

［1］段绍伟，向湘林，沈蒲生.复杂阻尼结构阻尼模型研究［J］.振动与冲击，2011，30(2):73-76.

Duan Shaowei， Xiang Xianglin， Shen Pusheng.Damping model of a complex structure［J］.Journal of Vibration and Shock，2011，30(2):73-76.(in Chinese)

［2］中华人民共和国住房和城乡建设部.GB50011—2010建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.

［3］ Ducan P E，Taylor E R.A note on the dynamic analysis of non-proportional damped systems［J］.Earthquake Engineering and Structural Dynamics，1979，7(1):99-105.

［4］Novak M，Hifnaway L E.Effect of soil-structure-interaction on damping of structure［J］.Earthquake Engineering and Structural Dynamics，1983，11(5):595-621.

［5］刘庆林，傅学怡，孙占琦.基于复阻尼假定的不同材料阻尼特性混合结构抗震分析复模态叠加法［J］.建筑结构学报，2011，32(9):27-33.

Liu Qinglin，Fu Xueyi，Sun Zhanqi.A complex mode superposition method for seismic analysis of structures of multiple material damping characteristics based on complex damping assumption［J］.Journal of BuildingStructures，2011，32(9):27-33.(in Chinese)

［6］Berman A，Nagy E Y.Improvement of a large analytical model using test data［J］.The American Institute of Aeronautics and Astronautics Journal，1983，21(8):1168-1173.

［7］俞瑞芳，周锡元.非比例阻尼弹性结构地震反应强迫解耦方法的背景和数值检验［J］.工业建筑，2005，35(2):52-56.

Yu Ruifang，Zhou Xiyuan.Theoretical and numerical research on forced uncoupling method for seismic response of non-classically damped linear system［J］.Industrial Construction，2005，35(2):52-56.(in Chinese)

［8］淡丹辉，孙利民.结构动力有限元的模态阻尼比单元阻尼建模法［J］.振动、测试与诊断，2008，28(2):100-103.

Dan Danhui，Sun Limin.Damping modeling and its evaluation based on dynamical analysis of engineering structure by finite element method［J］.Journal of Vibration，Measurement＆Diagnosis，2008，28(2):100-103.(in Chinese)

［9］ Clough R W，Penzien J.Dynamics of structures［M］.2nd ed.Berkeley，California，USA:Computer and Structures，Inc.，1995:237-242.

［10］ Chung Woo-Jung，Yun Chung-Bang.Shaking table and pseudo-dynamic tests for the evaluation of the seismic performance of base-isolated structures［J］.Engineering Structures，1999，21(4):365-379.

［11］ Cheng Chin-Tung.Shaking table tests of a self-centering designed bridge substructure［J］.Engineering Structures，2008，30(12):3426-3433.

［12］閤东东，陈曦，苗启松，等.砌体结构房屋加固足尺实验模型数值模拟［J］.土木工程与管理学报，2011，28(3):344-348.

Ge Dongdong，Chen Xi，Miao Qisong，et al.Numerical research on a full-scale masonry building retrofitted by external precast structure［J］.Journal of Civil Engineering and Management，2011，28(3):344-348.(in Chinese)

［13］顾培英，邓昌，吴福生.结构模态分析及其损伤诊断［M］.南京:东南大学出版社，2008:79-82.

［14］杨佑发，王立福，王功.在非比例阻尼情况下层间隔震底层框架砖房的组合阻尼比［J］.工业建筑，2003，33(12):47-49.

Yang Youfa，Wang Lifu，Wang Gong.On calculation of the non-proportional damping effect for the interlayer isolation masonry building with frame structure in the first storey［J］.Industrial Construction，2003，33(12):47-49.(in Chinese)

Shaking table test of damping ratio of strengthening-adding-story isolation structures

Liu Xin Liu Weiqing Wan Shuguang Du Dongsheng
(College of Civil Engineering，Nanjing University of Technology，Nanjing 211816，China)

The damping ratio of a complex structure composed of masonry，concrete reinforced wall and isolation steel framework was studied by shaking table tests.First，three test models，five-story strengthening structure，strengthening-adding-story structure and strengthening-adding-story isolation structure，were set up.Then，the sweeping date of these three models were fitted by the eigensystem realization algorithm(ERA).The damping ratios of these test models were identified under the different levels of the ground motions and the variation of damping ratios with the increase of the ground motions were studied.The experimental results show that，with the increase of ground motions，the stiffness of the non-isolated structure decreases while the damping ratio of the structure increases.For the mid-story isolation structure，the damage of masonry accumulates gradually with the increase of ground motions，inducing the increase of the stiffness ratio between superstructure and substructure，the decrease of the first-order damping ratio and the increase of the second-order damping ratio of the structure.The development trends of the damping ratio of these three test models are accorded with the theoretical analysis.The experimental results provide basis and reference for choosing proper damping ratios for different structure systems with different materials.

strengthening-adding-story isolation structures;damping ratio;shaking table test;stiffness ratio

TU399

A

1001－0505(2012)06-1151-06

10.3969/j.issn.1001 －0505.2012.06.024

2012-03-15.

刘鑫(1988—)，男，博士生;刘伟庆(联系人)，男，博士，教授，博士生导师，wqliu@njut.edu.cn.

国家自然科学基金资助项目(50908115，51178219)、江苏省普通高校研究生科研创新计划资助项目(CXLX12_0438).

刘鑫，刘伟庆，王曙光，等.加固加层隔震结构阻尼比特性的振动台试验［J］.东南大学学报:自然科学版，2012，42(6):1151-1156.［doi:10.3969/j.issn.1001 －0505.2012.06.024］