异径混合非球形颗粒在移动床中流动特性的数值模拟

陶 贺 钟文琪 金保昇 任 冰 袁竹林

(1郑州航空工业管理学院土木建筑工程系，郑州 450000)

(2东南大学能源与环境学院，南京 210096)

异径混合非球形颗粒在移动床中流动特性的数值模拟

陶 贺1钟文琪2金保昇2任 冰2袁竹林2

(1郑州航空工业管理学院土木建筑工程系，郑州 450000)

(2东南大学能源与环境学院，南京 210096)

为了研究非球形颗粒在移动床内的流动特性，采用多元颗粒模型模拟了异径玉米形颗粒、异径椭球形颗粒以及异径圆柱形颗粒在移动床中的流动情况.探讨了异径混合球形和非球形颗粒在移动床中流动时的流型、概率分布特性以及空隙率分布情况.结果表明:异径球形颗粒在下料过程中由整体流逐渐向漏斗流转变，而异径非球形颗粒从下料开始即为漏斗流;异径球形颗粒及非球形颗粒的概率密度分布中均只有一个峰值，其对应的速度不同;异径圆柱形混合颗粒的空隙率波动范围最大，平均空隙率也最大;异径混合非球形颗粒的直径比越大，平均空隙率越小.

多元颗粒模型;非球形颗粒;移动床;流动特性

移动床技术具有颗粒可循环再生、操作可连续进行等优点，广泛应用于石化、环保和能源等领域.床内颗粒的流动规律对床层压降、床层渗透性、气体线性速度等有很大影响，是影响移动床结构设计及效率的重要因素.但由于床内颗粒物料流动的复杂性，颗粒物料的流动规律很难预测.目前针对移动床内颗粒流动的研究较多［1-8］，但大多数都是针对球形颗粒的，对非球形颗粒流动特性的研究很少.实际应用中，大部分颗粒都是非球形颗粒，例如移动床反应器内用于烟气净化的活性焦颗粒就是典型的圆柱形颗粒，在模拟研究的过程中，如果用球形颗粒来近似代替，势必会产生较大误差，并且活性焦颗粒在移动床中流动时容易磨损甚至破碎，使得床内颗粒由大小相同的均质颗粒变成了直径不同(异径)的混合颗粒.因此，对非球形颗粒尤其是异径混合非球形颗粒的模拟研究显得十分重要.

本文采用离散元直接数值模拟(DEM)方法，对异径混合非球形颗粒(异径玉米形颗粒、异径椭球形颗粒和异径圆柱形颗粒)在移动床中的流动进行了模拟研究.从数值模拟的角度揭示了异径混合非球形颗粒的流动规律，为移动床反应器的设计及结构参数优化提供参考.

1 数学模型及实验验证

本文采用多元颗粒模型［9-13］来描述非球形颗粒.每个非球形颗粒均由几个叠放在一起的球组成，这些球被称为元.图1为玉米形颗粒、椭球形颗粒及圆柱形颗粒的模型示意图.用DEM方法模拟颗粒流动最关键的问题在于如何掌握颗粒的碰撞机理并建立颗粒的运动方程，关于这些问题，在前期所做的工作［14］中有详细的描述.

图13种非球形颗粒的模型示意图(单位:mm)

在实验验证方面，本文所采用的移动床的床体横截面积为200 mm×200 mm，高度为600 mm，出口尺寸为45 mm×45 mm，下料段与水平面的夹角θ=60°.实验中3种形状的物料分别采用玉米、黑豆和活性焦.实验前移动床出口闭合，床层为重力作用下自然堆积的静止填充床.将出口打开，颗粒在重力作用下从床内卸出，并向移动床顶部不断加料，保证床内物料流动连续.当床内物料流动稳定时，向床内加入示踪粒子.图2和图3分别为玉米形颗粒、椭球形颗粒和圆柱形颗粒连续加料下料时流型的实验结果和模拟结果.由图可知，利用DEM方法得到的模拟结果与实验结果吻合良好.因此，本文所建立的数学模型是合理的.

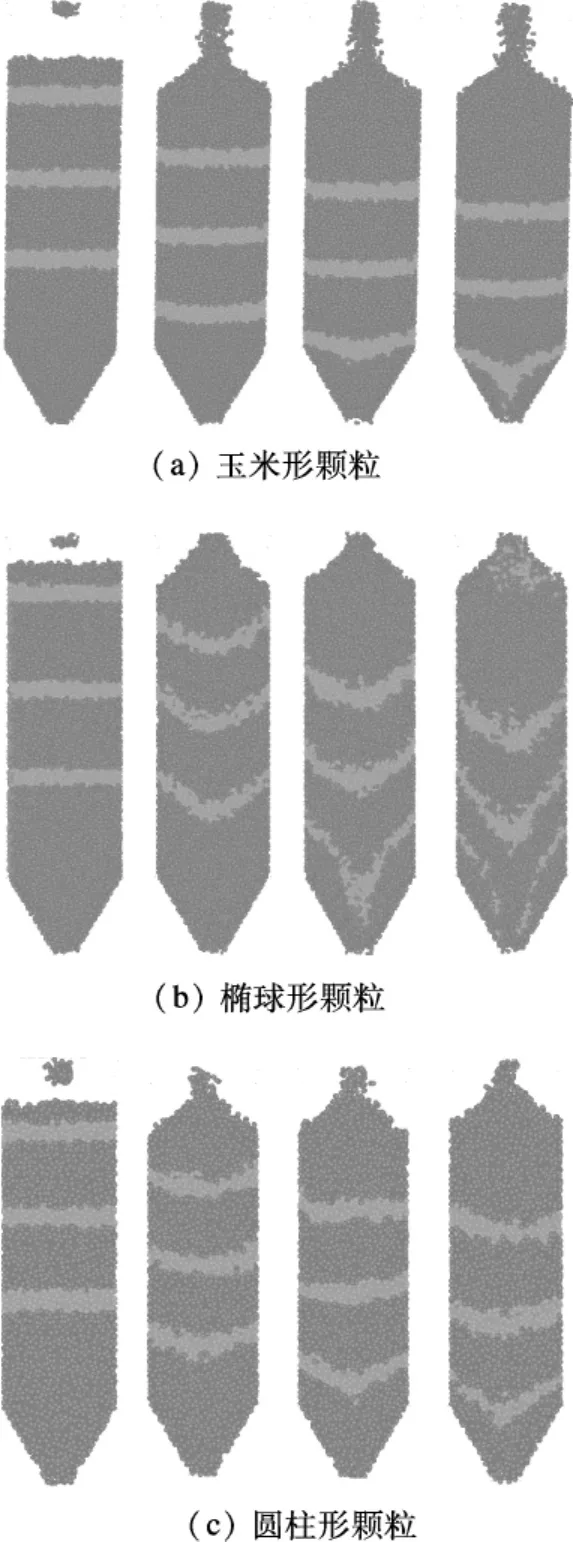
图2 3种非球形颗粒流型的模拟结果

2 结果与讨论

2.1 异径混合非球形颗粒的流型

颗粒在移动床内的流动主要有2种形式:整体流和漏斗流.一般情况下，开始时颗粒以整体流的形式向下流动，之后慢慢转变成漏斗流.为了定量地分析卸料过程中移动床内颗粒何时从整体流向漏斗流转变以及各种非球形颗粒流型的不同之处，定义了流动指数MFI，即壁面附近颗粒的平均速度与中心处颗粒平均速度之比.壁面附近颗粒和中心处颗粒平均速度的计算区域见图4.假设边壁处计算区域的宽度为颗粒直径d，中心处计算区域的宽度为2d;此时颗粒直径是指球形颗粒的直径，本文中的椭球形颗粒则采用当量直径.计算区域的厚度即为床宽.根据 Johanson［15］的研究可知，MFI值为0.3时，整体流开始向漏斗流转变;MFI值大于0.3时，颗粒流动为整体流;MFI值小于0.3时，则为漏斗流.

图3 3种非球形颗粒流型的实验结果

图4 中心和边壁处平均速度的计算区域

图5为异径混合颗粒的流型比较.需要指出的是，本文中所用的颗粒直径比φD是指同种颗粒2种粒径之比，且2种粒径的颗粒均是按照体积比1∶1进行混合的.由图5(a)可知，球形混合颗粒在下料初始过程中，MFI值大于0.3，呈现出整体流的流动状态;随着卸料的进行，MFI值逐渐减小;当下料率达到41%时，整体流向漏斗流转变.其他3种异径非球形混合颗粒的MFI值明显小于球形.异径椭球形混合颗粒在卸料初始阶段的MFI值最大，其次是玉米形混合颗粒，异径圆柱形混合颗粒的MFI值最小.随着下料率的进一步增大，3种形状混合颗粒的MFI值逐渐减小，且玉米形混合颗粒的MFI值最大，其他2种颗粒的MFI值相似.由此可知，非球形颗粒从颗粒开始流动时便为漏斗流，其原因可能是非球形颗粒受形状的限制，滚动性较差.

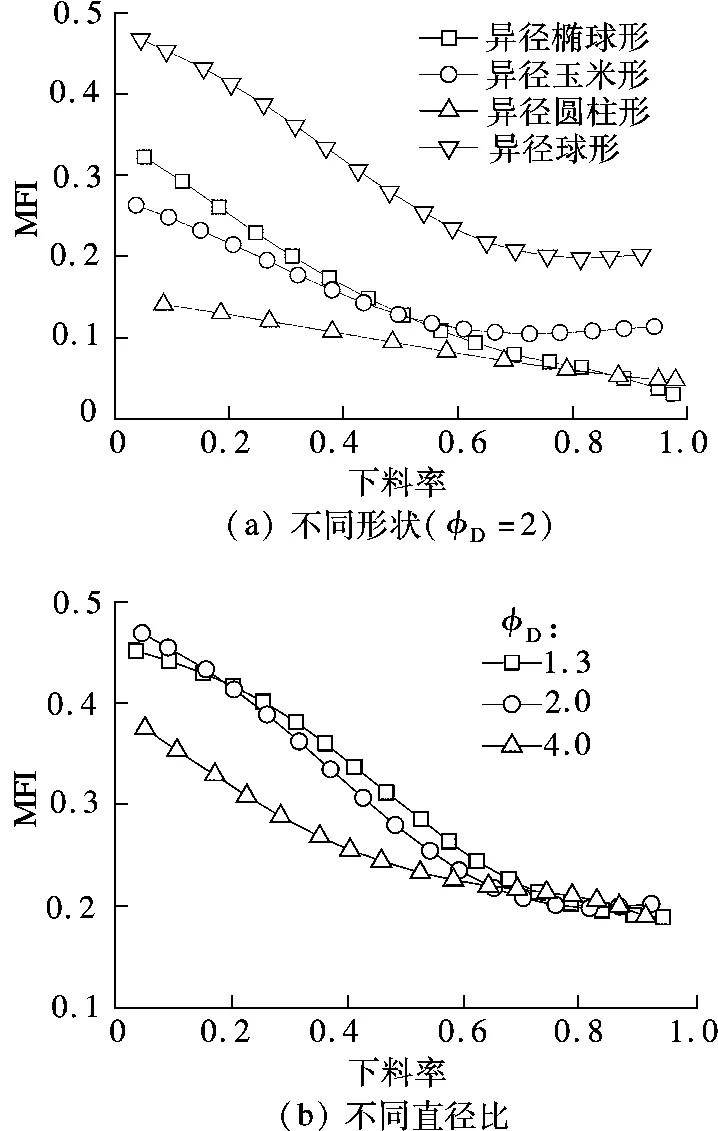
图5 异径混合颗粒的流型比较

不同颗粒直径比的球形混合颗粒的流型比较见图5(b).由图可知，当 φD=1.3，2.0 时，MFI值相差很小.但当 φD=4.0时，MFI值明显减小，且当下料率为0.25时，球形混合颗粒的流型由整体流向漏斗流转变.

2.2 异径混合非球形颗粒的概率分布特性

定义概率密度ρ=Nx/Nt来描述移动床内颗粒速度的分布［16］，其中Nt表示移动床内颗粒的总数，Nx表示速度处于某一值时的颗粒数.因此，ρ表示速度处于某一值时的颗粒数量与总颗粒数量之比.

图6为异径混合颗粒的概率分布情况.由图6(a)可知，当φD=1.3时，概率分布的峰值为0.36，对应的速度值为0.15 m/s;当φD=2时，概率分布的峰值为0.32，对应的速度值为0.1 m/s;当φD=4时，概率分布的峰值为0.25，对应的速度值为0.05 m/s.因此，颗粒直径比越小，速度分布范围越窄;反之，颗粒直径比越大，速度分布范围越宽.

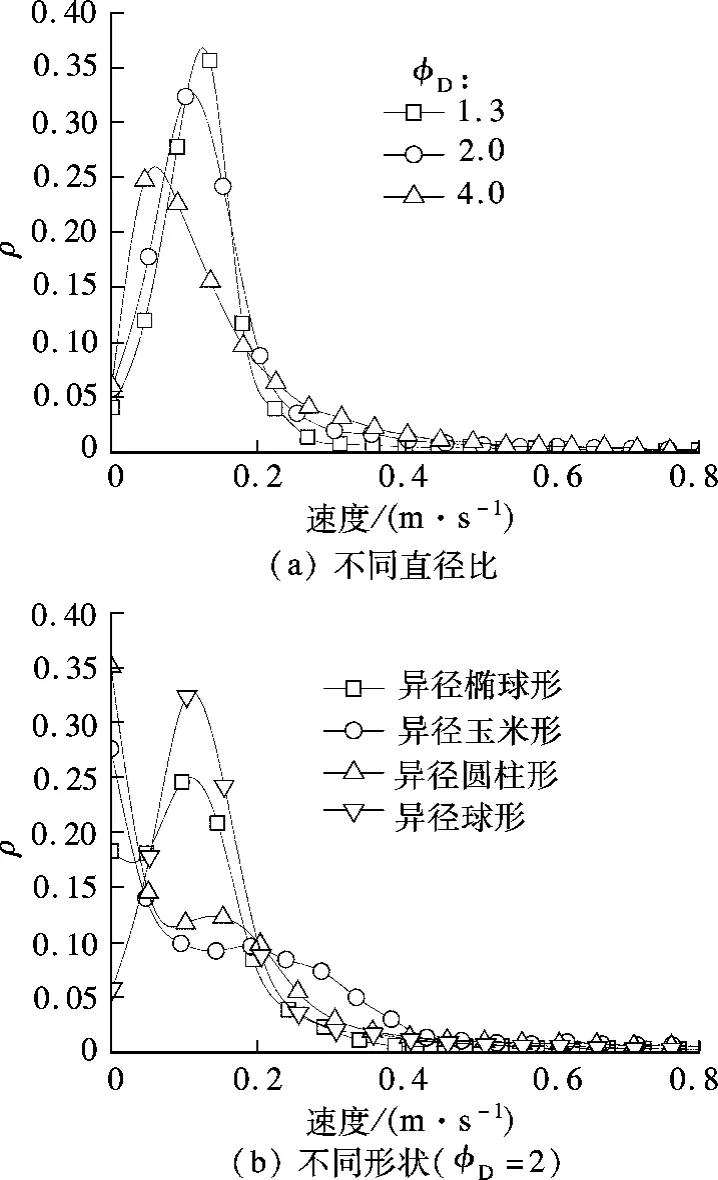
图6 异径混合颗粒的概率分布

当φD=2时，3种异径混合非球形颗粒和异径球形混合颗粒的概率分布情况见图6(b).由图可知，异径球形颗粒的概率分布只有一个峰，峰值为0.25，对应的速度值为0.1 m/s.异径椭球形混合颗粒的概率分布呈现2个峰，峰值分别为0.16和0.24，对应的速度值分别为0.001和0.1 m/s，第1个峰值对应于边壁处较小速度的颗粒，第2个峰值对应于中心处流动的颗粒.异径圆柱形混合颗粒和异径玉米形混合颗粒的概率分布相似，仅有1个峰，峰值分别为0.35和0.26，对应的速度均为0.001 m/s.

2.3 异径混合非球形颗粒的空隙率分布

空隙率是一个描述颗粒堆积结构的重要参数，它能影响床内压降、床层渗透性、气体速度分布等，与颗粒的物理特性、堆积状态以及颗粒的运动状态有关.

图7为异径混合颗粒的空隙率分布比较图.图中，ε表示空隙率，x表示颗粒与一侧壁面的距离.由图7(a)可知，异径混合颗粒的局部空隙率分布和均质颗粒的空隙率分布趋势基本相同，即在靠近壁面处，由于壁面作用，出现振幅减小的阻尼振荡，之后再进入稳定的波动阶段.不同的是，异径混合颗粒的壁面作用较小，在距壁面0.01 m处便进入稳定波动阶段.异径玉米形混合颗粒的空隙率波动范围为0.35～0.42，平均空隙率为0.4;异径球形混合颗粒的空隙率波动范围为0.37～0.45，平均空隙率为0.43;异径椭球形混合颗粒的空隙率波动范围为0.42～0.52，平均空隙率为0.47;异径圆柱形混合颗粒的空隙率波动范围为0.37～0.51，平均空隙率为0.453.由此可知，异径圆柱形混合颗粒的空隙率波动范围最大，平均空隙率也最大;其次为异径椭球形混合颗粒、异径球形混合颗粒;异径玉米形混合颗粒的空隙率波动范围最小，平均空隙率最小.由图7(b)可知，与均质颗粒相比，壁面对不同尺寸混合颗粒的空隙率影响范围较小，仅在距壁面0.012 m左右的范围内.此外，在不受壁面影响的区域内，二元混合物颗粒空隙率的波动较均质颗粒小，这与颗粒的堆积方式有关.混合物中颗粒直径比越大，空隙率越小.

图7 异径混合颗粒的空隙率分布比较

3 结语

本文对异径混合球形、非球形颗粒在移动床中的流动特性进行了数值模拟研究.提出了多元颗粒模型的思想，并通过实验验证了模型的可靠性.探讨了异径混合球形和非球形颗粒在移动床中流动时的流型、概率分布特性以及空隙率分布情况.结果表明:异径非球形颗粒由于颗粒形状的原因，滚动性比较差，流动开始便呈现出漏斗流的流型;异径球形颗粒则在流动的初始阶段呈现为整体流，经过一段时间后才慢慢向漏斗流转变.对于不同颗粒直径比的异径混合球形颗粒，颗粒直径比越小，概率密度峰值越大，速度分布范围越窄;反之，颗粒直径比越大，对应的概率密度峰值越小，速度分布范围越宽.在空隙率分布方面，颗粒直径比越大，平均空隙率越小;异径圆柱形混合颗粒的空隙率波动范围最大，平均空隙率也最大.

［1］ Anand A，Curtis J S，Wassgren C R，et al.Predicting discharge dynamics from a rectangular hopper using the discrete element method(DEM)［J］.Chemical Engineering Science，2008，63(24):5821-5830.

［2］ Chou C S，Hsu J Y.Kinematic model for granular flow in a two-dimensional flat-bottomed hopper［J］.Advanced Powder Technology，2003，14(3):313-331.

［3］ Zhang K F，Ooi J Y.A kinematic model for solids flow in flat-bottomed silos［J］.Geotechnique，1998，48(4):545-553.

［4］ Kohring G A，Melin S，Puhl H，et al.Computer simulations of critical，non-stationary granular flow through a hopper［J］.Computer Methods in Applied Mechanics and Engineering Journal，1995，124(3):273-281.

［5］ Li J T，Langston P A，Webb C，et al.Flow of spherodisc particles in rectangular hoppers:a DEM and experimental comparison in 3D［J］.Chemical Engineering Science，2004，59(24):5917-5929.

［6］ Grof Z，Kohout M，Stepanek F.Multi-scale simulation of needle-shaped particle breakage under uniaxial compaction［J］.Chemical Engineering Science，2007，62(5):1418-1429.

［7］ Cleary P W，Sawley M L.DEM modeling of industrial granular flows:3D case studies and the effect of particle shape on hopper discharge［J］.Applied Mathematical Modeling Journal，2002，26(2):89-111.

［8］ Matuttis H G，Luding S，Herrmann H J.Discrete element simulations of dense packings and heaps made of spherical and non-spherical particles［J］.Powder Technology，2000，109(1):278-292.

［9］ Favier J F，Fard A，Kremmer M，et al.Shape representation of ax-symmetrical，non-spherical particles in discrete element simulation using multi-element model particles［J］.Engineering Computations，1999，16(4):467-480.

［10］ Dziugys A，Peters B.An approach to simulate the motion of spherical and non-spherical fuel particles in combustion chambers［J］.Granular Matter，2001，3(4):231-266.

［11］ Chung Y C，Ooi J Y.A study of influence of gravity on bulk behavior of particulate solid［J］.Particuology，2008，6(6):467-474.

［12］ Zhong W Q，Zhang Y，Jin B S，et al.Discrete element method simulation of cylinder-shaped particle flow in a gal-solid fluidized bed［J］.Chemical Engineering＆Technology，2009，32(3):386-391.

［13］ Coetzee C T，Jels D N.Calibration of discrete element parameters and the modeling of silo discharge and bucket filling［J］.Computers and Electronics in Agriculture，2009，65(2):198-212.

［14］ Tao He，Jin Baosheng，Zhong Wenqi.Discrete element method modeling of non-spherical granular flow in rectangular hopper［J］.Chemical Engineering and Processing:Process Intensification，2010，49(2):151-158.

［15］ Johanson J R.Modeling flow of bulk solids［J］.Powder Technology，1972，5(2):93-99.

［16］ Wu J T，Binbo J，Chen J Z，et al.Multi-scale study of particle flow in silos［J］.Advanced Powder Technology，2009，20(1):62-73.

Numerical simulation of flow characteristics of non-spherical particle mixture with different diameters flowing in moving bed

Tao He1Zhong Wenqi2Jin Baosheng2Ren Bing2Yuan Zhulin2

(1Department of Civil and Architectural Engineering，Zhengzhou Institute of Aeronautical Industry Management，Zhengzhou 450000，China)
(2School of Energy and Environment，Southeast University，Nanjing 210096，China)

To study the the flow characteristics of non-spherical particles in the moving bed，a multielement particle model was developed to simulate the corn-shaped，ellipsoidal and cylinder particles flowing in the moving bed.The flow patterns，probability densities and voidage distributions of spherical and non-spherical particle mixture with different diameters in the moving bed were studied.The results show that the flow pattern of the spherical particle mixture with different diameters changes from mass flow to funnel flow gradually，while that of the non-spherical particle mixture with different diameters exhibits funnel flow from the very beginning.The probability density has only one peak value for spherical and non-spherical ones，but the corresponding velocity values are different.Both the fluctuation range and the mean voidage of the cylinder particle mixture with different diameters are the largest.For the non-spherical particle mixture with different diameters，the mean voidage becomes smaller with the increase of the diameter ratio.

multi-element particle model;non-spherical particle;moving bed;flow characteristic

TK16

A

1001－0505(2012)06-1122-05

10.3969/j.issn.1001 －0505.2012.06.019

2012-06-05.

陶贺(1982—)，女，博士，讲师;金保昇(联系人)，男，教授，博士生导师，bsjin@seu.edu.cn.

国家自然科学基金资助项目(50976025).

陶贺，钟文琪，金保昇，等.异径混合非球形颗粒在移动床中流动特性的数值模拟［J］.东南大学学报:自然科学版，2012，42(6):1122-1126.［doi:10.3969/j.issn.1001 －0505.2012.06.019］