模型参数摄动下的车辆侧向动力学混沌研究

黄 晨 陈 龙 袁朝春 江浩斌 陈月霞

(江苏大学汽车与交通工程学院，镇江 212013)

模型参数摄动下的车辆侧向动力学混沌研究

黄 晨 陈 龙 袁朝春 江浩斌 陈月霞

(江苏大学汽车与交通工程学院，镇江 212013)

以车辆多自由度模型为研究对象，耦合轮胎神经网络模型，依据某车型参数及某子午线轮胎在汽车轮胎道路旋转测试台上进行瞬态试验所测得的轮胎接地力数据，构建非线性侧向动力学系统.该系统结构复杂，不易得到解析解，因此借用数值计算方法来研究随着前轮转角和车速变化下的横摆角速度和侧偏角的时间序列内在特性.仿真结果表明，在固定参数下系统具有趋于不动点的稳态响应.当系统参数进行不同频率的周期性摄动时，由计算功率谱、分岔图和最大李雅普诺夫指数图给出了系统稳定和发生分岔的条件和过程及混沌吸引子的特点，为进一步进行混沌控制提供理论参考.

混沌;侧向动力学;非线性;神经网络

在高速公路上常常发生车辆的转向失控致使侧翻的车毁人亡安全事故.车辆的失稳主要与轮胎的侧向力有关，影响侧向力的主要因素是侧偏角［1］.当车辆高速转弯行驶时，侧偏角变化较小，轮胎的侧向力呈线性变化，而在较高的侧向加速度范围内，轮胎特性为非线性，侧向力非线性变化，转向效果减弱［2］.显然，车辆在复杂工况和不确定因素的影响下，行驶过程中的轮胎工况、垂直载荷、侧向力和切向力等都是变化的，需要建立更加精确的多因素的强非线性模型(如神经网络模型等)才能满足控制的要求［3］.

目前研究转向稳定性的主要方法为非线性动力学.如Shoji等［4］建立的侧偏角与侧偏角变化率相平面，对于定量确定侧向稳定区域提供了较好的方法，但不足在于忽略了转向盘转角、车速以及车身侧偏角对稳定区域的重要影响，并且受轮胎简化模型的限制，未从理论上分析在该稳定区域之外车辆的状态及变化趋势.郭孔辉［5］建立的转弯动能与前进动能之比相平面对于解释试验现象、进行定量分析都显示了很好的效果，但有一定的应用局限.

施树明等［6］构建了车辆系统关于车身侧偏角、转向盘转角以及车辆速度等主要参量的势能函数，并对势能函数进行定性和定量分析得到了车辆转向稳定区域.杨秀建［7］则借助于非线性动力学中心流形理论将高维系统降为一维中心流形系统，通过理论推导和实例分析，得出分岔极限环现象，并且指出随着车速和前轮转角的增加将发生鞍结分岔.

Liu等［8］研究了基于司机调节行为的前轮非线性转向模型，并分析了系统Hopf分岔，然后验证了前轮受周期扰动时，系统将出现混沌运动.Chang［9］则计算了线控转向汽车在一定参数变化范围内的分岔图，发现了系统的周期和混沌运动，并提出了汽车转向状态时的混沌反馈控制器.

从以上分析可看出大多数方法是建立在混沌系统精确数学模型基础上的，即需要精确知道驱动系统和响应系统的模型和参数.然而由于环境的变化、元器件的老化及建模误差等因素，系统参数的摄动是不可避免的.因此，研究系统参数摄动的问题具有重要的现实意义.然而耦合神经网络的微分方程系统，含有多个模型参数，如果这些参数摄动会使系统表现出复杂的非线性、非平稳特征［10］.

在非线性系统中，周期信号通过具有非线性特性的传输通道后，常常会转变为具有噪声特性的混沌信号，换言之，这些非线性系统会将原来的周期输入掩蔽，从而产生混沌噪声［11］.因此，为了能更好地研究系统的动力学特性，本文首先建立耦合RBF神经网络模型的整车模型系统，研究固定参数下初值扰动的系统时间序列内在特性，然后对系统参数进行不同频率的周期性激励，通过多种途径分析系统稳定和发生分岔的条件和过程.

1 理论模型

假定汽车前进方向速度不变，不考虑地面切向力对轮胎侧偏特性的影响和空气动力的作用等，建立基于转向工况的整车动力学模型，如图1所示.

1.1 整车模型

汽车转向过程中，车身侧倾角的变化对汽车侧偏角和横摆角速度的影响不可忽略.因此，考虑车身侧倾影响，建立整车转向运动方程.

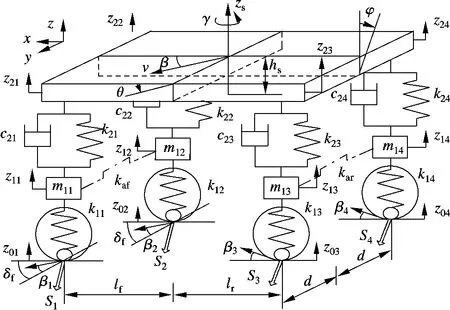
图1 整车动力学模型

整车侧向运动方程

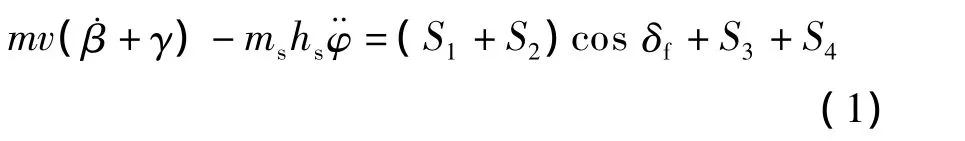
整车横摆运动方程

车身垂直运动方程

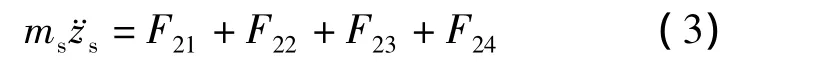
车身俯仰运动方程

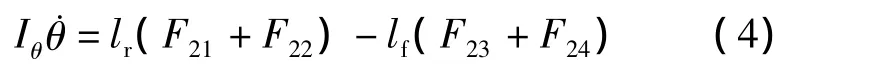
车身侧倾运动方程

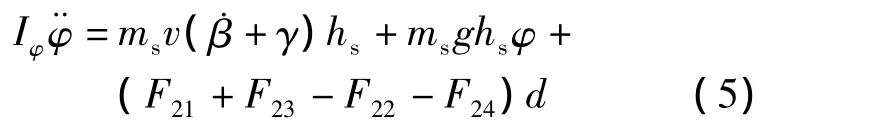
非悬挂质量垂直运动方程

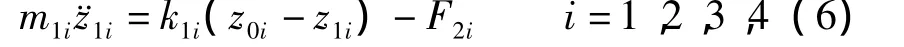
式中，m，ms为整车质量和悬挂质量;v为车速;β，˙β为质心侧偏角和质心侧偏角速度;hs为侧倾中心高度;φ，¨φ为车身侧倾角和车身侧倾角加速度;Si(i=1，2，3，4)为轮胎侧偏力;Iγ为整车横摆转动惯量;γ，˙γ为横摆角速度和横摆角加速度;lf，lr为前、后轮到质心距离;zs，¨zs为车身垂直位移和车身垂直加速度;F2i为悬架对车身的合力;Iθ，Iφ为车身俯仰转动惯量和车身侧倾转动惯量;θ，˙θ为车身俯仰角和车身俯仰角速度;d为1/2轮距;m1i为非悬挂质量;k1i为轮胎刚度;z0i为路面位移;z1i，˙z1i，¨z1i为非悬挂质量垂直位移、垂直速度和垂直加速度;z2i，˙z2i，¨z2i为悬挂质量垂直位移、垂直速度和垂直加速度;考虑横向稳定杆对车身侧倾角的影响，悬架作用合力为

式中，k2i为悬架刚度;c2i为悬架阻尼系数;kaf，kar分别为前、后悬架稳定杆角刚度.

当俯仰角θ、侧倾角φ在小范围内，近似有

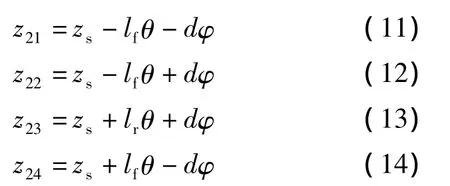
1.2 轮胎模型

实际车辆在非平坦路面上行驶，对轮胎施加的影响是时变的，因此需要建立动态模型适应环境的变化.采用下式所建的自适应神经网络(ANN)较为合适.

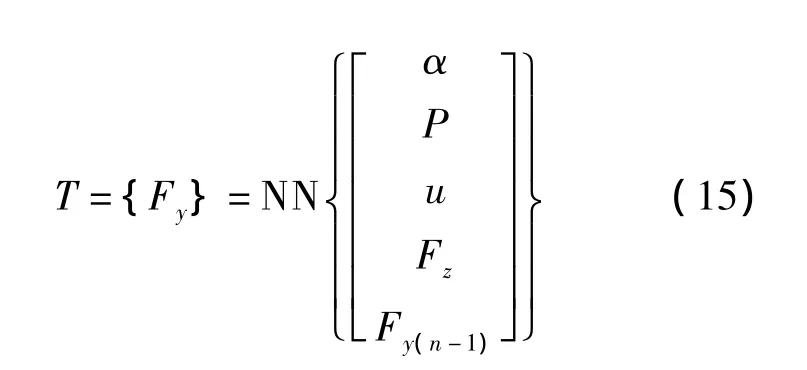
ANN包括输入层、隐含层和输出层.输入层包含5个变量，分别为侧偏角α、胎压P、垂直载荷Fz、车速u和前一步侧向力Fy(n－1).隐含层由若干层非线性传递函数组成.输出层由单个变量轮胎侧向力Fy构成.

本文将韩泰165/65R13子午线轮胎在江苏大学汽车轮胎道路旋转测试台上进行了瞬态试验，测得轮胎接地力数据，采用5-8-1的网络结构对试验数据进行拟合.从图2中可看出ANN模型较好地拟合了试验数据，而Magic Formula由于自身三角函数作为基函数的特点，拟合曲线只能接近试验数据，对侧向力的逼近有部分失真.

该网络隐含层神经元的输入为

式中，θj(k)为隐含层中第j个神经元的输入值;pi(k)为输入层输出;wij为输入层至隐含层的连接权重值.隐含层的输入和输出之间的联系采用Sigmoid函数关系，即隐含层神经元的输出表达为

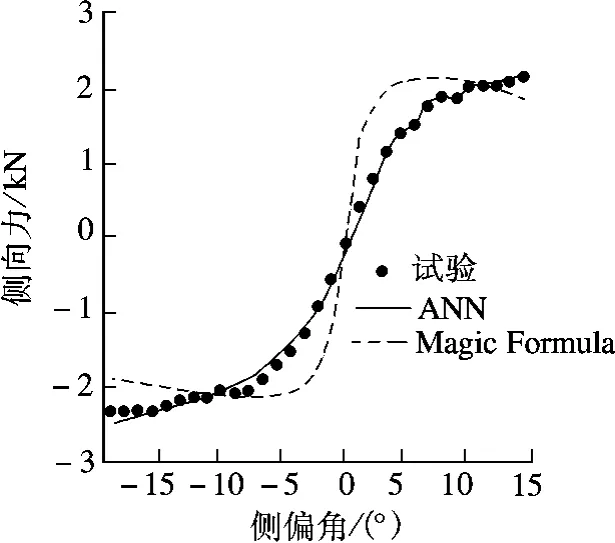
图2 ANN与Magic Formula模型比较

式中，ξj为隐含层第j个神经元的输出;f［ψ］=1/［1+exp(－ψ)］.输出层包含 1 个神经元，输出层神经元的输入函数为

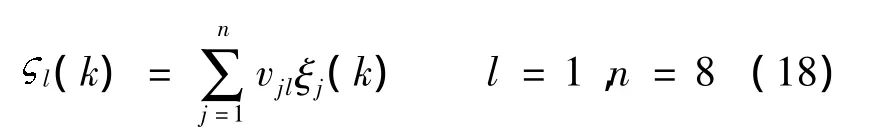
式中，vjl为隐含层至输出层的连接权重值.输出层的输出与输入的联系为Sigmoid函数关系，表示为

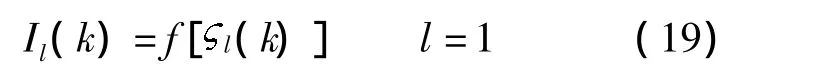
式中，Il为输出层神经元的输出.

假设左右侧车轮的侧偏角相等，则前后车轮侧偏角可表示为

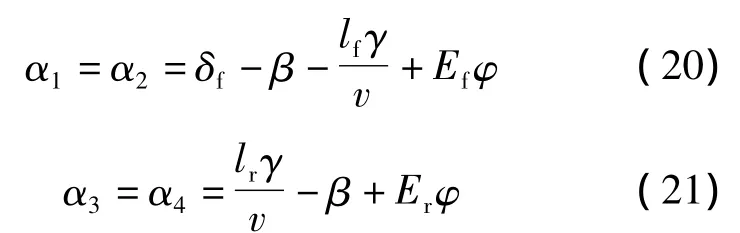
式中，α1，α2为前轴左右侧车轮的侧偏角;α3，α4为后轴左右侧车轮的侧偏角.

2 车辆侧向动力学混沌研究

2.1 仿真计算

对于耦合神经网络的非线性动力系统，解析解推导过程极其繁琐，实际应用较为困难.因此，需要借助数值方法来得到其近似解，即将微分方程转换为差分方程求解.本文基于Matlab/Simulink搭建仿真模型，计算流程如图3所示，模型参数参照某微型车设计参数，如表1所示.

判别混沌系统的方法主要有功率谱法、主分量分析法、庞加莱截面法、最大Lyapunov指数法和相平面法［12］.本文采用最大Lyapunov指数法和相平面法.

在计算最大Lyapunov指数过程中，采用时间序列重构，对每个点Vj寻找其最近邻点Vj'.

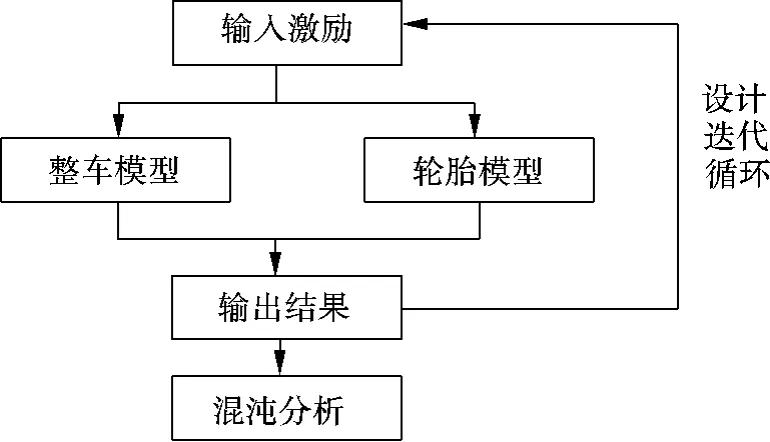
图3 计算流程图

表1 模型参数

定义分离间隔

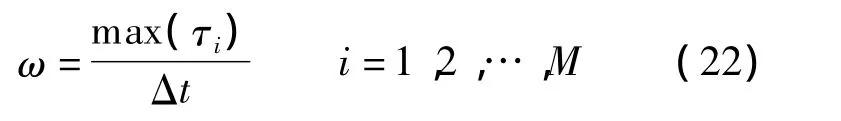
假定dj(0)为Vj到其最近邻点Vj'的距离，即

对相空间中的每个点Vj，计算出其最近邻点在第i步向前演化后的距离，即

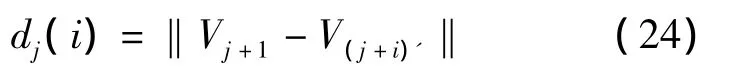
式中，i=J0，J0+1，…，N.

假定Vj的最近邻点以最大Lyapunov指数的速率发散，即dj(i)=dj(0)eλ(iΔt)，两边取对数，得lndj(i)=lndj(0)+ λ(iΔt).针对 lndj(i)相对iΔt的曲线，利用最小二乘法拟合得到最大Lyapunov指数λ1为

式中为非零的dj(i)个数.

2.2 结果分析

横摆角速度和侧偏角是车辆转向过程中驾驶者的乘坐和视觉感受评价指标.因此研究β和γ的动力学行为，对车辆转向中的各种现象的解释、操稳性的评价以及控制等问题都有重要意义.

本文首先在固定参数的情况下，以初值β0=0，γ0=0进行仿真计算，观察β和γ的时间历程(见图4).从图中可看出，从初值开始经过一段时间的振荡，最终稳定在不动点γ=0.875 rad/s，β=0.435 8 rad.

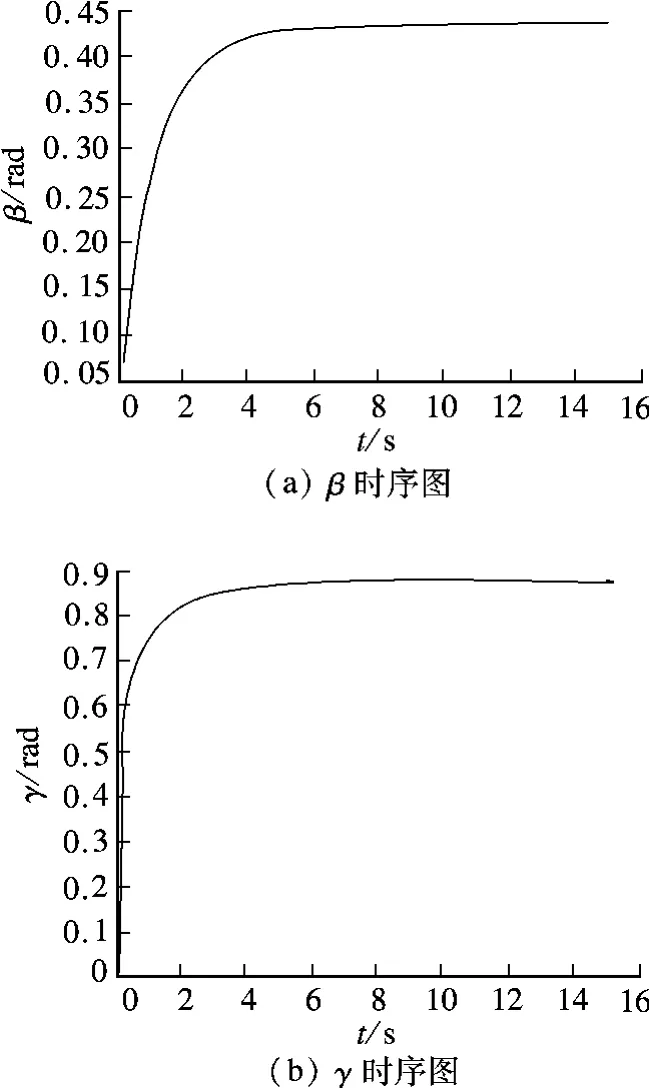
图4 固定参数下β和γ时序图

由于车辆在道路行驶过程中，外界环境的各种变化会对车辆状态产生影响，因此研究变参数的系统动力学行为更有实际运用价值，并且参数摄动系统往往表现出复杂的非线性、非平稳特征.非平稳意味着控制系统的某些参数或条件是随时间变化的，这类系统随时间的延长会表现出丰富多变的复杂动力学特性，所以具有较高的研究意义.

本文选取具有实际意义并且在现实中常常遇到的前轮转角和车速发生变化的情况进行讨论.分别对系统中的参数前轮转角和速度给予一个周期性的激励，观察β和γ映射的动力学行为.在相平面图中可以对以上结论加以佐证，在图5(a)中β和γ出现了环状混沌吸引子，并且在环状轨道中呈现无序状态.说明系统对前轮转角的参数摄动较为敏感，需要加以控制.而在图5(b)中β和γ变化轨迹为椭圆轨道，并且轨道呈规律性变化.

图5 参数摄动下β和γ相平面图

为了进一步分析系统稳定和发生分岔的条件和过程及混沌吸引子的特点，对出现混沌的前轮转角摄动进行深入分析.不同频率摄动下的γ功率谱分析可以将其频率成分展现出来，从而可以方便地区分单周期信号、多周期信号和非周期信号.从图6(a)、(b)中可看出，ω =1 rad/s时，在f=0.159 2 Hz处附近出现了逐渐降低的基频和谐频成分的离散谱特征，说明γ呈现简单的1周期性.而在ω=10 rad/s时，呈现孤立的f=1.592 Hz的共振特征，也符合1周期性的特点.

从功率谱图6(c)中可看出，频谱已不再是一个分立的离散谱，而是具有连续的线状谱特征.图中除了出现谐波和分谐波成分外，还出现了很多突变的频率成分，它们连在一起构成连续谱.从频谱分析的角度来看，在ω=100 rad/s时，γ振荡为非周期性运动特征，显示系统已出现混沌特性.

在分岔图7(a)中，当初始条件(圆频率ω)连续增加时，γ运动状态始终保持稳定的1周期.在ω达到15 rad/s时，γ运动状态突变成混沌状态.随着ω的进一步增加，ω在45 rad/s时γ运动状态又突变成4周期运动.在短暂的稳定后又进入混沌状态，最终随着ω的不断增加，收敛于1周期运动.

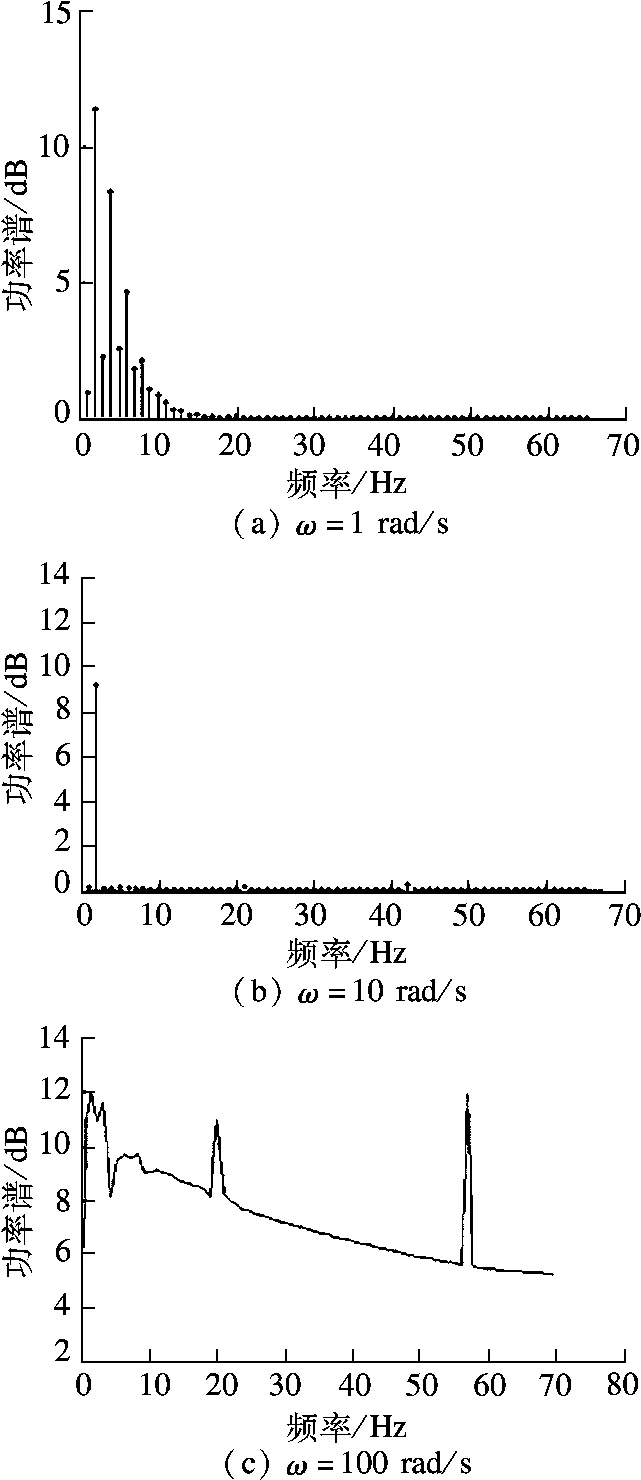
图6 不同圆频率的功率谱分析

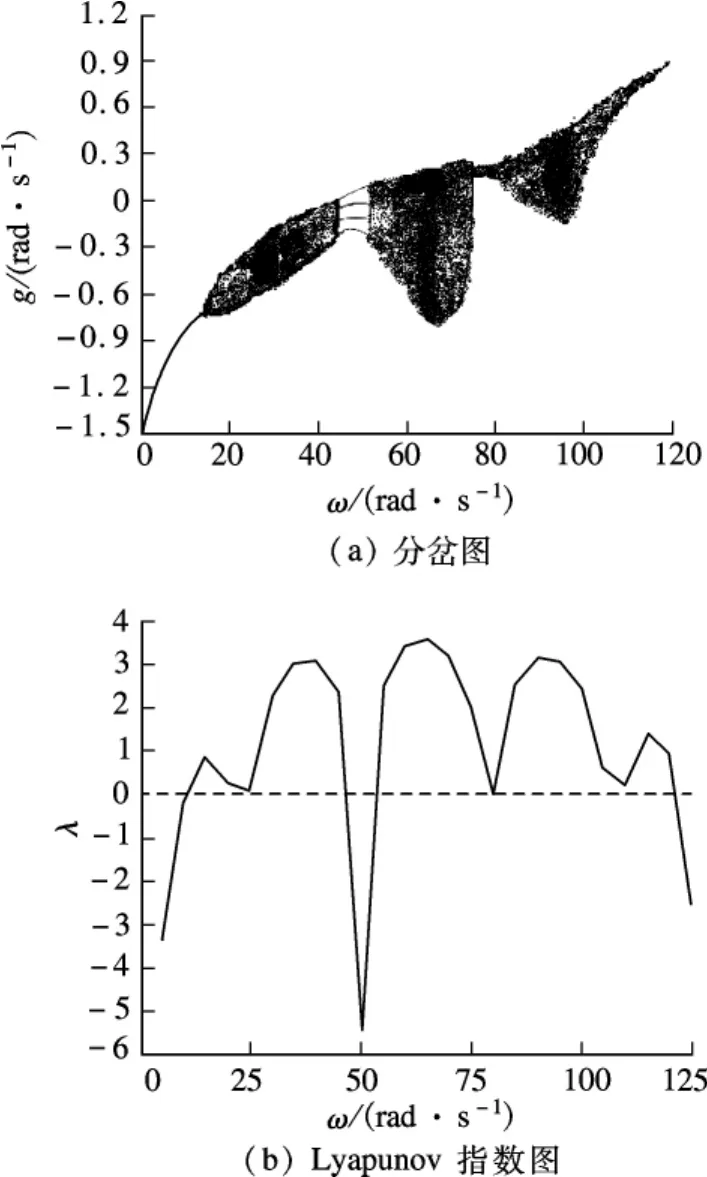
图7 混沌分析结果

从图7(b)中可看出，当ω从零开始时，λ从负值开始并且随着ω增大不断增大.当ω=15 rad/s时，λ=0.随后λ为正，表明系统出现了混沌状态.对应分岔图7(a)上γ运动状态从1周期进入混沌.在ω从15 rad/s到50 rad/s过程中，λ的变化是从零开始的增大减小交替进行的波动过程.在25 rad/s和40 rad/s处出现了λ局部最小值，对应分岔图7(a)上为吸引子的密集分布.在ω趋向50 rad/s的过程中λ急剧变化，出现全局最小值，分岔图上呈现吸引子由混沌变为4周期，维持短暂稳定过后又出现混沌状态，并在ω=65 rad/s处λ再次达到最大值并且是全局最大，对应分岔图上表现为一条密集狭长的带状混沌吸引子.随后λ逐渐下降，混沌吸引子的密集程度相应变稀、范围变窄，于ω=80 rad/s处达到最窄，λ趋近于零后再度增加.当ω达到95 rad/s时再次出现局部最大值，后呈下降趋势，期间有一个小的峰值才下降过零，趋向较大负值，对应分岔图上的混沌吸引子不断稀薄，收敛为稳定不动点.

3 结语

本文将神经网络轮胎和整车模型相结合，建立了一类耦合的微分方程组.通过对时间序列的研究，发现在固定参数下该系统对初值的扰动表现出很强的稳定性.而当系统参数进行不同角频率的周期性摄动时，通过计算功率谱、分岔图和最大李雅普诺夫指数图给出了系统稳定和发生分岔的条件和过程及混沌吸引子的特点.以上研究对轮胎模型参数周期性摄动下的车辆侧向非线性动力学行为研究及其混沌控制具有参考价值.

［1］Glaser H.Electronic stability program ESP［M］.Lycksele，Sweden:Audi Press，1996.

［2］彭旭东，孟祥恺，郭孔辉，等.冰面和干燥路面上轮胎侧偏特性的试验研究［J］.机械工程学报，2004，40(7):24-28.

Peng Xudong，Meng Xiangkai，Guo Konghui，et al.Experimental study of cornering properties of a tire on an ice and a dry pavement［J］.Chinese Journal of Mechanical Engineering，2004，40(7):24-28.(in Chinese)

［3］陈龙，黄晨，江浩斌.基于智能体-神经网络的轮胎侧偏特性［J］.机械工程学报，2012，48(2):153-158.

Chen Long，Huang Chen，Jiang Haobin.Cornering properties of pneumatic based on agent and neural network tire［J］.Journal of Mechanical Engineering，2012，48(2):153-158.(in Chinese)

［4］ Shoji I，Lkuo K，Masaki Y.Analysis on vehicle stability in critical cornering using phase plane method［J］.JSAE Review，1995，16(2):287-292.

［5］郭孔辉.汽车操纵动力学［M］.长春:吉林科学技术出版社，1991.

［6］施树明，毛振勇，向辉，等.车辆转向的稳定性非线性分析方法［J］.机械工程学报，2007，43(10):77-81.

Shi Shuming，Mao Zhenyong，Xiang Hui，et al.Nonlinear analysis methods of vehicle cornering stability［J］.Chinese Journal of Mechanical Engineering，2007，43(10):77-81.(in Chinese)

［7］杨秀建，王增才，彭伟利，等.极限工况下周期转向汽车侧向动力稳定性及分岔分析［J］.公路交通科技，2009，43(11):145-149.

Yang Xiujian，Wang Zengcai，Peng Weili，et al.Analysis on lateral dynamic stability and bifurcation of vehicle periodic steering under critical condition ［J］.Journal of Highway and Transportation Research and Development，2009，43(11):145-149.(in Chinese)

［8］Liu Z，Payre G，Bourassa P.Nonlinear oscillations and chaotic motions in a road vehicle system with driver steering control［J］.Nonlinear Dynamics，1996，9(3):281-304.

［9］ Chang S C.On controlling a chaotic vehicle dynamic system by using dither［J］.International Journal of Automotive Technology，2007，8(4):467-476.

［10］吴光强，盛云.混沌理论在汽车非线性系统中的应用进展［J］.机械工程学报，2010，46(10):81-87.

Wu Guangqiang，Sheng Yun.Review on the application of chaos theory in automobile nonlinear system［J］.Chinese Journal of Mechanical Engineering，2010，46(10):81-87.(in Chinese)

［11］张东翔，薛荣书，谭世语.周期性机械激励液液体系相界面层的传质特性［J］.化工学报，2000，51(1):108-114.

Zhang Dongxiang，Xue Rongshu，Tan Shiyu.Mass transfer characteristics of interfacial layer mechanically activated in liquid-liquid system ［J］.Journal of Chemical Industry and Engineering，2000，51(1):108-114.(in Chinese)

［12］余洋，米增强，刘兴杰.双馈风力发电机混沌运动分析及滑模控制混沌同步［J］.物理学报，2011，65(7):158-167.

Yu Yang，Mi Zengqiang，Liu Xingjie.Analysis of chaos in doubly fed induction generator and sliding mode control of chaos synchronization［J］.Acta Physica Sinica，2011，65(7):158-167.(in Chinese)

Chaos study of vehicle lateral dynamics based on perturbation parameter

Huang Chen Chen Long Yuan Chaochun Jiang Haobin Chen Yuexia

(School of Automobile and Traffic Engineering，Jiangsu University，Zhenjiang 212013，China)

A vehicle model with multiple degrees of freedom is regarded as object of study，which is coupled with tire neural network model.The nonlinear lateral dynamics system is established based on vehicle parameters and the tire data obtained from the transient test on the road rotation test bench.This system has a complicated structure，so it is difficult to obtain the analytical solution.The numerical method can be used to study the intrinsic properties of time sequence of yaw angular velocity and lateral declination with the changes in front wheel angle and the vehicle speed.The simulation results show that this system has a steady-state response tending to the fixed point when the parameters are fixed.Moreover，when system parameters make periodic perturbation with different frequencies，the calculation of power spectrum，bifurcation diagram and largest Lyapunov exponent diagram may provide the conditions and process to keep the system's stability and bifurcation.Meantime，the characteristics of chaotic attractor are analyzed，in order to provide a theoretical reference for the chaos control.

chaos;lateral dynamics;nonlinear;neural network

U463.341

A

1001－0505(2012)06-1111-06

10.3969/j.issn.1001 －0505.2012.06.017

2012-05-30.

黄晨(1984—)，男，博士生;陈龙(联系人)，男，教授，博士生导师，chenlong@163.com.

黄晨，陈龙，袁朝春，等.模型参数摄动下的车辆侧向动力学混沌研究［J］.东南大学学报:自然科学版，2012，42(6):1111-1116.［doi:10.3969/j.issn.1001 －0505.2012.06.017］