基于有效年龄的风力机多部件维修优化

苏 春 周小荃

(东南大学机械工程学院，南京 211189)

基于有效年龄的风力机多部件维修优化

苏 春 周小荃

(东南大学机械工程学院，南京 211189)

以风力机为对象，研究多部件系统的维修决策与优化问题，提出基于有效年龄的多部件维修优化模型.采用等周期检测方式，采取“继续工作”、“预防性维修”和“更换”3种维修策略，分析在各检测点处部件有效年龄的变化规律.考虑风力机部件之间的经济相关性，构造涵盖维修成本、更换成本、停机损失成本以及固定维护成本的维护成本函数，建立风力机维修成本优化数学模型;采用分支定界算法求解检测点处系统的最优维修策略.以风力机系统5个核心部件为对象，完成案例研究.结果表明:该模型能够有效描述风力机的维修过程，实现维护成本优化.

多部件维修;风力机;有效年龄;优化

能源是人类生存和发展的重要物质基础［1］.风能具有储量丰富、可再生和污染小等优点.近年来，风力发电在全球范围内受到关注［2］.风力机(wind turbine)是风电系统的核心装置，由叶片、齿轮箱、轴承、发电机等部件组成.受工作环境恶劣、驱动载荷不稳定、功能结构复杂等因素影响，风力机成为风电系统可靠性的薄弱环节［3］.

文献［4］将风力机视为具有多故障模式和多退化状态的系统，并考虑天气等因素，研究风力机齿轮箱的维修决策问题.文献［5］提出3种视情维修策略，研究不同参数条件下风力机叶片的最优维修策略.文献［6］采用半马尔科夫决策过程模型，实现风力机齿轮箱的维修优化.现有的研究主要关注齿轮箱、叶片等部件，很少从系统角度考虑由多个部件组成的风力机维修优化问题［7］.多部件系统维修决策需要考虑部件间的经济、结构及随机相关性.文献［8］综述了多部件系统维修研究现状，分析多部件系统维修的难点与趋势.文献［9］建立了串联多部件系统预防性维修模型，并采用动态规划方法求解模型.文献［10］的研究表明，考虑部件间的经济相关性能有效降低系统维修成本.目前，多部件系统维修优化主要包括2类模型:以系统可用度作为约束条件，寻求维修成本的最小化;以维修成本作为约束条件，实现系统可用度的最大化.对风力机多部件维修而言，上述2种优化模型考虑的因素较为简单，不能有效地定义风力机停机损失等特征.

本文以多部件组成的风力机为对象，引入有效年龄(effective age)，采用等周期检测方式，研究每个检测点上系统的维修策略，考虑系统维护成本，建立风力机多部件维修模型;采用分支定界算法求解模型，并通过算例验证模型和算法的有效性.

1 风力机多部件维修优化模型

从可靠性和维修性角度，可以将风力机视为由N个部件构成的可修复串联系统.采用等周期检测方式，根据部件和系统状态分别采用“继续工作”、“预防性维修”以及“更换”等维修策略，寻求风力机维护成本的最小化.

1.1 系统维修策略

有效年龄能够反映不同维修策略对系统的影响.设Xi，j为风力机第i个部件在第j个检测周期开始时的有效年龄为第i个部件在第j个周期结束时的有效年龄，T0为维修决策总时间，T为检测周期，则总检测周期为K=T0/T.显然有.在每个检测周期结束时检测系统，根据部件状态选择合适的维修策略.风力机部件的故障率随有效年龄增大而增大.当有效年龄较小时，部件发生故障的可能性较小，采用继续工作的策略;当有效年龄较大时，发生故障的可能性增大，需根据实际情况选择预防性维修或更换策略，以降低系统的有效年龄.采用上述3种维修策略，系统有效年龄的变化规律如下:

1)继续工作.若第i个部件在第j个检测点选择继续工作，则有

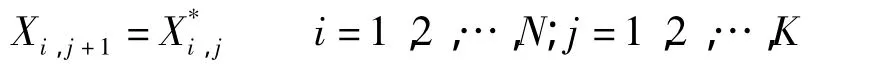
2)更换.若第i个部件在第j个检测点采用更换策略，忽略更换时间，则有

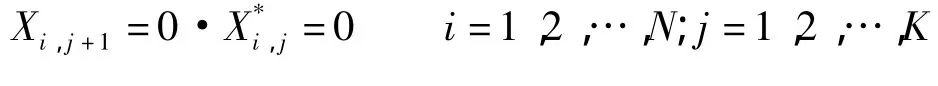
3)预防性维修.通过预防性维修降低部件发生故障的概率、减小部件的有效年龄.若第i个部件在第j个检测点进行预防性维修，忽略预防性维修时间，则有

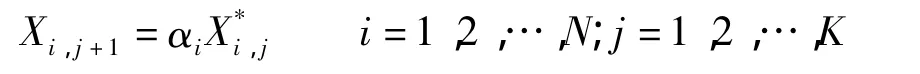
式中，αi为第i个部件的改善因子，用于定义预防性维修对系统有效年龄的改善效果，0＜αi＜1.当αi=1时，效果等同于继续工作;当αi=0时，效果等同于更换.

1.2 风力机维护成本构成

风力机维护成本主要包括预防性维修成本、更换成本、突发故障维修成本、停机损失成本以及固定维护成本等.

1)预防性维修成本

mi，j表示风力机第i个部件在第j个检测点的预防性维修决策变量.当mi，j=1时，第i个部件在第j个检测点进行预防性维修;当mi，j=0时，不进行预防性维修.若第i个部件预防性维修成本为Mi，则其在第j个检测点的预防性维修成本为Mimi，j.

2)更换成本

ri，j表示风力机第i个部件在第j个检测点更换的决策变量.当ri，j=1时，第i个部件在第j个检测点进行更换;当ri，j=0时，不进行更换.若第i个部件更换成本为Ri，则其在第j个检测点的更换成本为Riri，j.

3)突发故障维修成本

风力机运行过程中部件会发生突发性故障.考虑到风电场地处偏远、维修不便，部件故障后需等到下一个检测点才进行维修，并且在检测点处采用最小维修使部件恢复工作，不改变部件有效年龄.长期的观测数据表明，风力机部件故障的发生符合两参数威布尔分布［11］，因此风力机第i个部件在第j个周期内发生故障的概率为，式中 η，β 分别为两参数威布尔分布的尺度参数和形状参数.设部件i的最小维修成本为Fi，则部件i在第j个周期突发故障维修成本为.通常，最小维修成本小于预防性维修成本且预防性维修成本小于更换成本，即Fi＜Mi＜Ri(i=1，2，…，N).

4)停机损失成本

风力机是由多部件组成的串联系统，其中任一部件发生突发故障且无法及时维修时，风力机将进入停机状态，直到下一个检测点进行维修.风力机在第j个周期内的可靠度为，则系统在第j个周期的停机损失成本为其中cD为风力机的单位时间停机损失.

5)固定维护成本

设每次维护中因人力、设备投入产生的固定维护成本为Z.

1.3 维修优化模型

风力机维修决策的目标是在一定时间内使系统的总维护成本最小:

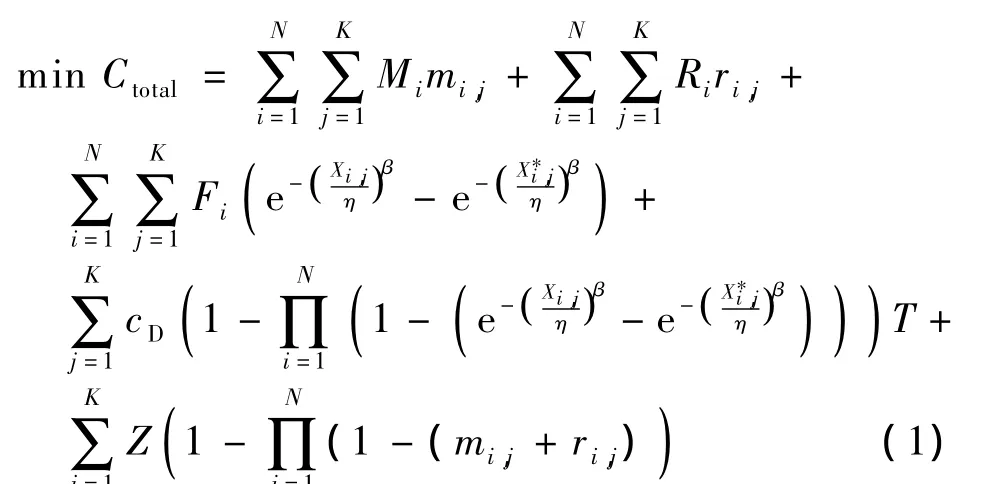
式中，Ctotal为由N个部件组成的风力机在第K个检测周期内的总维护成本，包括预防性维修成本、更换成本、突发故障维修成本、停机损失成本以及固定维护成本.

风力机维修决策需要考虑以下约束条件:

式(2)表示初始时刻时各部件的有效年龄为0.式(3)表示采用不同的维修策略时有效年龄的变化规律:若继续工作，则若进行预防性维修，则;若进行更换，则表示在检测点处，维修决策前有效年龄的变化规律.式(5)表示决策变量为0-1整数变量.式(6)表示在每个检测点只采用一种维修策略.式(7)表示有效年龄不小于0.

2 模型求解

上述优化模型属于非线性混合整数规划问题，可采用分支定界算法求解［12］，求解步骤如下:

①原优化模型记作A，除去模型中的整数要求，得到与原模型对应的松弛模型，记为模型B.求出模型B的最优解，若最优解符合模型A的整数条件，则计算停止，所得解即为原优化模型A的最优解;若解不符合整数条件，则将所对应的目标函数值记为C0total，并进行步骤②.

②用观察法寻找模型A的一个整数解，本文取mi，j=0，ri，j=0(i=1，2，…，N;j=1，2，…，K)进行试探，求得目标函数值，记为Ctotal.设C*total为模型A的最优目标函数值，则应有

③在模型B的最优解中任意选取一个不符合整数条件的变量进行分支，以mi，j为例，设mi，j=bi，j，以［bi，j］表示不超过bi，j的最大整数，构造 2个约束条件:mi，j≤［bi，j］，mi，j≥［bi，j］+1.分别将2个约束条件加入模型B中，得到2个后继子问题，不考虑整数条件求解2个后继子问题.

④将每一个后继子问题作为一个分支进行求解，并将结果与其他后继子问题求解结果进行比较，找出目标函数值最小者作为新的下界;从符合整数条件的分支中选择目标函数值最小者作为新的上界Ctotal;若不符合整数条件，上界值不变.

⑤若分支中有目标函数值大于Ctotal的，则不再考虑该分支;若目标函数小于Ctotal，且不符合整数条件，则重复步骤④，直至Ctotal=C0total，得到原模型A的最优整数解.

本文采用LINGO软件的分支定界算法模块，编制风力机维修优化模型的求解程序.

3 算例分析

某风力机主轴、轴承、齿轮箱、叶片、发电机等5种核心部件(简称部件1～部件5)的可靠性及维修性参数如表1所示［11］.

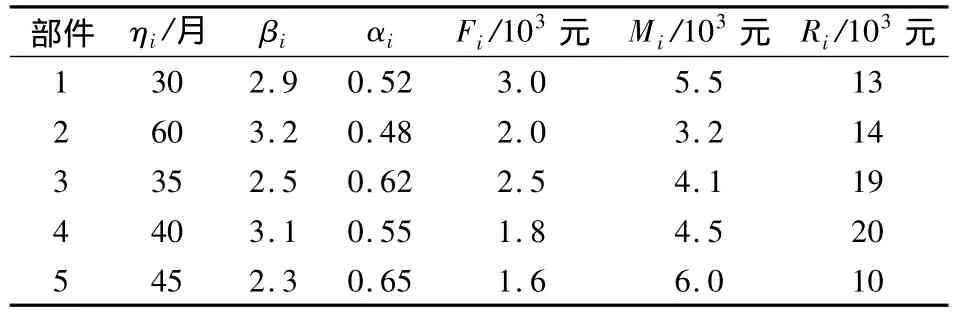
表1 风力机各部件参数设置

设检测周期为1个月，研究风力机在3年内的最优维修策略.设风力机的维修固定成本Z为4 000元，单位时间停机损失cD为12万元/月.采用分支定界法求解优化模型，得到3年内最优维护成本为21.7万元，各部件最优维修策略如表2所示.各部件有效年龄变化如图1所示.

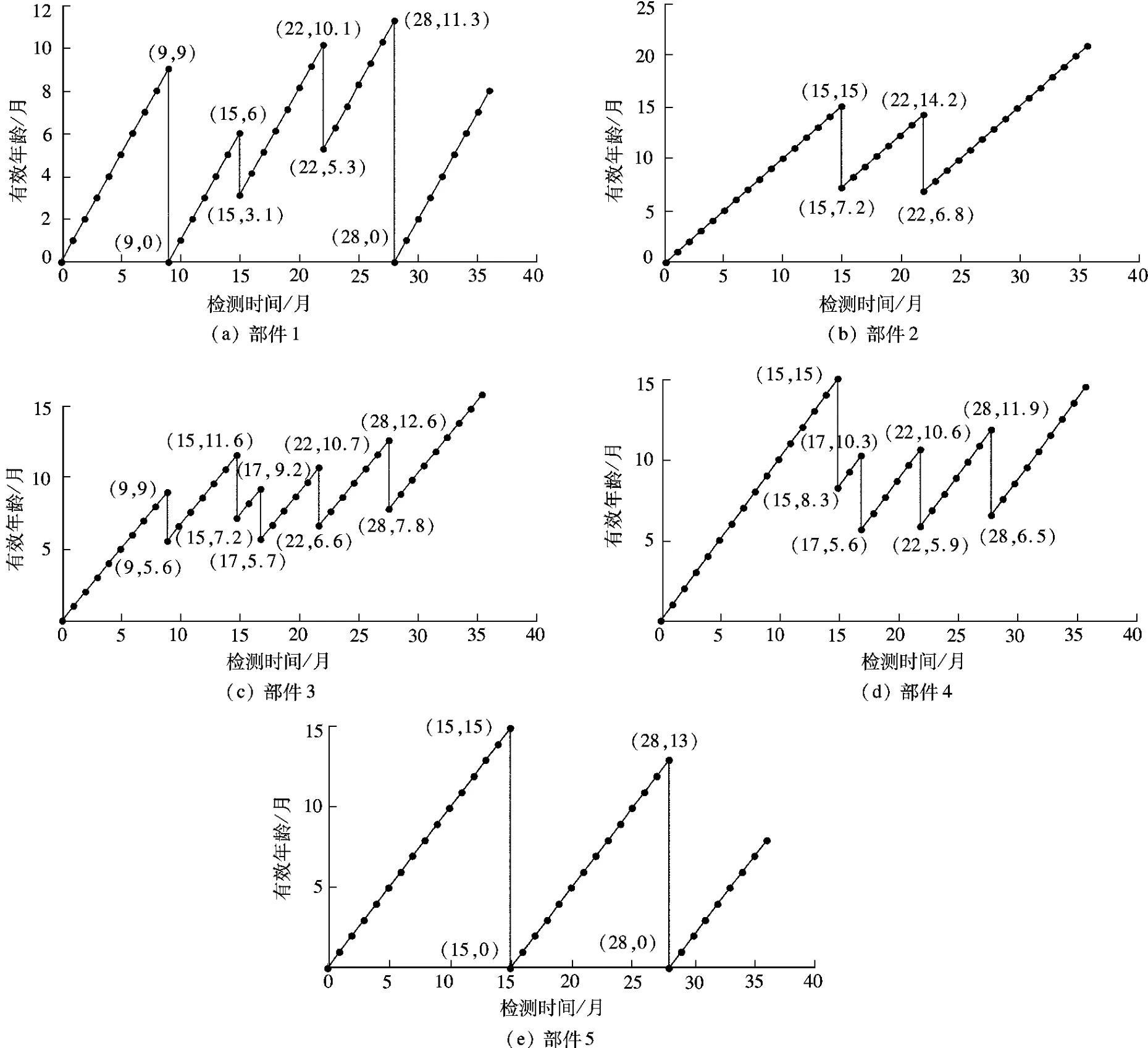
图1 各部件的有效年龄变化规律

由表2和图1可知:部件有效年龄由维修策略及改善因子共同决定.以部件1为例(见图1(a))，其在前8个检测周期没有采取任何维修措施，有效年龄呈线性增长趋势;第9个检测点处进行更换操作，有效年龄由9个月降为0;在第15个检测点进行预防性维修，有效年龄由从6个月降为3.1个月;随后部件1在第22个与第28个检测点处分别进行预防性维修与更换，有效年龄也随之变化.

研究结果表明:风力机的维修策略取决于各部件的预防性维修成本、更换成本及其可靠性特性等因素.例如:部件5在3年内有2次更换操作，没有预防性维修;部件2有多次预防性维修而没有更换操作.原因是相对于部件2，部件5的更换成本更低，预防性维修成本更高;且部件5故障概率较高，可能造成更大的停机损失.

若不考虑固定维护成本，在相同条件下风力机各部件最优维修策略如表3所示.

表3 不考虑固定维护成本时风力机各部件最优维修策略

比较表2及表3可知:①不考虑固定维护成本，各部件维修或更换活动将增多.以部件1为例，考虑固定维护成本时，部件1在3年内有4次预防性维修或更换，而不考虑固定维护成本，维修或更换活动增加到6次.②不考虑固定维护成本，部件的维修或更换活动趋于分散，而考虑固定维护成本时，部件的维修或更换活动相对集中.此外，考虑固定维护成本，3年内风力机最优维护成本为21.7万元;而不考虑固定维护成本，3年内风力机最优维护成本为19.6万元.显然，固定维护成本直接影响维修策略的制定与最优维护成本的大小.

4 结语

风力机是典型的多部件系统，结构复杂和工作环境恶劣使得此类系统的维修面临挑战.本文中建立了基于有效年龄的风力机多部件维修优化模型，考虑部件间经济相关性，分析多种维修策略，构建系统维护成本函数，并采用分支定界算法求解模型.该维修决策模型能有效描述由多部件组成的风力机系统维修优化问题，为风电场运营维护提供了理论依据，对其他多部件系统的维修决策也具有参考价值.

［1］江泽民.对中国能源问题的思考［J］.上海交通大学学报，2008，42(3):345-359.Jiang Zemin.Reflections on energy issues in China［J］.Journal of Shanghai Jiaotong University，2008，42(3):345-359.(in Chinese)

［2］ Liao Cuiping，Jochem E，Zhang Yi，et al.Wind power development and policies in China［J］.Renewable Energy，2010，35(9):1879-1886.

［3］ Herbert G M J，Iniyan S，Sreevalsan E，et al.A review of wind energy technologies［J］.Renewable and Sustain-able Energy Reviews，2007，11(6):1117-1145.

［4］ Byon E，Yu Ding.Season-dependent condition-based maintenance for a wind turbine using a partially observed Markov decision process［J］.IEEE Transactions on Power Systems，2010，25(4):1823-1834.

［5］ Besnard F，Bertling F.An approach for condition-based maintenance optimization applied to wind turbine blades［J］.IEEE Transactions on Sustainable Energy，2010，1(2):77-83.

［6］苏春，周小荃.基于半马尔科夫决策过程的风力机状态维修优化［J］.机械工程学报，2012，48(2):44-49.Su Chun，Zhou Xiaoquan.Condition-based maintenance optimization for wind turbines based on semi-Markov decision process［J］.Chinese Journal of Mechanical Engineering，2012，48(2):44-49.(in Chinese)

［7］ Tian Zhigang，Liao Haitao.Condition based maintenance optimization for multi-component systems using proportional hazards model［J］.Reliability Engineering and System Safety，2011，96(5):581-589.

［8］ Kobbacy K A H，Murthy D N P.Complex system maintenance handbook［M］.New York:Springer，2008.

［9］ Zhou Xiaojun，Xi Lifeng，Lee J.Opportunistic preventive maintenance scheduling for a multi-unit series system based dynamic programming［J］.International Journal of Production Economics，2009，118(2):361-366.

［10］ Moghaddam K S，Usher J S.Preventive maintenance and replacement scheduling for repairable and maintainable systems using dynamic programming［J］.Computers and Industrial Engineering，2011，60(4):654-665.

［11］ Andrawus J A，Watson J，Kishk M，et al.The selection of a suitable maintenance strategy for wind turbines［J］.Wind Engineering，2006，30(6):471-486.

［12］ Lust T，Roux O，Riane F.Exact and heuristic methods for the selective maintenance problem ［J］.European Journal of Operational Research，2009，197(3):1166-1177.

Maintenance optimization for multi-component of wind turbine based on effective age

Su Chun Zhou Xiaoquan
(School of Mechanical Engineering，Southeast University，Nanjing 211189，China)

Targeted at wind turbines，the maintenance decision and its optimization for a multi-component system is studied，and the corresponding maintenance optimization model is proposed based on effective age.The components'effective ages at each inspection point changing with maintenance policies including“continuing to work”，“preventive maintenance”，and“replacement”are analyzed by the periodical inspection method.By considering economic dependence among the components of wind turbine，the mathematical model of maintenance optimization is established.In the maintenance cost function，the repair cost，replacement cost，breakdown loss and fixed maintenance cost are included.The branch and bound algorithm is used to solve the model，and optimal policies at each inspection point are obtained for the system.A case study of a five-component wind turbine is provided.The result shows that the presented model can effectively describe the maintenance process of a wind turbine，and the maintenance cost can be optimized.

multi-component maintenance;wind turbine;effective age;optimization

TK83

A

1001－0505(2012)06-1100-05

10.3969/j.issn.1001 －0505.2012.06.015

2012-03-13.

苏春(1970—)，男，博士，副教授，博士生导师，suchun@seu.edu.cn.

苏春，周小荃.基于有效年龄的风力机多部件维修优化［J］.东南大学学报:自然科学版，2012，42(6):1100-1104.［doi:10.3969/j.issn.1001 －0505.2012.06.015］