竖向地震作用下桥梁结构的瞬态波响应分析

徐 然，尹晓春

(1.南京理工大学 力学与工程科学系，南京 210094;2.常州大学机械学院力学系，常州 213016)

近年来浅源近断层地震动的观测记录显示，竖向地震动与水平地震动分量的比值往往大于我国工程抗震设计规范中通常采用的2/3，而且出现了大幅值的竖向地震动加速度［1－3］。1994年发生在美国的 Northbridge地震，竖向加速度峰值高达1.18 g，是水平加速度峰值的1.79倍［1］，如此高的竖向地震动引起了极大的关注，因此成为竖向地震动研究的分水岭。在1995年的Kobe地震中，观测到的地面竖向加速度峰值高达水平值的两倍［2］。2008年发生在我国的汶川地震中，竖向地震动加速度峰值达到1g［3］，接近于水平加速度峰值。调查工程结构在竖向地震作用下的损坏发现，竖向地震动可能造成与水平地震动不同的损坏现象，如出现楼层整体压溃、墙体竖向夹角小于横向夹角的“X”型裂缝、受拉破坏的水平环缝、钢筋“灯笼状”压曲等特殊现象［1，4］。因此，被低估的竖向地震动对工程结构可能造成的损害，受到了越来越多的关注。

有关的研究显示，竖向地震动循环往复的地震力可能在桥梁的混凝土桥墩中产生巨大的应力，甚至丧失竖向承载能力，引起桥梁倒塌［5－6］。另一方面，支座与桥跨结构之间的接触力可能因竖向地震的作用而减小［7］，造成桥梁和桥墩之间的摩擦力减弱，使得落桥等震害更容易发生。竖向地震动产生的向上的拉力作用于支座上时，可引起桥梁与支座连接构件的拉断或者支座断裂等，也可能引起支座和上部结构发生暂时的分离，引发上跳现象［8］。Tanimura 等［9］假设桥跨发生了跳起后的再次落下撞击，采用动力学有限元方法模拟了下部结构的损坏情况，模拟结果与实际发生的损坏情况基本一致。

对于桥梁在水平地震分量激励下的地震响应时程分析，目前一般采用的研究方法有两种:其一是将桥梁简化为“梁－杆”模型，对耦合地震力(位移)的控制方程应用差分法求其数值解;其二是建立桥梁的有限元模型进行计算［10－13］。这两种计算方法均没有考虑结构的波动效应。针对竖向地震分量激励下的桥梁地震响应，需要将桥跨结构按梁结构，桥墩按杆结构考虑，从而建立“梁－杆”连续体模型。可以采用瞬态波特征法进行理论求解和分析，以得到竖向地震波传播过程中的桥梁响应。

本文应用弹性动力学理论中的瞬态波特征函数法，研究双跨连续梁桥在竖向地震动激励下的瞬态波传播问题。通过选取不同的竖向地震动与水平地震动的比值，对比研究桥墩和桥跨结构响应的变化。计算结果表明，该方法可以描述出地震激励产生的瞬态波的反射、相互作用和波碰撞等波传播现象，合理模拟竖向地震作用下的桥梁的动力学行为，求解复杂的地震激励下的结构瞬态波响应问题。

1 结构模型

本节针对一双跨连续梁桥(图1)阐述研究方法，研究该桥梁在竖向地震激励作用下的瞬态动力学响应。设桥跨结构参数为:跨长x0=50 m，横截面面积A=11.3 m2，截面惯性矩 I=22.7 m4;材料为 C50 混凝土:弹性模量 E=34.5 GPa，密度 ρ=2 500 kg/m3;桥墩结构参数为:墩高L=20 m，横截面面积Ar=15 m2;钢筋混凝土桥墩采用C20标号的混凝土:弹性模量Ec=30 GPa，密度ρc=2 500 kg/m3。桥墩纵向配筋为II级钢筋，直径40 mm，基本间距为100 mm，保护层厚度为50 mm，沿截面四周均匀布置，配筋率为1.3%。箍筋同样为II级钢筋，直径16 mm。钢筋的抗拉(压)设计强度fy=300 MPa，弹性模量为Ey=200 GPa。

由于桥墩中的混凝土和纵筋的弹性模量不一致，根据桥墩截面变形一致性假设，可以计算出桥墩的等效弹性模量Er=(EcAc+EyAy)/(Ac+Ay)，桥墩的等效应力σr为轴力除以桥墩横截面面积，其中Ac为截面混凝土面积，Ay为全部纵向钢筋的截面面积。

桥跨结构与桥墩之间的支座采用型号为XQZ6000的球型支座，该钢支座的弹性模量Ez=206 GPa，密度ρz=7 850 kg/m3，横截面面积 Az=0.51 ×0.51 m2，高度H=135 mm，在竖直方向y上没有位移约束。根据图1模型，可以计算出XQZ6000的球型支座承受的静接触力F0=17.27 MN，在该静载作用下，在球型支座各结构件压实的条件下，可以近似按照均质弹性体计算出支座的静变形量Δδ为:

它是桥墩静载变形量ΔL:

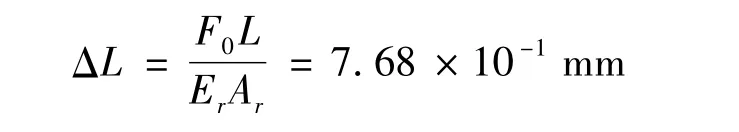
的4.43%。另外，弹性应力波在桥墩中传播时间tr为:

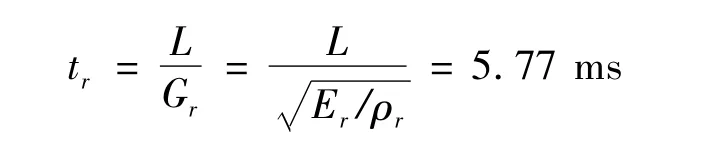
远远大于穿过支座需要的时间tz:

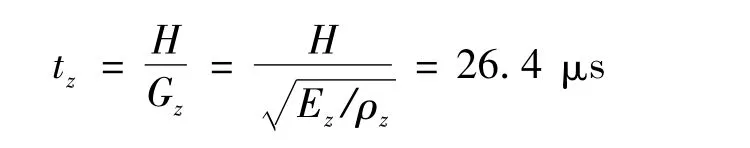
上述比较表明，支座的变形和波传播效应对于该双跨连续梁桥竖向地震响应的影响可以忽略。因此，在图1的模型中，不考虑支座的作用。

将竖向地震激励简化为简谐运动，以地震主要周期作为激励周期T，选取地震持续时间为10 s。对于复杂的竖向地震波动响应，可以通过FFT方法将其分解为各级简谐地震激励，然后利用简谐竖向地震激励的研究结果，采用叠加法加以分析。

对于图1所示的连续梁桥模型，不考虑支座的作用，将桥跨结构简化为梁Ω1，桥墩简化为杆Ω2，梁两端界面为ΓA和ΓB，梁和杆的接触界面为ΓC，杆下端的固支界面为ΓD。将梁的自重作为均布外载q施加在梁上，竖向地震激励的作用等效为基础运动B(t)，并取竖向地震波到达的时刻为计算的零时刻。

图1 双跨连续梁桥模型Fig.1 Model of two-span continuous bridge

2 瞬态波响应理论解

2.1 波动方程

桥跨结构采用Bernoulli-Euler梁模型，桥墩采用St.Venant杆模型。应用弹性动力学理论，得到梁Ω1和杆Ω2的波动方程为:

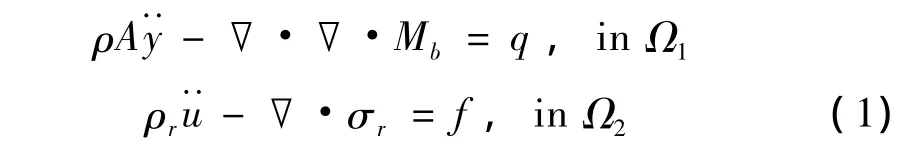
其中，y和u分别为梁的挠度和杆的轴向位移，Mb为梁的弯矩，σr为杆的轴向应力，不计桥墩体力时f=0。在竖向地震作用下，桥梁结构的边界条件为:

接触界面ΓC的位移连续性条件和力连续性条件为:

其中，Qb1和Qb2分别为从左端和右端计算的梁中部的剪力。初始条件为:

2.2 瞬态波函数解

应用瞬态波特征函数法对偏微分方程组(1)进行求解［14～16］。将梁－墩位移分布分解为准静态项和动态项两部分:

其中，准静态解应满足平衡微分方程、真实的边界条件(2)和连续性条件(3)。动态解应满足波动方程(无载荷q)、连续性条件(3)、初始条件(4)和齐次边界条件

最终使解(5)满足波动方程、边界条件、连续性条件和初始条件。根据弹性动力学解的唯一性定理，可以得到图1双跨连续梁桥模型的瞬态波响应的精确理论解。

按照上面所述方法，解得桥梁结构的准静态项us(x，t)为:

在竖向地震响应过程中，梁和杆以共同的特征频率ωn运动，动态位移项可表示成如下形式

其中，梁和杆的波模态函数 φn(x)= ［φbn，φm］T满足特征方程:

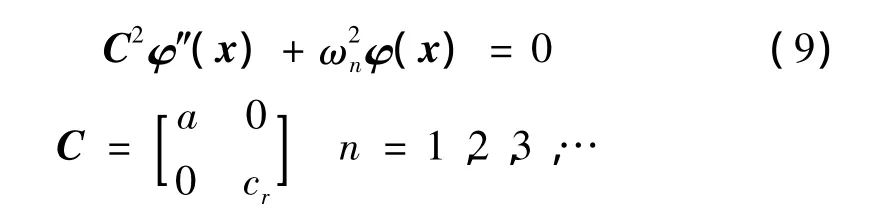
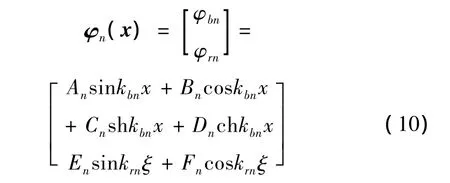
其中，kn=［kbn，krn］TBn，Cn，Dn，En，Fn］T为待定系数。由齐次边界条件列出关于待定系数的线性方程组，根据非平凡解存在的条件，即的系数矩阵行列式为零，导出频率方程为:

将位移解(5)代入波动方程(1)，并应用正交性条件，可导出时间函数的微分方程为:

采用Laplace变换求解可得:

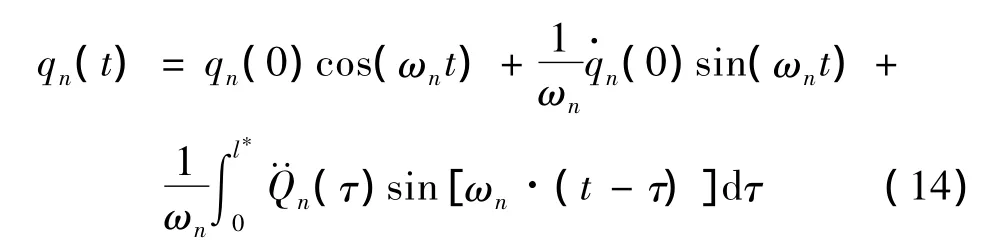
其中，qn(0)和n(0)由地震开始时刻梁和杆的位移和速度分布所确定。

利用公式(5)求出桥梁整体结构的瞬态响应解后，可由接触界面上的应力计算出桥跨结构与桥墩之间的接触力P(t)，计算公式为:

2.3 桥跨结构发生跳起时桥梁响应的计算

陈兴冲等［8］的研究表明，当竖向地震的拉力大于接触面承受的压力时，桥跨结构将发生上跳。在整个地震过程中，反复循环的地震荷载可能造成桥跨结构多次上跳。在本文中，采用文献［17］中提出的计算多次重撞击响应的方法，如果桥跨结构发生上跳，则将整个地震过程分割为交替出现的桥跨结构和桥墩的接触过程和分离过程。由于接触过程和分离过程是不同拓扑的结构，需要分开求解。

由接触过程进入分离过程的条件为接触力为零，即:

而由分离过程进入接触过程的条件为梁和墩在接触处的位移相等，即条件(3a)。

接触过程的计算方法如公式(5)－(15)所述，所不同的是，式(14)中的qn(0)和n(0)是由上一次过程结束时梁和杆的位移和速度分布所确定的。下面主要阐述分离过程的计算方法。

在分离过程中，桥跨结构与桥墩各自独立运动，应分别求解振动响应。其边界条件为:

应用瞬态波特征函数法，解得独立运动的梁和杆的准静态项us(x，t)为:

梁和杆的波模态函数分别为

由齐次边界条件和正交性条件解得

求解时间函数得:

其中，qbm(0)，qrm(0)，bm(0)和rm(0)由上次接触阶段结束时刻的位移和速度分布所确定。

3 竖向地震的瞬态波响应分析

3.1 竖向地震波在桥跨结构和桥墩中的传播

选取竖向地震激励周期T=0.1 s，桥梁所在地区抗震设防烈度为九度。按罕遇地震作用计算［18］，地震波的水平加速度峰值为0.62 g，按照规范取竖向地震波的加速度峰值为水平峰值的2/3，即0.4 g。在竖向地震作用下，在桥跨结构中出现弥散形式的弯曲波，在桥墩中出现非弥散的轴向波。可采用无量纲化长度=ξ/L和=x/x0作为横坐标，以轴力波表达轴向波，以动弯矩波(弯矩减去恒值的静弯矩)表达弯曲波。

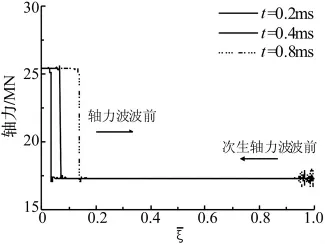
图2 轴力波和次生轴力波的传播Fig.2 Axial force wave and secondary axial force wave

图3 动弯矩波和次生动弯矩波的传播Fig.3 Dynamics bending moment wave and its secondary wave

图2和图3的计算结果表明，当竖向地震在桥跨两端和桥墩底部同时开始激励，则动弯矩波从桥跨的两端向中间传播，轴力波从桥墩底部向顶部传播。计算表明，动弯矩波先于轴力波传播到桥跨的中部，时间大约在0.5 ms左右。此时，轴力波向上传播了1.76 m。动弯矩波在传播到中端后，将与桥墩相互作用，产生两个新的波。一个是新的次生动弯矩波，向桥跨的两端传播，一个是次生轴向力波，向桥墩底部传播。次生动弯矩波与从桥端传播过来的动弯矩波相互作用，产生图3中局部放大图中所示的波干涉现象，使合成动弯矩波产生次振荡。由于桥跨中端与桥墩是力相互作用方式，在桥墩中产生的次生轴力波是由弯曲剪力引起的，它是动弯矩波的导数形式，故振荡比动弯矩波更加明显。

在桥跨中产生的次生动弯矩波与竖向地震激发的动弯矩波相向而行，它在传播到桥跨端部时会出现反射，然后向桥跨中部反向传播，可引起上部结构动弯矩分布的更多振荡。大约在t=3 ms时，桥墩中的轴力波与次生轴力波相碰撞，两波发生相互作用，使得在轴力波波前之后的桥墩中产生高频振荡的轴力变化。但是，轴力波仍然在向桥墩顶传播，并在t=5.77 ms时传播到桥墩顶。

大约在t=5.77 ms时，轴向波传播到桥墩顶，与弯曲波发生碰撞，产生了复杂的波动效应，图4描述了波碰撞后产生的反射轴力波向桥墩底部传播的过程。波碰撞的结果是在桥墩中产生了高幅值的碰撞轴力波，波峰幅值大约为原轴力波幅值的两倍。碰撞轴力波的波形为:先突然上升，然后呈指数衰减，与一般的固体撞击波形相似。碰撞轴力波的峰值近似为原先传播的轴力波的两倍，说明产生了应力加倍效应，该计算结果表明桥跨对于桥墩的约束效应类似于固定端约束效应。

图4 轴向撞击波的传播Fig.4 Impact axial force wave propagation

如图5所示，轴向波与弯曲波发生的波碰撞同样会在桥跨结构中产生向桥两端传播的碰撞弯矩波。碰撞的一个显著结果是:在中部产生了一个高幅值的负的动弯矩，其幅值大约是原最大正动弯矩的两倍。

当t=11.54 ms时，碰撞轴力波前波传至桥墩底部，然后发生反射。当t=17.31 ms时，反射的碰撞轴力波传至桥墩顶，与桥跨中的动弯矩波发生二次波撞击，随即产生二次碰撞轴力波，并从桥墩顶向桥墩底部传播。当 t=17.31+11.54=28.85 ms时，产生了第三次碰撞轴力波。

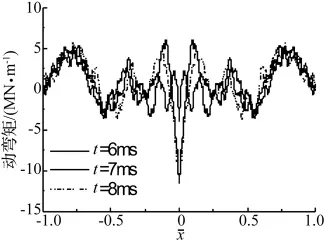
图5 动弯矩撞击波的传播Fig.5 Impact dynamics bending moment wave propagation

以上的计算结果表明，本文方法可以计算竖向地震波在桥梁结构中的传播，描述出地震激励产生的瞬态波的反射、相互作用和波碰撞等波传播现象，从而为合理计算桥梁在竖向地震激励下的结构动态响应提供了理论基础。

3.2 桥跨结构与桥墩的接触力

在前面的计算中，取竖向地震分量与水平地震分量的比值β=2/3。但是，一些危害巨大的重要地震记录显示，竖向地震分量超过了该比值。尤其是在近场地震动记录中，往往出现大幅值的竖向地震动。为此，本文专门选取β为1/2、2/3、1和3/2进行相应的计算分析，来对比研究竖向地震的影响。

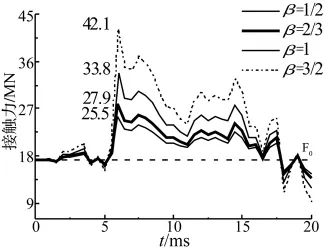
图6 接触力的变化Fig.6 Variations of contact force

图6为地震开始后20 ms内不同β下的接触力的变化情况，图中标记的最大接触力的数值随β的增加近似于线性增加。在5.77 ms之前，接触力在静接触力F0=17.27 MN基础上作小幅振荡。从5.77 ms开始，接触力发生了显著的变化，先是迅速上升，然后振荡下行。由图4可知，该急剧变化的接触力是由于桥墩轴向波和桥跨弯曲波的第一次碰撞所造成的。

从图7中地震开始后0.1 s内接触力的变化情况看，在竖向地震波作用下，接触力不仅会出现明显超过静接触力F0的情况，也会出现明显低于静接触力的情况。超过静接触力过多，会造成支座的损伤;接触力过低，支座接触面的水平摩擦力就会过小，当桥梁受到后继横向地震的共同作用时，桥跨结构滑动的可能性大大增加，从而可能导致落梁现象的发生。大约在β=1时，可能出现零接触力现象，大大增加了落桥的可能性。

3.3 桥跨的跳起现象

图7显示，当β=3/2时，在0.1 s的响应时段内，出现三次接触力为零的短暂时刻，原则上说明桥跨已经与桥墩脱离接触，可能发生了桥跨跳起现象，而该现象在β小于1的时候并没有出现。

图7 0.1 s内接触力的变化Fig.7 Variations of contact force within 0.1 s

观察图8(a)可以发现，当β=3/2时，在0.097 s～0.107 s时段内，桥跨与桥墩的相对分离位移量虽然只有0.056 mm，在实际过程是难以观察到的，但是，出现了接触力明显偏低的一个时段，在该时段内桥跨滑动的可能性大大增加。图8(b)显示，在已考虑上部结构自重的情况下，分离时梁体相对桥墩的加速度大于零，也就是说地震引起的惯性力大于结构自重，所以桥跨结构将发生上跳。

图8 上部结构与桥墩之间的分离Fig.8 Separation between superstructure and pier

3.4 桥墩应力的变化

桥墩中原本保持一致的静态压应力，在竖向地震波作用下出现变化，甚至产生了拉应力截面。对于β=2/3情况，当t=0.816 s时，桥墩中的拉应力达到最大值。根据桥墩截面变形一致性假设，计算出此刻的混凝土的应力沿桥墩高度分布情况如图9所示。

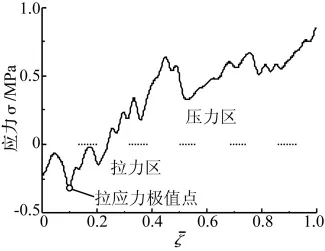
图9 桥墩混凝土应力分布Fig.9 Distribution of axial stress of concrete

计算不同β取值下的桥墩混凝土的最大拉应力可以发现，β的变化不仅会引起最大应力的变化，而且会引起响应特征的改变。当β=1/2时，桥墩中可以认为只有压应力，也就是整个桥墩一直处于受压状态，不会出现混凝土开裂的情况。而在其它β取值下，桥墩中出现了拉应力，整个桥墩出现了拉压交变应力，桥墩的响应特征出现了明显的改变。当β=3/2，即竖向加速度峰值为0.9 g时，最大拉应力为1.80 MPa，发生在桥墩底部，并且已超过了桥墩材料C20混凝土的抗拉强度1.54 MPa，可能导致混凝土开裂。

由于拉－压应力交替出现，可以认为桥墩可能出现多条裂缝，裂缝的间距可计算出为357.1mm。在整个地震作用过程中，拉应力会多次超过混凝土的拉伸强度，在拉－压交变应力的循环作用下，可能造成更严重的破坏，出现桥墩底部混凝土破碎现象［1］。由此可见，对于处在竖向地震幅值较大的近断层位置的桥梁，进行抗震设计时应将竖向地震分量对结构可能造成的损害考虑在内。

3.5 桥跨响应的变化

在不同β取值下，计算桥跨结构最大正弯矩Mmax和最大负弯矩Mmin。最大正弯矩出现在单跨偏桥端3/5处，最大负弯矩出现在桥梁中部。如图10所示，最大正弯矩和最大负弯矩都随β呈近似线性的增加。

图10 最大和最小弯矩随β的变化Fig.10 Comparison of maximum and minimum bending moment in different β

另外，计算出的桥跨的最大动挠度(挠度减去初始时刻的静挠度)分布曲线(图11)表明，随着β的增加，桥梁明显上抬。当β＞1后，桥跨中部向上的动挠度超过两端，也就是桥跨结构被抛起的可能性增大。

图11 最大动挠度随β的变化Fig.11 Comparison of maximum dynamic deflection in different β

4 结论

本文采用瞬态波特征函数法，考虑竖向地震作用下的波动效应，研究了双跨连续梁桥在竖向地震激励下的瞬态动力学响应。计算结果表明，本文方法可以计算竖向地震波在桥梁结构中的传播，描述出地震激励产生的瞬态波的反射、相互作用和波碰撞等波传播现象。对于可能出现高幅值竖向地震加速度的近场地震，按照规范设定的竖向地震动与水平地震动分量的比值β=2/3来计算，可能低估最大接触力，从而低估支座损坏的可能性;同样也可能低估最小接触力，从而低估桥跨与支座间出现滑动的可能性。通过选取不同的竖向地震动与水平地震动的比值β，对比研究了竖向地震可能对桥梁结构造成的影响。数值计算的结果表明:

(1)随着β的增大，最大接触力、桥跨结构最大正弯矩、最大负弯矩和最大动挠度近似线性增大。

(2)在不同的β下，桥墩对竖向地震的响应特征出现了本质性的变化。当β较大时，接触力明显偏低，大大增加桥跨滑动的可能性，并且可能出现了接触力为零的短暂时刻，原则上说明桥跨与桥墩可能脱离接触，有可能发生了桥跨跳起现象。

(3)随着β的增大，原本处于受压状态的桥墩中出现了拉应力，甚至可能超过混凝土的抗拉强度，导致混凝土开裂。整个桥墩出现了拉压交变应力，使桥墩底部处于危险应力状态。

(4)在不同的β下，桥跨结构对竖向地震的响应特征也出现了明显变化。当β较大时，桥跨中部向上的动挠度超过两端，也就是桥跨结构被抛起的可能性增大。

［1］Papazoglou A J，Elnashai A S.Analytical and fileld evidence of the damaging effect of vertical earthquake ground motion［J］. Earthquake Engineering and Structural Dynamics，1996，25:1109－1137.

［2］Yang J，Lee C M.Characteristics of vertical and horizontal ground motions recorded during the Niigata-ken Chuetsu，Japan Earthquake of 23 October 2004 ［J］.Engineering Geology，2007，94:50－64.

［3］Wang D，Xie L L.Attenuation of peak ground accelerations from the great Wenchuan earthquake ［J］.Earthquake Engineering and Engineering Vibration， 2009， 8(2):179－188.

［4］许 强，黄润秋.5.12汶川大地震诱发大型崩滑灾害动力特征初探［J］.工程地质学报，2008，16(6):721－729.

［5］Han Q，Du X L，Liu J B，et al.Seismic damage of highway bridgesduring the 2008 Wenchuan earthquake［J］.Earthquake Engineering and Engineering Vibration，2009，8(2):263－273.

［6］Tanimura S，Mimura K，Nonaka T，et al.Dynamic failure of structures due to the great Hanshin-Awaji earthquake［J］.International Journal of Impact Engineering， 2000， 24:583－596.

［7］Wang C J，Shih M H.Performance study of a bridge involving sliding decks and pounded abutmentduring a violent earthquake ［J］. Engineering Structures， 2007， 29:802－812.

［8］陈兴冲，朱 晞.简支梁桥支座的空间地震反应分析［J］.土木工程学报，1994，27(1):11－18.

［9］Tanimura S，Sato T，Umeda T，et al.A note on dynamic fracture of the bridge bearing due to the great Hanshin-Awaji earthquake［J］.International Journal of Impact Engineering，2002，27:153－160.

［10］王军文，李建中，范立础.非规则梁桥横桥向地震碰撞反应分析［J］.振动与冲击，2010，29(6):25－30.

［11］Chen Y.Modeling and analysis methods of bridges and their effects on seismic responses Theory［J］.Computer＆Structures，1996，59(1):81 －98.

［12］Kappos A J，Manolis G D，Moschonas I F.Seismic assessmentand design ofR/C bridges with irregular congiguration，including SSIeffects ［J］. Engineering Structures，2002，24:1337 －1348.

［13］Lin J H，Zhang Y H，Li Q S，et al.Seismic spatial effects for long-span bridges，using the pseudo excitation method［J］.Engineering Structures，2004，26:1207 －1216.

［14］Yin X C，Qin Y，Zou H.Transient responses of repeated impact of a beam against a stop［J］.International Journal of Solids and Structures，2007，44:7323 －7339.

［15］Yin X C，Yue Z Q.Transient plane-strain response of multilayered elastic cylinders to axisymmetric impulse［J］.ASME Journal of Applied Mechanics，2002，69:825 －835.

［16］Yin X C.Multiple impacts of two concentric hollow cylinders with zero clearance［J］.International Journal of Solids and Structures，1997，34:4597 －4616.

［17］徐 然，尹晓春.竖向地震作用下桥面与桥墩的多次重撞击力的计算［J］.工程力学，2010，27(10):124－130.

［18］周 云，宗 兰，张文芳，等.土木工程抗震设计［M］.北京:科学出版社，2005.