非周期型理想钻柱系统声传播特性研究
2012-09-15张美玲闫向宏刘文丽苏远大陈雪莲
张美玲,闫向宏,刘文丽,苏远大,陈雪莲,路 斌
(中国石油大学(华东)物理科学与技术学院,山东 东营 257061)
近些年发展起来的随钻测井(LWD)是一种功能更齐全、结构更复杂、可以直接观测井下工程参数、及时准确的获取地层资料的随钻测量系统,随钻数据传输是实现自动化、智能化钻井的关键技术之一,它担负着对井下测量参数的上传和地面控制指令下传的双向信息传输任务。目前现场采用的泥浆脉冲数据传输技术和电磁波数据传输技术的数据传输速率仅为几个bit/s。随着随钻测量数据量的不断增加,泥浆脉冲技术和电磁波技术都难以适应随钻大量数据传输的需求,是制约现代钻井技术发展的瓶颈[1-5]。随钻数据声波传输技术是利用沿钻柱信道传播的低频弹性波为载波,将井下测量数据沿钻柱信道传输到地面的一种数据遥传技术,在钻柱信道中弹性波的传播速度大于泥浆中的传播速度,并且可以传播弹性波信号的主频更高,具有更高的载波能力,其传输速率要比现有的泥浆脉冲技术和电磁波技术高出 1 ~2 个数量级[3,6]。Drumheller、车小花、李成等分别采用一维声传播理论、传输矩阵法和有限差分法对周期性理想钻柱系统的声传播特性进行了理论研究[7-11],考虑到实际钻井工程中,钻柱系统往往是由不同规格(长度不同、截面大小不同)的钻杆构成[12],不能简化为单个周期性的结构系统,因此研究非周期型理想钻柱结构系统中的声传播特性,有助于为随钻数据声波传输技术的研究提供理论基础,具有重要工程应用价值。
1 非周期型理想钻柱系统声传播特性理论分析
1.1 非周期型理想钻柱系统频散特性理论分析
在实际的钻井工程中,钻柱系统往往是由不同规格的多根钻杆组成。忽略钻杆与接箍之间的过渡结构,将真实钻柱系统等效为由p个结构周期长度为L=L1+L2的周期性理想钻柱与q个结构周期长度为L'=L3+L4的周期性理想钻柱串联而成的一种非周期型结构,如图1所示。设参数 L1、L3、ρ1、ρ3、S1、S3、C1、C3分别表示钻杆部分长度、密度、截面积和声速,L2、L4、ρ2、ρ4、S2、S4、C2、C4分别表示接箍部分的长度、密度、截面积和声速。

图1 非周期型钻柱系统结构示意图Fig.1 The model of non-periodic drill string system
对于如图1所示的非周期型理想钻柱系统,当声波从左侧传入具有p个结构周期为L1+L2的理想钻柱中,由文献[10]可知,该周期性理想钻柱系统的频散方程为[7]
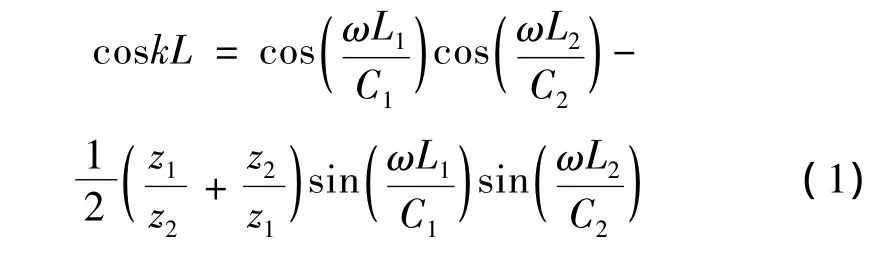
其中z1=ρ1C1S1、z2=ρ2C2S2分别为第一种周期结构中钻杆、接箍的声阻抗。由于周期性理想钻柱的频散特性具有通、阻交替的梳状滤波器特性,频率满足方程(1)阻带条件的声波被结构“过滤”,只有频率满足方程(1)通带条件的声波才能传入到q个结构周期为L3+L4的周期性理想钻柱中,该周期性理想钻柱系统的频散特性由方程(2)给出。

其中z3=ρ3C3S3、z4=ρ4C4S4分别为第二种周期结构中钻杆、接箍的声阻抗,则能传出q个结构周期为L3+L4周期性理想钻柱系统的声波的频率必然满足频散方程式(2)的通带条件。即由p个结构周期为L1+L2的周期性理想钻柱与q个结构周期为L3+L4的周期性理想钻柱串联组成的非周期型结构系统的透射声波频率必须同时满足方程式(1)和(2),可确定出非周期型理想钻柱系统的频散特性。
1.2 非周期型理想钻柱系统声衰减特性理论分析
对图1所示的钻柱系统,当声波从左侧传入时,在截面突变处会产生波的反射与透射。设钻杆中波函数为 φ1=r11eik1x+r12e-ik1x,接箍中波函数为 φ2=r21eik2x+r22e-ik2x,其中rm1和rm2分别表示第m段的透射系数和反射系数[13]。在截面突变处,由波函数连续、体积速度连续可得:
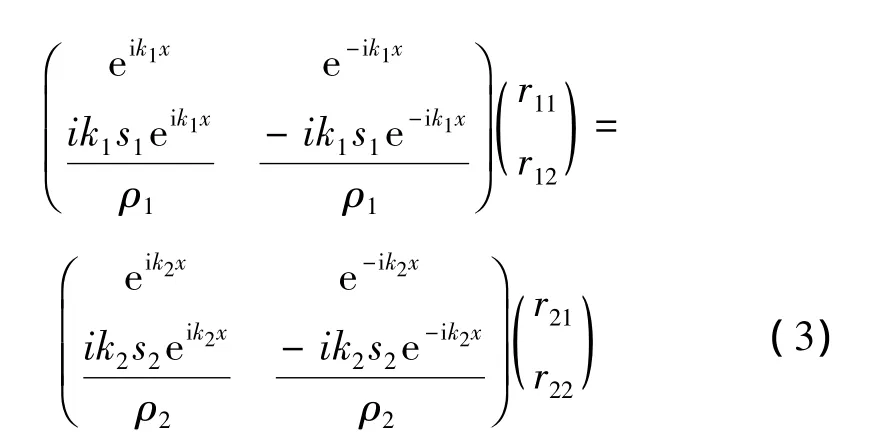
由此可以推出透射波计算表达式为:

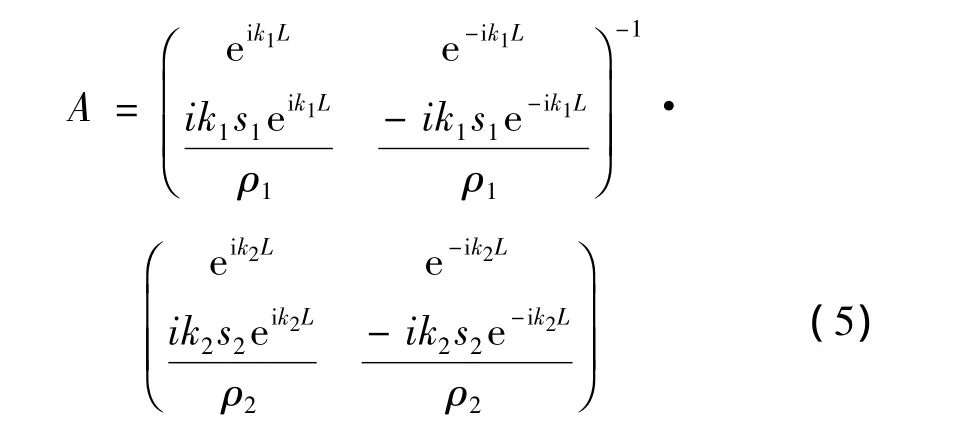
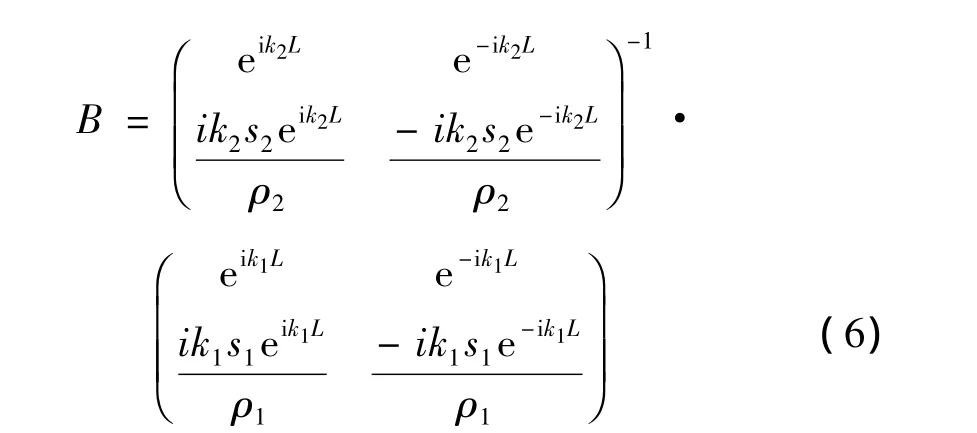
在两种周期结构的衔接部分满足

则整个系统中的波函数可表示为:


其中:

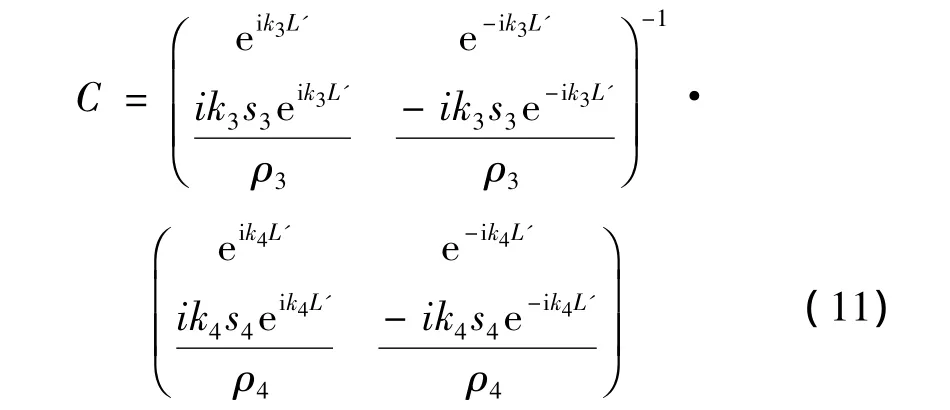
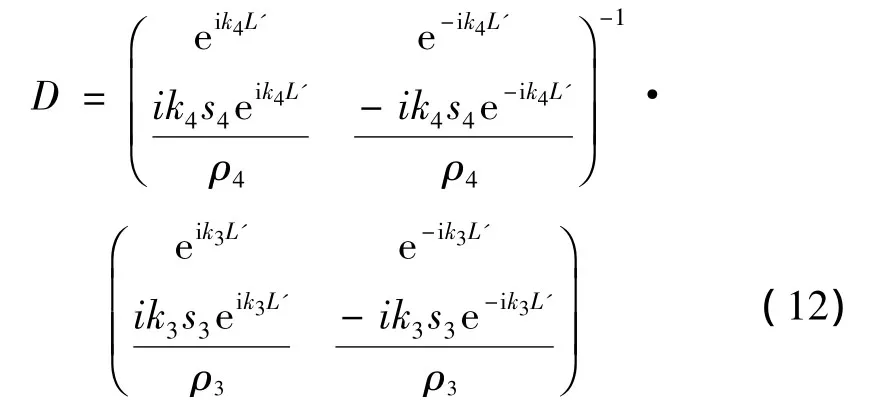
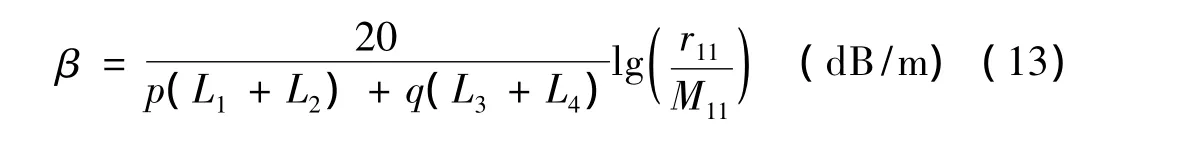
2 数值计算结果与分析
由频散方程式(1)、(2)和声衰减方程式(13)可知,钻杆、接箍的长度和横截面积决定了钻柱系统的声学频带结构及其对声波的衰减特性,计算非周期型理想钻柱系统声学特性时所采用钻柱系统参数如表1所示,其中纵波在钻杆中的传播速度为5 050 m/s,钻柱密度为7 850 kg/m3。

表1 数值计算采用的钻柱系统参数表Tab.1 The parameters of drill string used for numerical calculation
数值计算出钻柱系统在2 kHz~5 kHz范围内的频散曲线和声衰减曲线如图2、图3(a)所示。为了验证理论计算结果,采用表1中参数在有限元ANSYS中建模,对声波沿钻柱系统传播的瞬态特性进行数值模拟,所加载荷为主频3kHz,在1 kHz以下、5 kHz以上幅度衰减为0,-3 dB带宽范围是2.15 kHz ~ 3.84 kHz的高斯脉冲宽带波源,数值模拟得到钻柱上212 m处接收到的瞬态波形如图4所示,对其进行傅里叶变换,得到如图5所示的钻柱系统频谱图,图3(b)所示为利用有限元法计算得到的声衰减曲线。
由图2、图5中的曲线可以看出,周期性钻柱系统的频散曲线呈现通、阻交替出现的梳状滤波特征,当钻柱系统的长度发生改变时,通带、阻带的位置会发生明显变化,长度增加,其通带、阻带位置向低频方向偏移。对于由两种周期性结构串接而成的非周期型钻柱系统,其频散曲线不再呈现通、阻交替的梳状滤波器特征,整体上表现为阻带范围增大,通带范围减小的特征,在2.0~3.7kHz频率段,通带消失,阻带明显增宽,不利于该频段声波在钻柱中的传播。其原因是由于第一种周期结构的通带刚好与第二种周期结构的阻带位置重合造成的。非周期型理想钻柱系统的频散曲线和两个周期性结构频散曲线相“与”的结果一致,并且与有限元数值模拟得到的通带、阻带位置、宽度也符合良好。
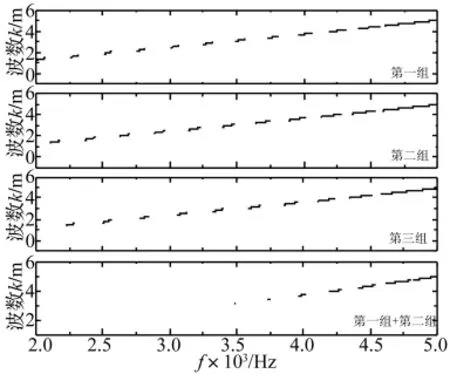
图2 钻柱系统的理论频散曲线Fig.2 The theory dispersion curve of drill string systems

图3 非周期型理想钻柱系统的声衰减曲线Fig.3 Attenuation curve of non-periodic ideal drillstrings

图4 钻柱系统上z=212 m处接收到的时域波形瀑布图Fig.4 The time domain waveform received at z=212 m on ideal drillstrings

图5 理想钻柱上接收波形经FFT变换后的结果图Fig.5 The FFT plot of received waveform on ideal drillstrings
由图3所示的非周期型钻柱系统的声衰减曲线可知,声衰减系数取较大值所对应的频率范围对应其阻带位置,而声衰减系数取较小值所对应的频率范围对应其通带位置,且通、阻带位置与理论计算结果一致。当钻柱中传播声波的频率位于钻柱系统的阻带内时,具有较大的声衰减系数,而位于钻柱系统的通带中时,声衰减系数较小,声波可以传播较长的距离,对利用沿钻柱传播的声波为载波进行随钻数据的传输是非常有利的。因此要想获得较好的数据传输质量,必须根据实际钻井工程中使用的钻柱情况对随钻数据传输的载波频率进行优选。
3 结论
周期性钻柱系统具有通、阻带交替的梳状滤波器特征,钻柱系统长度对其通、阻带的位置影响较大,增加长度,通、阻带向低频方向偏移。非周期型理想钻柱系统的频散特性与多个周期性结构系统频散特性相“与”的结果一致,且具有通带变窄、阻带变宽的特征。当沿钻柱系统传播的弹性载波的频率位于钻柱系统的阻带内时,具有较大的声衰减,当沿钻柱系统传播的弹性载波的频率位于钻柱系统的通带内时,因声衰减系数值较小,能长距离传输,对随钻数据传输是非常有利的。因此在利用沿钻柱传播的弹性声波为载波进行随钻数据传输时,要根据钻井工程中所使用的钻柱系统参数,对载波频率进行优选,同时考虑到钻柱衰减的存在以及钻井噪声的存在,实际中还应提高输入到钻柱系统中的弹性波能量,不仅有助于长距离传输,而且有助于提高信躁比、减小误码率、提高数据传输速率和确保传输数据的质量,基于钻柱系统的随钻数据声波传输测量系统将在非平衡钻井过程中发挥巨大的作用。
[1]李洪强,丁景丽,杨锦舟.地质导向随钻测量数据实时远传系统的设计与实现[J].石油仪器,2005,19(3):8-10.
[2]苏义脑.地质导向钻井技术概况及其在我国的研究进展[J].石油勘探与开发,2005,32(1):92-95.
[3]邹德江,范宜仁,邓少贵.随钻测井技术最新进展[J].石油仪器,2005,19(5):1-4.
[4]方朝亮,吴铭德,冯启宁.测井关键技术展望[J].石油科技论坛,2005(2):32-35.
[5]王 若.随钻测井技术发展史[J].石油仪器,2001,15(2):5-7.
[6]张辛耘,王敬农,郭彦军.随钻测井技术进展和发展趋势[J].测井技术,2006,30(1):10-15.
[7]Drumheller D S.Acoustical properties of drill strings[J].J.Acoust.Soc.Am.,1989,85(3):1048 -1064.
[8]Drumheller D S.Attenuation of sound waves in drill strings[J].J.Acoust.Soc.Am.,1993,94(4):2387 -2396.
[9]车小花,乔文孝,李 俊,等.随钻测井钻柱声波的频谱特性[J].中国石油大学学报(自然科学版),2008,32(6):66-70.
[10]李 成,丁天怀.不连续边界因素对周期管结构声传输特性的影响[J].振动与冲击,2006,25(3):172 -175.
[11]李 成,丁天怀,陈 恳.周期性管结构信道的声传输方法分析[J].振动与冲击,2009,28(2):12 -15.
[12]李子丰,张永贵,侯绪田,等.钻柱纵向和扭转转动分析[J].工程力学,2004,21(6):203-209.
[13]沈建国,富伟平.声波测井仪器接收换能器隔声设计[J].石油仪器,2005,19(5):8-10.
