动态载荷激励位置识别技术研究

祝德春，张 方，姜金辉

(南京航空航天大学 机械结构力学及控制国家重点实验室教育部重点实验室，南京 210016)

近年来，随着人类对结构动力学研究的进一步加深，动态载荷识别技术也得到了快速发展。现今为止，比较成熟的动态载荷识别技术是频域法和时域法，一些新兴的如基于神经网络和遗传算法的动载荷识别方法也逐渐发展起来，桥梁移动载荷识别技术［1］也得到了很好的发展。以往这些研究，大都是在已知载荷激励位置的情况下进行的识别。例如，Bartlett和Flannelly［2］对直升机桨毂中心动载荷识别方法研究展开了模型验证，开创了动态载荷识别的先河。英国帝国学院Ewins和Hillary［3］较系统地建立了频域载荷识别方法。在冲击载荷位置识别方面，国内外学者也开展了一些研究。东京工业大学Inoue等［4］应用Gabor小波分解技术将时域散射波作时频变换，通过确定各频率弯曲波在梁内传播的时间来确定冲击位置。德国Stuttgart大学Gaul和Hurlebaus［5］等基于小波变换，通过确定不同频率弯曲波的到达时间和与优化方法相协同的技术，识别了冲击作用位置。以上两种方法利用了小波的时频分析特性，能够较好的确定振动波的传播时间和频率分布情况，但是对于振动传递路径复杂的复杂模型仍然难以实现载荷位置的识别。周晚林等［6］将神经网络和反分析法相结合，提出了用于反求载荷位置的有限元逆逼近方法，用于识别载荷位置。严刚、周丽［7］将冲击载荷识别问题转换为优化问题，以模型计算结果与实际量测信息之差作为最小化理论目标函数，提出了一种基于遗传算法自适应搜索的冲击载荷识别方法。对冲击时刻未知和量测信息缺失的情况，他们还提出了一种同时识别冲击时刻和冲击位置并近似重建冲击载荷历程的方法［8］。但是，他们的方法不足之处在于难以保证优化过程中的每一步计算都能顺利获得准确的振动响应(即计算任意位置的振动响应)，另外量测数据的真实性与可靠性也是影响载荷识别正确与否的重要因素。侯秀慧等［9］基于HPD－S格式的精细积分法，建立了梁上移动载荷识别方法，提高了大步长情况下移动载荷的识别精度。张方等［10］研究了基于有限元模型的复杂结构分布动载荷识别问题，为复杂结构确定性分布的稳态振动载荷识别奠定了基础。

本文通过对简支梁振动特性进行研究，根据动态载荷识别频域法(以下简称频域法)的基本原理，采用梁上任意两组不同振动响应在载荷作用位置处识别的一组动载荷在量值上相等的原则，提出了梁上动态载荷激励位置识别的“最小判定系数法”。

1 载荷识别频域法

所谓频域法，就是指用频响函数和结构系统的响应信息求解系统外载荷的方法。一种频响函数矩阵求逆法，即假设系统所需确定的载荷数为P，响应的测点数为L，则有载荷与响应之间的关系:

其中，X(ω)为响应谱向量，F(ω)为载荷谱向量，H(ω)为频响函数矩阵，式(1)写成复数形式为:

若待定的载荷数与响应的测点数相等，即L=P，则H(ω)为方阵，式(2)的求解在理论上非常简单，由下式即可求得:

在L＞P的情况下，H(ω)不是方阵，则对频响函数求广义逆，此时载荷识别的公式就变为:

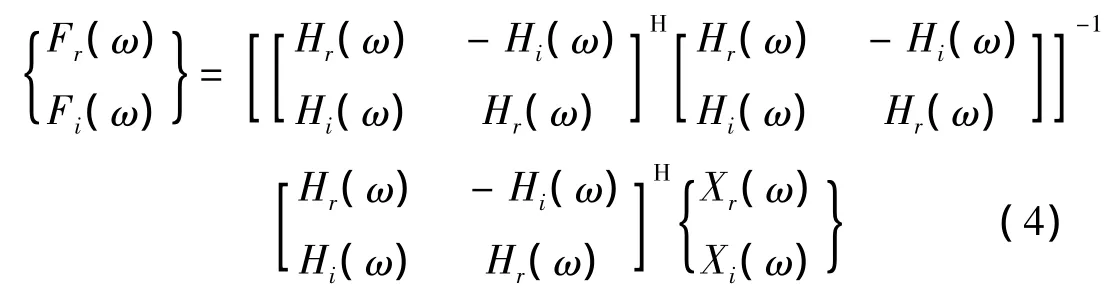
该方法思路简单，通过优化选取响应测点，可以有效地识别动态载荷，其工程应用较为广泛。

2 简支梁动力学模型

建立简支梁模型如图1所示。

图1 简支梁模型图Fig.1 The model of simply supported beam

假设该模型为Bernoulli-Euler梁(不考虑剪切变形与转动惯量的影响)，具有均匀横截面A，且质量均匀分布(单位长度梁的质量ρ为常数)，截面弹性模量为E，截面惯性矩为I，梁的运动满足小变形理论并在弹性范围内，则其动力学运动方程为:

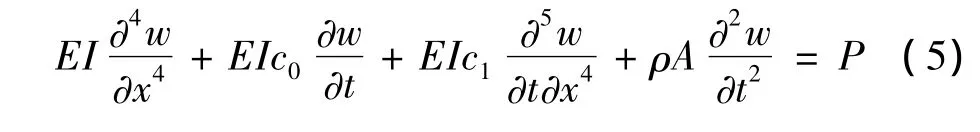
其中，w=w(x，t)为梁的横向变形，c0为梁的外部介质阻尼系数，c1为梁的内阻尼系数，P为梁所受的外载荷向量。

根据模态叠加理论，梁的横向变形可表示为:

其中qr(t)为第r阶广义模态坐标，φr(x)为第r阶模态阵型，对于简支梁，可用如下形式表示:

根据模态正交性，式(5)可以变换为模态空间下解耦的微分方程组:

由式(8)可得梁上xa处激励，任意位置的频响函数为:

通过仿真计算或实验测试获得响应测点与外载荷激励点之间的频响函数，构造载荷识别标定矩阵，根据频域法，即可识别出动载荷的幅值大小。

3 动载荷位置识别的最小判定系数法

根据梁的振动特性，在梁上某一点或几点作用集中载荷时，梁上任意点的响应是唯一的。因此，识别动载荷激励位置时，在排除结构对称性影响的情况下，任意假定一组载荷可能的作用位置，称之为虚拟激励位置，再在梁上选取一组动响应，则根据频域法可以识别出一组当量动载荷，记为当量动载荷一;再选取另外一组响应，同样可以识别出一组当量动载荷，记为当量动载荷二。理论表明，当虚拟激励位置位于载荷的真实激励位置时，识别出的两组当量动载荷量值相等。实际上，由于标定矩阵以及响应信息的噪声和量测误差难免存在，使得两组当量动载荷在数值上往往存在微小的差别。此时，可以将动载荷激励位置识别问题转化为求满足两组当量动载荷差值最小时所对应的假设激励位置的最优化问题，即本文提出的“最小判定系数法”。

假设梁上动载荷个数为N，根据两组响应可以识别一组载荷激励位置的原则，所需的响应个数为L≥2N。实际上，只要从可测的响应中，依据频域识别法的基本原理，选取并构造两组不完全相同的响应向量，即可识别载荷激励位置。以载荷数N=2为例，通常情况下识别2个动载荷至少需要2个响应，即2个响应构成一组用于识别的响应向量。那么，此时，在梁上选取3个不同位置的响应，从中任意选取两个响应组成元素不完全相同的响应向量即可进行动态载荷激励位置识别。

从而，从L个响应中选取M(M≥N)个响应构造成一组响应向量，根据频域法识别理论有:

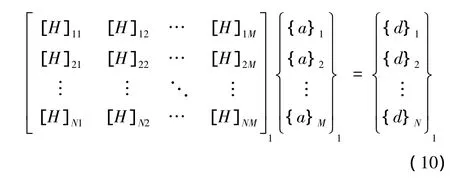
为了建立载荷激励位置的识别模型，需从L个响应中选取另外M(M≥N)个响应作为另一组识别响应向量，同样可以识别出一组当量动载荷:

为描述方便，将(10)、(11)两式简记为:

则在频域下识别载荷激励位置的问题就转化为求两组当量动载荷差值最小的优化问题，最优化函数可用如下表达式表示:

式(14)即为识别载荷激励位置的最优化函数表达式，Coe称为判定系数，当 x=xi，i=1，2，…，N 时，即虚拟激励位置位于梁上 xi时，对应的判定系数为Coe(xi)。每取一组虚拟激励点，就可获得一个(或一组)判定系数，判定系数最小值对应的虚拟激励位置即为载荷的真实激励位置。

通过式(14)识别载荷激励位置的关键是当对任意一个假设激励位置进行识别计算的时候，要求能够准确地获得其频响函数值。通常情况下，通过模型的动力学运动方程可以准确地计算出任意位置的频响函数，从而可以比较方便地识别出载荷激励位置。但是，对工程中的复杂结构，建立一个准确的数学模型是相当困难的，通常需借助数值计算的手段如有限元法来解决这个问题。本文以简支梁为例，探讨了有限元技术在动载荷激励位置识别中的应用。

利用有限元技术将梁离散成若干个自由度，则每个单元上的节点(简支端外除外)即为假设的激励位置，在MSC Patran＆Nastran中建立有限元模型并计算各虚拟激励点与响应测点之间的频响函数。通常情况下，虚拟激励点可以根据经验作出选择，否则，将整个模型上所有节点作为虚拟激励点。确定虚拟激励点后，根据式(14)依次计算载荷位置识别的判定系数。

4 仿真算例与实验验证

4.1 简支梁仿真算例

图2为一简支梁有限元模型，该梁长l=1 m，宽a=0.02 m，高 h=0.03 m，泊松比 μ =0.3，弹性模量E=210 GPa，密度 ρ=780 kg/m3。在距梁右端 0.3 m处施加一个幅值250 N、频率51.5 Hz的正弦载荷。

图2 简支梁有限元模型Fig.2 FEM model of simply supported beam

将该梁划分为20个单元，共21个节点，除简支端两个节点外，假设其余19个节点均为可能的激励点，将距梁左端0.2 m和0.4 m处对应的节点的振动加速度响应作为识别的响应，根据式(14)对该简支梁上的载荷激励位置进行识别。识别的判定系数变化曲线如图3所示。

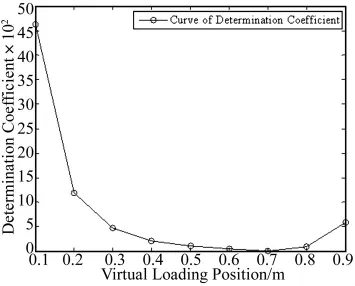
图3 判定系数变化曲线Fig.3 Curve of determination coefficient

由图3可见，最小判定系数对应的节点位置距梁左端0.7 m，与载荷激励位置相同，最小判定系数为0.837 5，识别成功。

4.2 动态载荷激励位置识别实验

上文通过仿真计算，对动载荷激励位置识别方法进行了验证，本文现结合简支梁动态载荷位置识别技术的实验研究，探讨了识别方法工程应用的可行性。

如图4所示，一铝质矩形梁，两端简支，长l=0.68 m，截面宽 a=0.05 m，厚 h=0.008 m，弹性模量 E=70 GPa，泊松比 μ =0.3，材料密度为 ρ=2 590 kg/m3。建立有限元模型，将其划分成16个单元共17个节点，如图5所示。

图4 简支梁实验模型Fig.4 Experimental model of simply supported beam

图5 实验简支梁有限元模型Fig.5 The FEM model of Experimental beam

根据实验获得的频响函数，对该梁的有限元模型进行修正，修正后前五阶固有频率的计算值与实验值如下表:

表1 固有频率对照表(单位:Hz)Tab.1 Natural frequency of the beam(Unit:Hz)

(1)在梁上5号节点和9号节点对应位置处分别施加频率为120 Hz、相位为零的正弦载荷。排除两简支端受载荷作用的情况，以2－16号节点作为虚拟激励位置，以10、12和15号节点为响应测点。根据式(14)进行动态载荷位置识别，识别的判定系数变化曲线如图6所示。

从位置识别判定系数变化曲线可以看出，最小判定系数组合为［0.012 0，0.007 4］，对应的节点号组合为［5，9］，分别为梁上距梁左端 0.17 m 和 0.34 m 的载荷真实作用位置，识别结果与实际激励位置吻合。

(2)在梁上4号节点和8号节点对应位置处分别施加频率为120 Hz和180 Hz的正弦载荷，以除简支端外的15个节点作为虚拟激励点，响应测点为3、6、10和14号节点对应的位置。根据式(14)进行识别，识别结果如图7和图8所示。

图6 判定系数变化曲线Fig.6 Curve of determination coefficient

图7 载荷一位置识别判定系数变化曲线Fig.7 First curve of determination coefficient

图8 载荷二位置识别判定系数变化曲线Fig.8 Secend curve of determination coefficient

频率为120 Hz的载荷，其激励位置识别的最小判定系数为0.011 5，对应节点4所在的位置;频率为180 Hz的载荷识别的最小判定系数为0.002 6，对应节点9所在的位置。识别结果与实际加载位置相同，识别成功。

5 结论

本文提出的“最小判定系数法”，通过对结构上动态载荷分布区域进行预估计，结合有限元模型，选取虚拟激励组合并择优选取响应测点，根据识别规模建立一对振动响应组合。通过计算各虚拟激励点组合对应的判定系数，以最小判定系数(或最小判定系数组合)为目标，该目标对应的虚拟位置(或虚拟位置组合)，即为载荷的真实激励位置。仿真和实验结果证明，“最小判定系数法”原理简单，能够达到识别结构动态载荷激励位置的目的。

［1］Yu L，Chan T H T.Recent research on identification of moving loads on bridges［J］.Journal of Sound and Vibration，2007，305(1 －2):3 －21.

［2］Bartlett F D，Flannelly W D.Model verification of force determination for measuring vibration loads［J］.Journal of the American Helicopter Society，1979:10 －18.

［3］Hillary B，Ewins D J.The use of strain gaugesin force determination and frequency response function measurements［C］.Proceedings of the 2nd International Modal Analysis Conference(IMAC)，Florida，USA，1984:627 －634.

［4］Inoue H，Kishimoto K，Shibuya T.Experimental wavelet analysis of flexural waves in beams［J］.Experimental Mechanics，1996，36(3):212 －217.

［5］Gaul L，Hurlebaus S.Identification of the impact location on a plate using wavelets［J］.Mechanical Systems and Signal Processing，1997，12(6):783 －795.

［6］周晚林，王鑫伟，胡自立.压电智能结构载荷识别方法研究［J］.力学学报，2004，36(4):491 －495.

［7］严 刚，周 丽.加筋复合材料结构的冲击载荷识别［J］.航空学报，2008，29(5):1150 －1156.

［8］严 刚，周 丽.冲击时刻未知情况下复合材料结构冲击载荷识别［J］.中国机械工程，2009，20(1):99 －103.

［9］侯秀慧，邓子辰，黄立新.基于精细积分方法的桥梁结构移动载荷识别［J］.振动与冲击，2007，26(9):142 －145.

［10］秦远田，张 方.具有连续分布梁模型动载荷的识别技术研究［J］.振动工程学报，2005，18(2):126 －128.