基于非负矩阵分解与主元分析的时频图像识别方法研究
2012-09-15李宏坤陈禹臻张志新
李宏坤,陈禹臻,张志新,周 帅
(1.大连理工大学 机械工程学院,大连 116023;2.大连理工大学 工业装备结构分析国家重点实验室,大连 116023)
时频分析方法是对非平稳、非线性信号进行分析的有效方法。机械振动所构成的时频图像含有描述机械工作状态的特征信息[1]。为高效率地处理存放于像素矩阵中的数据信息,一般采取将矩阵进行分解的方法。分解后可以对原始矩阵中存放的大量数据进行压缩和概括,进而对压缩矩阵进行特征提取,得到机械设备的状态信息。非负矩阵分解(Non-negative Matrix Factorization,NMF)[2]是目前国际上新的矩阵分解方法,并在理论和应用方面已相对成熟。较完整的NMF理论由Lee等[2]提出,并应用于人脸识别,这引起了科学界的广泛关注。常用的矩阵分解方法有:主成分分析(PCA)、矢量量化(VQ)等。在所有这些方法中,原始的大矩阵V通过V=WH被近似分解为低秩的形式。这些方法的共同特点是:计算机的“认知”过程是基于数据整体的过程,即因子W和H在线性组合时可进行加运算,亦可进行减运算。这样即使输入的初始矩阵元素是全正的,分解后的结果也不能保证非负性。然而负值元素在实际问题中往往是没有意义的[3]。例如图像数据中不可能有负值的像素点,在文档统计中负值也是无法解释的。因此,探索矩阵的非负分解方法一直是很有意义的研究问题。正是如此,NMF方法才得到人们的广泛关注。非负矩阵分解以计算机的“认知”过程是基于部分的过程为前提,通过添加“线性组合时只允许加运算不允许减运算”的限制条件,保证了分解结果的可解释性。与PCA和VQ相比,NMF数学实现简便、分解形式和分解结果上的可解释、以及占用存储空间少[4],更重要的是非负限制与联系部分形成整体的直觉概念是协调的,这与智慧生命对事物感知的生理过程是相符的[2]。目前它已广泛应用于诸多领域。
蔡蕾等[5]提出了基于图像识别的设备运行状态识别方法,并初步研究了稀疏性非负矩阵分解中各参数对识别率的影响。本文根据设备故障诊断中实际存在的问题,研究采用Hilbert时频谱构建图像,应用非负矩阵分解和主元分析对其进行特征向量提取,完成状态的识别。并以滚动轴承在不同状态下的识别为例验证方法的有效性。
1 非负矩阵分解及PCA降维
1.1 NMF定义及算法实现
非负矩阵分解使计算机对整体的认知是基于其部分的认知。其定义为[2,6]:给定一个n×m图像矩阵V,其每一列都是一组图像数据,并且包含n个非负像素值。为了估计原始图像矩阵,需要寻找两个非负矩阵因子 W∈Rn×r和 H∈Rr×m,使得:

式中:W中的r列数据构成基本图像序列组,H中的每一列被认为是一个由构成V中每一个图像的基本图像的线性组合系数组成的编码且与在V中的每一个图像序列一一对应。因数分解中r值的选择通常满足:
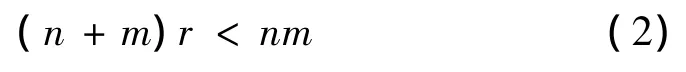
WH的乘积即可被认为是V中数据的压缩形式。线性组合只允许加法运算而不允许减法运算的约束将导致分解具有非负性。
NMF的求解问题实际上是一个最优化问题,并利用乘性迭代的方法求解W和H。以W和H的非负性为初始条件,通过使目标函数F收敛至局部最大,得到非负矩阵V的近似分解[7]。本文使用的目标函数定义为 KL 散度(Kullback-Leibler divergence)[8]:
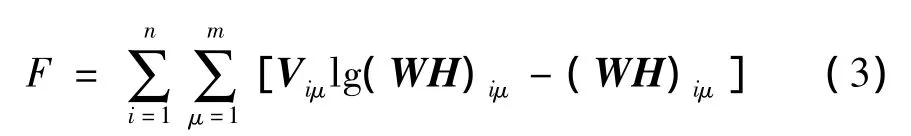
其中:分解矩阵W和H的更新法则如下:
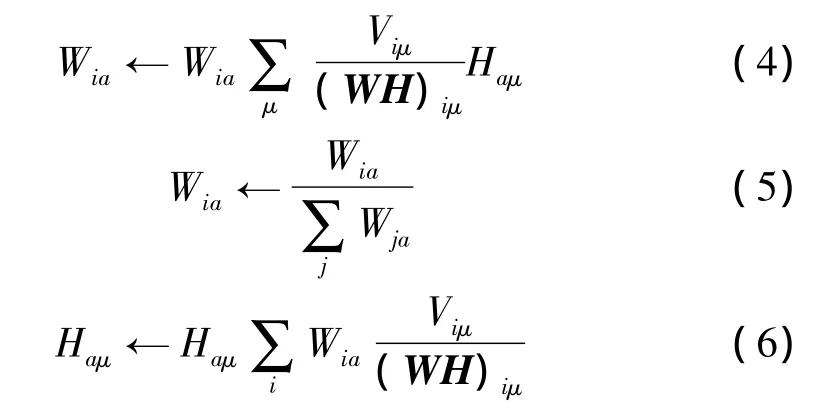
当该目标函数达到局部最大值时,得到非负矩阵V的最优近似分解。分解的精确性通过控制Viu与(WH)iu的商值来参与更新过程。更新法则不但维持着W和H的非负性,而且能有效杜绝W列上数据的“退化”现象。
1.2 PCA降维简介
PCA方法是一种基于二阶统计的数据分析方法。该方法通过对各个变量之间相关关系进行分析,用一组较少的、互不相关的、尽可能多地保留原来复杂变量所反映信息的主元变量来代替原来较多的变量,从而实现对数据的降维。这种方法可以有效地找出数据中最“主要”的元素和结构,去除噪音和冗余,将原有的复杂数据降维,揭示隐藏在复杂数据背后的简单结构。它的优点是简单,而且无参数限制,可以方便的应用于各个场合[9-10]。
2 基于NMF和PCA的状态识别
傅里叶变换对非平稳与非线性信号进行频谱分析往往得不到理想的效果。因此,为精确的描述这些非稳定信号的局部信息,时频分析方法得到广泛的重视和研究。时频方法得到的结果往往可以用图像的形式(如轮廓图像、灰度图像、浮雕图像)表达出来。因此故障诊断实质上是对图像的分类:如果图像分类正确,则可正确的识别故障。关于对图像的分类,传统的方法是人工判断,这将在故障诊断中引入主观因素。而用计算机自动处理(如智能识别系统)时,往往由于图像数据的尺寸和维数太大而无法进行处理。因此,对图像在其信息尽可能完整的条件下进行降维是非常必要的。
由于图像像素的非负性,传统的降维方法如主成分分析(PCA)、矢量量化(VQ)等方法的应用效果往往不是很理想。而加入非负限定条件的NMF能很好的解决上述问题。根据设备故障诊断的实际特点,本文采用Hilbert时频谱构建时频图像,应用非负矩阵分解与主元分析方法进行特征提取和状态识别。本方法的流程图如图1所示。
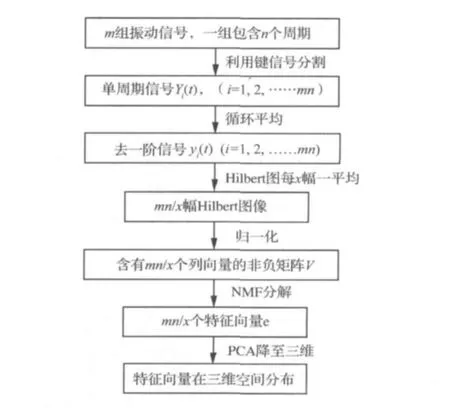
图1 基于NMF和PCA的设备状态识别方法流程图Fig.1 Flow chart for classification based on NMF and PCA
此方法能够有效对包含设备故障信息的振动信号进行表征。采用NMF方法能够获取其主要特征向量从而提高识别的可靠性,PCA能够进行有效降维,便于实际设备故障诊断的应用。
3 实验测试
3.1 实验数据
本文采用的数据来自于大连理工大学振动工程研究所的多功能故障诊断试验台进行的滚动轴承故障模拟实验。模拟的工作状态主要有正常、外环磨损、内环磨损和滚动体磨损四种。每个状态共采集了125组数据,一组数据包含4个周期,即每个状态包含了500个周期的数据。滚动轴承的型号为N205,转速为1 200 r/min。关于本实验对振动信号采集的要求、获得单周期信号Yi(t)的方法以及循环平均以得到去一阶信号yi(t)的过程见文献[11]。
3.2 Hilbert时频谱分析
Hilbert时频谱是利用瞬时频率进行信号时频分析的方法[12]。将滤去一阶的信号yi(t)进行Hilbert时频谱分析。为了削弱噪声的干扰、突出故障信息,可以对时频谱进行平均,本文采用5幅Hilbert图像平均的方法。这样每种情况将得到100组Hilbert时频谱图像。图2为平均后不同状态下的Hilbert时频谱。

图2 不同状态的Hilbert时频图像Fig.2 Different Hilbert Time-frequency image
由图2可知,各工作状态下的Hilbert时频图像并无明显可区分特点,因此单单依靠Hilbert时频谱是无法进行状态识别的。鉴于Hilbert时频图像含有丰富的状态信息,为提取有用信息,需对其进行进一步的图像处理。降低;r值选取过大时,则可能带入多余的冗余信息和噪声。当r值为45时,平均识别成功率达到最大[13]。因此本文r选择45。则每种情况将得到100组维数为45的特征向量ei。
4 基于NMF和PCA的状态识别
4.1 特征向量的提取
在图像处理之前,要对Hilbert时频图像(为201×479的矩阵)进行真彩化和归一化处理(这样可以减小特征向量不同量级之间差异的影响,提高训练和预测的准确性)。
将真彩化和归一化处理后的矩阵(201×479)表示成一个96279维的列向量。每种状态(正常、外环磨损、内环磨损和滚动体磨损)都有100个图像数据。由100组96 279维的列向量构成96279×100矩阵V作为非负矩阵。经非负矩阵分解后,得到矩阵因子W和H,满足V≈WH。W的列向量可认为是组成原图像矩阵V的基本图像。将代表信号图像的96 279维列向量vi与W进行线性组合,即ei=WTvi。这样,r维向量ei即可认为是该幅信号图像vi的特征向量。其中r的值满足式(2),即 r<99.896。
非负矩阵分解r值的选取至关重要。r为描述原始图像矩阵基本图像的个数以及得到的特征向量的维数。r值选取过小时,得到的基本图像不足以描述原始图像矩阵,因而向基投影后部分信息丢失,导致识别率
4.2 利用欧式距离分离各种状态
欧式距离是图像识别中经常采用的方法,因此本文首先采用欧式距离对不同状态下的故障进行判别。从上述四种情况的100个特征向量中随机各选一个向量作为参考向量,分别命名为 ball,inner,normal,outer。将特征向量组矩阵NMF(NMF矩阵由45×400构成,其中1~100列、101~200列、201~300列、301~400列分别是滚动体磨损、内环磨损、正常、外环磨损的特征向量)的每一列与上述四个参考向量分别作欧式距离。当对应情况的欧式距离最小时则识别成功,图3为识别结果。

图3 欧式距离识别结果Fig.3 Classification result by using euclidean distance
从图3可以看出,除对正常情况识别成功以外,其余都不理想。这说明虽然特征向量的维数较大时,可以较全面的反应原始图像的特征信息,但维数的增加并不利于利用特征向量进行状态识别。所以在状态识别之前对特征向量进行降维变得非常必要。
4.3 基于PCA的降维处理
由于PCA的诸多优点(如前所述),本文采用PCA方法对特征向量进行降维处理。经过PCA处理,将NMF处理得到的400组维数为45的特征向量ei降维成维数为3的特征向量ei'。通过上述的数据处理,得到正常、外环磨损、内环磨损和滚动体磨损四种情况分别对应的特征向量组。每种情况对应100组维数为3的特征向量。将降维后的特征向量组矩阵命名为PCA(PCA矩阵由3×400构成,其中1~100列、101~200列、201~300列、301~400列分别是滚动体磨损、内环磨损、正常、外环磨损降维后的特征向量)。本文将一个三维特征向量当作三维空间中的一个点并利用三维坐标系来分离不同的状态,图4、图5为特征向量在三维坐标系上的反映。可以看出,正常、外环磨损、内环磨损和滚动体磨损四种状态被识别的非常清楚。正常、外环磨损和滚动体磨损的分布区域依次链状分布,而内环磨损的点则成环状围绕在链的周围。因而解决了只采用Hilbert时频谱识别故障状态不理想的问题,也解释了欧式距离无法识别状态的原因。
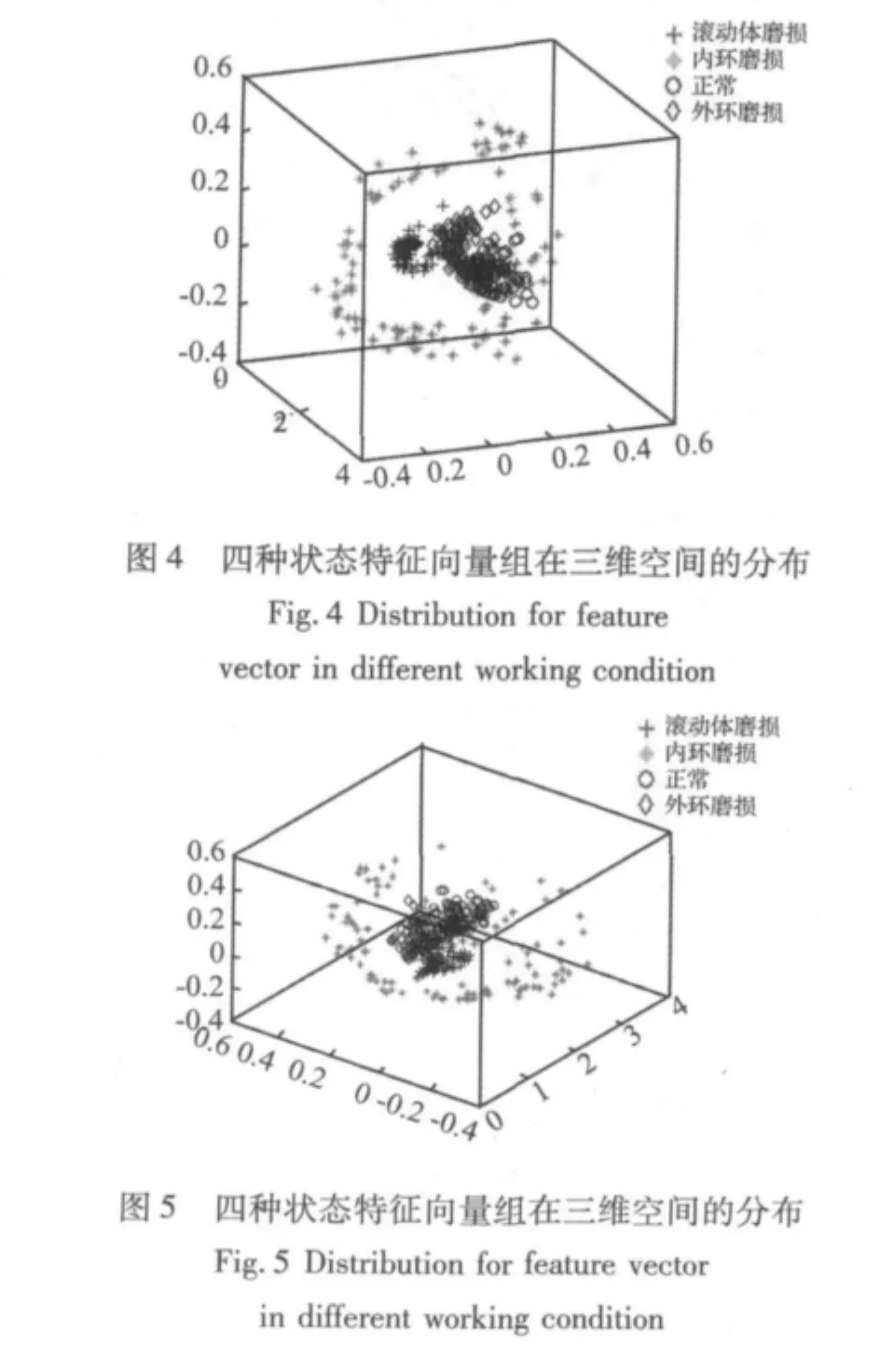
因此经过主元分析之后可以有效获取识别向量作为参数进行设备的状态识别,此方法可以为以后的状态辨识研究打下坚实的基础。
5 结论
本文研究了基于NMF的时频图像特征提取与PCA降维进行振动信号特征提取与状态识别的方法,并采用滚动轴承信号的故障诊断进行方法的有效性验证。通过对比,此方法在识别滚动体磨损等冲击现象不明显的故障状态时比Hilbert时频谱更为有效。此方法的研究将有助于设备故障诊断和预知维修的发展。
[1] Newton R E.Fragility assessment theory and practice[R].Monterey Research Laboratory, Inc. Monterey,Califonia,1968.
[2] Lee D D,Seung H S.Learning the parts of objects by nonnegative matrix factorization [J].Nature,1999,(401):788-791.
[3] Paatero P,Tapper U.Positive matrix factorization:a nonnegative factor model with optimal utilization of error estimates of data values[J].Environmetrics,1994,5(2):111-126.
[4] 汪 鹏.非负矩阵分解:数学的奇妙力量[J].计算机教育,2004(10):38-40.
[5] 蔡 蕾,朱永生.基于稀疏性非负矩阵分解和支持向量机的时频图像识别[J].自动化学报,2009,35(10):1272-1277.
[6] Lee D, Seung H. Algorithmsfornon-negative matrix factorization[M].USA:NeuralInformationProcessing Systems(NIPS).Denver,CO,2000,7.
[7] Lee D D,Seung H S.Algorithms for non-negative matrix factorization[C].Advances in Neural Information Processing Systems.Cambridge:MTT Press,2000:556-562.
[8] 李 乐,章毓晋.非负矩阵分解算法综述[J].电子学报,2008,36(4):737-743.
[9] Jolliffe I T.Principal component analysis(2nded)[M].New York:Springer,2002.
[10] He Q B,Yan R Q,Kong F R,et al.Machine condition monitoring using principal component representations[J].Mechanical Systems and Signal Processing,2009,23(2):446-466.
[11] 李宏坤,周 帅,黄文宗,基于时频图像特征提取的状态识别方法研究与应用[J].振动与冲击,2010,29(7):184-188.
[12] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of The Royal Society of London Series A-Mathematical Physical and Engineering Sciences,1998,454:903- 995.
[13] 宦若虹,杨汝良.基于小波域NMF特征提取的SAR图像目标识别方法[J].电子与信息学报,2009,31(3):588-591.
