渡槽桩－土－槽墩相互作用模型模态实验研究

卢 剑，李正农，朱旭鹏，张盼盼，李继孟

(1.湖南大学 建筑安全与节能教育部重点试验室，长沙 410082;2.云南省设计院，昆明 650032)

南水北调工程是我国继三峡工程之后又一个宏伟的水利工程，其对于华北地区在21世纪的经济、社会发展有着重大的意义［1］。该工程途经的河北省是地震多发地区。在这些地区所兴建渡槽的抗震能力，是一个非常重要的并且值得深入研究的问题。渡槽结构与桩的模态分析是渡槽结构地震反应计算和抗震设计的基础［2］。桩的振动理论是桩基抗震、防震设计的基本依据，也是桩的各种动测方法的理论基础。目前对上部结构的模态试验技术和方法已经非常成熟，由于桩位于地下，对其进行模态实验多有不便。但是对于桩模态研究还停留在数值模拟阶段，缺少试验的验证。仅赵伟封［3］采用标准砂和铁砂模拟桩周土，以此为模型对桩进行了模态实验。本文采用自制的装置，首次对打入实际土层渡槽模型钢管桩进行模态实验，并用有限元软件计算结果进行比较，得出了一些有益的结论。

在地基－基础－上部结构相互作用方面，国内外已经进行了较多的研究。周云等［4］对一座采用柱下独立基础的钢筋混凝土4层框架结构进行了随着层数增加的4种工况模态实验，用脉冲锤击法测试得到了各种工况的整体模态频率和振型。得出结论:考虑地基－基础－上部结构动力相互作用，考虑土结构动力相互作用条件下的物理参数识别和地基参数识别具有重要的意义。王博等［5］采用集中弹簧模型来考虑土－结构动力相互作用，进行渡槽结构的动力响应分析。杨世浩等［6］采用等效弹簧模拟土体对桩的作用，对洺河渡槽进行耦合动力分析。本文用有限元软件ABAQUS的实体模型近似地模拟土体，把实验测获得的土体参数赋予土体模型进行计算，得到了与试验结果较吻合的结果。

1 模态分析的数学模型

将结构离散化为若干自由度后，在物理坐标系统中，N个自由度的系统的方程为:

式中:

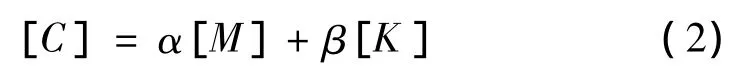
其中，α和β为比例常数，［C］称为比例阻尼。进行相同的变换:

式中:{φr}为由所确定的第 r阶模态振型。将式(3)代入式(1)得:

上式左乘以{φs}T，并考虑到:

其中，cs为模态阻尼系数。于是上式变为:

令 f(t)={F}ejωt，则 qs=Qsejωt，代入上式得:

可以看出Qs相当于一个质量、刚度和阻尼分别为ms，ks，cs的单自由度系统在模态力 Ps={φs}T{F}作用下的响应。

根据式(3)，不考虑初始条件，可得位移响应为:

其中:

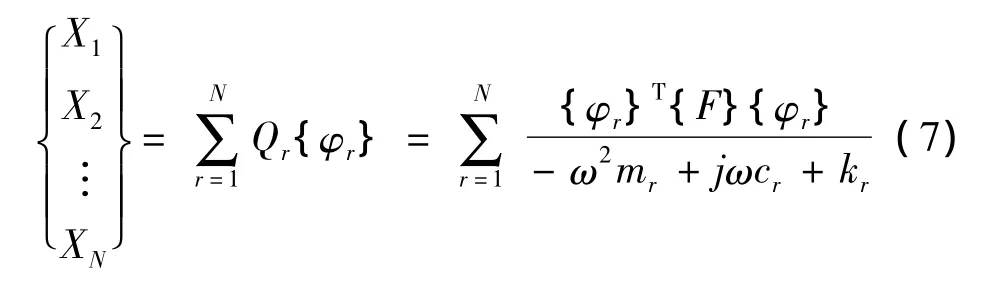
式(7)即为具有比例阻尼的系统进行响应计算的模态模型。

在模态分析中假定系统是线性的。线性假设即结构系统对任一组同时作用激励的响应是该组内每一激励单独作用时系统响应的线性叠加。对于一个N个自由度的线性系统，其位移响应可以看成各阶模态响应的线性叠加，那么其传递函数同样是展成N个单自由度系统的传递函数线性叠加，即:

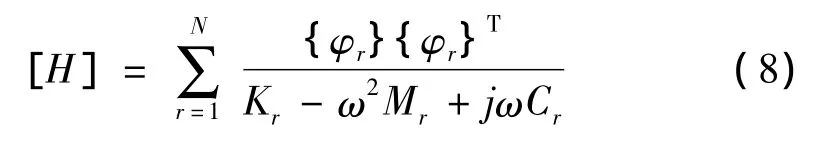
其中:Kr，Mr，Cr，φr分别为模态刚度、模态质量、模态阻尼和模态振型。从式(8)抽取任意一行和一列为:

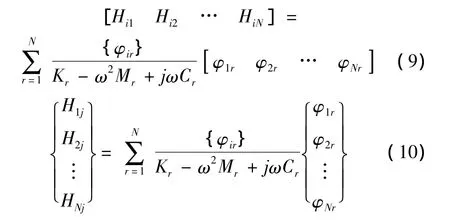
从式 (9)和式 (10)可见，位移传递函数矩阵［H］是对称的，它的任一行或任一列均包含所有模态参数信息，那么通过这一点可以知道:如果在结构上的某一固定点第i点拾振，而轮流地激励所有的点，即可求得传递函数矩阵的一行;如果在某一固定点第j点激振、而在其他各点拾振，即可求得传递函数矩阵的一列。两种方法均可用来获取传递函数［7］。所以采用SISO方法测结构模态时，采用激励点不动移动拾振点，或者拾振点不动移动激励点都能得到完全一样的传函数。

2 组合系统的频响特性的分析

以一个具有两部件的系统为例说明问题。为求图1所示的系统在F1作用下产生在1点的位移X1，先将系统分为Ⅰ和Ⅱ。连接点为2点，该点的位移为X2。

取分离体后，连接处的作用分别以力F2Ⅰ及F2Ⅱ来代替。对于部件Ⅰ，可得:

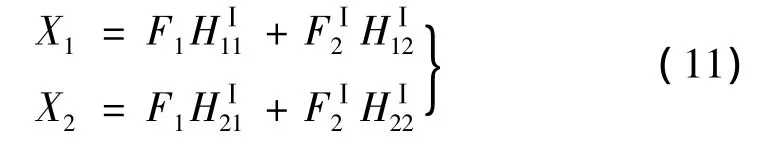
对于部件Ⅱ，可得:

在连接点，若以位移的方向为参考方向，则有:

于是由式 (11)，式 (12)，式 (13)可得:

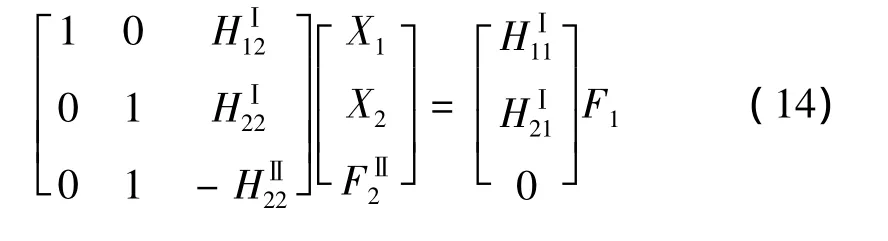
式(14)有三个方程，求解三个未知数，因此有唯一解。以上即由部件的动态特性求总体结构动态特性的理论依据。

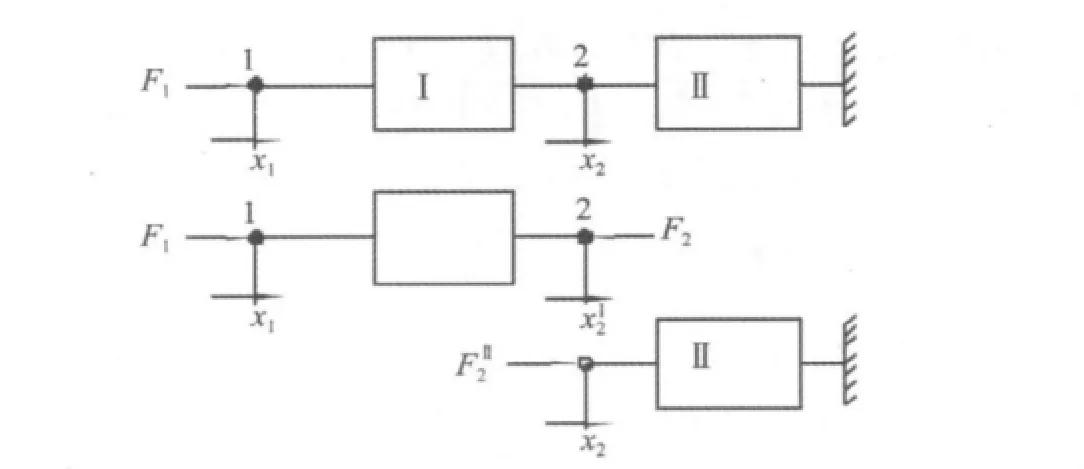
图1 两部件系统Fig.1 Two-part system

3 模型试验

3.1 渡槽模型

本次试验的模型，下部采用四根钢管桩;承台、槽墩及槽体均为钢筋混凝土材料。基本构成见图2，其具体尺寸见图3。

3.2 实验模型建立

为了便于模态的测试，本实验进行了两项实验，上部结构试验以及桩实验。系统整体使用笛卡尔全局坐标系。由于结构的对称性，各桩的模态存在轴对称或者点对称的关系。因此在桩的实验中对一根桩进行了测试，以减小的难度和工作量。其测点布置分别见图4、图5。为了使实验结果更加贴近实际，并与计算结果相比较，建立桩－槽体模型，见图6。

图4 桩测点布置Fig.4 The sensor arrangement of the pile-pier

3.3 实验系统及实验装置

实验模态分析是在实验室内通过人为或者环境对结构施加一定动态激励，并采集各点的振动响应信号及激振力信号，根据力及响应信号用各种参数识别方法获取模态参数。图7为实验系统原理图，激励方法不同，响应识别方法也不同。目前主要有单输入单输出(SISO)、单输入多输出 (SIMO)、多输入多输出(MIMO)三种方法。以输入力的信号特征还可以分为正弦慢扫描、正弦快扫描、稳态随机 (包括白噪声、宽带噪声或伪随机)、瞬态激励 (包括随机脉冲激励)等。本实验采用SISO方法进行实验:对桩的实验采用的是激励点不变响应点移动;而对上部结构的实验则是采用响应点不动激励点移动的方法。由式(9)、式(10)知，此两种方法能得到一样的传函数。

本实验的难点在于对桩模态的测定，由于桩是采用重锤打入土中的，在桩打入土之前并没有布置加速度传感器。采用SIMO方法测模态时，如何把加速度计准确的布置于侧点上是一个很大的难题。因此我们自己自制了一个小装置，将加速度计嵌入到两端都有磁铁的磁座内，磁铁会自动吸附在钢管内壁。通过一个电磁铁控制磁性的方向与强弱来实现加速度计布置到不同的测点上。图8为装置图。其工作原理见图9。

测得数据以后采用峰值法 (PP)估计频率，峰值法最初是基于结构自振频率在其频率响应函数上会出现峰值，峰值的出现可以作为特征频率的良好估计。它具有处理简单、快速、实用等特点，然而，其不足之处在于峰值的选取比较主观，难以得到比较准确的振型，仅适用于比例阻尼和实模态结构［8］。本文分析中尽量采取平均技术［9］处理试验数据，最大程度地消除了这种影响。模态测试以过程由武汉优泰电子技术有限公司生产的UT3308动态测试系统完成;模态参数的分析及识别由优泰结构与机械模态分析软件完成。模态拟合方法为频域法中的实模态多自由度整体拟合方法。

图8 测点布置及装置图Fig.8 The device of measuring points

图9 装置工作原理图Fig.9 Working principle of the device

3.4 实验结果

由于实验是分桩和上部结构两部分进行的，而且只对其中一根桩进行了实验，而实际上桩与槽墩是一个整体。由于模态实验时桩与槽墩所选择的参考点不同，若统一两模态，需利用到模态合成技术即子结构技术［10－11］，将桩及槽墩的模态进行组合得到整体模型模态。再根据桩的对称性，以及变形协调条件，把单根桩的模态振型系数统一乘以系数k。具体来说，由变形协调条件，由于桩的上端与槽墩下部是相连的，所以他们之间没有相对位移。所以乘以系数k之后使之满足变形协调条件，而得到桩－槽墩体系的整体阵型。处理后结果见图10。其中Z向与X向的规定见图6。

由于参考点的不同，以及模态试验时采用的放大倍数不同，所以调整系数会不一样。由表1可以看出，槽墩的平动模态都是乘了一个正数，这是因为对于平动模态激励与响应的方向始终是一致的;槽墩上下错动模态中所有的调整系数都是负数，这是因为此阶模态对槽墩上部进行激励时，下部的响应方向与激励方向是相反的;槽墩扭转时桩①、桩②是正数，而桩③、桩④是负数，是因为槽墩在扭转模态时，对槽墩一侧进行激励时，另外一侧响应始终与激励这侧方向相反。

由上述分析可以看出，调整系数不仅满足变形的协调条件，同时也满足结构固有的频响特性。

表1 调整系数kTab.1 The coefficient k

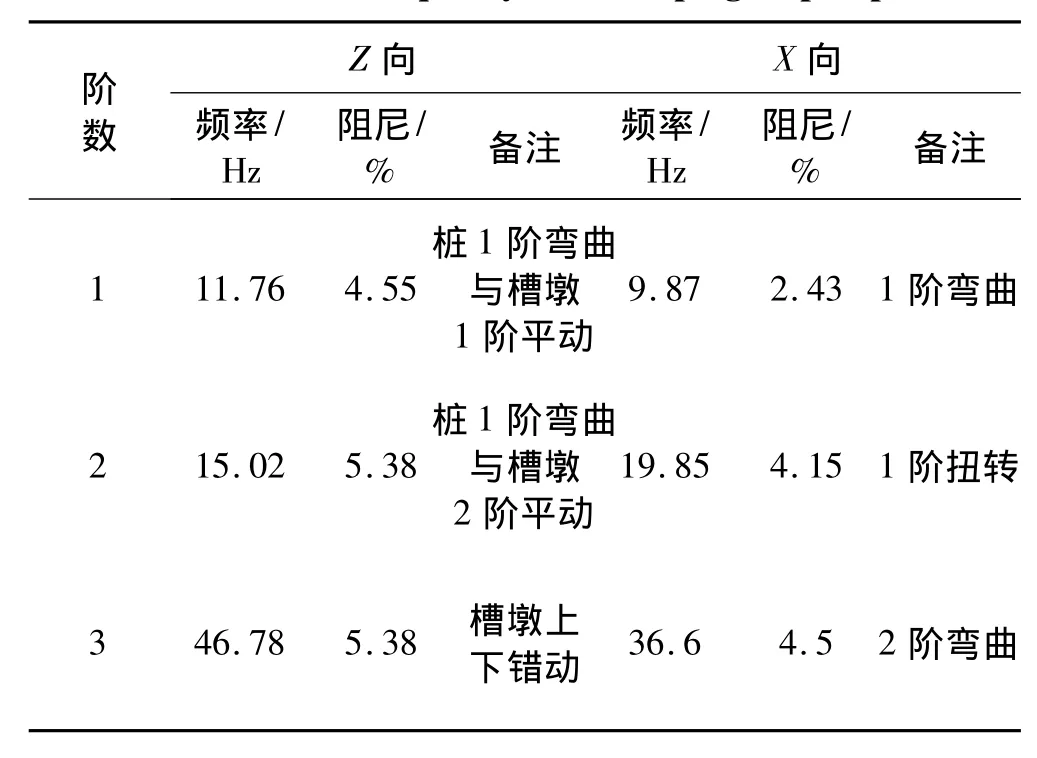
表2 桩与槽墩的自振频率及阻尼Tab.2 Natural frequency and damping of pile-pier

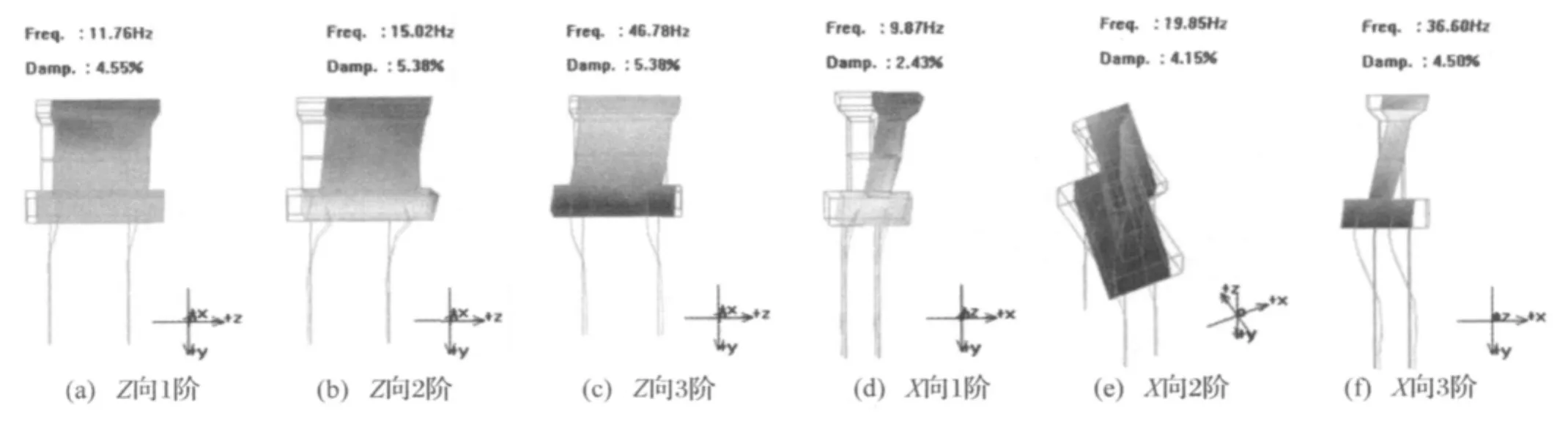
图10 桩－槽墩模态图Fig.10 Mode of Pile-pier

从实验结果可以看出，由于模态实验是分X和Y两个方向进行的，所以所得到的模态只是所测方向上的分量。

4 有限元计算

4.1 计算参数

上部结构的混凝土强度为 C30，密度为2 500 kg/m3，弹性模量 30 GPa，泊松比 0.2;钢管桩密度为7 850 kg/m3，弹性模量 210 GPa，泊松比 0.25;土的参数由实验确定，密度为1 980 kg/m3，弹性模量215 MPa。

4.2 计算模型

本模型采用大型通用有限元软件ABQUS建立。其中土与上部槽墩均采用均质实体单元，钢管桩采用壳体单元。为了简化计算，土与桩采用绑定约束，由于模态测试为微小变形，认为桩与土是一起运动的，所以使用这种简化有其合理性。土体边界根据现有理论，可以采用人工边界，本文土体截取边界尽量接近实际情况，采用了刘晶波等［12］的黏－弹性人工边界。模型上部结构单元数为1 650，土体单元数为76 050，每根桩的单元数为2 973，总单元数为89 592。除桩为四边形壳体单元外，其他部件均为六面体实体单元。采用线性摄动分析步进行频率的计算，并用Lanczos求解器求解其特征值。其模型见图11。另外为了与刚性地基进行比较，本文还抽取了上部结构，固定其底座，计算其自振频率以及振型。其模型见图12。

4.3 计算结果

通过有限元计算得到以下结果，表3与表4分别给出了Z向、X向两个方向计算值与实验值及其计算值的误差。表5为刚性地基模型计算结果。

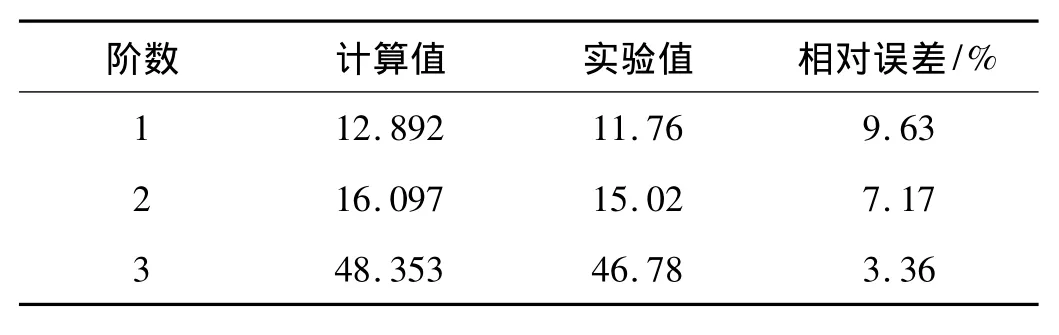
表3 桩－土模型Z向结果Tab.3 The results of pile-soil model in Z direction

表4 桩－土模型X向结果Tab.4 The results of pile-soil model in X direction

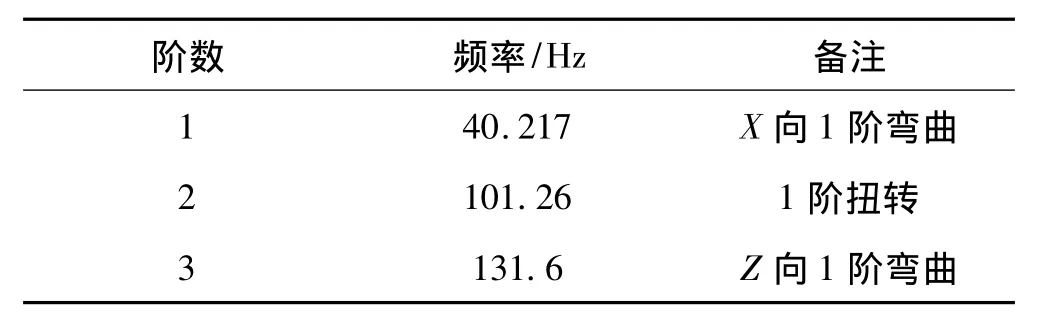
表5 刚性地基计算结果Tab.5 The results of the rigid foundation model

表3、表4中的相对误差为实验值减去计算值再除以实验值，由这两个表可以看出计算结果最大误差为12.28%，说明有限元简化模拟正确可行。

为了方便与实验对应，在显示中移除了土，模型计算结果只提取了桩和槽墩的模态。其频率与试验结果相近而且振型相同的为同一阶模态，其具体振型见图13。需要说明的是，在模态实验的过程中是分了Z向和X向两个方向进行的。而在有限元计算过程中，则是三维立体的，所以第一阶扭转，在模态实验中是Z向和X向两个方向各自都有一阶与其对应实验过程中X向的扭转较为明显，所以只列出了X向扭转模态。

把桩－土有限元模型与表5刚性地基有限元模型的计算结果进行对比，从频率来看刚性地基模型的自振频率要明显高于桩－土模型的频率，这与文献［13］所得到的结果完全一致;从其振型来看，桩－土模型其振型基本上是由桩决定，槽墩可看作是刚性的，而刚性地基模型则是槽墩自身的振动。刚性地基振型见图14。

5 结论

通过以上的分析，可得到以下结论:

(1)本文采用自制的装置，对打入实际土层的钢管桩进行横向位移模态实验，揭示了桩－土－上部结构相互作用的振动特性，对渡槽的抗震研究有一定的参考价值。

(2)本文实验对桩的模态实验采用了模型的对称性，并应用现有子结构理论合成了桩－槽墩的整体振型，降低了实验难度及实验工作量。

(3)通过实验结果与计算结果的比较，实验模态是某个方向的振动形式，而计算模态则是立体振型。所以计算模态从形式上补充了实验模态。从实验频率与计算频率比较来看，计算结果最大误差为12.28%，说明了有限元模拟是合理的。计算结果要比实验结果偏大，这是因为计算时土对桩的约束比实测时要强。

(4)通过与刚性地基计算结果的比较，桩－土－上部结构模型能很好的延长结构的自振周期，降低自振频率。

［1］ 王 博，李 杰.大型渡槽结构模态分析［J］.地震工程与工程振动，2000，20(3):60－66.

［2］ 李正农，孟吉复.多槽体渡槽的自振特性分析［J］.武汉大学学报 (工学版)，2001，34(4):11－16.

［3］ 赵伟封.桩－土动力体系的模型试验及动力特性计算［J］.西安公路学院学报，1993，13(2):23－30.

［4］ 周 云，易伟建.考虑土－结构动力相互作用的框架结构的参数识别研究［J］.土木工程学报，2007，40(6):14－19.

［5］ 王 博，徐建国.大型渡槽考虑土－结构相互作用的动力分析［J］.世界地震工程，2000，16(3):110－115.

［6］ 杨世浩，李正农，郑明艳.南水北调工程洺河渡槽耦合动力分析［J］.湖南大学学报(自然科学版)，2007，34(12):15－19.

［7］ 李德葆，陆秋海.实验模态分析及应用［M］.北京:科学出版社，2001.

［8］ 戴恩彬，任伟新.湛江海湾大桥环境振动实验与模态分析［J］.中国水运，2009，9(11):167－169.

［9］ 张爱林，王冬梅，刘学春，等.2008奥运会羽毛球馆弦支穹顶结构模型动力特性试验及理论分析［J］.建筑结构学报，2007，28(6):68－75.

［10］ BouhaddiN， Lombard J P. Improved free-interface substructures representation method［J］.Computers and Structures，2000，77:269－283.

［11］ Kim D K，Lee M S，Han J H.Substructure synthesis method for a nonlinear structure with a sliding mode condition［J］.Journal of Sound and Vibration，2009，321:704－720.

［12］ 刘晶波，王振宇，杜修力，等.波动问题中的三维时域粘弹性人工边界［J］.工程力学，2005，22(6):46－51.

［13］ 李正农，张盼盼，朱旭鹏，等.考虑桩－土动力相互作用的渡槽结构水平地震响应分析［J］.土木工程学报，2010，43(12):137－143.