一种基于非线性流形学习的故障特征提取模型

蒋全胜，李华荣，黄 鹏

(1.巢湖学院 电子工程与电气自动化学院，巢湖 238000;2.东南大学 机械工程学院，南京 211189)

目前，大型机械设备的结构与工作状况的复杂性及其非线性特性日益突出，设备运行监测数据蕴含了机械设备在整个运行历程中的所有信息，如何从这些数据中提取有效特征信息，判定设备的运行状态并对所发生的故障进行准确诊断，对于现有的故障诊断方法提出了新的考验[1]。

特征提取是机械故障诊断的核心问题，也是进行故障模式识别的基础。如何选择和提取最有效的故障特征，不仅可以节省测试成本，还直接影响故障诊断的精度。随着现代信号处理方法的不断发展，一些新的特征提取方法相继被提出。魏中青等[2]采用基于MLE阈值规则的小波特征提取技术对气阀早期故障弱冲击变化信号进行特征提取，实现了气阀故障的早期预警。夏天等[3]对柴油发动机曲轴轴承采用基于高阶累积量的故障特征提取方法，能够有效地抑制噪声的干扰，较好地反映曲轴轴承的技术状态。潘宏侠等[4]针对齿轮传动箱故障特征选择问题，提出了基于粒子群优化算法的特征提取方法，进一步提高了诊断精度。栗茂林等[5]采用局部切空间排列算法对最优小波系数矩阵进行非线性约简，提出了一种基于连续小波系数非线性流形学习的冲击故障特征提取方法，有效提取出机械设备故障引发的冲击成分。

当前，虽然故障诊断理论和方法的研究取得了较大的进步，但对于不确定的、非线性的复杂故障诊断问题，采用基于统计或信号处理的特征提取方法，其诊断效果十分有限[1]。2000年在Science上发表的三篇关于流形学习的研究成果[6－8]，极大地推动了流形学习的发展。流形学习作为一种非线性的数据维数约简方法，能有效地揭示高维数据中蕴含的非线性结构，充分挖掘数据中的内在几何特征，具有良好的非线性复杂信息处理能力，从而为复杂机械设备的故障特征提取提供了新的思路。

本文采用非线性流形学习方法进行机械故障特征的提取与诊断，通过构建基于流形学习的故障特征提取模型，准确提取故障数据内在的非线性结构信息，以提高故障诊断的精度。

1 流形学习原理及方法

1.1 流形学习定义

流形是现代数学的概念，它以微分几何学为基础，本质上是局部可坐标化的拓扑空间，可以看作是欧氏空间的非线性推广。流形学习的数学描述如下[9]:

假设M为嵌入在D维欧氏空间中的d维参数化流形，d≪D，f∶M⊂Rd→RD，M 为 Rd上的紧致连接开子集。对于给定的高维观测数据集X={x1，x2，…，xn}，i=1，2，…，n，其中 Xi=f(yi)⊂RD，服从某种潜在分布p。这里，Y={y1，y2，…，yn}⊂Rd是包含在 Rd欧式空间的d维域。流形学习的任务即从观测数据集中重构映射 f和 Y。

由流形学习的定义可知，流形学习去除了更多的先验假设，比如观测变量之间相互独立、分布近似满足正态分布等，是一种一般意义上数据集的本质属性。流形学习具有在不依赖这些先验假设的情况下，发现并学习高维数据集的内在规律与性质的能力，这为故障特征提取提供了一个新的思路。

1.2 流形学习算法

典型的流形学习方法有局部线性嵌入算法(Local Linear Embedding，LLE)[7]、等距映射算法(Isometric Mapping，ISOMAP)[8]、拉普拉斯特征映射算法(Laplacian Eigenmaps)[10]、局部切空间排列算法(Local Tangent Space Alignment，LTSA)[11]等。 其 中 Laplacian Eigenmaps算法的基本思想是利用图拉普拉斯算子的谱性质进行求解，寻找在某种意义上最优地保持局部邻域信息的低维表述。

Laplacian Eigenmaps作为一种典型的流形学习方法，以保持局部几何结构信息不变为目标，能挖掘嵌入在高维故障数据中的内在几何分布特性，具有良好的学习非线性复杂数据的内在几何结构能力，可用于故障的特征学习和提取。Laplacian Eigenmaps算法具体步骤如下[10]:

(1)构造近邻图。给定邻域k，用k近邻或ε邻域的方法计算每个样本点xi的邻域Γ(i)，1≤i≤n。

(2)使用热核方式给每条边赋予权值Wij，构建邻接权值矩阵W;

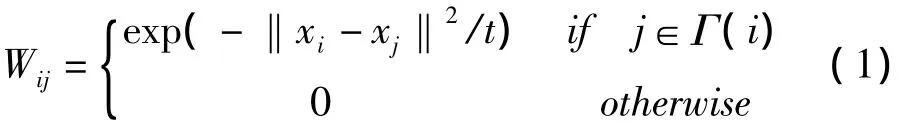
其中参数t为热核宽度，其取值与邻域k相适应。

(3)特征映射，计算图拉普拉斯算子的广义特征向量，求得低维嵌入。求解广义特征值问题，Lf=λDf。其中D为对角矩阵，且Dii=ΣjWji，得到L的第2个到第d+1个特征值对应的特征向量，即为样本集的低维嵌入坐标。

图1 基于流形学习的故障特征提取模型Fig.1 Fault feature extraction model based on manifold learning

2 基于流形学习的故障特征提取模型

在机械故障诊断过程中，特征提取是其中最重要而又最困难的环节，好的特征提取手段能够给出设备运行状态的准确描述，获得更好的故障诊断精度和速度。因此，寻求合适的特征提取方法成为提高机械故障诊断精度的关键。

本文基于流形学习方法，提出一种新的机械故障特征提取模型，该模型利用流形学习的非线性结构学习能力，对故障样本进行特征提取，将提取到的的低维流形特征作为分类特征，用于解决复杂机械系统的故障模式识别问题。所构建的基于流形学习的故障特征提取模型如图1所示。

与传统的故障特征提取方式不同，该模型充分利用了流形学习挖掘数据非线性特性的优势，从故障样本的内在几何分布角度进行故障的特征提取和识别，可有效解决高度非线性、非结构化、高维度样本的故障诊断问题，为解决复杂的故障诊断问题提供了一条新的途径。

在基于流形学习的故障特征提取模型中，重点关注于如何获取有效的特征信息，解决故障分类问题。该模型主要针对以下三种不同的应用场合:无标签故障样本的特征提取问题、故障样本不断更新情况下的特征提取问题以及含有标签故障数据的监督学习问题，采用不同的流形学习方法，进行故障样本的特征提取和模式分类。

2.1 基于Laplacian Eigenmaps的特征提取

针对采集到的无标签故障样本的特征提取问题，采用基于Laplacian Eigenmaps的特征提取方法，获得故障样本的低维几何分布特征，以利于故障分类和识别。基于Laplacian Eigenmaps算法的故障特征提取过程包含以下步骤:

(1)将监测设备采集到的各种模式样本数据经信号预处理得到原始观测样本集，构成观测样本的模式空间;

(2)用Laplacian Eigenmaps算法对观测样本进行学习，获取其内在的几何分布特征，从而将样本从复杂高维的模式空间转化为低维的特征空间;

(3)根据学习到的故障流形特征，将特征空间样本进行模式分类构成类别空间，并构造分类器;

(4)对于未知故障样本，与原样本一同投影到故障类别空间，依据构造的分类器进行类别判别及分类。

Laplacian Eigenmaps算法从数据集的几何性质出发，能够挖掘数据的内在结构信息及其蕴含的整体几何特征，可以将提取到的流形特征应用于机械的故障特征识别，为故障分类提供客观依据。

2.2 基于增量Laplacian Eigenmaps的特征提取

针对故障样本不断更新情况下的特征提取问题，采用增量流形学习方法，以提高流形特征提取的自学习能力。

一般流形学习算法采用批处理方法学习样本特征，不具有增量处理能力，需要解决增量流形学习问题。本文采用增量Laplacian Eigenmaps算法进行故障样本的特征提取。增量Laplacian Eigenmaps算法的实现步骤如下:

(1)首先用Laplacian Eigenmaps算法对原始样本集X进行学习，得到对应的低维嵌入坐标Y。

(2)对于任一新增样本xN+1，XN+1∈XNew，在原始样本中寻找xN+1的k个近邻点。其近邻点在低维空间相应的邻域为

(3)假定邻域内每个样本的映射关系不变，计算xN+1与其k个近邻点间的权值矩阵W，采用如下热核形式计算:

(4)对新增样本xN+1，保持其邻域局部映射关系不变，可计算其在低维空间的坐标yN+1为:

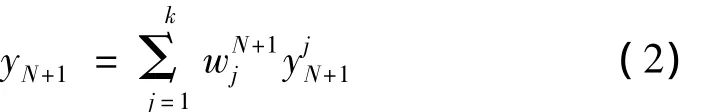
该算法较好的保持了新增样本的邻域局部映射关系，以邻域内样本的权值矩阵求得新样本对应低维空间的位置坐标。当数据集实时更新的情况下，可保证提取的特征信息能够随新数据的增加而动态更新，从而有利于更新故障样本的诊断分析。

2.3 基于监督Laplacian Eigenmaps的特征提取

如果采集到的故障样本是有标签的，可以充分利用样本的类别标签信息，进行基于监督流形学习的特征提取，进一步提高分类性能。故可对 Laplacian Eigenmaps算法进行监督式扩展，采用监督Laplacian Eigenmaps算法完成有标签故障样本的特征提取和故障分类。

采用的监督Laplacian Eigenmaps算法描述见文献[12]，该算法充分利用数据的局部几何信息和类别信息，将原始故障样本映射到新的特征空间，该空间在保持类内样本局部几何结构的同时，使得不同类样本在映射后的特征空间中具有可分离性，从而更有利于不同故障模式的分类处理。

阿里又使劲点点头。阿东又说：“罗爹爹去东湖练拳，走不动了。我们阿里每天早上用爸爸的轮椅推罗爹爹去，好不好？”

基于监督Laplacian Eigenmaps算法的特征分类方法实现如下:首先采用监督Laplacian Eigenmaps算法将训练样本集映射至一个低维特征空间，并采用最近邻分类器构建故障分类器，再用GRNN网络对训练集的低维映射过程进行估计，以获得未知测试样本的低维坐标，从而实现对测试样本的分类决策。监督流形学习算法充分利用了数据的类别信息，能提取有效的判别特征，获得更好的分类性能。

3 工程应用实例分析

选取某公司动力厂现场运行的一离心空气压缩机组作为实例应用对象。该对象是一个多因素、强耦合、强非线性和难以建模的复杂系统。从运行的压缩机组采集到故障振动信号作为样本实例集，包含了三种类别故障:机械松动、油膜涡动及转子不平衡。数据集样本总数N=210，每类故障样本各70个，以1 024个采样点作为样本维数。数据集的点数少，维数高，呈现了较强的非线性特征。

3.1 应用实验

通过建立的故障特征提取模型进行了如下三种情形的实验分析和应用:

(1)无监督特征学习情况:分别用PCA及Laplacian Eigenmap算法对数据集进行特征提取，获取嵌入流形特征以进行模式识别分析。设定算法参数邻域因子k=6，嵌入维数d=2。实验结果如图2所示。

(2)样本不断更新情况下的增量式学习情况:采用增量Laplacian Eigenmaps算法对实例集进行特征提取和故障分类，将实例集的210个样本点分成两个子集，随机选取各类的80%作为原始数据集进行训练，剩下的20%作为新增样本集进行测试。算法参数设定为:邻域因子k=6，嵌入维数d=2。实验结果如图3所示。

(3)有标签故障样本的监督特征学习情况:采用监督Laplacian Eigenmaps、PCA及LDA方法对实例集进行特征提取和分类，随机选取各类的80%作为有标签训练集进行学习，剩下的20%作为测试集进行识别分类。算法参数设定为:邻域因子k=10，嵌入维数d=2。实验结果如图4所示。

图2 流形特征提取情况Fig.2 Feature extraction using manifold method

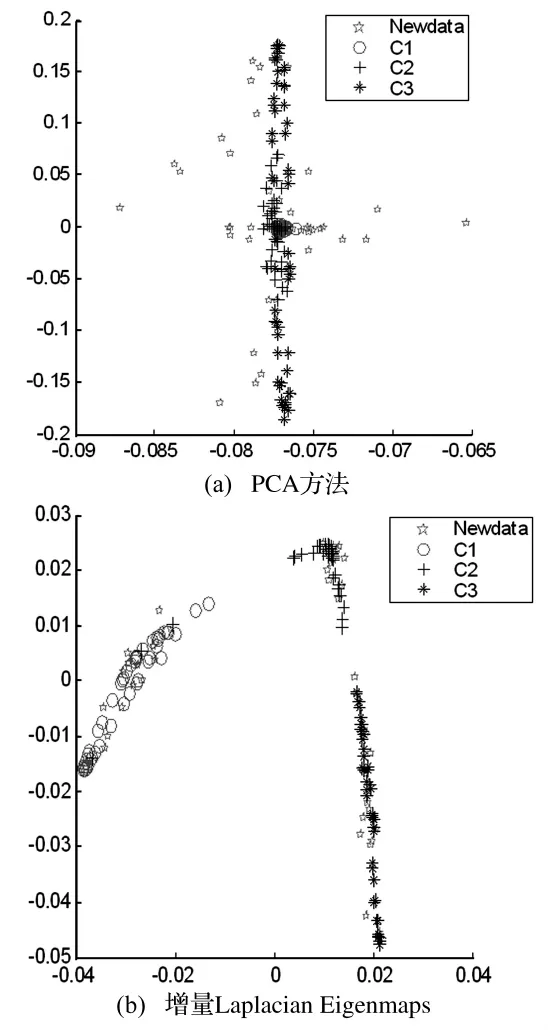
图3 增量流形特征提取情况Fig.3 Feature extraction using incremental manifold method

3.2 诊断结果

对原始故障样本经过三种不同应用场合的流形特征提取，将各方法特征提取后的特征样本均采用最近邻分类器进行故障分类，结果如表1所示。

图4 监督流形特征提取情况Fig.4 Feature extraction using supervision manifold method

在图3提取的2维特征分布中，PCA提取到的2维分布特征中三类样本有较大混叠，用最近邻分类器分类的正确率为51.36%;增量Laplacian Eigenmaps算法提取的特征类别可分性较好，其中仅有少量样本被错分，其分类正确率为90.58%，在新增样本情形下也表现出良好的分类性能。

从图4和表1可以看出，PCA和LDA中有三类样本存在较大混叠，其类别可分性较差，各分类正确率分别为 59.92%、71.55%;而监督 Laplacian Eigenmaps算法的类别可分性得到明显改善，其分类正确率达到98.62%，表现出更佳的分类能力。

表1 用最近邻分类器对各特征提取算法的分类正确率Tab.1 Classification accuracy of feature extractionmethods using nearest neighbor classifier

通过前面的实验可以看出，采用基于Laplacian Eigenmaps、增量 Laplacian Eigenmaps和监督 Laplacian Eigenmaps三种流形学习算法的故障特征提取方法，通过对高维故障样本进行学习，能够较好的获取数据内在的整体几何结构信息，对获取的结构特征易于进行故障分类器的构造与模式识别，表现出了较好的分类性能，实现了故障分类识别与诊断，其识别效果明显好于PCA方法。

基于流形学习的故障特征提取模型在处理高维复杂故障样本时，经流形学习算法特征提取之后，极大地保存了原始的整体几何特征信息，更有效地反映出特征与故障之间的关系，使得故障诊断精度高于其它方法，实验证明是一种有效的故障特征提取方法。

4 结论

针对机械故障诊断中高维度、非线性数据难以有效处理的问题，将流形学习方法应用于故障样本的特征提取，提出了一种基于非线性流形学习的故障特征提取模型。该模型针对三种不同的应用场合，分别采用不同的流形学习方法，对于不断更新的故障样本采用增量算法，对于有标签故障样本采用监督算法，进行故障样本的特征提取和分类，具有良好的学习非线性数据内在几何结构能力。将该模型应用于空气压缩机故障振动信号的诊断分析，能够有效地进行故障信号的特征提取和诊断，提高了故障诊断的有效性和诊断精度。

在应用的三种流形特征提取方法中，其提取特征的效果一定程度上受到邻域因子和嵌入维数等参数选取的影响，如何选取合适的算法参数，将是下一步研究工作的重点。

[1]钟秉林，黄 仁，贾民平，等.机械故障诊断学(第3版)[M].北京:机械工业出版社，2007.

[2]魏中青，马 波，窦 远，等.基于MLE阈值规则的小波特征提取技术在气阀故障诊断中的应用[J].振动与冲击，2011，30(1):237 －241.WEI Zhong-qing，MA Bo，DOU Yuan，et al.Wavelet feature extracting technique based on maximum likelihood estimation threshold rule and its application in fault diagnosis of a gas valve[J].Journal of Vibration and Shock，2011，30(1):237－241.

[3]夏 天，王新晴，赵慧敏，等.基于高阶累积量的柴油发动机曲轴轴承故障特征提取[J].振动与冲击，2011，30(1):77－81.XIA Tian，WANG Xin-qing， ZHAO Hui-min， etal.Extracting fault features of a Diesel engine s crankshaft bearing based on high-order cumulation[J].Journal of Vibration and Shock，2011，30(1):77－81.

[4]潘宏侠，黄晋英，毛鸿伟，等.基于粒子群优化的故障特征提取技术研究[J].振动与冲击，2008，27(10):144－147.PAN Hong-xia，HUANG Jin-ying，MAO Hong-wei，et al.Fault-characteristic extracting technology based on particle swarm optimization[J].Journal of Vibration and Shock，2008，27(10):144－147.

[5]栗茂林，梁 霖，王孙安，等.基于连续小波系数非线性流形学习的冲击特征提取方法[J].振动与冲击，2012，31(1):106－111.LI Mao-lin，LIANG Lin，WANG Sun-an，et al.Mechanical impact feature extraction method based on nonlinear manifold learning of continuous wavelet coefficients[J].Journal of Vibration and Shock，2012，31(1):106 －111.

[6]Seung H S，Daniel D L.The manifold ways of perception[J].Science，2000(12):2268 －2269.

[7]Roweis S，Saul L.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290(5500):2323－2326.

[8]Tenenbaum J B，de Silva V，Langford J C.A global geometric framework for nonlinear dimensionality reduction[J].Science，2000，290:2319 －2323.

[9]Silva V D，Tenenbaum J B.Global versus local methods in nonlinear dimensionality reduction[J].In:Advances in Neural Information Processing Systems，2003:705 －712.

[10]Belkin M，Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation，2003，15(6):1373－1396.

[11]Zhang Z Y，Zha H Y.Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J].Journal of Scientific Computing，2005，26(1):313－318.

[12]Jiang Q S，Jia M P，Hu J Z，et al.Machinery fault diagnosis using supervised manifold learning[J].Mechanical Systems and Signal Processing，2009，23(7):2301－2311.