基于电流补偿的汽车制动特性试验技术仿真研究

蔺小林，王玉梅

(陕西科技大学电气与信息工程学院，陕西西安710021)

0 引言

随着汽车产业的竞争越来越激烈，人们对汽车制动性能要求越来越高［1］.汽车制动器的性能优劣直接关系到车辆和人身的安全，为了检测制动器的综合性能，需要在各种不同情况下进行大量路试.但是，车辆设计阶段无法路试，只能在专门的制动器试验台上对所设计的路试进行模拟试验.因此，台架试验台被用来模拟实车制动，它的制动过程与路试时的制动过程要求尽可能一致［2-3］.

传统的惯性台架中有一组惯性质量飞轮组进行机械模拟，虽然可以比较充分和准确地再现制动机构的工作状况，但是存在着体积和质量大、模拟误差较大等缺点，其成本高且不能适应路面的变化，因此难以大量实际应用［4-5］.

笔者采用机械惯量电模拟技术，利用驱动电流对制动过程中由于机械惯量不足而缺少的能量进行补偿，能够提高试验台与路试的仿真程度，克服单纯依靠飞轮惯量的缺点.并用能量误差作为评价标准，以验证该惯性台架的可行性.

笔者所阐述的制动器试验台驱动电流控制方法，对制动器试验台产生积极的影响，缩小了试验台的体积，减轻其重量，而且模拟性能好，自动化程度高，能够较好完成汽车制动控制系统的要求.为进行制动器的基础研究和性能测试提供有效的技术手段.而且该控制方法可应用于各种车辆制动性能的测试，对深入开展汽车制动控制系统研究，降低事故发生率，减少人员财产损失，促进智能交通的发展具有重要意义［6］.同时也可运用于生物医药工程，如化工生产中对于各个参数的反馈控制，造纸过程中时刻监控系统压力，温度，流量等参数.

1 制动器试验台原理

制动器试验台一般由安装了飞轮组的主轴、驱动主轴旋转的电动机、底座、施加制动的辅助装置以及测量和控制系统等组成.被试验的制动器安装在主轴的一端，当制动器工作时会使主轴减速.试验台工作时，电动机拖动主轴和飞轮旋转，达到与设定的车速相当的转速后电动机断电同时施加制动，当满足设定的结束条件时就称为完成一次制动［7-8］.其结构如图1所示.

图1 试验台结构示意图Fig.1 Test rig structure schematic drawing

为了评价制动系统的优劣，笔者在分析了能量误差的基础上，建立了驱动电流控制模型，通过增大驱动电流来不断补偿能量误差，减小偏离，使得实际模拟转速与理想转速逼近，以提高试验台和路试的仿真程度.

2 制动特性模型建立

2.1 模型假设

由于制动器性能的复杂性，电动机驱动电流与时间之间的精确关系很难得到，笔者建立了期望制动车辆车轮数学模型.在试验台上，载荷是用飞轮组成来模拟的，然而飞轮的转动惯量是离散的，只能模拟有限的几个转动惯量.因此，在模拟任意数值的等效惯量时，需要利用电流补偿飞轮组转动惯量的不足，所以要用到驱动电流控制的方法.通过对制动系统的转速和制动距离进行优化，使得模拟值与实际值逼近.基于MATLAB软件环境进行仿真，通过能量误差以评价所设计算法的优越性.假设:

(1)路试时轮胎与地面的摩擦力为无穷大，故轮胎与地面无滑动，踏下制动踏板的力是恒定的;

(2)把载荷在车辆平动时具有的能量等效地转化为试验台上飞轮和主轴等机构转动时具有的能量时，忽略车轮自身转动具有的能量;

(3)试验台采用的电动机的驱动电流与其产生的扭矩成正比，且试验台工作时主轴的瞬时转速与瞬时扭矩是可观测的离散量;

(4)路试时轮胎与地面的摩擦力为无穷大，主轴的角速度与车轮的角速度应尽量一致，飞轮，3个飞轮的惯量分别为 30，60，120 kg·m2，它们和基础惯量一起组成的机械惯量可以有8 种情况:10，40，70，100，130，160，190，220 kg·m2.

2.2 模型求解

(1)设前轮的半径为R，制动时承受的载荷为G，等效的转动惯量为J，线速度为v，角速度为ω，重力加速度为g.由能量法得到:

(2)设飞轮厚度为h，密度为ρ，内半径为R0，外半径为R1，则飞轮惯量

则计算得到3个飞轮的惯量分别为30，60，120 kg·m2.因为械惯量有23种，记为J1，则J1=10，40，70，100，130，160，190，220 kg ·m2，由 J=J1+

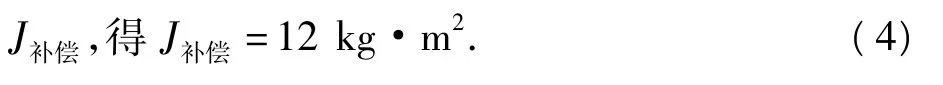
当J1取40 kg·m2时，因为此时J补偿绝对值最小，模拟效果最好.

2.3 模型仿真及分析

设主轴转速为ω(t)，则J关于主轴制动力矩为

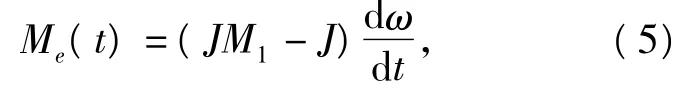
故电机的驱动电流为

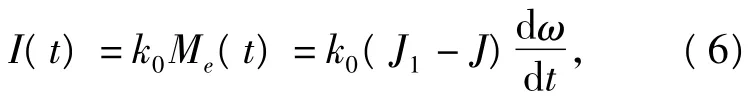
式中:比例系数取为k0=1.5 A/(N·m).

记初速度为v0，末速度为v1，车轮的滚动半径为R，制动时间为T，则

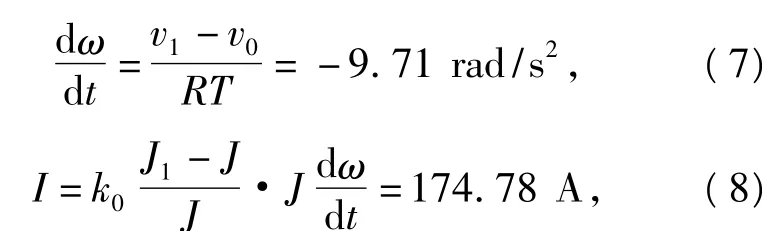
将时间离散化:把整个刹车过程等分为N个时间段，记 tk=kΔt，Δt为时间步长，第 k个时间段为［tk-1，tk］.设 tk时的角速度为 ωk，制动扭矩为Mk，等效的转动惯量为J，初始角速度为ω0.则拟合出时间与转速关系如图2所示.

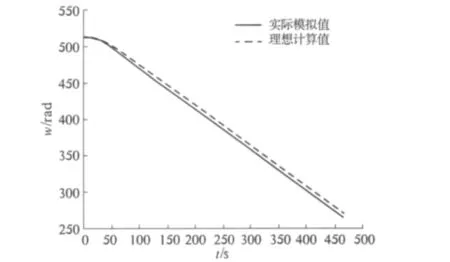
图2 改进前转速与时间的关系图Fig.2 Speed and time relationship chart before improvement

由图2可以看出:理论上能量应该减少

而实际上能量减少为

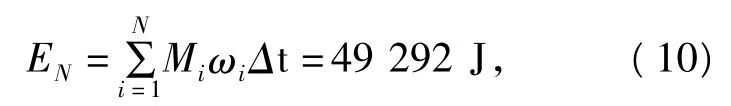
于是，相对误差定义为

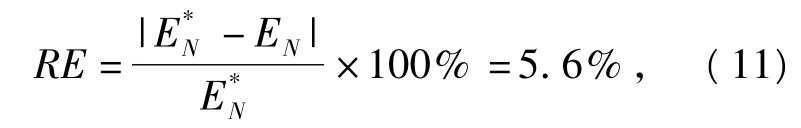
该控制方法转速有较大偏差，能量误差较大，不够精确.此外，在该方法下，试验台制动器在制动过程中消耗的能量小于所设计的路试时的制动器在制动过程中消耗的能量.这说明电流产生的扭矩不够大，无法准确测试制动器的刹车性能，可能造成高估制动器制动性能的情况.

3 模型改进

针对上述控制方法导致模拟误差大、不精确等缺点对模型加以改进.通过前一段时间的电流测量值集合，确定当前时刻的真实值进行递推控制，使得下一阶段的等价性条件尽量成立，用驱动电流对制动过程中由于机械惯量不足而缺少的能量进行补偿，这样总误差就会随着时间的增大而不断减少，其流程图见图3.改进后转速与时间关系仿真模拟图如图4所示.

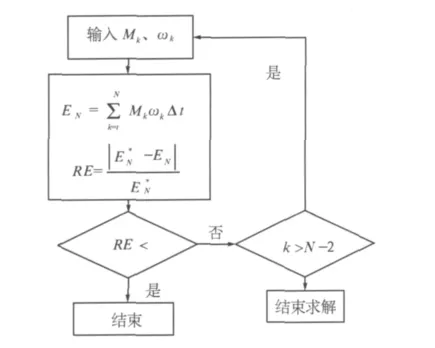
图3 驱动电流控制流程图Fig.3 Drive current control flow chart

图4 改进后转速与时间的关系图Fig.4 Speed and time relationship chart after improvement

由图4看出改进后，随着时间增大，转速实际模拟值和理想模拟值逼近，实际能量减少50 638 J，相对误差为1.59%，达到近似模拟真实汽车制动的效果，可以快速、精确、稳定地达到预定值，能够较好满足制动的要求.

4 模型评价

制动力矩的大小是衡量汽车制动效果优劣的重要指标，能否准确测量这一参数对模拟试验的效果有很大影响，可利用前一个时间段观测到的瞬时转速和瞬时扭矩，判断当前时段的模拟制动过程与理想制动过程的偏离，并以此为依据，给电流加一反馈来修正这一偏离，逐步逼近理想制动过程，得到图5的结果.

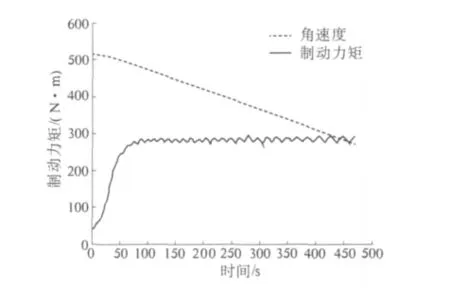
图5 改进后制动力矩与时间关系图Fig.5 Braking torque and time relationship chart after improvement

由图5可知，随着时间增加，角速度基本上均匀直线下降，制动力矩在开始有些偏差，但随着不断补偿电流，在75 s后制动力矩基本恒定且较小，进一步验证了模型的优越性，充分说明此驱动电流控制方法精度极高，鲁棒性好，抗干扰能力极强，符合要求，完成汽车车轮制动器优化.

5 结论

(1)该制动器试验台驱动电流控制方法，通过对汽车车轮制动系统的转速进行优化，解决了补偿能量的分配问题，使得补偿能量的分配达到最优，模拟值与实际值逼近.

(2)该试验台驱动电流控制方法，误差小，体积小，算法简单，抗干扰性好，鲁棒性强，可以缩短制动距离，控制效果较为理想，能够较好完成汽车制动控制系统的要求.

［1］李成，张万枝，潘旭，等.基于ADAMS的汽车平顺性建模与仿真分析［J］.郑州大学学报:工学版，2010，31(5):99-102.

［2］宋俊雅，王鹏彪，范海菊，等.制动器试验台控制系统的改进［J］.电脑知识与技术，2010，6(9):2214-2215.

［3］范海菊，张会芝，冯乃勤.基于LQG的制动器机电混合模拟系统仿真［J］.计算机仿真2010，27(8):299-302，306.

［4］宫文斌，刘安龙，江阔，等.机械惯量混合电模拟技术研究［J］.农业机械学报，2009，40(1):208-212.

［5］李永，宋健.基于制动器耗散的ABS实验方法研究［J］.公路交通科技，2004，21(3):97-101.

［6］吴广顺，张立鹏，方素香.摩托车制动器综合性能测试系统的研究［J］.机械与电子，2009(8):44-47.

［7］郝玉峰，华小洋.制动器试验方法［J］.起重运输机械，2002(7):37-38.

［8］郑志高，孙王杰.制动器试验台的控制方法分析［J］.吉林化工学院学报，2010，27(1):92-94.