惯性轮摆镇定控制器的迭代设计方法*

王轶卿，李 胜，侯保林

(1.南京工业大学自动化与电气工程学院，南京 210009;2.南京理工大学 a.自动化学院;b.机械工程学院，南京 210094)

惯性轮摆镇定控制器的迭代设计方法*

王轶卿1，2a，李 胜2a，侯保林2b

(1.南京工业大学自动化与电气工程学院，南京 210009;2.南京理工大学 a.自动化学院;b.机械工程学院，南京 210094)

针对惯性轮摆系统的镇定控制问题，提出了一种控制器迭代设计方法。该方法首先通过坐标变换将惯性轮摆系统转换为一个非线性级联系统，然后通过迭代设计和坐标逆变换，获得惯性轮摆系统的状态反馈镇定控制器，并证明了所得控制器能够使得惯性轮摆系统稳定在摆杆垂直向上的平衡位置。最后参考一个实际的惯性轮摆系统的物理参数，通过仿真，验证了所设计控制器的有效性。与已有方法相比，该方法更为简洁，更适合推广到其他欠驱动系统的镇定控制。

非线性控制;反馈镇定;欠驱动系统;惯性轮摆

0 引言

近年来，由于欠驱动机械系统的广泛应用，其建模与控制问题得到了越来越多学者的关注与研究。实际工程中存在很多欠驱动系统，如移动机器人、水面/水下舰艇、空间飞行器和柔性系统等。这些系统有一个共有特征，即系统中驱动器的个数比系统自由度的个数要少。惯性轮摆是一个典型的欠驱动系统，很多学者将其作为欠驱动系统的研究范例，并且运用很多方法来解决该系统的镇定控制问题，如监督式切换控制策略［2］、传统 Backstepping 方法［5-6］、滑模控制［7］、饱和函数法［8］等。

文献［1］将惯性轮摆从垂直向下自然平衡位置至垂直向上平衡位置的镇定问题分为两个阶段予以解决:摆起阶段和平衡阶段。在摆起阶段，给出了一种基于能量的摆起控制方法，在平衡阶段，则利用状态反馈线性化和极点配置方法设计了系统的反馈镇定控制器，最后，运用切换控制策略将上述两个阶段控制器综合到一起用于系统的摆起和平衡控制，在此控制策略的作用下，系统的摆杆可以从垂直向下的位置摆起并平衡在垂直向上的位置，但由于切换时刻不易把握，系统镇定需要多次切换和较长的时间。

文献［5-6］通过全局坐标变换将惯性轮摆的原动力学模型转化为一种非线性级联系统模型。并使用传统的Backstepping方法，构造了系统的全局镇定控制器。但在这种方法中，核心子系统的Lyapunov函数需要事先已知，否则无法推导原系统的反馈控制器。

文献［7］使用了一种和文献［5-6］相同的全局坐标变换将原系统动力学模型转化为一种非线性级联系统模型，并基于多滑模面和数值微分方法设计了系统的镇定控制器，但在这种方法中需要给出一个充分小的时间间隔ΔT。

本文则提出了一种迭代控制器设计方法，用于惯性轮摆镇定控制器设计，克服了上述控制器设计中存在的不足。论文首先给出了一种不同于文献［5-7］的坐标变换公式，将系统转化为一种更简洁的非线性级联系统模型。然后提出了一种迭代控制器设计方法为此级联系统模型设计了状态反馈控制器，并将利用坐标逆变换得到了惯性轮摆系统的镇定控制器。证明了所得控制器能够使得惯性轮摆系统稳定在摆杆垂直向上的平衡位置。最后通过仿真实验验证了所设计控制器的有效性。

1 惯性轮摆系统模型

惯性轮摆系统结构示意图如图1所示。其中:A表示惯性轮摆系统中摆杆的重心。B表示惯性轮摆系统中转动圆盘的重心。从图1中可以看出，惯性轮摆系统是一个通过安装在摆杆末端可以自由旋转的圆盘的转动来改变摆杆位置的物理摆。通过直流电机来驱动圆盘，而摆杆则没有电机带动。使用传统拉格朗日方法可以得到惯性轮摆的动力学模型［1，5-6］:

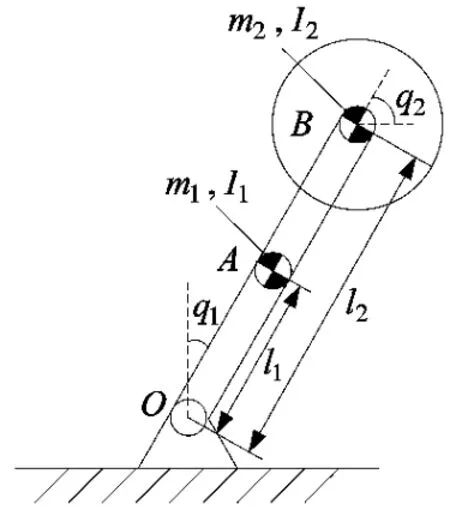
图1 惯性轮摆示意图

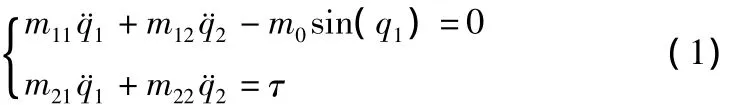
从式(1)中可以看出，惯性轮摆系统的惯量矩阵是一个常数对称矩阵，因此该系统是一个平坦对称机械系统。并且摆杆角在［0，2π)内，系统存在两个平衡位置:

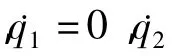
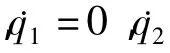
其中:第一个平衡位置是自然平衡位置，即系统在没有任何外力的作用下，偏离平衡位置后仍然能够回到此平衡位置;第二个平衡位置是受控平衡位置，即系统在没有任何外力作用下，偏离平衡位置后不能回到此平衡位置，但可以通过设计控制器，使得系统偏离平衡位置后回到此平衡位置。

1.1 模型化简与变换

根据文献［1，5］可知，转盘的转动角度对摆杆的位置没有任何影响，因此可以忽略不计，系统动力学模型的简化状态空间方程可以表示为:

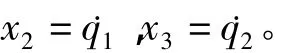
根据文献［5，6］可知，式(2)所表示的简化模型可以通过一个全局坐标变换转换成一个非线性级联系统。

为了获得一个更简洁的级联系统，本文提出了一种不同于文献［5-6］的坐标变换:

和控制输入变换:

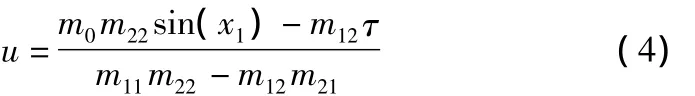
利用此变换，惯性轮摆的动力学模型(2)可以被转化为如下方程:

对比文献［1，5，7］可知，该方程也是一个具有严格反馈形式的非线性级联系统，但形式上更为简洁。

1.2 问题描述

本文主要研究如何设计一个连续状态反馈控制器使得惯性轮摆的摆杆可以从垂直向下的自然平衡位置摆起并稳定在垂直向上的受控平衡位置，即摆杆的角位置在区间［0，2π)内，q1=0，摆杆的转动速度˙q1=0，转盘的转动速度˙q2=0，转盘的位置角度q2可以为任意角度。

2 控制器设计

针对上述问题，本节给出了一种迭代镇定控制器设计方法。

首先，惯性轮摆的简化模型(5)可以分解为一个单变量仿射非线性子系统:

其中:z1为系统状态，z2为控制输入;

和一个双积分器子系统:

其中:z2，z3为系统状态，u为控制输入;

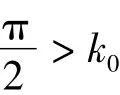
并且，为了使z2=-k0σ(cz1)，可以令

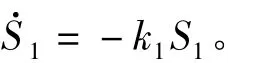
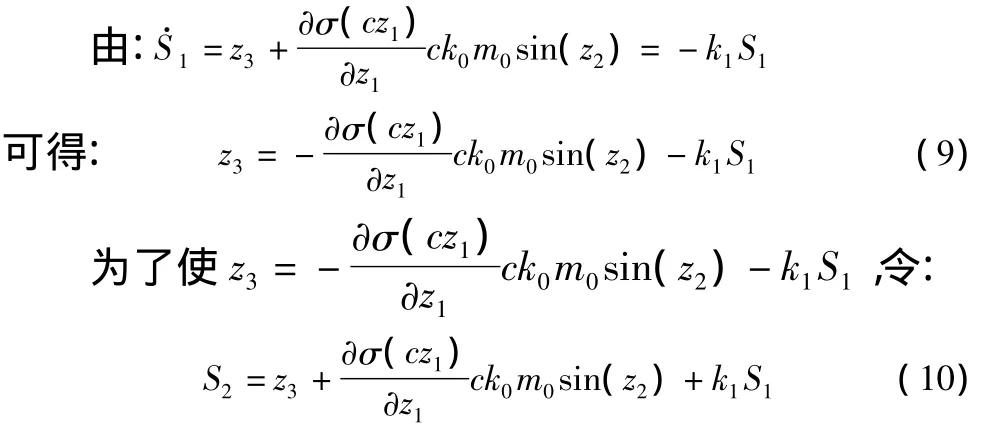
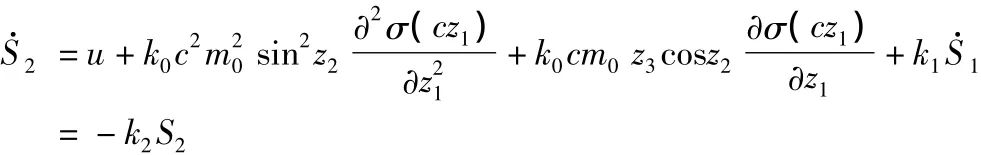
由此可得系统(5)的控制输入:

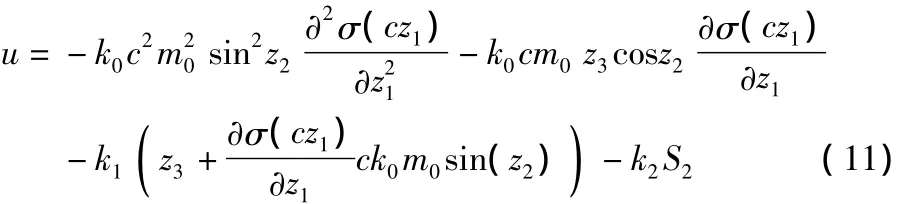
如果σ(z1)=tanh(z1)，那么

并且控制器(11)可以使得系统(5)渐近稳定在(0，0，0)。

3 稳定性分析和仿真

为了完成证明，首先给出一个用于分析级联系统稳定性的引理:

引理 1［3，6］:考虑如下级联非线性系统:

其中:f:Rn×Rm→Rn和g:Rm→Rm都是光滑函数，并且满足f(0，0)=0和g(0)=0，如果下列条件满足:

则(12)在平衡点(0，0)是全局渐近稳定的。

3.1 闭环系统稳定性分析

基于上述迭代设计过程，获得了系统(5)的一个全局反馈镇定控制器(11)，并且从式(11)和式(4)，可以得到惯性轮摆系统的全局反馈镇定控制器:

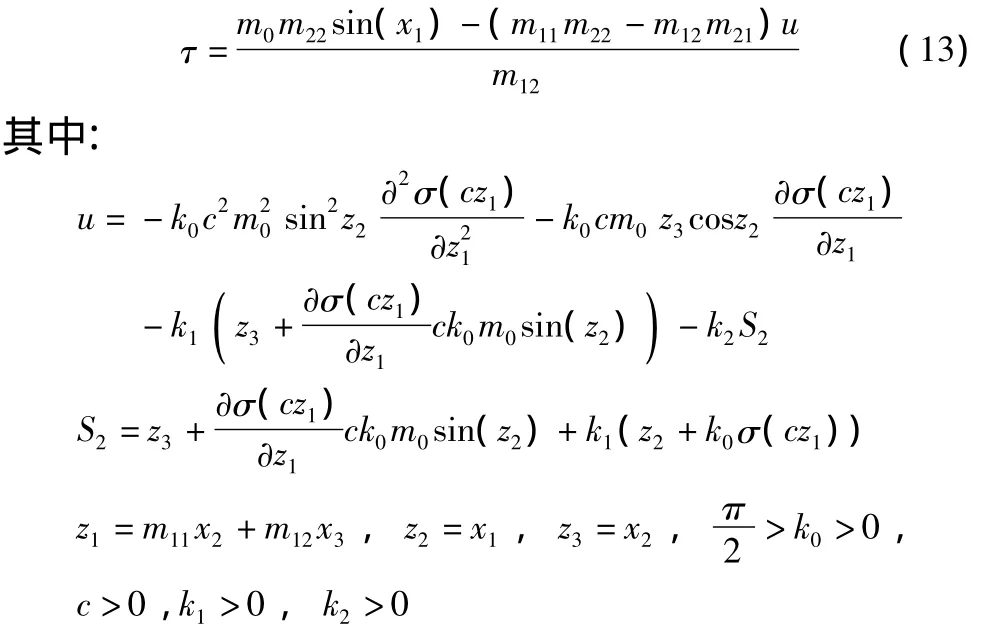
由第3节所得结论和上述坐标变换，可以得为如下定理:

定理1:在控制器(13)的作用下，系统(2)在平衡点(0，0，0)是全局渐近稳定的。

证明:首先选择坐标变换:

当控制输入为式(11)时，系统(5)可以被转换为:

基于引理1，可知系统:

在(0，0)是渐近稳定的，因为:

再次基于引理1，可知系统:

在(0，0)是渐近稳定的，其中:

因此，系统(5)在控制器(11)的作用下，系统是渐近稳定的。

同时，因为坐标变换(3)和控制输入(4)是全局同胚变换，因此系统(2)在控制器(13)作用下的渐近稳定性与系统(5)在控制器(11)作用下的渐近稳定性是等价的。即系统(2)在控制器(13)作用下在平衡点(0，0，0)是全局渐近稳定的。

3.2 惯性轮摆仿真

下面通过一个仿真来验证所设计控制器的有效性，为了和已有控制器进行比较，本文使用了和文献［1，5，7］中一致的参数。参数如下所示:

由此可得:

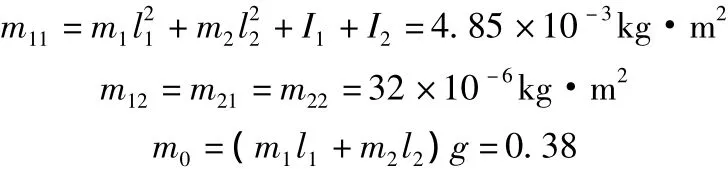
设置控制器(13)的参数为c=30，k0=1，k1=12，k2=2。惯性轮摆的初始状态为:q1=π，˙q1=0，˙q2=0。在控制器(13)的作用下，惯性轮摆的状态轨迹和控制输入如图2所示。

图2 惯性轮摆系统各状态和控制输入

仿真结果说明本文所提控制器可以使惯性轮摆的摆杆从垂直向下的位置摆起并平衡在垂直向上的位置。为了获得更快的摆起速度和收敛速度，需要更大的电机力矩，与文献［5］的仿真结果相比，系统各状态能够更快地收敛至平衡位置，但电机最大力矩也比文献［5］中的最大力矩更大一些。

4 结束语

本文针对惯性轮摆的全局镇定问题，提出了一种迭代控制器设计方法和一种全局坐标变换公式，利用此坐标变换公式和控制器设计方法，可以获得一个更简洁的变换结果和反馈镇定控制器。所设计的状态反馈控制器可以使得系统各状态渐近收敛于平衡位置。仿真结果给出了所设计控制器的效果和性能。本文所提出的迭代控制器设计方法也可以用于一类可以转化为级联形式的欠驱动系统，如TORA系统等。

［1］R.Xu，Ü. Özgüner:Sliding mode control of a class of underactuated systems.Automatica，2008，44(1):233-241.

［2］M.W.Spong，P.Corke，R.Lozano.Nonlinear control of the Inertia Wheel Pendulum Automatica，2001，37(11):1845-1851.

［3］E.D.Sontag.Further Facts About Input To State Stabilization.IEEE Transaction Automatic and Control，1990，35(4):473-476.

［4］R.Olfati-Saber.Control of underactuated mechanical systems with two degrees of freedom and symmetry.Proceeding of American Control Conference，Chicago，IL，2000，6:4092-4096.

［5］R.Olfati-Saber.Global Stabilization of a Flat Underactuated System:the Inertia Wheel Pendulum.Proc.of the 40th Conference on Decision and Control，Orlando，FL，2001，4:3764-3765.

［6］R.Olfati-Saber.Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles.PhD thesis，Massachusetts Institute of Technology，Department of Electrical Engineering and Computer Science，February 2001.

［7］N.Qaiser，S.B.Tariq，N Haq，T.Aziz.A novel nonlinear implicit sliding surface controller design for inertia wheel pendulum.ROCOM'10 Proceedings of the 10th WSEAS international conference on Robotics，control and manufacturing technology.HangZhou，China，2010:21-25.

［8］C.F.A.Ibanez，O.O.G.Frias.M.S.S.Castanon.controlling the strong damping inertia wheel pendulum via nested saturation functions Computación y Sistemas，2009，12(4):436-449.

A Recursive Design Method for Stabilization of the Inertia Wheel Pendulum

WANG Yi-qing1，2a，LI Sheng2a，HOU Bao-lin2b
(1.School of Automation and Electronic Engineering，Nanjing University of Technology，Jiangsu 210009，China;2a.School of Automation;2b.School of Mechnical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China)

Aimed at the stabilization problem of the Inertia Wheel Pendulum system，a recursive design method of stabilization controller was proposed.In this method，the Inertia Wheel Pendulum system was transformed into a nonlinear cascade form through a coordinate transformation firstly.And through a recursive design procedure and inverse coordinate transformation，a state feedback controller of Inertia Wheel Pendulum system with explicit form was obtained.And then the stability of the Inertia Wheel Pendulum system under the proposed controller at position，where the pole was vertial up，was proved.Finally，the effectiveness and performance of the proposed stabilization controllers for an inertia wheel pendulum system whose parameters were taken from a real-life model of the IWP was shown through simulations.Compared with some existing method，the proposed method in this paper was more simplicity and suitable to expand to the stabilization of other underactuated systems.

nonlinear control;feedback stabilization;underactuated system;inertia wheel pendulum

TH16;TG65

A

1001-2265(2012)12-0041-04

2012-04-03;

2012-09-25

国家自然科学基金(51175266);江苏省高校自然科学研究计划项目(12KJB510008);南京工业大学青年教师学术基金(39710013)

王轶卿(1981—)，女，河北三河人，南京工业大学自动化与电气工程学院讲师，博士生，主要从事欠驱动系统控制、非线性控制、智能控制等方面的研究，(E-mail)wangyiqing1112@163.com。

(编辑 李秀敏)