四足机器人步幅、步频与扭矩和能耗关系研究*

李 军，苗新聪，张晓宇

(西北工业大学机电学院，西安 710072)

四足机器人步幅、步频与扭矩和能耗关系研究*

李 军，苗新聪，张晓宇

(西北工业大学机电学院，西安 710072)

步频与步幅是影响四足机器人运动速度的主要因素，针对不同步频与步幅的耦合状态，分别研究了步频与步幅独立变化对机器人关节扭矩与能耗的影响，并对多种步幅下步频变化引起速度增加对运动质量的影响进行了分析与比较。得出能耗对步频参数的提高更为敏感，关节扭矩与步幅参数的变化有直接的关系，同时肘式关节在运动中所需提供的驱动力矩要小于膝式关节，最后给出了不同参考标准下步频与步幅的优化耦合范围，结论能够作为四足机器人结构设计与运动优化的参考。

四足机器人;步频;步幅;能耗

0 引言

动物的步行调节主要通过改变步频和步幅来实现，国内外学者对包括人在内的多类动物在运动中步频和步幅的变化与优化关系进行了大量的研究。对于生物来讲，步频更多地是与神经过程的灵活性和快肌纤维的含量有关，而步幅更多地是受关节屈伸幅度的限制。过于提高步频会造成肌肉的疲劳，过于增大步幅会使肌肉组织的负荷加重，同时上述参数的变化还会影响到能量的消耗，因此针对特定的运动速度，在一定程度上均有一个最佳步频与步幅的耦合范围［1-4］。此外步频步幅的提高均能使速度得到增加，步幅的增加与步频的增加都会造成关节扭矩于地面接触力的增大［5］，有研究表明从多种参数的优化关系来看，步幅的增加更优于步频的增加［6］。

对于以电机驱动的四足步行机器人，设计成型后其关节输出力与输出速度取决于驱动器的特性参数，其中机器人运动步频取决于驱动器的输出速度，机器人的运动步幅取决于机器人的关节自由度范围，在运动速度调整的过程中，只要驱动器所需提供的驱动力与驱动速度在特性曲线包络的范围内，机器人就能按照设计要求实现可靠的步行运动。而生物肌肉为一种串并联弹性系统，其输出特性与电机输出特性不同，同时其具有疲劳效应，此外机器人在结构上是经过了仿生的简化，且多为刚性环节联接缺少弹性缓冲，与生物的柔性结构也有较大不同。因此机器人的步频步幅等参数变化对每个关节驱动力输出与能耗的影响关系与生物参数不会完全相同。目前四足机器人领域中研究步频步幅对运动状态影响的文献仍较少，曾有日本学者在研究地面摩擦、运动速度与能耗的关系中，提到了运动速度与能量消耗的问题，但是仍没有对影响运动速度的步频与步幅与能耗关系进行更深入的讨论［7］，因此本文将进一步对机器人的运动参数最佳耦合范围进行研究，分析运动中步频、步幅改变对运动速度、关节扭矩以及能量消耗等参数的影响，用于机器人的优化运动控制。

本文分别研究四足机器人对角步态固定步频下步幅逐步加长以及固定步幅(小、中、大三种)下步频逐步提高对步行速度、驱动力矩，能耗等参数的影响，并进一步做出比较，以得出机器人最佳的步幅、步频取值范围与耦合关系。

1 样机介绍

所设计的四足机器人几何关系参数如图1所示，整体具有12个自由度，为膝肘式全对称结构。其中4个髋关节可实现大腿相对于机身外摆/内收与前后拨动两个自由度，膝、肘关节可实现小腿相对于大腿的转动。四足机器人可实现空间内6个自由度的全方位运动。

图1 自由度与结构形式

定义机身长度(髋关节转轴纵向位置关系)为L，宽度(髋关节转轴横向位置关系)为W，髋部长度为L1，大腿长度为L2，小腿长度为L3，His表示初始状态机身高度。表1为初始状态运动学参数值列表，表2位动力学参数值列表。

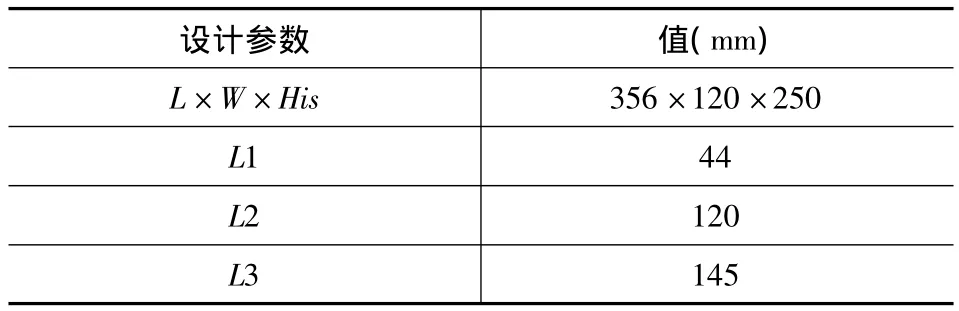
表1 四足机器人运动学参数表

表2 四足机器人动力学参数表

2 试验设计

实际机器人运动中，关节扭矩与能耗难以有效测量，对地面反冲击力与摩擦状况建模也较为复杂，因此本文采用仿真的方法进行研究，采用Adams与Matlab联合仿真的方式进行机器人动力学仿真以及相关参数的测定。在Simulink环境下进行机器人运动轨迹规划，将步长L与步频f进行参数化设计，根据对角步态的多关节耦合关系进行相位与相序的调制，依托Adams动力学模块进行交互式仿真。仿真交互示意如图2所示。

图2 联合仿真环境示意图

为研究采用不同步频、步幅对关节扭矩、能量消耗等参数的影响，本文以速度作为比较指标，将步频与步幅折算为速度，以速度为基准进行相关参数的比较。其中纵向比较单一步频或步幅提高而另一值保持不变的情况下，引起的速度提升对关节扭矩与能耗等参数的影响。横向比较不同步频或步幅下，其中一值变化引起速度提升对关节扭矩与能耗等参数的影响。由于四足机器人步长变化范围要大于步频变化范围，因此本文特别地对小步幅、中步幅、大步幅三种特定情况下，步频提高造成速度增加对关节扭矩与能耗等参数的影响进行横向比较。

3 步行规划设计

由于四足动物在对角步行中运动速度基本保持恒定，且身体高度基本固定，因此设计机器人在步行时以恒定的速度V前进，其运动轨迹如图3所示，以右前足为设计对象，设计其足点轨迹线由上半椭圆与直线构成，且在两端采用圆弧过渡，以使机器人的步行轨迹具有柔滑性。机器人整体运动均依照此轨迹按照对角步态相序相位进行协调。

设计步频f(周期T)，机身高度H，步高H1，过渡圆弧半径r、步幅L可调，由于本文主要研究步频与步幅的关系，因此在轨迹规划中对其余参数采用固定值，初始状态下足点位置处于髋关节点的正下方，且步幅相对于初始状态点前后对称，其中支撑相与摆动相时间各占0.5T。

4 仿真试验与分析

在Adams与Matlab环境下进行四足机器人交互式运动仿真，设计Adams环境下四足机器人与地面的接触参数如表3所示，采用固定步长求解器，定义仿真步长0.002s，仿真交互时间间隔为0.002s，设计四足机器人仅作直线步行运动，并设置传感器:当机器人运动距离达到1m时，停止仿真。

图3 右前足行走足轨迹规划模型

设计机器人初始运动步长0.03m，同时为保证机器人动态运动的平稳性，设计最小初始步频为1.667Hz(周期T=0.6s)。研究步长和步频分别提高的状态下所引起的速度增加对关节扭矩、能量消耗的影响。同时，为保证多组数据有共同的比较标准，将运动速度限制在6m/min～19m/min之间。由于机器人设计为电机驱动，通过减速后，电机的持续输出力矩为10Nm，最大堵转转矩为75Nm，最大输出速度为90rpm，将此参数作为机器人能否可靠实现运动的评判标准。由于机器人采用对称方式进行运动，因此仅研究一组对角腿的扭矩与功耗即可反映机器人的实际运动情况，本文选取右前腿与左后腿作为研究对象，其中每条腿包含两个关节，其中右前小腿关节为肘关节，左后小腿关节为膝关节。

设计机器人运动环境为平整地面，机器人机身高度为初始状态，步高为0.03m，仿真第一个周期为初始状态准备，机器人不运动，第二个周期与第三个周期为步态调整期，机器人做原地踏步运动，第四个周期开始机器人按照对角步态步行规划开始直线前进。仿真试验环境如图4所示。

表3 Adams接触参数表

图4 四足机器人仿真环境

4.1 步频固定步幅提高

设定四足机器人运动步频1.667Hz(对应步行周期T为0.6S)不变，步幅由0.03m逐步增加到0.095m(平均分布14个节点)，对应速度从6m/min提高到19m/min。对应所需研究的参数，将节点值用spline线进行连接。图5为该步频下，单独提高步幅对运动参数的影响趋势。a图为所研究的一组对角腿系在支撑相阶段稳定运动所需扭矩的最大值变化趋势;b图为腿系进入支撑相瞬间，足点受地面冲击力作用，引起驱动器的瞬间输出，其最大允许值为驱动器末端的堵转输出;c图为所研究的一组对角腿系四个关节在1m的运动间隔内所消耗的功与功之和。

图5 步频固定步幅提高对运动参数的影响

由上图可以看出随着步幅的增加，关节扭矩与功耗都在增加，由于驱动器输出极限参数的限制，在步长为0.095m处，最大持续关节扭矩输出值与抗冲击力瞬间爆发值均已达到最大要求，此种情况下其允许极限速度是19m/min。其中功耗在后期有一定的波动跟机器人步行周期相关，研究表明功率的提升主要是在对抗冲击力方面，因此在1m距离限制内，步行终止时间在支撑相0时刻的前后能够造成功耗的较大不同，同时步行速度的提高引起地面接触情况变化，会导致驱动功率输出的改变，但整体上各参数均呈上升的趋势。

从a图和b图可以看出在步幅增大到一定程度后(s=0.08m)，髋关节驱动输出力矩会以较大的幅度增加，这与落足点位置以及地面冲击力大小和方向相关，因此在这种情况下，随着步长的再度提高，机器人的运动效果会变差。

4.2 步幅固定步频提高

分别研究步幅为0.03m、0.05m、0.07m情况下，步频从稳定步频1.667Hz逐步提高，研究速度提高所引起的扭矩与能耗的变化。

4.2.1 小步幅情况

设定四足机器人运动步幅0.03m，步频由1.667Hz增大到5Hz(对应步行周期T变化为0.6S～0.2S)(分布9个节点)，对应速度从6m/min提高到18m/min。对应所需研究的参数，将节点值用spline线进行连接。图6为该步幅下，单独提高步频对运动参数的影响趋势。a、b、c图描述与前述相同。

图6 步幅固定步频提高对运动参数的影响

由上图可以看出随着步频的增加，运动中的稳态最大持续关节扭矩增加幅度较平缓，但是在步频提高至2.8Hz以后，驱动抵抗冲击力的瞬间爆发值以较大幅度提高，步频提高至3Hz时已经难以满足所需提供的瞬间输出力矩。同时能量消耗也以较大的幅度提高，相对于单独提高步幅，折算为相同的运动速度比较，其能耗相差2倍，因此可以看出，小步幅下单纯的步频提高对冲击扭矩与能耗影响较大，可以得出小步幅下的高步频，增加了腿系的往复摆动次数，受系统惯量的影响，过多的摆动动作增加了能量的消耗，同时步频提高也使足点与地面的接触状态变得更恶劣。此种情况下其允许极限速度是10.3m/min。

4.2.2 中步幅情况

设定四足机器人运动步幅0.05m，步频由1.667Hz增大到3.13Hz(对应步行周期T变化为0.6S～0.32S)(分布8个节点)，对应速度从10m/min提高到18.75m/min。对应所需研究的参数，将节点值用spline线进行连接。图7为该步幅下，单独提高步频对运动参数的影响趋势。a、b、c图描述与前述相同。

图7 步幅固定步频提高对运动参数的影响

由上图可以看出随着步频的增加，运动中的稳态最大持续关节扭矩增加幅度较平缓，在步频提高至2.8Hz以后，驱动抵抗冲击力的瞬间爆发值以较大幅度提高，步频提高至2.92Hz时已经难以满足所需提供的瞬间输出力矩，同时能量消耗也以较大的幅度提高，，此种情况下其允许极限速度是17.2m/min，相对于单独提高步幅，折算为相同的运动速度比较，其能耗基本相同，但是稳态最大持续关节扭矩要稍小一些。可以得出中步幅下的过高步频，同样会使运动质量变坏。

在此种情况下有一个特殊现象，即是右前腿肘关节的最大持续关节扭矩输出值随着速度的提高其输出值呈下降趋势，其参数值也要远小于其与机体各关节的值，这是由地面摩擦力、支持力与小腿的位姿特征决定的，从一个侧面说明采用肘式关节的机器人在运动中所需提供的扭矩较小，肘关节的驱动器选取可以采用较小的功率参数。

4.2.3 大步幅情况

设定四足机器人运动步幅0.07m，步频由1.667Hz增大到2.174Hz(对应步行周期T变化为0.6S～0.46S)(分布5个节点)，对应速度从14m/min提高到18.26m/min。对应所需研究的参数，将节点值用spline线进行连接。图8为该步幅下，单独提高步频对运动参数的影响趋势。a、b、c图描述与前述相同。

图8 步幅固定步频提高对运动参数的影响

由上图可以看出随着步频的增加，运动中的稳态最大持续关节扭矩增加幅度较平缓，而驱动抵抗冲击力的瞬间爆发值提升幅度较大，到1.86Hz就已经超过了允许范围，此种情况下其允许极限速度是15.6m/min。相对于单独提高步幅，折算为相同的运动速度比较，其能耗基本相同，稳态最大持续关节扭矩也基本相同。可以得出大步幅下运动质量对步频更为敏感，小幅度地增大步频就会加剧运动的不稳定性，导致足点与地面的接触状态变得更恶劣，增大抗冲击扭矩。

4.3 试验结果分析

通过以上参数的图示与分析，可以得出以下结论。

(1)机器人在运动中，单独提高步频比单独增大步长使速度提升造成的能量消耗更多，证明多数的能量消耗在摆动相以及抵抗地面冲击力上。腿系往复频率较大的情况下，增大了足点与地面的接触次数，同时腿系的惯量也是高频摆动下的扭矩输出增大的一个影响因素。

(2)运动步频过大会导致运动状态向恶劣的方向发展，使机器人驱动输出力矩过快增长，能耗加大。

(3)对于膝肘式结构的四足机器人，在直线水平运动中其肘关节处所需提供的稳态最大持续扭矩要小于膝式关节所需提供的扭矩，在某些特殊情况下，地面摩擦力与支持力的耦合作用下，随着速度增大其所需提供的扭矩有变小的趋势。而膝式关节在运动中因位姿约束，在一定阶段内所需的瞬间抗冲击输出扭矩较小。因此在机器人设计时，可根据情况合理设计构型形式。

(4)较大的步幅与较小的步幅对机器人的最大允许速度有一定的限制，在横向比较中，受驱动系统输出特性的影响，中等步幅能够在耦合适宜的步频时达到较高的运动速度，大步幅下则能够实现较低的能量消耗，最差的运动效果是小步幅高步频。

(5)纵向比较来看，大步幅(受机器人自由度限制)与低步频(须保证一定的稳定性)耦合能够实现较高的运动速度与较小的能量消耗，从另一个侧面反映运动质量对步频较为敏感，因此如果仅考虑驱动器输出能力(低功率密度驱动)，应选取中步幅与中步频耦合，如果仅考虑系统能耗(高功率密度驱动)，则采用大步幅与低步频耦合。

5 结束语

通过比较与分析步频与步幅增加引起速度提高对关节驱动扭矩与能耗的影响状态，得出不同评价标准下的参数优化耦合关系，为四足机器人设计与优化控制提供了参考依据。

［1］郭胜.世界男子400M运动员步态变化对速度的影响［J］. 武汉理工大学学报，2010，32(18):169-174.

［2］谢伟，周玉.从步长、步频的角度分析我国男子百米跑成绩滞后原因［J］.体育科技文献通报，2010，18(1):16-17.

［3］F.Danion，E.Varraine，M.Bonnard，et al.Stride variability in human gait:the effect of stride frequency and stride length［J］.Gait＆ Posture，2003(18):69-77.

［4］Anne Delextrat，Dionne Matthew，Daniel D.Cohen，et al.Effect of stride frequency on the energy cost of walking in obese teenagers［J］.Human Movement Science，2011(30):115-124.

［5］Lara Allet，Herman IJzerman，Kenneth Meijer，et al.The influence of stride-length on plantar foot-pressures and joint moments［J］.Gait＆ Posture，2011(34):300-306.

［6］Yunpeng Huang，Onno G.Meijer，Jianhua Lin.The effects of stride length and stride frequency on trunk coordination in human walking［J］.Gait＆ Posture，2011(31):444-449.

［7］Hiroshi Takemura，Masato Deguchi，Jun Ueda，et al.Slipadaptive walk of quadruped robot［J］，Robotics and Autonomous Systems，2005(53):124-141.

The Research on Effect of Stride Frequency and Stride Length on Joint Torque and Energy Cost in Trotting of Quadruped Robot

LI Jun，MIAO Xin-cong，ZHANG Xiao-yu
(School of Eectromechanics，Northwestern Polytechnical University，Xi’an 710072，China)

Stride frequency and stride length are main elements affecting the speed of quadruped robot.In this paper，we study the effect of these two independent variables on the joint torque and energy consumption according to the coupling between them.Furthermore，we analyze and compare the effect of the increase of the speed，which is caused by the frequency with multiple stride lengths，on the locomotion behavior.From the simulation results，we observe that the energy consumption is more sensitive to the increase of the frequency，the joint torque is directly related to the change of stride length，and the driving torque required by the elbow-styled joint is less than that by the knee-styled joint.In addition，we figure out the optimal range of coupling between stride frequency and stride length based on various frame of references.This research might benefit to the structure design and motion optimization of quadruped robots.

quadruped robot;stride frequency;stride length;energy cost

TP242

A

1001-2265(2012)12-0010-05

2012-06-12

国家863计划主题项目(2011AA041001)

李军(1981—)，男，河南驻马店人，西北工业大学机电学院博士研究生，主要研究方向为智能仿生机器人，(E-mail)lijun956@yahoo.com.cn。

(编辑 赵蓉)