基于遗传算法的主轴回转误差评价方法*

高慧中，刘 飞，梁 霖，徐光华，2，黄付中

(1.西安交通大学机械工程学院，西安 710049;2.西安交通大学机械制造系统工程国家重点实验室，西安 710054;3.大连机床(数控)股份有限公司，辽宁 大连 116033)

基于遗传算法的主轴回转误差评价方法*

高慧中1，刘 飞1，梁 霖1，徐光华1，2，黄付中3

(1.西安交通大学机械工程学院，西安 710049;2.西安交通大学机械制造系统工程国家重点实验室，西安 710054;3.大连机床(数控)股份有限公司，辽宁 大连 116033)

针对主轴回转误差评价问题，提出了基于遗传算法的主轴回转误差评价方法。建立了基于遗传算法的最小包络圆法误差计算模型。通过研究精密主轴回转误差特征，利用遗传算法与最小包络圆评价方法，获得了基于遗传算法的主轴回转误差评价方法，并在精密磨齿机主轴上进行实验验证与应用。结果表明，基于遗传算法的最小包络圆主轴回转误差评价方法具有良好的评价效果。

主轴回转误差;最小包络圆;遗传算法

0 引言

机床主轴回转精度是机床的主要精度指标之一，直接影响着被加工零件的加工精度及表面粗糙度。主轴的回转误差是一项综合性的误差，它是主轴的实际回转轴线相对于平均回转轴线(实际回转轴线的对称中心线)的最大变动量。通常，主轴回转误差包括径向回转误差、轴向误差和角度摆动误差。但是对于机床主轴来说，其安装结构促使轴向误差和角度摆动误差较小，在一定的条件下可以利用主轴径向回转误差来衡量主轴回转精度［1-10］。

对于单截面测量来说，由于主轴截面轮廓误差较小，动态轴心波动将成为影响主轴回转误差的主要因素，而利用误差理论评价动态轴心轨迹的研究还相对较少。为此，本文在研究主轴径向动态回转误差的基础上，提出对主轴轴心轨迹进行评价，利用基于遗传算法的主轴回转误差最小包络圆法对主轴径向动态回转误差进行评价。基于遗传算法的主轴动态轴心轨迹评价方法可以有效的保障包络圆半径值达到最小，同时也符合最小条件的要求。

1 主轴回转误差与遗传算法基本原理

1.1 主轴回转误差评价方法

主轴回转误差决定工件的形状精度和表面质量，机床加工精度愈高，加工精度受主轴回转误差的影响所占比例愈大，这说明主轴回转精度在机床动态性能指标中的重要地位。提高机床主轴回转精度是评价和提升当前机床精度和整机性能的重要手段。在主轴轴心运动误差轨迹的基础上，求解出准确的运动误差量值，即是主轴回转误差评价。一般情况下采用回转精度来反映主轴回转误差的大小。

由于最小包络圆的直径值是评价回转误差的最客观指标，因此如何选择最小包络圆的直径值来评价主轴回转误差将成为本文讨论的重点。回转误差数据最小包络圆地准确求解，直接关系到分离精度的评价。针对这个问题，本文采用遗传算法概率寻优的方法来计算经过误差分离后的主轴径向回转误差数据的最小包络圆，经过不断优化，最终得到准确的最小包络圆，从而用包络圆的直径来评价回转精度。

1.2 遗传算法的基本原理

遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现(即基因型)是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

利用遗传算法求径向回转误差数据的最小包络圆，实际上也就是求一系列平面点列的包络圆问题，通过建立求平面点序列包络圆的数学模型，把求最小包络圆的问题转化成函数优化问题，然后采用遗传算法将此函数的最优解问题得到解决［1］。

2 建立最小包络圆求解数学模型

对于给定平面点序列{Qi}={(xi，yi)}，i=1，2，…，n}的包络圆是指使得序列的所有点都在圆周上或者圆内区域的圆。显而易见，一组平面点列有无穷个包络圆，而在这些包络圆中，半径最小的称之为平面点序列的最小包络圆。

根据定义，如果要求得一组点序列{Qi}的最小包络圆，最重要的是计算出圆心(a，b)和半径r，使得满足下列条件:

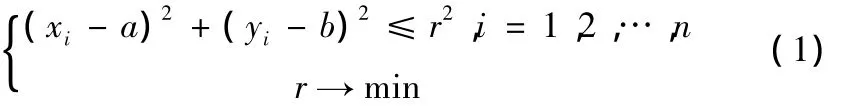
下面引入点序列{Qi}的包容矩阵，令:

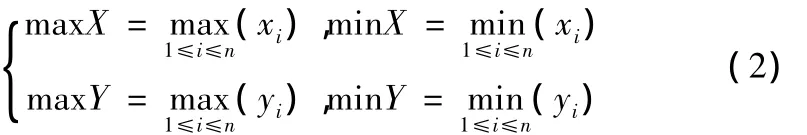
分别将点(MinX，MinY)，(minX，maxY)，(MaxX，minY)，(maxX，maxY)设为矩形的顶点，点Qi(i=1，2，…，n)必然都在矩形内，此矩形称之为点序列{Qi}的包络矩阵。而最小包络圆与包络矩阵关系如下:

设平面点序列{Qi}的最小包络圆半径为r，圆心为(a，b)可以证明有以下关系:

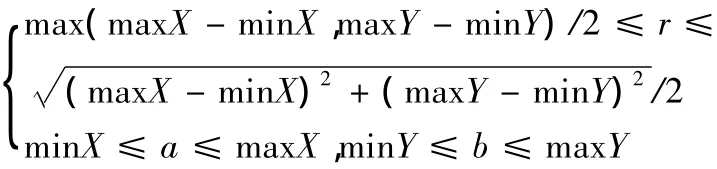
即最小包络圆的圆心(a，b)在包络矩形中。

序列{Qi}包络圆半径的函数可定义为:

一是发挥中物院科技资源优势，建立技术创新服务平台。Z公司以中物院丰富的科技资源和科研能力为依托，与中物院化工材料研究所联合共建四川省新材料研究中心，与中物院机械制造工艺研究所联合共建智能制造公共技术服务平台。面向孵化器内入驻企业辐射绵阳市其他中小微企业提供技术支持和技术创新服务。此外，Z公司还整合了中物院流体物理研究所、中物院核物理与化学研究所、中物院激光聚变中心等院内各所科研仪器，建立中物院国防科学仪器共享平台，为孵化器内入驻企业和其他中小微企业提供检测、检验服务。

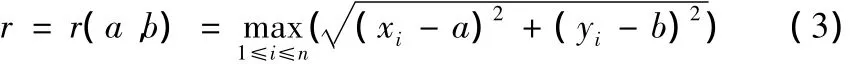
式中:minX≤a≤maxX，minY≤b≤maxY，因此，求最小包络圆的半径就转化为求当a，b为何值时，函数r(a，b)最小。因此，函数r(a，b)就成为遗传算法求解的目标函数。

3 基于遗传算法的最小包络圆计算法

3.1 基于遗传算法的最小包络圆计算过程

遗传算法的计算过程如图1所示，包括:选择编码方式、产生初始群体、计算初始群体的适应性值、如果不满足条件{选择、交换、变异、计算新一代群体的适应性值}。

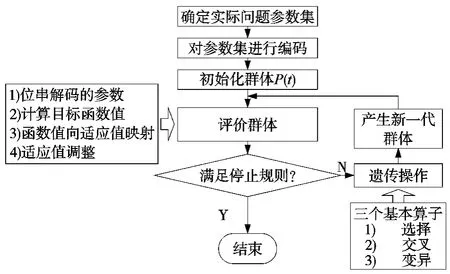
图1 遗传算法的计算过程

个体编码是一个二元数O=(a，b)，其中(a，b)为包络圆圆心，这里a∈［minX，maxX］，b∈［minY，maxY］。

(1)种群初始化

随机产生Q-Size个个体(Q-Size为种群的规模):Oi=(a，b)，i=1，2，…，Q-Size，其中，ai=minX+(MaxX-MinX)×Randi1，bi=minY+(MaxY-MinY)×Randi2，Randi1和Randi2是［0，1］区间内的随机数。

(2)遗传操作

对于个体Oi=(ai，bi)，r=r(ai，bi)为相应包络圆半径。定义适应度函数为:f=f(Oi)=1/r(ai，bi)，其适应度函数值越大说明个体越优，即平面点列{Qi}的包络圆半径越小。

2)选择操作

3)交叉操作

采取线性组合交叉的方式，以交叉概率Qc选择两个个体进行交叉运算。如个体Oi=(ai，bi)和Oj=(aj，bj)交叉生成两个新个体为:

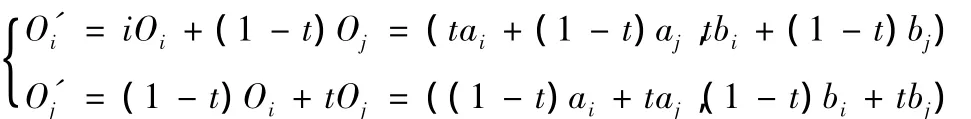
其中，0∠t∠1，为线性组合系数，是预先设定的常数。

4)变异操作

以变异概率Qm选择个体，然后以0.5的概率选择个体中某个位置进行变异操作，也就是用［minX，maxX］或者［minY，maxY］区间内的随机数取代。进行变异操作可以保持个体的多样性，而不致于陷入局部收敛。例如，个体Oi=(ai，bi)选择第一个基因作变异操作得到的新个体为:Oi=(ai，bi)=(minX+(maxX-minX)Rand，bi)，Rand为［0，1］区间上的随机数。

这样在遗传操作中，将上一代的最优个体保留下来，加快了收敛速度。

3.2 基于遗传算法的最小包络圆仿真计算

已知点列{Qi}={(xi，yi)}，i=1，2，…，N，设 θ=0～2.π，将其N等分。设当N=180，{Qi}=0.5+0.3(1.2cos(θ)-0.8sin(θ)+0.1sin(2θ)+0.2cos(3θ)-0.6cos(6θ)+0.3sin(13θ)+0.7cos(20θ))时，生成的平面点序列如图2所示。求此平面点列{Qi}的最小包络圆。

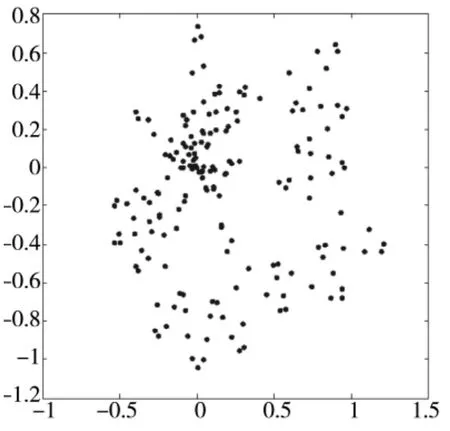
图2 平面仿真序列

采用上述的遗传算法进行求解，设定种群规模为100，变异概率Qm=0.01，交叉概率Qc=0.6，遗传计算最大代数为200，经遗传算法优化方法计算得最小包络圆如图3所示，其圆心为:(0.34，-0.13)，半径为:r=0.97。

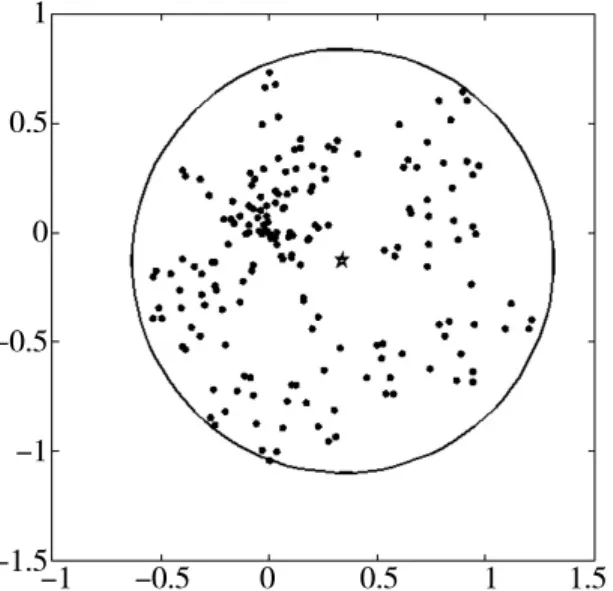
图3 遗传算法求得最小包络圆

4 基于遗传算法的主轴回转误差评价

为了进一步验证基于遗传算法的主轴回转误差评价方法的可行性，对某精密磨齿机砂轮主轴进行实验分析，其中机床的砂轮轴是通过皮带轮与主轴来传递动力的，传动比为3.5，实验测试现场如图4所示，分别在主轴转速500rpm和4000rpm进行数据采集，采样频率为12.8k，计算得每周采样点数分别为5376和672。

图4 主轴回转误差测试现场

图5所示为主轴转速500rpm下的传感器采集时域波形，根据本文算法计算得轴心轨迹如图6所示，其中圆心坐标为(0.01，0.03)，计算得轴心轨迹的最小包络圆直径值为1.1μm。

图5 两只传感器单周期采样数据图

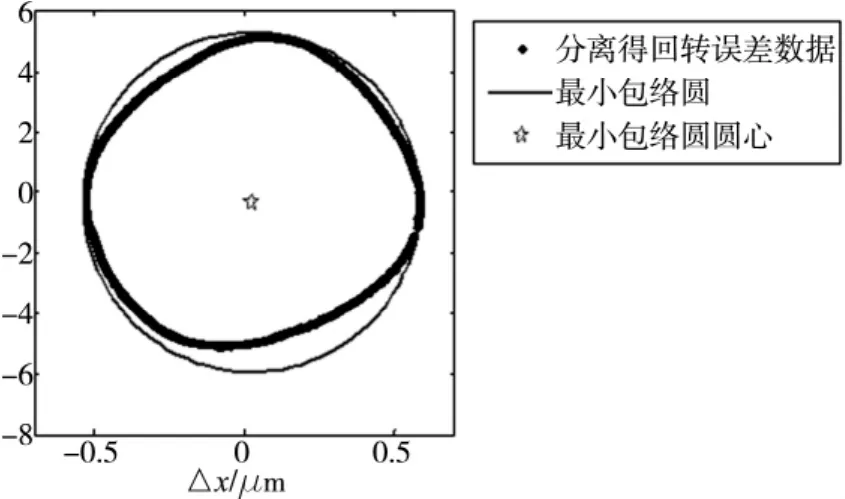
图6 主轴500rpm时轴心轨迹

图7所示为主轴转速4000rpm下的传感器采集波形，根据算法计算得轴心轨迹如图8所示，其中圆心坐标为(0.04，0.02)，计算得轴心轨迹的最小包络圆直径为:1.2μm。

在以上计算结果的基础上，回转误差结果对比如表1所示。

图7 两只传感器单周期采样数据图

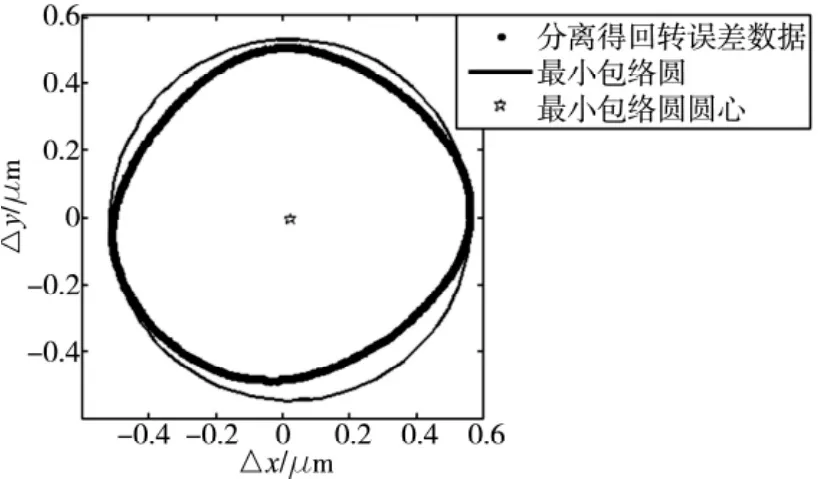
图8 主轴4000rpm时轴心轨迹

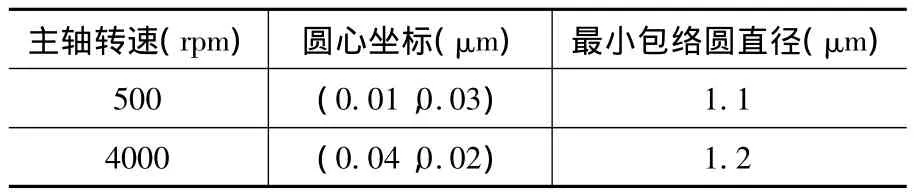
表1 回转精度计算结果对比

根据上述实例的结果显示可以看出，基于遗传算法的最小包络圆求解方法可以达到很好的效果。将其应用于主轴回转误差评定中，可快速准确计算得主轴的回转精度。

5 结论

本文在研究了主轴回转误差评价的基础上，针对实际主轴回转误差检测中存在的问题，提出了基于遗传算法的主轴回转误差评价方法。对精密磨齿机主轴进行实验分析，对评价方法进行了验证和应用。结果表明，基于遗传算法的最小包络圆主轴回转误差评价方法具有很好的效果。并可以快速准确的计算得到主轴回转误差量值。

［1］王洪发，刘婕.用遗传算法求平面点列的最小包络圆［J］. 南昌大学学报，2007，29(4):384-386.

［2］熊有伦.精密测量的数学方法［M］.北京:中国计量出版社，1989.

［3］彭万欢，赵午云，陶继忠，等.精密主轴回转误差测试的偏心分析［J］.机械设计与制造，2008(12):83-85.

［4］主轴径向回转误差评定的最小径向间距算法［J］.振动、测试与诊断，1991，11(2):15-20.

［5］Xiaodong Lu，Arash Jamalian.A new method for characterizing axis of rotation radial error motion［J］.Precision Engineering，2011，35:73-94.

［6］伍良生，杨勇，周大帅.机床主轴径向回转误差的测试与研究［J］.航空精密制造技术，2008(4):26-29.

［7］Wei G，Satoshi Kiyono，Takamitu Sugawara.High-accuracy roundness measurement by a new error separation method［J］.Precision Engineering，1997，21:123-133.

［8］Grejda Robert，Marsh Eric，Vallance Ryan.Techniques for calibrating spindleswith nanometer error motion ［J］..Precision Engineering.2005，29(1):113-123.

［9］Eric March，Jeremiah Coney，Ryan Vallance.Nanometer-Level Comparison of Three Spindle Error Motion Separation Techniques［J］.Transactions of the ASME，2006，2:180-187.

［10］罗海燕.回转误差测量新方法的研究［D］.合肥:中国科学技术大学，2008.

An Evaluation Methodology of Spindle Rotation Error based on Genetic Algorithm

GAO Hui-zhong1，LIU Fei1，LIANG Lin1，XU Guang-hua1，2，HUANG Fu-zhong3
(1.School of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，China;2.The State Key Laboratory for Manufacturing Systems Engineering，Xi’an Jiaotong University，Xi’an 710054，China)

Aiming at the evaluation of spindle rotation error，an evaluation methodology for spindle rotation error based on genetic algorithms is introduced in this paper.A calculation model with minimum envelope circle error based on genetic algorithm is established.By studying the features of precise spindle rotation error，then，taking use of genetic algorithm and minimum envelope circle method to acquire a genetic algorithm based evaluation methodology of spindle rotation error.Furthermore，experiments and applications have been shown that the evaluation methodology of spindle rotation error with minimum envelope circle based on genetic algorithm is effective.

spindle rotation error;minimum envelope circle method;genetic algorithm

TP206;TG80

A

1001-2265(2012)12-0019-04

2012-02-27;

2012-04-16

国家科技重大专项资助项目(2009ZX04001-051)

高慧中(1989—)，男，西安人，西安交通大学机械工程学院硕士研究生，主要研究方向为机械故障诊断，(E-mail)lianglin@mail.xjtu.edu.cn。

(编辑 李秀敏)