一种雷达目标的动态雷达散射截面模拟
2012-09-10韩慧奇
刘 哲 韩慧奇
(中国人民解放军63726部队,宁夏 银川 750004)
0 引言
随着隐身与反隐身技术的发展,研究目标的隐身与反隐身性能已经成为测控领域必不可少的一项工作,而研究目标的雷达散射截面(radar cross section,RCS),特别是目标的动态RCS就显得尤为重要。
目前,目标RCS的获取主要依靠理论计算、外场测试、暗室试验以及电磁仿真软件仿真等方法[1-2]。只有外场试验能测量目标的动态RCS,但外场试验所需条件苛刻,实施较为困难。文献[1]在真实环境下测量目标的动态RCS,然后利用RCS起伏模型得到RCS的预处理结果。利用起伏模型计算具有一定的不确定性。文献[2]基于暗室缩比模型条件下测得目标RCS的静态值,然后根据目标航迹得到动态RCS,其中的缩比试验需要在特定的暗室进行,并且一次试验只能对一个目标进行,具有一定的局限性。
基于以上考虑,需要寻找一种较为通用、易于实现且具有一定精度的RCS预处理方法,同时需要实现目标动态RCS的显示。雷达目标的动态RCS模拟对于研究和掌握目标的飞行特性起到了一定的作用。
1 几种相关坐标系
1.1 测量坐标系和发射坐标系
在目标跟踪的过程中,雷达工作频率较高,目标波长一般远大于雷达工作波长,在计算目标RCS时可以采用数值分析的高效算法。实现目标动态RCS模拟的关键是处理好测量坐标系和目标坐标系之间的转换关系。在目标建模中合理地选取建模坐标系,以达到简化坐标转换的目的。
在测控领域中,测量坐标系是站心坐标系的一种。它是以测控设备中心为原点的坐标系,这里我们以Ocl-xclyclzcl来表示测量坐标系,其中:Ocl位于天线回转中心;ycl轴与过原点的地球参考椭球面方向一致,并指向椭球面外;xcl轴与ycl轴垂直,由原点指向大地北;zcl轴与xcl轴和ycl轴构成右手坐标系。
发射坐标系也是站心坐标系的一种,用Ofs-xfsyfszfs来表示,其中:Ofs是目标质心在发射平面的投影点;yfs轴与发射点的铅垂线一致,指向向上;xfs轴与yfs轴垂直,由原点指向发射瞄准方向;zfs轴、xfs轴和yfs轴构成右手坐标系。
1.2 目标坐标系
本文采用O-xMByMBzMB来表示目标坐标系,其中:O位于目标质心;xMB轴与目标纵向重合,并指向目标头部;yMB轴在目标纵对称面内,垂直于xMB轴,当目标平飞时指向上方;zMB轴、xMB和yMB轴构成右手系。目标坐标系描述了空间点对目标的位置关系,除了采用直角坐标系(xMB、yMB、zMB)表示外,还可以用更加直观的极坐标表示。
本文采用极坐标表示法,其示意图如图1所示。
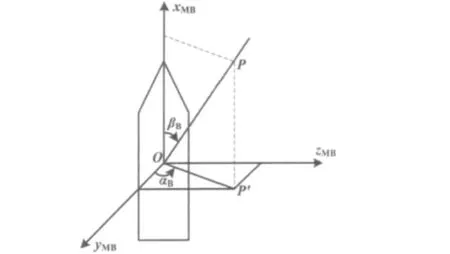
图1 目标坐标系的极坐标表示示意图Fig.1 Polar coordinate representation of the target coordinates
图1中,αB为目标径向在O-yMBzMB平面的投影OP'与yMB轴的夹角,方向由 yMB轴向 zMB轴为正;βB为目标径向与xMB轴的夹角,方向为从xMB轴向目标尾部转动。
1.3 目标姿态的表示
目标姿态由目标坐标系相对于发射坐标系的转动角描述,包括俯仰角φ、偏航角ψ和滚动角γ。俯仰角φ是指目标坐标轴纵轴在Ofs-xfsyfs平面上的投影与xfs轴的夹角,方向由xfs转向yfs;偏航角ψ是指xMB与Ofsxfsyfs平面夹角,方向从Ofs-xfsyfs平面逆时针旋转;滚动角γ是指O-xMByMB面绕xMB轴的转角,方向顺xMB轴方向右为正。其中,下标MB代表目标坐标系,下标fs表示发射坐标系。
为便于直观理解,两个坐标系和俯仰角φ、偏航角ψ、滚动角γ之间的关系如图2所示。
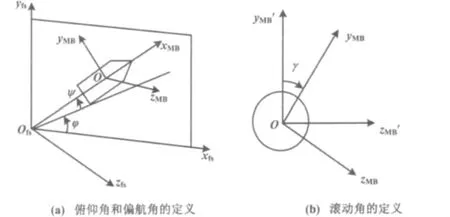
图2 目标坐标系的姿态角定义Fig.2 Definition of posture angle in target coordinates
2 坐标转换
2.1 坐标系的转换
为了计算测量坐标系在目标坐标系中的位置,先将其转换到发射坐标系下[3],即:
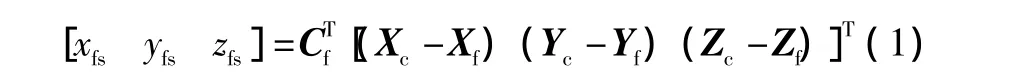
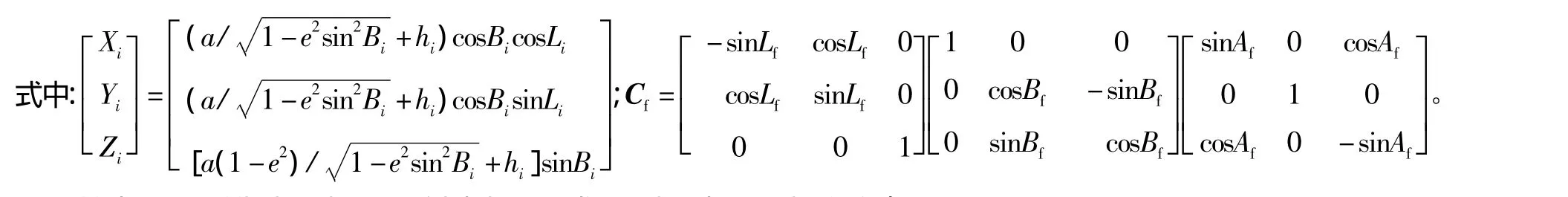
其中,i分别代表下标f(发射坐标系)或c(测量坐标系);a为参考椭球长半轴;e为第一偏心率;Lf、Bf、hf、Lc、Bc、hc分别为发射坐标系原点和测量坐标系原点的大地经纬度和高程;Af为目标姿态的发射方位角。
2.2 直角坐标表示
将发射坐标表示转换为直角坐标表示的计算公式为:
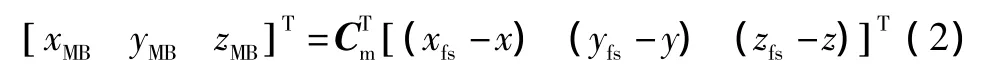
2.3 极坐标表示
测量坐标系的极坐标示意图如图3所示。
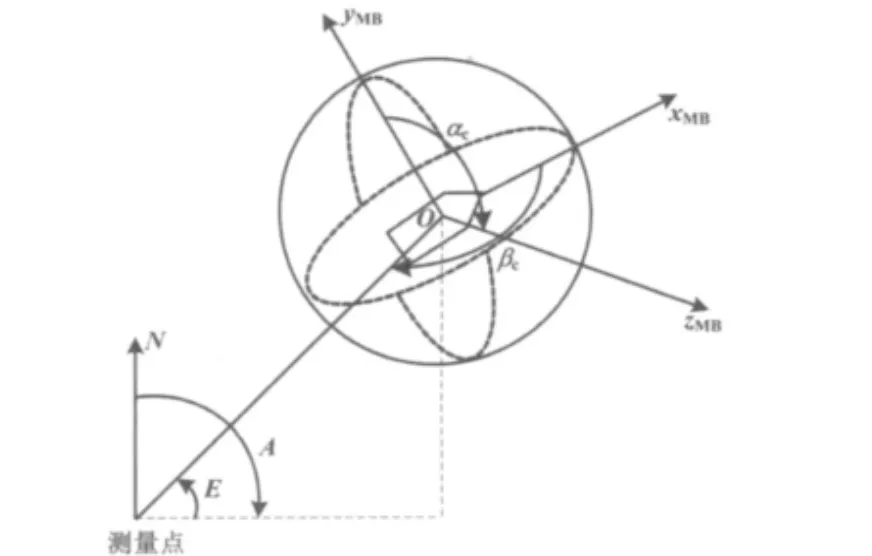
图3 测量坐标系的极坐标表示示意图Fig.3 Polar coordinate representation of the measurement coordinates
将直角坐标表示转换为极坐标表示的计算公式为:
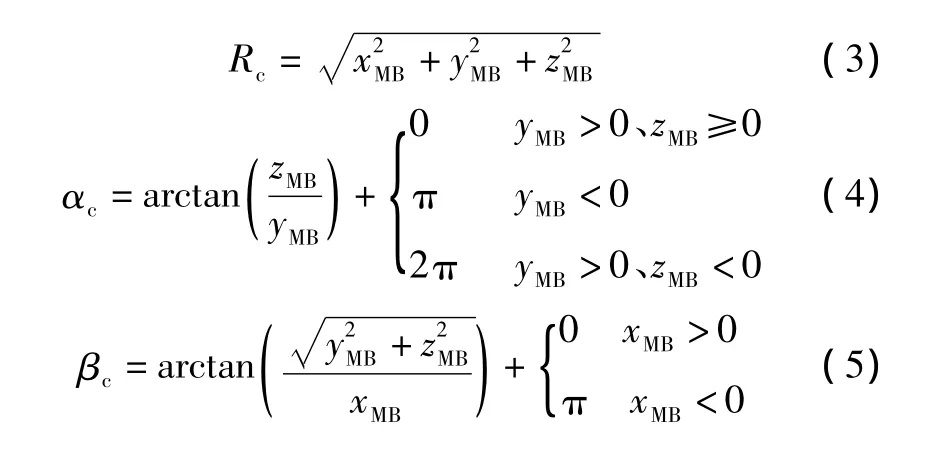
3 快速多极子算法原理
快速多极子方法是将积分方程中的格林函数进行加法处理,在角谱空间中用平面波进行算子对角化,将计算问题转化为稀疏阵与矢量的相乘。算法的核心思想是分组。
任意两个子散射体间的互耦根据所在组的位置关系,采用不同的算法来减少计算量。相邻组直接进行数值计算,非相邻组采用聚合、转移、配置的步骤计算。
对于场点组,先将各个非相邻组的所有子散射体产生的贡献聚合到组中心,再将这些贡献转移到给定场点组的中心,然后将散射体产生的贡献聚合到组中心,接着将这些贡献转移到给定场点组的中心,最后将由中心配置到组内各个子散射体。
若散射体表面有N个子散射体,当直接计算互耦时计算量为O(N2),而采用快速多极子计算量只为O(N1.5),大大减少了计算量[4]。
矩阵与矢量相乘的快速多极子表达公式为[5]:
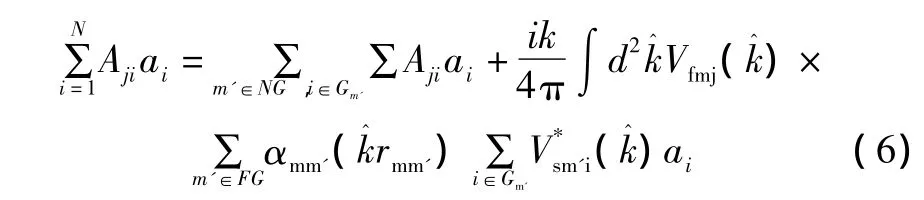
式中:j∈Gm;αi为第i个源子散射体的电流幅度;NG为附近组的贡献;FG为非附近组的贡献;Vsm'i(k^)、Vfmj(k^)αmm'为聚合因子、转移配置因子。
对于电大尺寸目标的散射问题,其未知量数目N>>1,应用多层快速多极子法(multilevel fast multipole method,MLFMM)可以获得更高的效率。基于多层级结构的思想,提出了多层快速多极子方法。对于N体互耦,多层快速多极子方法采用多层分区计算,附近区强耦合量直接计算,非附近区耦合量用多层快速多极子方法实现。
多层分区计算的特点是逐层聚合、逐层转移、逐层配置、嵌套递推。从实质上讲,多层快速多极子方法是快速多极子方法的多层扩展,多层快速多极子方法除了聚合、转移、配置的相似步骤外,还有父层、子层间的递推计算[6-7]。
采用多层快速多极子法,对文献[7]中的某椎柱几何模型进行建模仿真,模型坐标系z轴正向指向椎尖,圆柱半径为80 mm、柱高260 mm、椎半角为11°、入射频率为5 GHz、入射角度 φ=90°,得到单站RCS的变化曲线如图4所示。
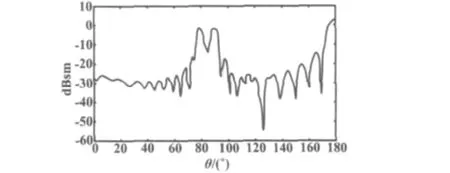
图4 RCS变化曲线Fig.4 RCS variation curve
由图4可以看出,RCS曲线与文献[7]中验证的结果基本吻合,说明此方法的有效性和正确性,满足工程实际需要。
4 动态RCS仿真程序流程
目标动态RCS仿真程序流程如图5所示。
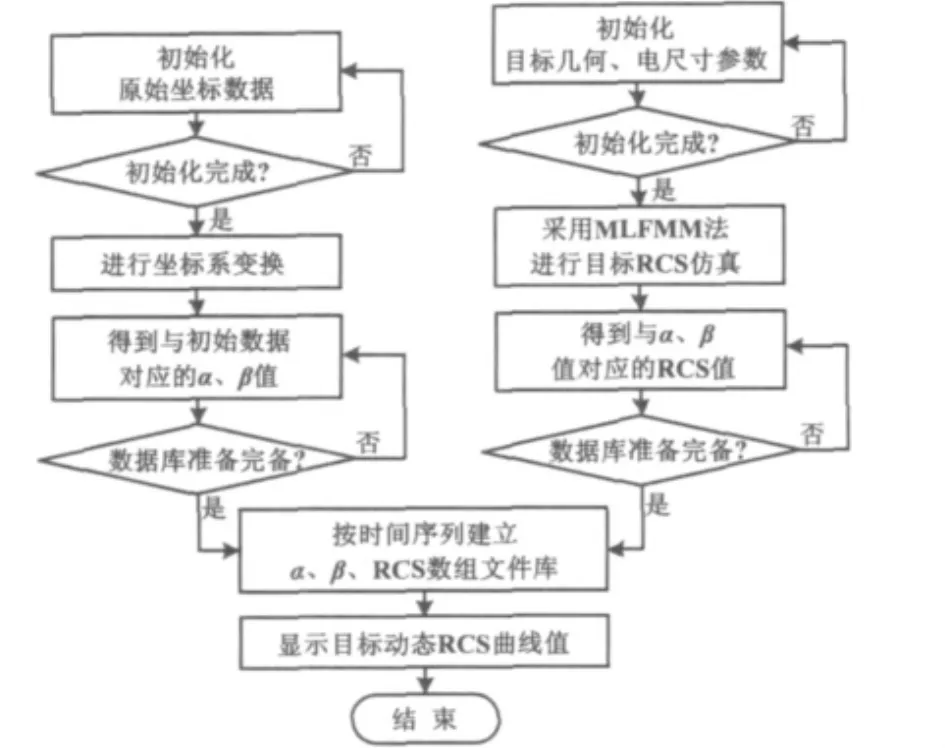
图5 目标动态RCS仿真程序流程图Fig.5 Flowchart of the target dynamic RCS simulation program
根据以上分析,本文中实现目标动态RCS模拟的具体步骤如下。
①利用几种坐标变换原理,编程实现初始航迹对应的目标坐标系下的(αc,βc)数组对,并形成数据库等待调用;
②根据多层快速多极子算法,对目标在建模的基础上进行远场仿真,建模坐标系的建立与目标系一致,由此得到与(αc,βc)数组对具有一一对应关系的RCS数据库文件;
③按照目标航迹的飞行时间将目标仿真库的RCS值以动态时间序列显示,模拟目标动态RCS。
根据以上步骤得到文献[7]中的某椎柱几何模型单站动态RCS模拟曲线如图6所示。
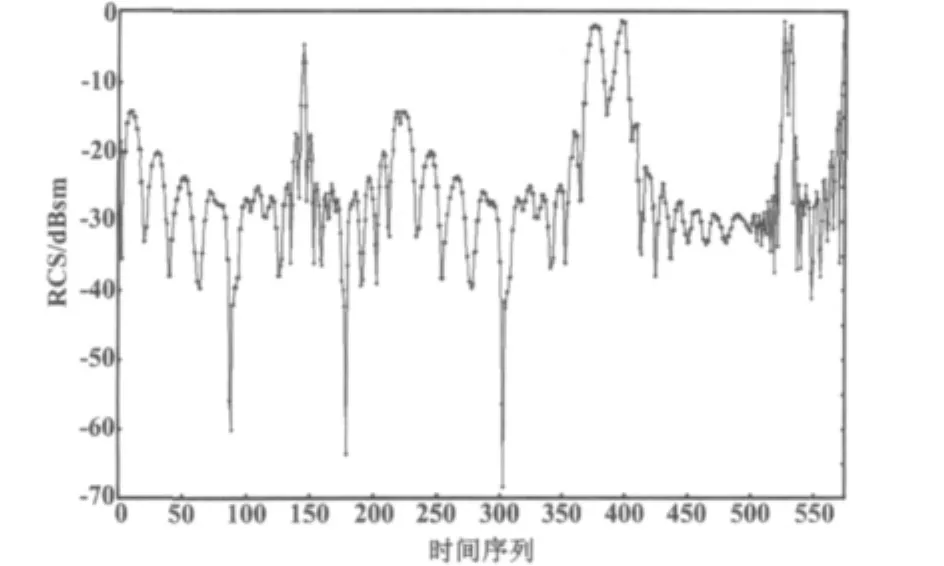
图6 目标单站动态RCS模拟曲线图Fig.6 Curve of target single station dynamic RCS simulation
从图6可以看出,400序列RCS值达到最大,525序列以后有几个波动较大的峰值,并且RCS值在这段序列内变化剧烈。这也恰好说明这段时间目标姿态调整频繁,与航迹数据分析基本一致。从工程角度讲,这种模拟具有大致掌握目标飞行特性的实际意义[8]。
5 结束语
本文采用多层快速多极子算法,通过对坐标系的恰当选取和坐标系转换,编程实现了对目标动态RCS的模拟,并通过实例说明了这种模拟对于实际工程的意义。目前,采用这种方法模拟显示目标动态RCS的程序已经应用在某设备中,并能提供一定意义下的目标飞行特性信息。
[1]刘英芝,曾勇虎,汪连栋,等.动态雷达目标仿真中目标姿态角的计算[J].电光与控制,2007,14(1):38 -41.
[2]张居凤,冯德军,王雪松,等.雷达目标动态RCS仿真研究[J].系统仿真学报,2005,17(4):834 -837.
[3]黄学德.导弹测控系统[M].北京:国防工业出版社,2000.
[4]John H M ,Kurtis D F.数值方法[M].周璐,陈渝,钱方,等,译.北京:电子工业出版社,2002.
[5]聂在平.目标与环境电磁散射特性建模——理论、方法与实现(基础篇)[M].北京:国防工业出版社,2009.
[6]胡俊,聂在平,王军,等.基于多层快速多极子方法的三维目标RCS高效数值求解技术[J].电波科学学报,2004,19(10):92 -94.
[7] 王超.NURBS曲面 RCS算法研究[D].西安:西北工业大学,2004.
[8]吉雅娴.ESD与TPS之间的数据通信[J].石油化工自动化,2008(3):54-56.
