全流程污水生化处理过程的仿真设计

金 辉 黄明忠 潘多涛 袁德成

(沈阳化工大学辽宁省化工过程控制技术重点实验室，辽宁 沈阳 110142)

0 引言

污水生化处理厂具有保护环境的功能，但其副产品——过剩污泥若不能有效利用，也将造成严重的二次污染［1］。随着全球能源问题的日趋突出，如何捕获蕴含在污水处理厂活性污泥新陈代谢中的潜在能量开始受到人们的关注［2－3］。为了进一步改善水质，降低剩余污泥量，实现全流程、长周期的性能评价，国际水协会(International Association of Water，IWA)推出了2号基准仿真模型(Benchmark simulation model No.2，BSM2)［4］。

本文根据IWA工作组关于典型污水生化处理过程的组成协议BSM2［5］，采用 Matlab与 C语言混合编程的方法，开发了面向全流程的污水处理仿真平台。经过相关的稳态计算和溶解氧控制测试，得到的计算结果与工作组发布的最终测试数据一致。该平台可用于全流程污水处理厂的模拟计算。

1 国际评价基准Benchmark

1.1 Benchmark 工厂构成

Benchmark工厂的入水平均流量为20 648.26 m3/d，入水平均化学需氧量(COD)为592.53 g/m3，水力停留时间为22 h。工厂除了包括5个生化反应器和1个二沉池外，还包括1个初沉池、1个污泥浓缩机和1个厌氧消化池，同时还增加了1个脱水单元。基于BSM2的污水处理厂构成如图1所示，其中活性污泥反应器和二沉池的计算与BSM1保持一致。

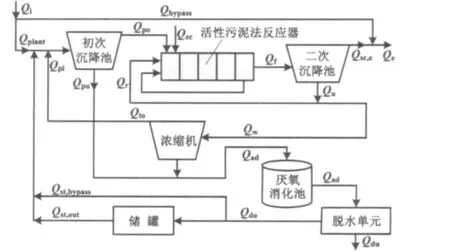
图1 污水处理厂构成图Fig.1 Composition of wastewater treatment plant

1.2 模拟模型

由于BSM2中生化反应器和二沉池部分的模拟模型与 BSM1相同［6－8］，故这里不再作详细说明。下面针对其余部分的模拟模型进行一一介绍。

1.2.1 厌氧消化模型

厌氧消化1号模型(anaerobic digestion model No.1，ADM1)是一个结构化模型，它对厌氧系统内的生化过程和物化过程进行了详细分析。它采用微分代数方程组(differential algebraic equations，DAE)来描述生化和物化过程。该过程涉及7个微生物种群，方程组包括26个动态浓度变量、19个生化动力学过程、3个气液传质过程和8个隐式代数变量。

ADM1将厌氧消化过程中的生化反应具体细化为19个子过程。生化过程的反应速率方程采用形如Monod方程的基质降解动力学方程来描述，而不是采用ASM系列模型中类似的微生物增殖动力学方程来描述，这是ADM和ASM模型最主要的区别之一。

厌氧消化1号模型共有26个组分，包括14个可溶性组分和12个不溶性组分。对于每一个组分，根据物料平衡原则，可以得到以下微分方程:

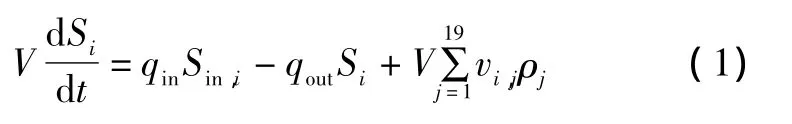
式中:V为液相或气相的体积;Si为组分i的浓度;t为时间;qin为组分i流入体系的流量;qout为组分i流出体系的流量;vi，j为组分i对应于过程 j的速率系数;ρj为过程j的反应速率。此外，ADM1认为在厌氧消化过程中主要存在pH抑制、氢抑制和游离氨抑制这3种抑制作用。

物化过程是厌氧消化体系的重要组成部分。ADM1将厌氧消化系统中的物化过程分为液相中的酸碱离解平衡和气液两相间的传质过程。

液相中的酸碱离解平衡主要涉及氢离子、氢氧根离子、有机酸根、氨根和碳酸氢根等的离解平衡。由于这些化学过程的反应速率非常快，可以直接采用稳态的平衡方程式来表达。

ADM1认为厌氧消化过程所产生的沼气主要有CH4、H2、CO2等3种气体组分，传质阻力主要存在于液相。因此，ADM1在双膜理论的基础上，采用Stumm和Mor2gan推导的公式，对气液两相间的传质过程进行描述。

1.2.2 初次沉降池的建模

在污水处理厂中，初次沉降池的作用是去除污水原液中的颗粒物质。初次沉降池的工作效率直接影响活性污泥处理单元的处理效果。将初次沉降池描述为一个混合储罐［9－10］，储罐的出水可分为初次沉降池流出量和初次污泥两部分，其中流出量和初次污泥的组分与活性污泥部分相同。

1.2.3 浓缩机和脱水单元的建模

浓缩机的作用是将从二次沉降池中的污泥进行浓缩，并将浓缩后的污泥向上输入给初沉池，向下进入消化池。

如果浓缩因子fthick＞1，下溢变量计算为:①任意颗粒组分，Ztu=Ztufthick;②对于任意可溶性组分，Ztu=Zu;③下溢流量Qtu=Qwfqtu。

此时，上溢变量计算为:①对于任意颗粒组分，Zto=Zufthin;②对于任意可溶性组分，Zto=Zu;③上溢流量Qtu=Qw(1－fqtu)。

如果浓缩因子fthick＜1，则表示浓缩过程存在错误。

脱水单元的作用是将来自消化池的消化污泥进行浓缩。经过浓缩处理的废水回流到初次沉降池的入口处。由于脱水单元的模型与浓缩机建模机理类似，这里不再累述。

1.3 模型接口

BSM2将液相流和污泥流相结合，实现了全流程污水处理过程。液相流部分采用ASM1模型进行模拟，污泥流部分则使用ADM1模型。由于ASM1和ADM1中的状态变量不同，因此，在对这两个过程进行合并的过程中，定义模型接口和对状态变量进行转换显得十分必要［6，11］。

模型接口定义的基本原则是转换前后质量守恒。对于ASM1-ADM1接口来说，在转换的过程中，应使总COD(CODt)和总TKN(TKNt)保持质量守恒。其中总COD表示有机状态变量组成的复合变量，总TKN是指包括氨氮在内的有机氮复合测量值。

ASM1-ADM1接口的目的是将与ASM1对应的活性污泥状态变量转化为与ADM1对应的厌氧消化状态变量。ASM1-ADM1接口转换的基本思想是使复合组分Xc(包括Saa、Si、Xi)关于可用氮和 COD达到最小。这里使用状态变量的自由度来达到平衡，即采用状态变量关于碳或氮的自由度来达到平衡。在这种转换方法中，由于假设Ssu(无机氮)、Xch(糖类)和Xli(脂类)不含有氮，因此，将Ssu、Xch和Xli作为含碳自由度。类似地，将Sin作为含氮自由度。

ADM1-ASM1的作用是将消化池出口处的任意状态变量转换为用于脱水单元的状态变量。由ADM1状态变量转换到ASM1状态变量这一过程相对简单，这种转换过程的目的是使Xs、Ss、Si和Xi关于可用COD最小，Xnd和Snd含氮量达到最小。

1.4 输入污水的组成

BSM1分别针对晴天、雨天和暴雨天气设计了3个污水输入文件。对于BSM2，输入文件并不是依据预先定义好的数据文件来确定，而是根据模型进行设计。在BSM2中，对象性能的评价周期为364 d。在对性能评价之前，应先确定动态镇定周期。动态镇定周期为245 d。因此，BSM2的输入污水文件由609 d的动态数据组成。

1.5 性能评价指标

与一般的工业生产过程相比，污水处理厂的运行具有特殊性。它的最终“产品”首先必须遵守环保法规强制性的排放要求，然后才考虑工艺目标和控制目标的实现。如何将上述操作要求分解统一到控制系统的设计和实施中，目前仍然没有完全解决。评价运行效果需要综合以下几个指标。

①常规的控制系统指标:如绝对误差积分(integral of absolute error，IAE)、积分平方差(integral square error，ISE)、最大偏差、方差、越界的次数和持续时间等。

② 出水限制指标:总氮浓度 Ntot，e＜18 gN/m3、化学需氧量 CODtot，e＜100 gCOD/m3、氨氮浓度 SNH，e＜ gN/m3、固体悬浮物浓度TSS＜30 gS/m3、生物需氧量浓度BOD5，e＜ 10 gBOD/m3。

③出水质量指标(EQI):EQI是衡量主要污染物对受纳水体污染程度的一个指标。观测期内(从第245 d开始到第609 d)的EQI表达式为:

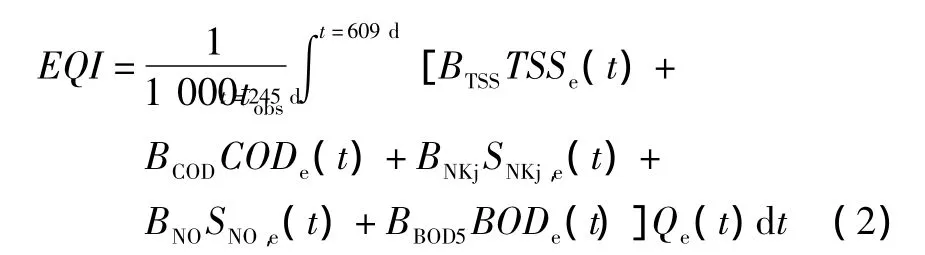
总凯氏氮浓度:

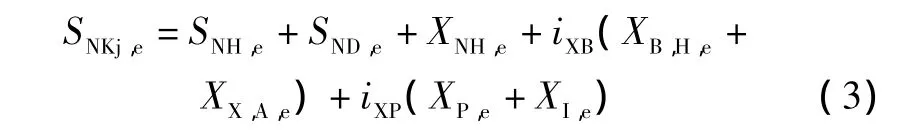
总固体物浓度:

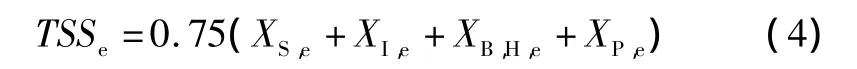
5天生化需氧量:

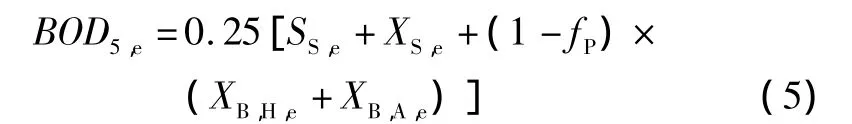
化学需氧量:

④经济指标:经济指标主要从污泥产量(SP)、曝气风机能耗(AE)和泵机能耗(PE)这3方面进行考虑。

污泥产量(SP)主要根据研究时间内(从第245 d开始到第609 d)排放的污泥量以及系统积累的污泥量来计算:

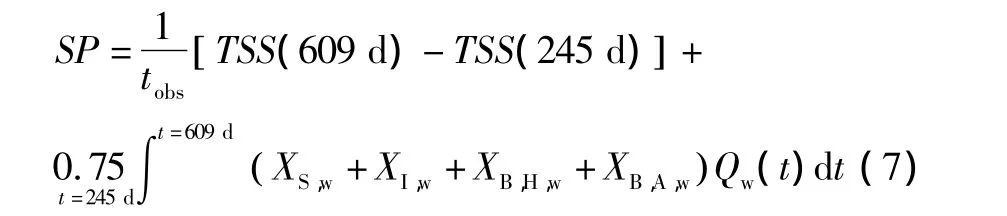
此外，系统的总污泥产量是指处置污泥与系统流失污泥的总和，具体计算方法如下:

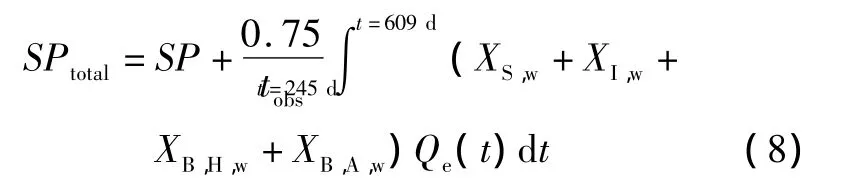
在污水处理的成本核算中，约40% ～60%的电能消耗在泵和风机上，其节能控制日益受到重视。其中曝气风机能耗定义为:

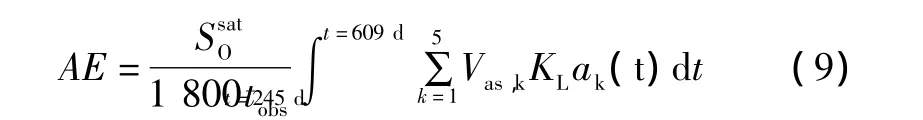
泵机能耗的计算表达式为:

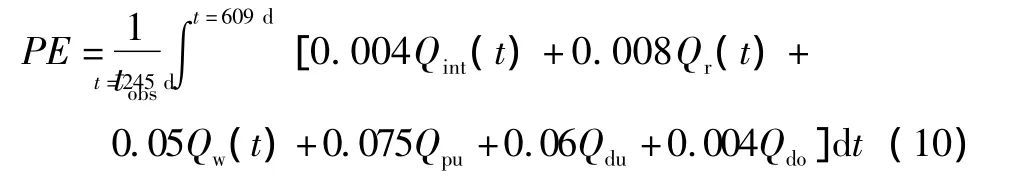
2 数值计算结果

本文根据BSM2协议，开发了基于Matlab/Simulink与C语言混合编程的仿真程序。主程序采用Matlab编写，模型与模型之间的接口均采用C语言编程。整个污水处理厂的模型通过Simulink进行搭建，在开源Linux环境中运行。

为验证仿真程序计算的稳定性和一致性，首先在不加控制作用的情况下，对开环性能进行了仿真。仿真结果如表1所示。

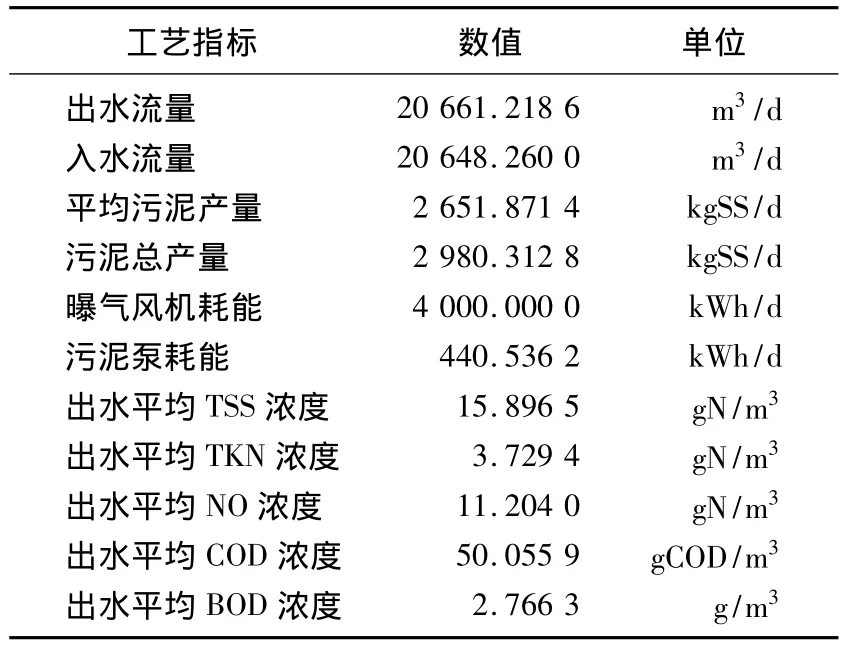
表1 仿真结果Tab.1 Simulation results

由表1可知，系统在开环情况下具有较好的稳定性。被控变量4号反应器的溶解氧浓度和控制误差曲线如图2所示。

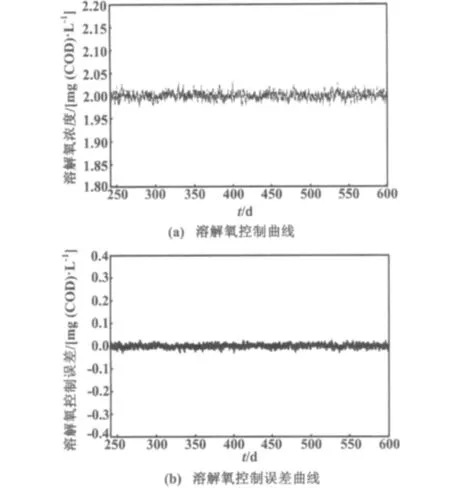
图2 溶解氧控制和控制误差曲线Fig.2 The dissolved oxygen control and control error curves

被控变量的常规性能指标如表2所示。

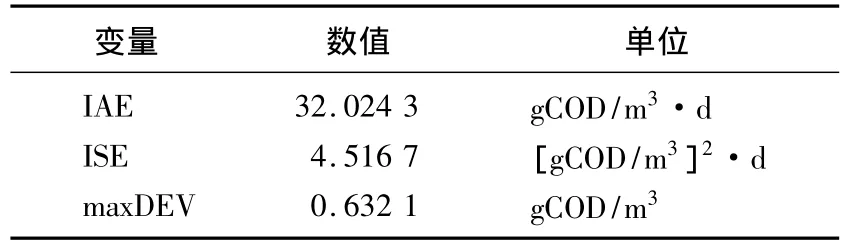
表2 常规性能指标Tab.2 Common performance indexes

出水水质指标如表3所示。

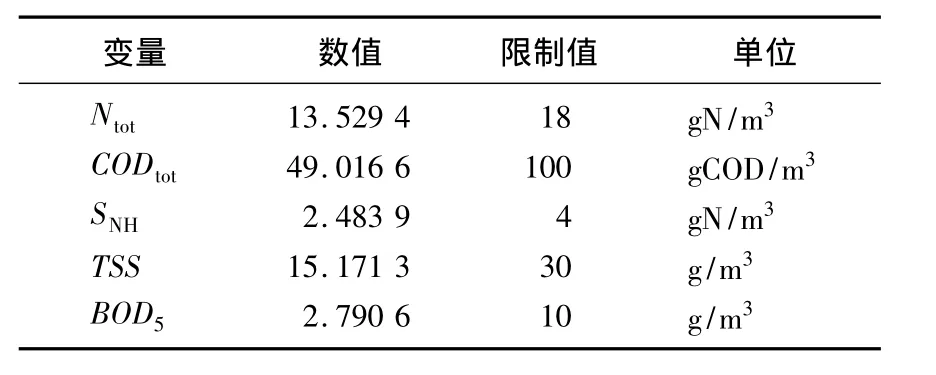
表3 出水水质指标Tab.3 Effluent water-quality indexes

根据出水水质，可得出水质量指标如图3所示。

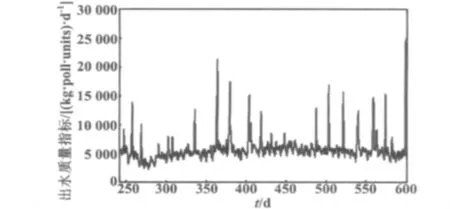
图3 出水质量指标Fig.3 Effluent quality index

AE、PE、SP和SPtotal这几项经济指标的平均值如表4所示。

表4 经济指标Tab.4 Economic indexes

若将4号反应器溶解氧浓度(SO4)设置值改为2.5 mg(COD)/L，所得溶解氧浓度变化和控制误差曲线如图4所示，进一步说明了仿真平台的有效性和稳定性。

图4 改变后的溶解氧控制和控制误差曲线Fig.4 The dissolved oxygen control and control error curves while changing set point

3 结束语

全流程污水处理过程不仅要保证出水水质达到环保排放标准，同时也必须考虑剩余污泥的处置和成本，这是污水处理工业的发展方向。为此，本文开发了基于BSM2协议的全流程污水生化处理过程标准仿真平台。利用该仿真软件可完成:①稳态初值计算和动态特性模拟;②基于三类性能指标的最佳工艺选择和设计;③先进控制策略的评价等任务。基于BSM2污水处理过程的研究还处于初级阶段，仍有大量问题尚未解决，仍需研究人员进行更深入的研究。

［1］ Volcke E I P.Modeling，analysis and control of partial nitritation in a SHARON reactor［D］.Belgium:Ghent University，2006.

［2］ Kargbo D M.Biodiesel production from municipal sewage sludges［J］.Energy Fuels，2010，24(1):2791 －2794.

［3］ Pittman J K，Dean A P，Osundeko O.The potential of sustainable algal biofuel production using wastewater resources［J］.Bioresource Technology，2011，102(1):17 －25.

［4］ Jeppsson U，Rosen C，Alex J，et al.Towards a benchmark simulation model for plant-wide control strategy performance evaluation of WWTPs［J］.Water Science and Technology，2006，51(1):287 －295.

［5］ Henze M.COST 624:Optimal management of wastewater systems［EB/OL］.［2006 －08 －12］.http://www.ensic.inpl-nancy.fr/COSTWWTP.

［6］ Batstone D J，Keller J，Angelidaki I，et al.Anaerobic digestion model No.1［M］.London:IWA Publishing，2002.

［7］ Henze M，Gujer W，Mino T，et al.Activated sludge models ASM1，ASM2，ASM2d，ASM3［R］.IWA Scientific and Technical Reports，London，2000.

［8］ Takács I，Patry G.A dynamic model of the clarification-thickening process［J］.Water Research，1991，25(10):1263 －1271.

［9］ Otterpohl R，Freund M.Dynamic models for clarifiers of activated sludge plants with dry and wet weather flows［J］.Water Science and Technology，1992，26(5):1391 －1400.

［10］Otterpohl R，Raak M，Rolfs T.A mathematical model for the efficiency of the primary clarification［C］∥Proceedings of IAWQ 17th Biennial International Conference，Budapest，Hungary，1994.

［11］Copp J B，Jeppsson U，Rosen C.Towards an ASM1-ADM1 state variable interface for plant-wide wastewater treatment modeling［C］∥Water Environment Federation Conference，WEFTEC 2003，Los Angeles，California，2003.