四边简支条件下正交各向异性蜂窝夹层板的固有特性分析

王盛春，邓兆祥，沈卫东，王 攀，曹友强

(1.重庆大学 机械传动国家重点实验室，重庆 400030;2.重庆通信学院 军用特种电源军队重点实验室，重庆 400035)

蜂窝夹层作为一种特殊的复合材料结构，具有高比刚度、高比强度、性能可设计等优点，在航天、航空、高速交通运输工具和现代结构工程等许多领域广泛应用，如制造飞行器表面蒙皮、客机机舱地板、高速列车车厢、汽车门板等。研究蜂窝夹层板的弯曲振动特性具有十分重要的意义。在过去几十年间，国内外学者运用解析方法和数值方法从各种角度对蜂窝夹层板的振动特性进行研究。文献［1－3］运用经典叠层板理论研究了复合材料夹层结构的振动问题。Monforton［4］和Zhou HB等［5］分别用有限元和样条有限点法研究了正交各向异性夹层板的弯曲和振动问题。Raville等［6］通过实验测定了夹层板的固有频率。文献［7］给出了包含两个未知函数的各向同性夹层板的自由振动方程及四边简支矩形夹层板的固有频率精确解。石亦平等［8］研究了面板、胶层及蜂窝芯各项参数对蜂窝夹层板固有频率的影响，但在理论推导中将厚度较大的夹层板等效为符合Kirchhoff直法线假定的实心薄板，未考虑蜂窝芯层弯曲变形的影响。李永强等［9］应用三阶剪切板理论研究了蜂窝夹层板板厚、芯层厚度及胞元角度对夹层板固有频率的影响，但在设计参数对固有频率影响机制的物理解释上显得有些不足。Gibson等［10］给出了蜂窝芯层的等效参数公式，但由于未考虑胞元壁板的伸缩变形，限制了其在蜂窝夹层结构分析中的应用。富明慧等［11］对Gibson公式进行了修正。

从以上分析可知，虽然进行了诸多研究，然而由于涉及的控制方程非常复杂，现有关于蜂窝夹层板固有频率的准确解主要是各向同性材料的夹层板壳，而且蜂窝夹层板各项设计参数对其振动特性的影响问题，现有研究成果仍不能满足工程实践的需要。本文给出了一种将正交各向异性蜂窝夹层板的控制方程组化为仅含一个位移函数的单一方程的方法，从而获得了在四边简支边界条件下其自由振动固有频率的精确解，并对夹层板的各项设计参数对其固有频率的影响进行了深入细致的讨论，进而筛选出了夹层板固有频率的主要影响参数。该研究结果对蜂窝夹层板的结构设计和工程应用具有指导意义。

1 夹层板自由弯曲振动控制方程

图1为一块由对称上、下面板和蜂窝芯所组成的正交各向异性矩形蜂窝夹层板，边长为a和b，夹层板总厚度为H，芯层厚度为h，面板厚度为t。坐标平面x－y与夹层板中面在同一水平面内，且材料主轴与x轴和y轴方向一致。图2为夹层板芯层的六边形蜂格结构。

图1 正交各向异性蜂窝夹层板Fig.1 Schematic of the geometry of rectangular orthotropic honeycomb sandwich panel

图2 芯层的六边形蜂格结构Fig.2 Schematic of the regular hexagon cell of the honeycomb core

根据Reissner-Mindlin的夹层板剪切理论和蜂窝芯层的“反平面”理论［2］，提出以下基本假定:

(1)面板厚度与整个夹层板厚度相比很小，可做薄膜处理，即面板只承受面内力 σx，σy，τxy，且沿其厚度均匀分布。

(2)蜂窝芯层材质较软，仅能抵抗横向剪切变形，且其横向剪切应力τxz，τyz沿蜂窝芯层厚度方向不变，忽略芯层中平行于x－y平面的应力分量，即在芯层中σx=σy=τxy=0。

(3)弯曲前垂直于夹层板中面的法线弯曲变形后依然保持直线，但不垂直于夹层板中面，直法线假设仅适用于薄面板。

(4)沿夹层板厚度方向无正应变，即在面板和芯层中σz=0。

1.1 夹层板自由振动控制方程组

考虑材料主轴与x轴和y轴一致的情况，对于上、下面板厚度和材料均相同的情况，有:

式中，Mx、My和Mxy为夹层板的内力矩，Qxz、Qyz为夹层板的横向剪切力，w为夹层板的横向挠度，ψx，ψy分别为变形前垂直于夹层板中面xoy的直线段在x－z平面及y－z平面内的转角，Dij(i，j=11，12，22，66)为夹层板的弯曲刚度，C13、C23为芯层的剪切刚度，C13=G13h(1+t/h)2，C23=G23h(1+t/h)2，其中G13、G23分别为芯层在x－z和y－z平面内的剪切模量。

由于只关心夹层板的自由弯曲振动，故面内惯性力可忽略不计，由此得平衡方程:

式中ρ为夹层板的面密度，w为夹层板在横向载荷作用下的挠度。

将式(1)和式(2)代入式(3)－式(5)，得到正交各向异性蜂窝夹层板的横向自由弯曲振动控制方程组:

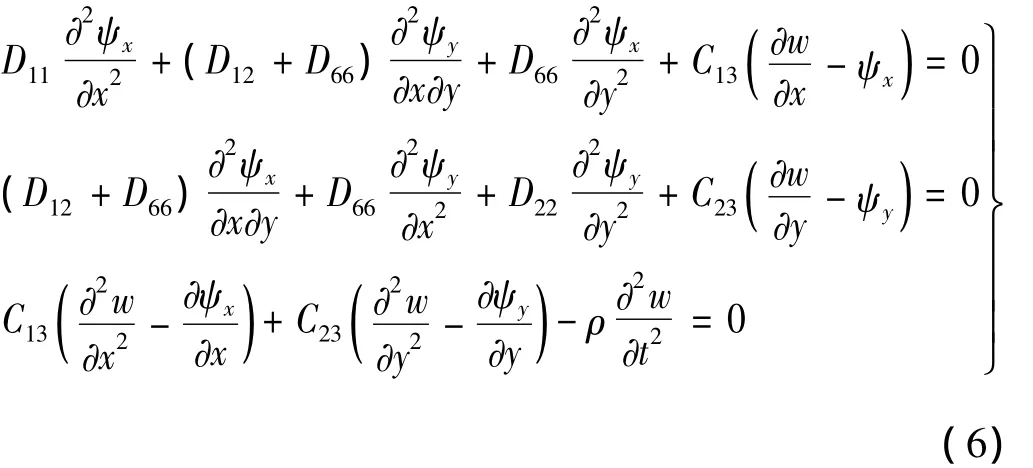
在上述控制方程组中含有3个广义位移w，ψx和ψy，求解方程组非常困难。下面将通过引入位移函数ω，用来表示3个广义位移，从而将控制方程组简化为仅含有位移函数ω的单一方程。

1.2 单一位移函数控制方程的推导

方程组(6)的前两式合并写成如下形式:

其中:

引入位移函数ω，并令:

则有:

即:

结合式(6)和式(8)－式(11)，广义位移w，ψx和ψy用位移函数ω表示为:

将式(12)代入方程组(6)的第一式，则可得仅含有位移函数ω的正交各向异性蜂窝夹层板自由弯曲振动控制方程:

2 四边简支蜂窝夹层板的固有频率

根据式(13)可导出任意边界条件下的固有频率，为简单起见，此处只讨论四边简支边界条件，即:

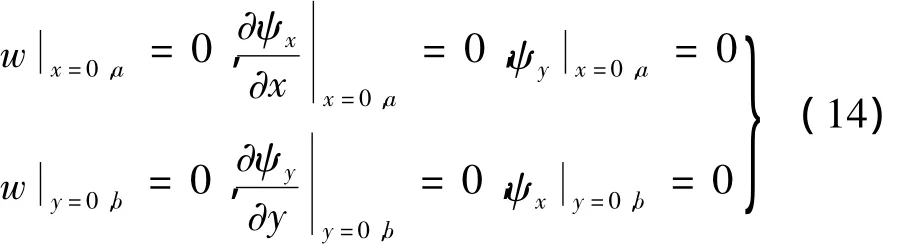
由式(12)，位移函数ω满足边界条件:

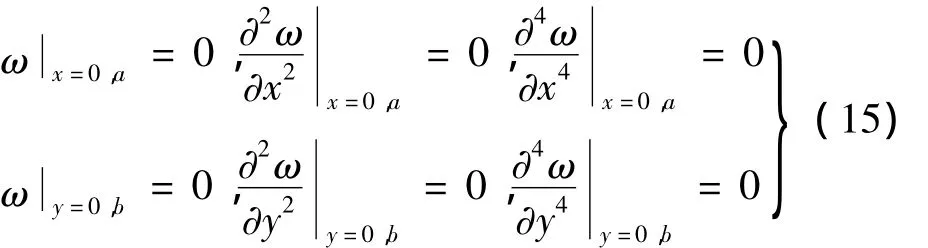
显然，满足上述边界条件的控制方程的解具有如下形式

式中Ω为夹层板的固有频率，km=mπ/a，kn=nπ/b。

将式(16)代入控制方程(13)中，可得:

对于确定的模态序数(m，n)，由式(17)即可得到夹层板的固有频率Ω。

3 数值结果和讨论

3.1 模型验证

为检验本文方法的精确程度，取与文献［12］相同的夹层板材料参数(如表1)。将式(17)的固有频率计算结果与具有相同结构和材料参数夹层板固有频率的实验值与有限元法、样条有限点法及高阶剪切理论的计算结果进行比较，结果见表2。

表1 夹层板材料参数Tab.1 Mechanical and geometrical properties of the panel

从表2可知，用本文方法计算得到的正交各向异性蜂窝夹层板固有频率与数值结果和实验结果具有很好的一致性，说明该方法是正确的。

表2 正交各向异性蜂窝夹层板固有频率比较Tab.2 Natural frequencies of the orthotropic honeycomb sandwich panel

3.2 夹层板设计参数对固有频率的影响

将蜂窝夹层板看作由上面板、芯层和下面板组成的三层层合板，层合板为正交各向异性，每一层的应力－应变关系满足广义胡克定律:

平面刚度矩阵［Q］各元素为:

芯层的等效弹性参数按修正后的Gibson公式计算［11］:

式中Es为蜂窝材料的杨氏模量，d为蜂格壁厚，l为蜂格边长。

层合板的弯曲刚度可用下式计算:

夹层板的等效密度为

3.2.1 面板厚度与夹层板厚度比t/H对夹层板固有频率的影响

取蜂窝夹层板的边长a=b=1.0 m，蜂格为正六边形蜂窝结构，蜂格边长l=1.833×10－3m，蜂格壁厚d=2.54×10－5m，面板材料为硬质铝，面板弹性参数为E=69.0 GPa，泊松比 μ =0.33，面板密度 ρf=2 700 kg/m。由于各阶固有频率的变化是成比例的，分析结果适用于每一阶固有频率。不失一般性，此处仅研究面板、芯层各项结构和材料设计参数对夹层板第一阶固有频率的影响。

图3所示为t/H值在［0.05，0.15］区间内变化时对不同厚度夹层板固有频率的影响关系曲线。芯层厚度h随着t和H的变化做相应的调整。

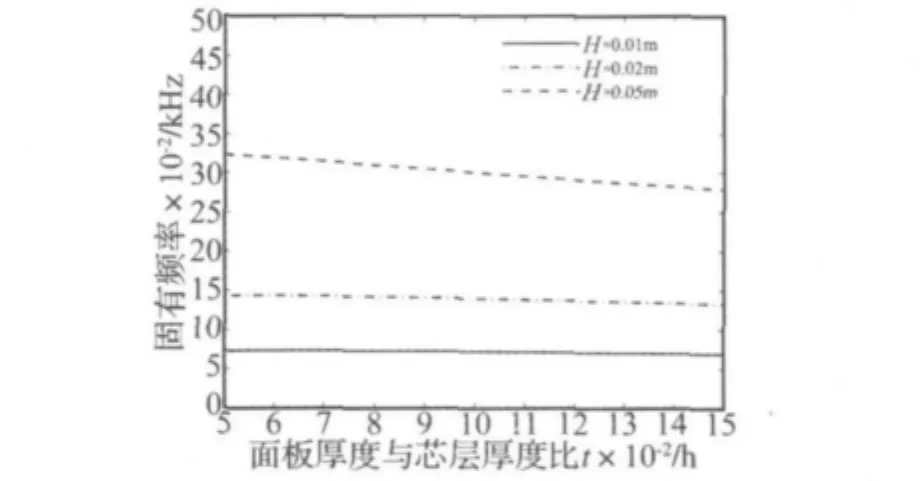
图3 面板厚度对蜂窝夹层板固有频率的影响关系曲线Fig.3 Effects of thickness ratio of face sheet and core on natural frequency

由图3和式(21)可知，t增大虽然引起夹层板质量增加且面板弯曲刚度有增大的趋势，但在夹层板厚度H不变的情况下面板厚度增大引起芯层厚度h减小，此时芯层作为上下面板间隔对夹层板整体弯曲刚度增强作用减弱，由此导致夹层板整体弯曲刚度降低。在上述两种作用的共同调控下，夹层板固有频率随面板与夹层板厚度比的增大呈略微下降的趋势。

3.2.2 面板纵向杨氏模量对夹层板固有频率的影响

蜂窝夹层板的边长、蜂格尺寸及弹性参数同3.2.1。图4 为t/H=0.10，面板纵向杨氏模量在 40 ～200 GPa范围内变化时对不同厚度夹层板固有频率的影响关系曲线。

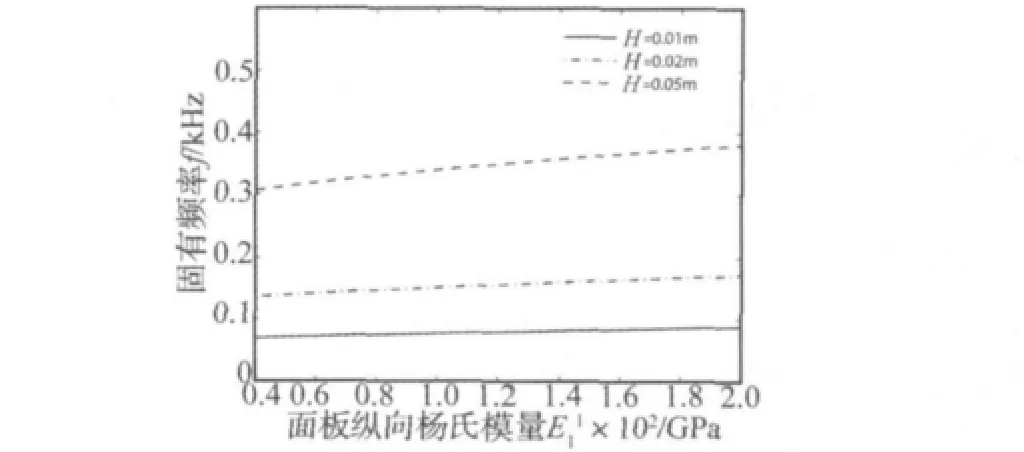
图4 面板弹性参数对蜂窝夹层板固有频率影响关系曲线Fig.4 Effects of Young’s modulus of face sheets on natural frequency

由图4和式(20)可知，在t/H保持不变的条件下，面板纵向杨氏模量E(1.3)1的增加引起夹层板整体弯曲刚度的增加，因此不同厚度的夹层板固有频率圴呈逐渐上升的变化趋势，且上升的速度随夹层板厚度的增加而加大。

3.2.3 蜂格参数对夹层板固有频率的影响

蜂窝夹层板的边长及弹性参数同3.2.1。图5(a)、图5(b)分别为t/H=0.10，蜂格壁厚d在 1.0 ×10－5m －10.0 ×10－5m(l取固定值)、蜂格边长l在2.0×10－3m －20.0 ×10－3m(d取固定值)范围内变化时对不同厚度夹层板固有频率的影响关系曲线。

图5 蜂格参数对蜂窝夹层板固有频率影响关系曲线Fig.5 Effects of cell parameters of honeycomb core on natural frequency

由图5(a)和式(19)－式(21)可知，当夹层板厚度较小(H≤0.02 m)时，蜂格壁厚d的增加引起芯层杨氏模量的增加进而增大了夹层板的弯曲刚度，但同时d的增加引起夹层板等效密度的增加，这两种作用的交互作用使夹层板固有频率随d的增加呈略微下降的变化趋势;当夹层板厚度较大(H=0.05 m)、d很小(d＜3×10－5m)时，d对夹层板弯曲刚度的增强作用较为明显，而对等效密度的减小作用较为微弱，此时固有频率随d的增加先上升再下降的变化趋势。

由图5(b)可知，蜂格边长l的增加会同时造成芯层杨氏模量、夹层板整体弯曲刚度和等效密度的降低，而对夹层板整体弯曲刚度的调控作用更加明显，因此夹层板固有频率随l的增加呈略微下降的变化趋势;当夹层板厚度较大(H=0.05 m)、l很小(l＜5 ×10－3m)时，增大l对夹层板整体弯曲刚度的减弱作用更为显著，此时固有频率随l增加的下降速度较大。

3.2.4 蜂窝材料杨氏模量对夹层板固有频率的影响

蜂窝夹层板的边长、蜂格尺寸及弹性参数同3.2.1。图6为蜂窝材料杨氏模量在40～200 GPa范围内变化时对不同厚度夹层板固有频率的影响关系曲线。

图6 蜂窝材料弹性参数对蜂窝夹层板固有频率的影响关系曲线Fig.6 Effects of Young’s modulus of core material on natural frequency

由图6和式(19)、式(20)可知，蜂窝材料杨氏模量Es对芯层杨氏模量和夹层板整体弯曲刚度的贡献很小，因此不同厚度夹层板固有频率随Es的增加均没有明显的变化，可见蜂窝材料杨氏模量对夹层板固有频率基本没有影响。

4 结论

针对正交各向异性蜂窝夹层板的弯曲振动问题，应用Reissner-Mindlin夹层板剪切理论，在考虑横向剪切变形的基础上，给出了一种将夹层板弯曲控制方程组化为仅含一个位移函数的单一方程的方法，获得了四边简支矩形夹层板固有频率的精确解，并对面板和芯层各项设计参数对夹层板固有频率的影响进行了分析，结论如下:

(1)用本文方法计算得到的理论结果与数值结果和实验结果的一致性很好，证明了此方法的正确性，这为进一步研究蜂窝夹层板结构的声振特性奠定了基础。

(2)面板厚度增加引起面板弯曲刚度增大，但同时减弱了芯层厚度对夹层板整体弯曲刚度的贡献，夹层板固有频率随面板与夹层板厚度比增大呈略微下降的趋势;面板纵向杨氏模量对夹层板弯曲刚度有正贡献，不同厚度的夹层板固有频率圴呈逐渐上升的变化趋势，上升速度随夹层板厚度的增加而加大。

(3)增大蜂格壁厚和蜂格边长在增强夹层板整体弯曲刚度的同时会降低夹层板的等效密度，夹层板固有频率随d和l的增加呈略微下降的变化趋势;但当夹层板厚度较大、d很小时，d对夹层板弯曲刚度的增强作用较为明显，固有频率随d的增加先上升再下降，而当夹层板厚度较大、l很小时，增大l对夹层板整体弯曲刚度的减弱作用更为显著，固有频率随l增加的下降速度较大。

(4)蜂窝材料杨氏模量Es对夹层板整体弯曲刚度的贡献很小，不同厚度夹层板固有频率随Es的增加均没有明显变化，蜂窝材料杨氏模量不是夹层板固有频率的主要影响因素。

［1］Allen H G.Analysis and design of structural sandwich panels［M］.London:Pergamon Press，1966.

［2］Vinson J R.The behavior of sandwich structures of isotropic and composite materials［M］. Lancaster:Technomic Publishing，1999.

［3］Wang C M. Vibration frequenciesofsimply-supported polygonal sandwich plates via kirchhoff solutions［J］.Journal of Sound and Vibration，1996，190(2):250 －255.

［4］ Monforton G R，Schmit L A J.Finite element analysis of sandwich plates and cylindrical shells with laminate faces［J］.In:Proceedings of the 2nd conference on matrix methods in structural mechanics，Wright-Patterson Air Force Base，Ohio，1969:573－616.

［5］Zhou H B，Li G Y.Free vibration analysis of sandwich plates with laminated faces using spline finite point method［J］.Composite Structure，1996，2:257 －263.

［6］ Raville M E，Veng E S.Determination of natural frequencies of vibration of a sandwich plate［J］.Exp Mech，1967，7:490－493.

［7］中国科学院力学研究所.夹层板壳的弯曲、稳定和振动［M］.北京:中国科学出版社，1977.

［8］石亦平，韩 兰，刘群利，等.蜂窝夹层板自由振动参数影响分析及实验研究［J］.工程力学(增刊)，1999:635－641.

［9］李永强，金志强，王 薇，等.四边简支条件下对称蜂窝夹层板的弯曲振动分析［J］.机械工程学报，2008，44(5):165－169.

［10］Gibson L J，Ashby M F，Schajer G S.The mechanics of twodimension cellular materials［J］.Proc R SocA382，1982;25－42.

［11］富明慧，尹久仁.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31(1):113－118.

［12］ Rao M K，Desai Y M.Analytical solutions for vibrations of laminated and sandwich plates using mixed theory.Composite Structure，2004，63:361 －373.

［13］ Wang T A.Vladimir sokolinsky，shankar rajaram，steven r.Nutt.consistenthigher-orderfree vibration analysis of composite sandwich plates［J］.Composite Structure，2008，82:609－621.