圆弧齿锥齿轮接触动力学分析

姚廷强，王立华，谭 阳

(昆明理工大学 机电工程学院，昆明 650093)

圆弧齿锥齿轮是目前应用最为广泛的相交轴运动传递的基础元件，具有重合度大、传动平稳、承载能力高等优点。随着螺旋锥齿轮朝高速、重载方向的发展，需要更精确的动力学分析，而振动与噪声产生的机理及消除方法则是螺旋锥齿轮动力学理论研究和工程应用等方面亟待解决的关键问题，同时为研制新的性能良好的螺旋锥齿轮和建立尽可能符合实际的螺旋锥齿轮动力学模型提出了更高的要求。

螺旋锥齿轮动态性能研究主要涉及齿面接触分析(TCA)、加载接触分析(LTCA)、考虑齿面摩擦的热分析和润滑分析、非线性动力学的拟动力学方法研究等关键方面［1－2］，后两者是目前螺旋锥齿轮动力学研究的热点问题。方宗德、高建平、杨宏斌和邓效忠［3－7］，黄昌华、郑昌启和李润方［8－9］，林腾蛟［10］，王立华［11］，刘光 磊［12］，唐 进 元［13］，吴 序 堂 和 王 小 椿［14］，杨 先勇［15］，Litvin［16］，Cheng［17］，Tanaka［18］等学者对螺旋锥齿轮动力学的理论研究和工程应用做出了贡献，促进了螺旋锥齿轮技术的发展。随着齿轮啮合基础理论和计算机技术的发展，运用有限元法进行螺旋锥齿轮的齿面接触分析和加载接触分析的设计方法与仿真分析技术日趋成熟。螺旋锥齿轮的有限元法通常研究少量轮齿啮合接触特性，计算效率相对较低，尤其在考虑滚动轴承多体接触动力学特性的螺旋锥齿轮系统动力学分析方面，该方法还存在局限性，有待进一步发展。

在基于多体系统动力学理论的渐开线直齿齿轮接触动力学研究中，李三群［19］，Suzuki等［20］考虑轮齿的Hertz接触变形，运用离散渐开线的弧线－弧线接触算法，建立二维接触动力学模型。Mauer等［21］研究了刚性齿轮啮合传动的二维接触动力学方法。Ebrahimi［22］，姚廷强［23］等研究了刚柔耦合齿轮的二维和三维接触动力学分析方法。众所周知，螺旋锥齿轮啮合传动特性比渐开线直齿齿轮要复杂得多，使得这些渐开线齿轮接触动力学方法不能直接应用于螺旋锥齿轮动力学研究。目前，计及弧齿啮合齿面的动态接触关系的螺旋锥齿轮多体接触动力学方法还处于探索阶段，从文献检索看，还未见相关研究报道。本文运用多体系统动力学方法，研究考虑啮合齿面的动态接触关系的圆弧齿锥齿轮接触动力学特性，为进一步设计与制造出低振动噪声、高可靠性的螺旋锥齿轮提供理论参考。

1 圆弧齿的啮合齿面离散建模方法

1.1 啮合齿面的三角网格模型

UGS公司基于格里森制的弧齿锥齿轮的铣齿加工原理和著名的LITVIN方法［2］，开发了弧齿锥齿轮三维建模模块GearWizard，可有效地计算出啮合齿面的离散三维空间坐标点P。本文运用GearWizard建立了圆弧齿锥齿轮的三维模型，在轮齿轴剖面上沿根锥的齿长方向和齿高方向计算得到圆弧齿啮合齿面的离散点P的三维空间坐标数据，进而建立齿面的三角网格模型，网格的疏密程度根据计算点的数目和精度选取。对逆向工程领域的单有序点列的海量散乱测量数据点，Liang［24］提出一种在两列数据之间构建三角网格近似描述曲面轮廓的方法，从而重构出复杂自由的空间三维曲面。为了降低圆弧齿啮合齿面的动态接触搜索规模，提高计算效率，本文运用三角网格法［24］建立圆弧齿啮合齿面的三角网格模型。由于啮合齿面的三维离散点P在齿宽和齿高方向上均是规则的有序离散点，满足三角网格法的规则有序点要求，无需对数据点进行归类处理，可直接在两路径的离散点之间建立齿面的三角网格单元，进而计算其法向矢量，如图1。

圆弧齿齿面的三角网格法的具体算法步骤为:

Step1:确定基本路径和目标路径。以啮合齿面靠近锥齿轮小端的齿顶边界为起始点wi=1，hi=1，对应的齿宽路径(wi=1，2，…，nw)为基本路径，相邻齿宽路径为目标路径。

图1 圆弧齿齿面的三角网格法Fig.1 The triangle mesh method for spiral bevel gear

Step2:搜索路径间的对应点。计算连接线段数和附加线段数的公式为:

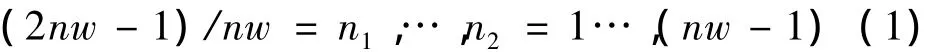
式中商n1=1为基本路径上每点的连接线段，余数n2=nw－1为附加线段总数。

Step3:确定基本路径上需要附加线段的离散点区域。在基本路径上需要附加线段区域的起始点s和结束点e序号为:

啮合齿面相邻两条齿宽路径上的点数量相等时，则整数商n1=1表示在基本路径上的离散点Pwi，hi用1条连接线段连接目标路径上的离散点Pwi，(hi+1)，余数n2=nw－1表示在基本路径上的离散点从第1个点至第nw－1个点的每个点均用1条附加线段连接目标路径上的离散点，共有n2=nw－1条附加线段(如图1)。

Step4:由Step1，2，3和啮合齿面的有序离散点完成线段连接。

Step5:计算每个三角网格单元的单位法向矢量。啮合齿面的三角网格法是为了研究圆弧齿啮合齿面的动态接触关系，因此必须确定三角网格单元的法向矢量(向外)。

如 果 三 角 网 格 单 元 是 由Pwi，hi，Pwi，(hi+1)和P(wi+1)，(hi+1)构成，由离散点构成矢量为:

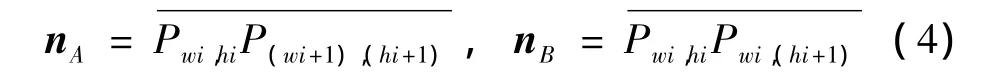
如 果 三 角 网 格 单 元 是 由Pwi，hi，P(wi+1)，hi和P(wi+1)，(hi+1)构成，由离散点构成矢量为:

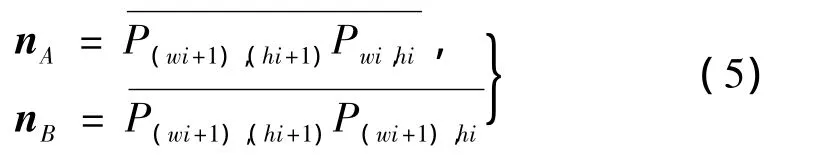
由右手定则和矢量差乘可以计算出每个三角网格单元的外法向矢量为:

忽略圆弧齿锥齿轮的结构弹性变形，考虑啮合齿面的接触弹性变形，在圆弧齿锥齿轮的中心体坐标系下，啮合齿面的三维坐标离散点P的位置和方向是不变的，由此构成啮合齿面的三角网格单元的相对位置和方向也是不变的。因此，只需一次建立啮合齿面的三角网格模型，就可以得到啮合齿面的三角网格单元的位置、方向、顶点和法向矢量等计算数据，为建立考虑啮合齿面动态接触关系的圆弧齿锥齿轮动力学模型奠定了基础。

圆弧齿锥齿轮的参数如表1所示，圆弧齿锥齿轮模型、啮合齿面的空间离散点和三角网格模型如图2所示。

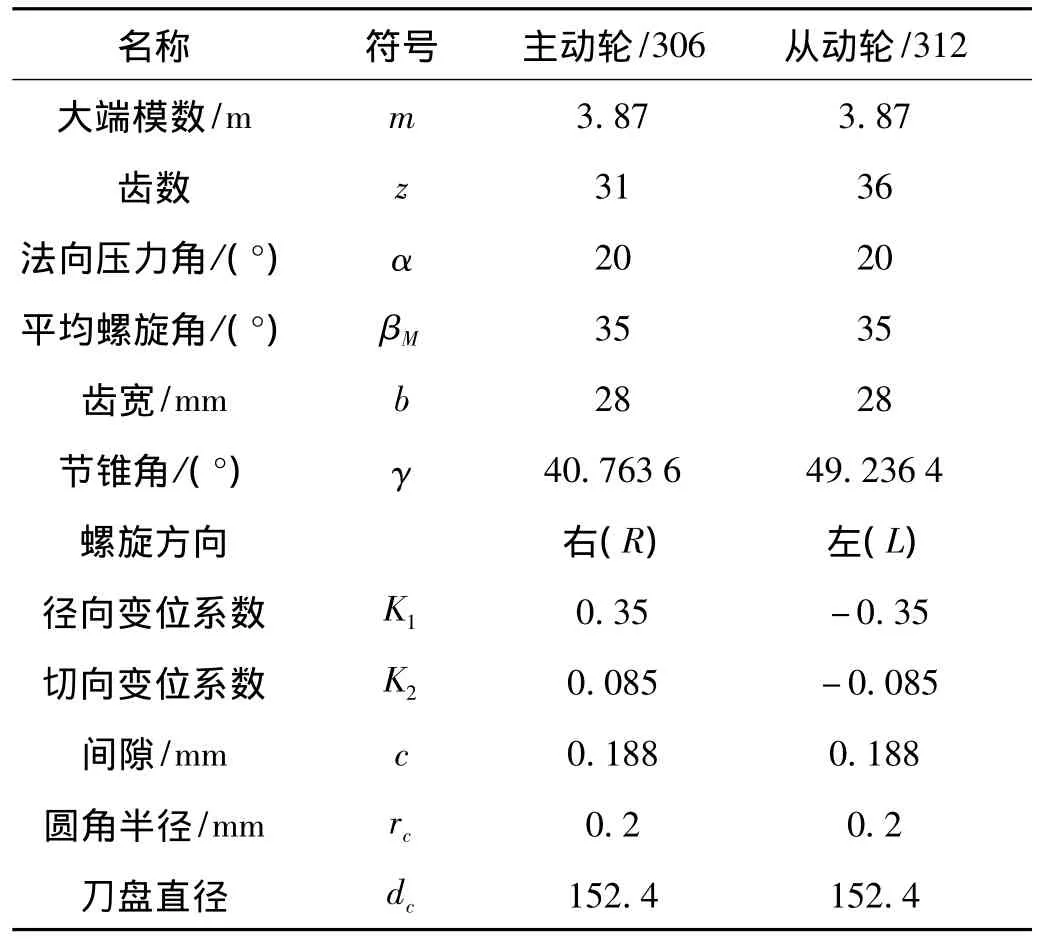
表1 格里森制等距齿型的圆弧齿锥齿轮参数表Tab.1 The parameters of Gleason Spiral Bevel Gear

图2 格里森制的圆弧齿锥齿轮模型Fig.2 The model of spiral bevel gears

1.2 啮合齿面的接触刚度

圆弧齿锥齿轮啮合传动实质上是圆弧齿啮合齿面之间的动态接触的共轭啮合传动，啮合齿面的椭圆接触面和接触刚度满足Hertz点接触条件［2］。用计算圆弧齿的中点M处的平均Hertz接触刚度参数近似描述圆弧齿的单对啮合齿面的接触刚度参数。锥齿轮的材料弹性模量为2.1E11 N/mm2，泊松比为0.3，则圆弧齿的单对啮合齿面的接触载荷和弹性变形之间的非线性关系为［23］:

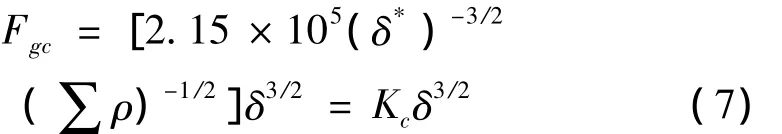
式中Fgc为Hertz接触力，δ为接触弹性变形，Kc为接触刚度参数，δ*是主曲率差F(ρ)的函数，ρ为啮合齿面的主曲率参数［2］。

由式(7)可计算出圆弧齿锥齿轮在啮合齿面中点处的接触刚度参数为Kc=7.2E5 N/mm1.5。

2 圆弧齿锥齿轮啮合接触动力学模型

2.1 啮合齿面动态接触关系

基于啮合齿面的三角网格模型，圆弧齿啮合齿面的动态接触搜索算法的关键在于搜索啮合齿面上的三角网格单元是否发生接触。运用包围盒接触技术［25］确定可能发生接触的少量几个啮合齿面，实现圆弧齿啮合接触的全域搜索区域的缩减，以减小三角网格单元的接触搜索规模。

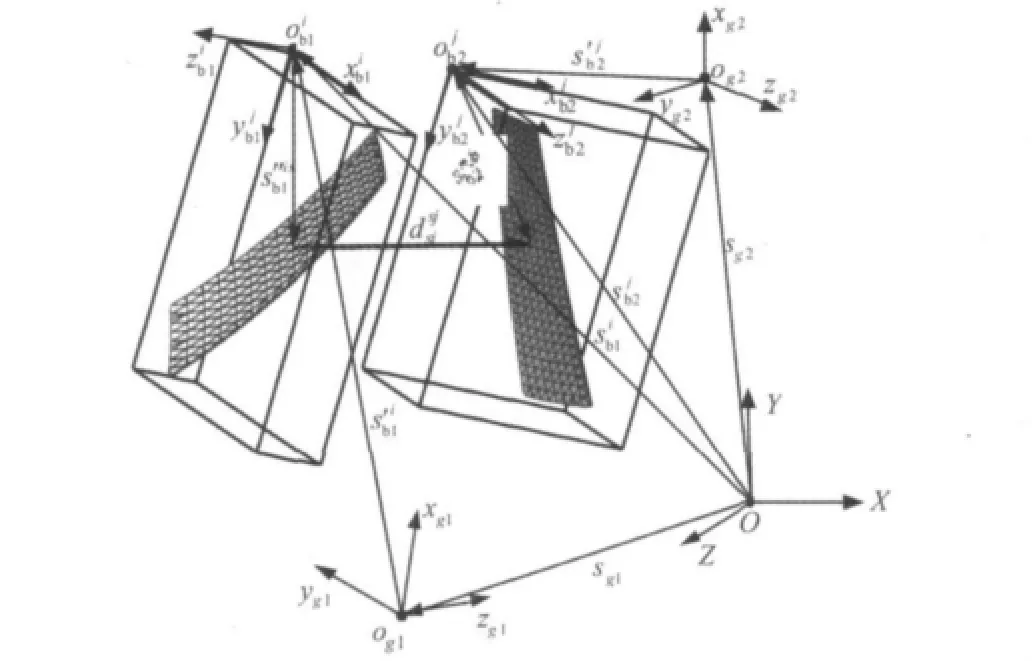
图3 圆弧齿的啮合接触模型Fig.3 The contact model of spiral bevel gears

圆弧齿i和j的啮合齿面的包围合坐标系在绝对坐标系下的位置矢量为:

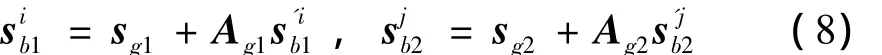
啮合齿面上的三角网格单元之间的相对位移矢量满足如下关系:

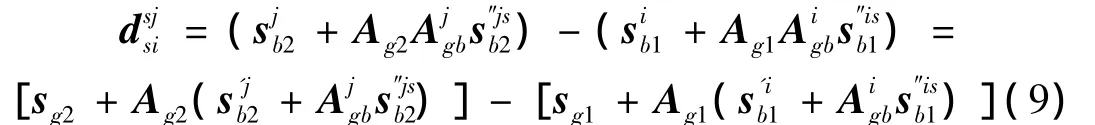
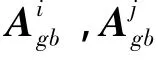
对所有齿面均建立自定向下递推的齿面包围盒树，顶层为第0级包围盒，然后将将第0级的包围盒分解为2个第2级的子包围盒，以此递推，最后使得底层包围盒包含(或相交)少量的三角网格单元。编制啮合齿面的动态接触搜索算法，从第0级顶层包围盒开始接触搜索，如果搜索到包围盒相交状态，则计算程序将递推地继续搜索第2级的子包围盒相交状态;否则，数值算法将跳过第0级包围盒和其下所有子包围盒的后续搜索计算程序。本文忽略圆弧齿锥齿轮的结构弹性变形，在圆弧齿锥齿轮的中心体坐标系下，只需一次建立啮合齿面的包围盒即可实现动态接触搜索过程。

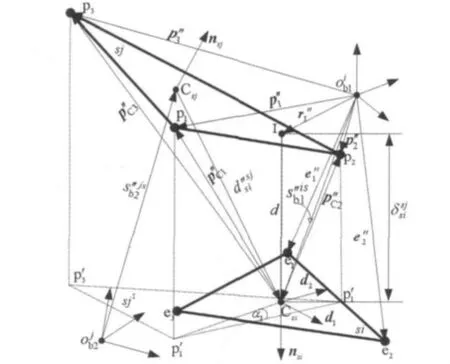
图4 三角网格单元接触关系Fig.4 The contact model of two triangle mesh

当啮合齿面接触搜索到底层包围盒相交时，动态接触搜索算法将计算少量三角网格单元之间的接触状态［25－26］，进而计算动态接触力和力矩(如图4)。

三角网格单元的局部矢量坐标轴(d1，d2)为:

式中e″k是主动锥齿轮轮齿i的啮合齿面的三角网格单元si的顶点ek在包围盒坐标系下的位置矢量，k=1，2，3。为了确定式(10)的直线是否与三角网格单元si相交，则有:

当三角网格单元si的质心位于三角网格单元sj的投影内时，式(10)的法线势必与三角网格单元sj相交。当啮合齿面三角网格单元相交时，则有:

由圆弧齿的齿面离散点可以确定三角网格单元的常数法向量nsi和nsj，将相对位移矢量沿着三角网格单元sj的法向nsj投影可得相对渗透量(如图4所示)。

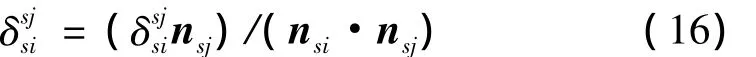
当啮合齿面的三角网格单元之间发生接触时，圆弧齿的啮合齿面的动态接触力的一般形式为:

式中Fgc为动态接触力，δ为相对渗透量，step(…)为半正矢阶梯函数，Kc为Hertz接触刚度，δ为轮齿上接触对间的法向渗透深度，δmax为接触对间的接触阻尼比cmax时的最大渗透深度。将式(17)中动态接触力Fgn在锥齿轮的体坐标系中投影转换为坐标轴分量，可计算出力矩Mt。

2.2 圆弧齿锥齿轮动力学方程

如图2定义初始理论位置时两齿轮轴线的交点为绝对坐标系的原点O，主动轮1(小轮)的体坐标系og1xg1yg1zg1方向与绝对坐标系OXYZ相同，从动齿轮2(大轮)的体坐标系og2xg2yg2zg2的xg2、yg2、zg2方向分别与绝对坐标系OXYZ的Z，X，Y方向相同。圆弧齿锥齿轮的运动坐标定义为:

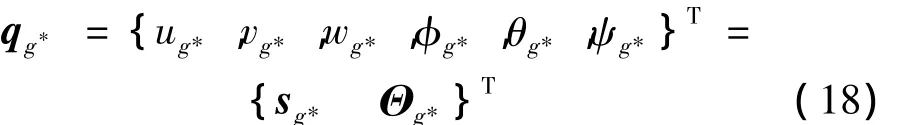
式中*表示主从动齿轮1和2，ug*，vg*，wg*分别为主、从动齿轮的平动自由度，φg*，θg*，ψg*分别为主、从动齿轮的转动自由度，即锥齿轮的体坐标系在绝对坐标系下的方向角。

刚性支承下圆弧齿锥齿轮仅有绕其体坐标系的zg*轴的旋转自由度ψg*，具体的约束方程为ug1=0，vg1=0，wg1=0，φg1=0，θg1=0，ψg1－ ωg1t=0，ug2=0，vg2=0，wg2=0，φg2=0，ψg2=0。因此锥齿轮动力学方程为:

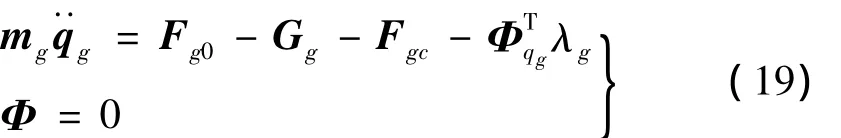
式中mg为圆弧齿锥齿轮的质量和惯量矩阵，Fg0和Fgc分别外力和啮合接触力列向量，Gg为重力列向量，，λg分别为雅可比矩阵和拉格朗日乘子列向量。Φ=［Φg1Φg2］T为约束方程列向量。

本文基于ADAMS多体动力学仿真软件，运用HHT数值计算方法求解式(19)，编制自定义用户程序和圆弧齿锥齿轮全齿面动态接触搜索程序，计算圆弧齿锥齿轮三维全齿面动态接触力学特性。

3 圆弧齿锥齿轮啮合传动接触动力学分析

3.1 圆弧齿啮合全齿面接触动力学特性

本文主要基于考虑圆弧齿的啮合全齿面动态接触关系的弧齿锥齿轮三维空间动力学模型，研究仅有转动自由度下圆弧齿锥齿轮啮合传动的全齿面接触动力学特性和响应特性。主动锥齿轮的驱动转速为ng1==1 800 r/min，齿面的接触刚度和阻尼参数为Kc=7.2E5 N/mm1.5，cmax=50 N·s/mm。

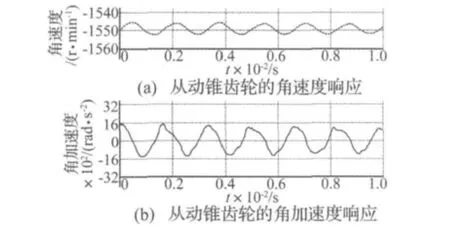
图5 从动锥齿轮的角速度和角加速度响应结果Fig.5 The angular velocity and angular acceleration of driven gear

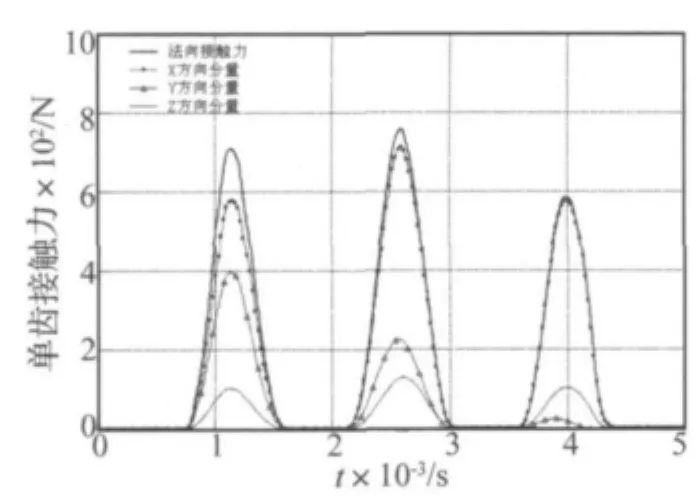
图6 单对齿的齿面接触力Fig.6 The contact force of one pair teeth’s surfaces

图5为锥齿轮空转时从动锥齿轮的角速度和角加速度响应结果。随着主动锥齿轮运动的传递，圆弧齿的啮合齿面将产生法向Hertz接触力和接触弹性变形，在实际传动过程中，主动锥齿轮的运动实质上是由圆弧齿啮合齿面的接触动力学关系传递给从动锥齿轮。从动锥齿轮在理论传动角速度1 550 r/min附近呈周期变化，波动幅值相对误差为－2% ～1.68%满足传动设计要求，也说明提出的动力学模型能较好地模拟实际弧齿锥齿轮的传动特性。

图6和图7分别为锥齿轮空转时单对圆弧齿的啮合齿面的接触力和力矩。当圆弧齿的啮合齿面发生接触时，随着齿面的接触弹性变形的增加，齿面法向接触力增加，从而形成驱动力矩，迫使从动锥齿轮的角速度逐渐增加。在啮合齿面接触弹性变形的恢复(回弹)过程中，齿面法向接触力逐渐减小，从动齿轮的角速度也会相应减小，因此齿面法向接触力呈抛物线规律的周期平滑变化。

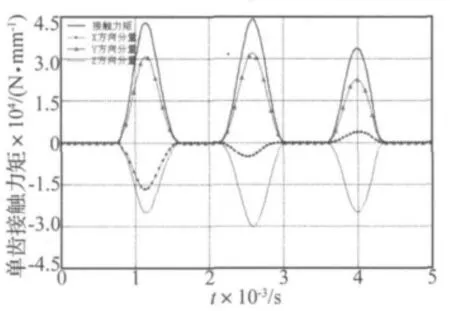
图7 单对齿的力矩Fig.7 The contact moment of one pair teeth’s surfaces

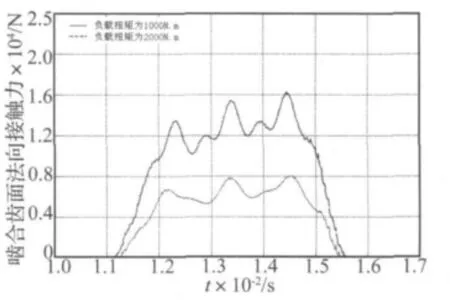
图8 单对齿的齿面法向接触力Fig.8 The contact force of one pair teeth’s surfaces

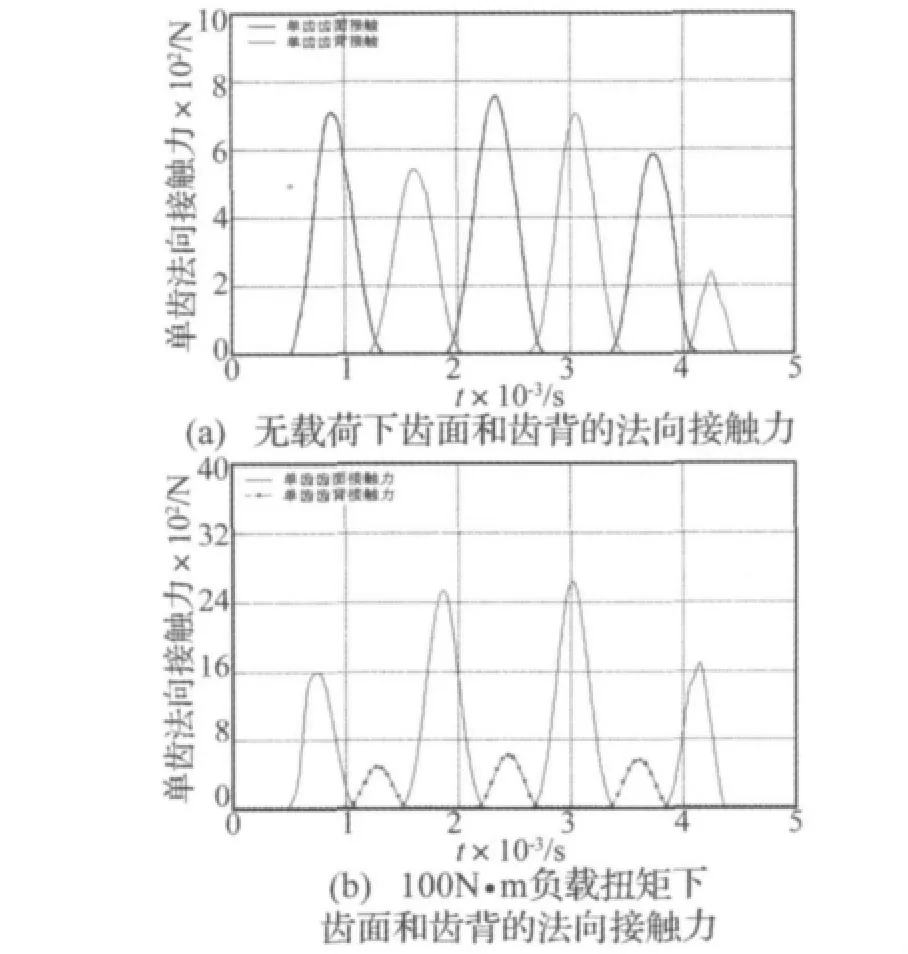
图9 从动锥齿轮的齿面齿背的法向接触力Fig.9 The contact force of double surface contact of mesh teeth

齿面接触弹性变形回弹过程中，空转时没有负载扭矩足以抑制齿面接触弹性变形回弹时形成的反力矩，这将使啮合齿面发生脱离啮合的现象，从而引起啮合圆弧齿的齿背发生接触的现象(图9)。

图8为从动锥齿轮受不同负载扭矩时单对圆弧齿啮合齿面的法向接触力。随着从动锥齿轮负载扭矩的增加，啮合齿面的法向接触力增加，齿背的接触力减小图9(b)。分析图8可知，当从动锥齿轮负载扭矩足以抑制啮合齿面的接触弹性变形的回弹引起的反力矩时，在轮齿接触弹性变形的回弹过程中，啮合齿面将始终保持啮合接触，从而产生啮合齿面的接触弹性变形和接触力，圆弧齿的齿背将不会发生啮合接触。随着负载扭矩的增加，啮合齿面的法向接触力也相应的增加。

3.2 啮合圆弧齿双侧接触分析

图9分别为无负载扭矩和负载扭矩为100 N·m下单对齿的啮合齿面的法向接触力。空转时在啮合传动过程中进入啮合区域的单对齿将发生三次齿面和三次齿背的啮合接触。从动齿轮受100 N·m负载扭矩时在啮合传动过程中进入啮合区域的单对圆弧齿发生四次齿面和三次齿背的啮合接触，而且每次发生接触时齿面的法向接触力大于齿背的。比较分析图9(a)、(b)知，从动锥齿轮受负载扭矩时单对圆弧齿齿面的啮合接触时间比空转时明显增加，而齿背的啮合接触时间则是明显减少。

计算结果说明单对圆弧齿是平滑进入齿面啮合及退出啮合的，圆弧齿锥齿轮具有良好的传动平稳性，而且为弧齿锥齿轮动态设计提供了轮齿接触强度校核与疲劳寿命预测的有效全齿面啮合接触的参考数据。

3.3 啮合弧齿传动动力学特性

图10为负载扭矩为1 000 N·m时在不同齿侧侧隙下相邻8颗圆弧齿啮合传动的法向接触力。圆弧齿锥齿轮在啮合传动过程中同时有4对圆弧齿发生啮合齿面的动态接触，由此得到啮合重合系数为4，与理论重合系数一致［2］，证实了考虑圆弧齿啮合齿面动态接触关系的弧齿锥齿轮接触动力学模型是有效的。计算结果真实地表明了圆弧齿锥齿轮啮合接触的传动特点，揭示了圆弧齿锥齿轮的传动承载特性。

计算结果表明当第1颗轮齿完全退出啮合接触时，第5颗轮齿开始进入啮合接触区域发生啮合齿面接触，此时负载扭矩主要由啮合接触区内的其余三颗轮齿承载(第2、3和4颗轮齿)，则这三颗轮齿的啮合齿面法向接触力达到极大值。此时其余三颗轮齿处于不同的啮合位置，其法向接触力的极大值也是不同的，而且按照先后进入啮合区域的顺序逐渐减小。随着主动锥齿轮的转动，当第5颗轮齿逐渐进入啮合接触区域时其啮合齿面法向接触力逐渐增加，在此过程中第2颗轮齿也逐渐退出啮合接触区域，当第2和5颗轮齿的啮合齿面的法向接触力相等时，第3和4颗轮齿的啮合齿面法向接触力达到极小值。当第2颗轮齿完全退出啮合接触区域时，其余三颗轮齿(第3、4和5颗轮齿)的啮合齿面法向接触力又达到极大值，圆弧齿啮合传动将如此反复。

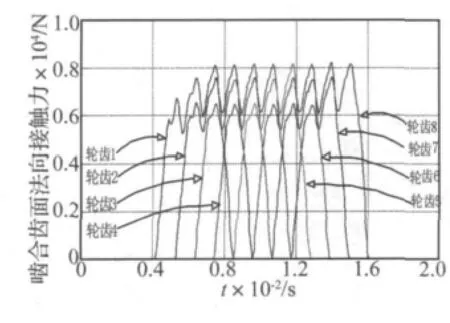
图10 侧隙为0.05 mm下啮合齿面的法向接触力Fig.10 The contact force of multi-tooth meshing

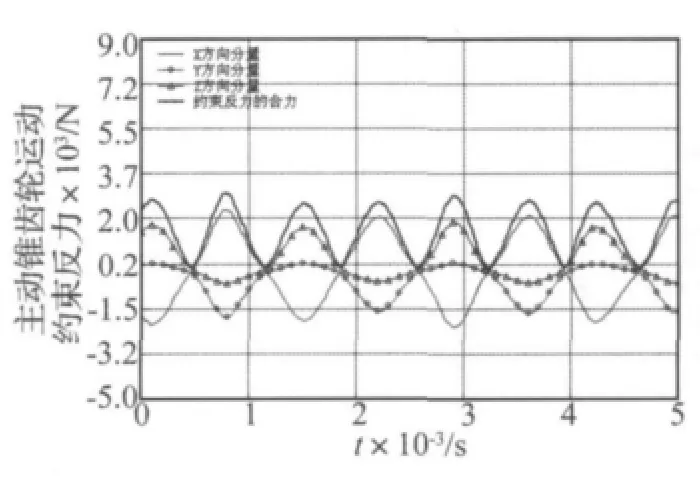
图11 主动锥齿轮的运动约束反力Fig.11 The constraint force of driving gear

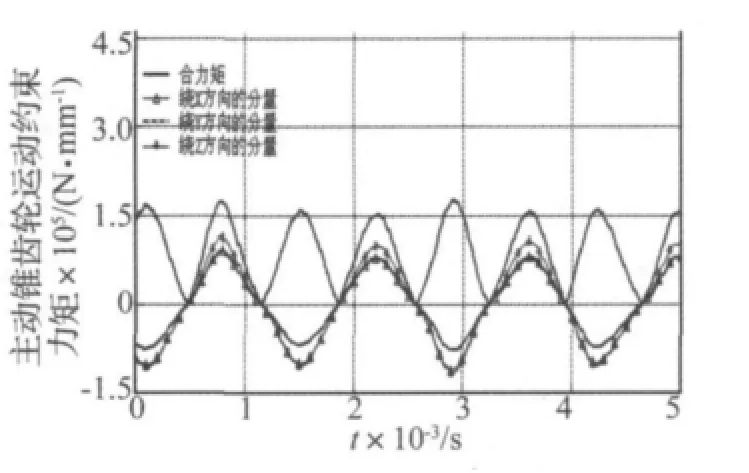
图12 主动锥齿轮的运动约束反力矩Fig.12 The constraint moment of driving gear

计算结果进一步表明了在圆弧齿锥齿轮啮合传动过程中，当有圆弧齿退出啮合接触时，受齿侧侧隙和负载扭矩等的影响，同时有圆弧齿进入啮合接触，此时啮合齿面的法向接触力将达到极大值，随着主动锥齿轮的传动，之后也将出现极小值。由于计算实例中圆弧齿锥齿轮啮合传动的重合系数为4，因此，每颗轮齿经过整个啮合接触区域时，将会出现3次圆弧齿的啮入啮出交替变化，从而使每颗圆弧齿啮合齿面的法向接触力也出现3次极大值和极小值的交替变化规律。而且每颗圆弧齿在整个啮合接触区内历经了从进入啮合接触逐渐退出啮合接触的位置变化，同时啮合齿面接触位置是从锥齿轮的小端向大端逐渐移动，从而使每颗轮齿进入啮合接触区域后啮合齿面法向接触力的极值逐渐增大。

图11和图12分别为锥齿轮空转时主动锥齿轮的运动约束反力和反力矩。分析可知，由于圆弧齿锥齿轮在传动啮合过程中齿面产生法向动态啮合力，从而得到沿径向、切向和轴向的动态啮合力分量。主动锥齿轮的约束反力和反力矩均是周期平滑变化的，计算结果表明了圆弧齿锥齿轮的啮合传动特性具有较好的传动平稳性。

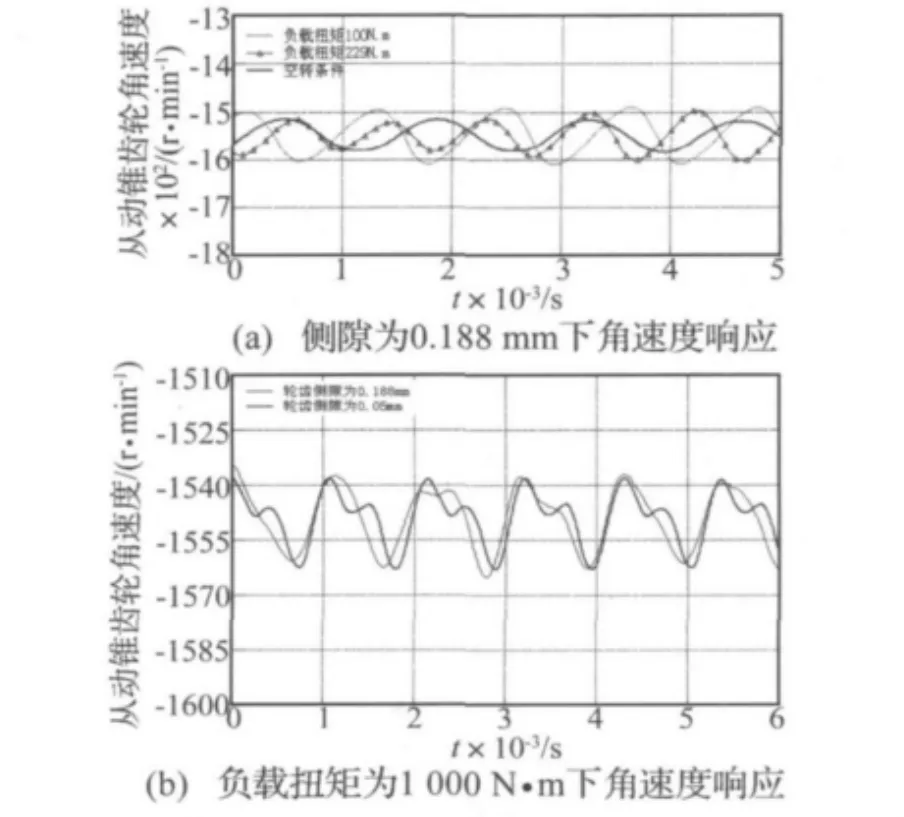
图13 从动锥齿轮角速度与负载扭矩、侧隙的关系Fig.13 The relationship between angular velocity，torque and backlash

图13为不同负载扭矩和侧隙对从动锥齿轮角速度的影响。对比分析图13(a)和(b)的不同负载扭矩下的计算结果可知，在空转和较小负载扭矩条件下，从动锥齿轮的角速度周期变化规律是相似的，此时角速度的波幅相对较大。在较大负载扭矩下圆弧齿并未发生齿背接触，此时角速度波幅相对较小。圆弧齿锥齿轮的侧隙对角速度幅值的影响较小，但对其变化规律有一定的影响。作者还发现在平稳的速度和负载扭矩下侧隙对单齿啮合接触时间、啮合齿面法向接触力的幅值和变化规律的影响较小，这为在工作状态下冲击速度和冲击负载不明显的机械系统动力学设计提供了参考。

4 结论

在螺旋锥齿轮系统动力学研究中，运用考虑圆弧齿的啮合全齿面三维动态接触关系的螺旋锥齿轮接触动力学模型，可以从系统层次上研究螺旋锥齿轮传动系统的动力学响应特性。这对螺旋锥齿轮传动系统的动力学设计与改进、动力学分析提供了理论指导和参考数据。

(1)建立了考虑圆弧齿的啮合全齿面三维动态接触关系，转速和负载等因素的螺旋锥齿轮三维空间动力学模型，计算出圆弧齿的啮合全齿面动态接触力学特性和动态响应特性，直接反应出螺旋锥齿轮啮合传动的接触动力学行为，为弧齿锥齿轮动态设计提供了轮齿接触强度校核和疲劳寿命预测的有效啮合全齿面接触载荷的参考数据。

(2)由于圆弧齿锥齿轮的啮合重合系数比较大，而且每颗轮齿是逐渐进入或退出啮合接触区域的，在忽略支承条件影响下，圆弧齿锥齿轮的啮合传动过程是十分平稳的，圆弧齿的啮入啮出并不会引起明显的冲击振动响应。计算结果证实了圆弧齿锥齿轮啮合传动的这一本质特性，较好地模拟了螺旋锥齿轮的啮合传动特性。

(3)考虑圆弧齿的啮合全齿面三维动态接触关系，更真实地模拟了螺旋锥齿轮啮合传动特性，具有较高的计算效率和稳定性。建立的圆弧齿锥齿轮接触动力学模型为考虑冲击速度、冲击载荷、等效弹性支承方法或滚动轴承多体接触动力学特性等因素的螺旋锥齿轮系统动力学研究提供了理论基础。

［1］汪中厚，周晓玲.螺旋锥齿轮动力学研究方法及进展［J］.中国机械工程，2006，17(11):1203 －1206.

［2］Litvin F L.Gear geometry and applied theory［M］.New Jersey:Prentice Hall，second virsion，2004.

［3］高建平，方宗德，杨宏斌.螺旋锥齿轮边缘接触分析［J］.航空动力学报，1998，13(3):289 －292.

［4］方宗德，邓效忠，任东锋，等.考虑边缘接触的弧齿锥齿轮承载接触分析［J］.机械工程学报，2002，38(9):69 －72.

［5］邓效忠，方宗德，张金良，等.弧齿锥齿轮高重合度设计［J］.中国机械工程，2002，13(9):791 －795.

［6］杨宏斌，高建平，邓效忠，等.弧齿锥齿轮和准双曲面齿轮非线性动力学研究［J］.航空动力学报，2004，19(1):54－57.

［7］周彦伟，杨宏斌，邓效忠.高齿准双曲面齿轮的轮齿加载接触分析［J］.中国机械工程，2002，13(14):1181－1183.

［8］李润方，黄昌华，郑昌启，等.弧齿锥齿轮和准双曲面齿轮轮齿接触有限元分析［J］.机械工程学报英文版，1995，8(1):82－86.

［9］郑昌启，黄昌华，吕传贵.螺旋锥齿轮加载接触分析计算原理［J］.机械工程学报，1993，29(4):50 －54.

［10］林腾蛟，李润方，郭晓东，等.准双曲面齿轮三维间隙非线性冲击特性分析［J］.中国机械工程，2003，7(14):727－731.

［11］王立华，李润方，林腾蛟，等.弧齿锥齿轮传动系统的耦合振动分析［J］.中国机械工程，2006，14:1431－1434.

［12］刘光磊.弧齿锥齿轮传动动态接触特性研究［D］.西安:西北工业大学，2000.

［13］唐进元，卢延峰，周 超，等.有误差的螺旋锥齿轮传动接触分析［J］.机械工程学报，2008，44(7):16 －23.

［14］吴序堂，王小椿，李 峰.曲线齿锥齿轮三阶接触分析法的原理及传动质量评价［J］.机械工程学报，1994，30(3):47－57.

［15］杨先勇，周晓军，林 勇，等.螺旋锥齿轮间隙非线性系统的分岔与混沌［J］.振动与冲击，2008，27(11):115 －120.

［16］ Litvin F L，Ftentes A，Hayasaka K.Design，Mamufacture，stress analysis，and experimental tests of low noise high endurance spiral bevel gears［J］.Mechanism and Maehinetheory，2006，41(1):83 －118.

［17］ Cheng Y， Lim T C. Vibration analysis ofhypoid transmissions applying an exact geometry-based gear mesh theory［J］.Journal of Sound and Vibration，2001，240(3):519－543.

［18］Tanaka N，Ohno K，Innami T.Dynamic load on spiral bevel gears［J］.The JSME International Conference on motion and Power Transmission，Fukuoka，Japan，2001:27 －32.

［19］李三群，贾长治，武彩钢，等.基于虚拟样机技术的齿轮啮合动力学仿真研究［J］.系统仿真学报，2007，4:901 －904.

［20］ Suzuki D，Horiuchi S，Choi J H.Dynamic analysis of contacting spur gear pair for fast system simulation［J］.Trans Tech Publications，2006，110:151 －162.

［21］ Mauer L.Force element 225 gear wheel［R］.Internal Report，Intec GmbH，Wessling，Germany，2005.

［22］ Ebrahimi S，Eberhard P.Rigid-elastic modeling of gear wheelsin multibody systems［J］. Multibody System Dynamics，2006，16:55 －71.

［23］姚廷强，迟毅林，黄亚宇，等.刚柔耦合齿轮三维接触动力学建模与振动分析［J］.振动与冲击，2009，28(2):167－172.

［24］Liang S R，Lin A C.Probe-radius compensation for 3D data points in reverse engineering［J］.Computers in Industry，2002，48:241 －251.

［25］ Hippmann G.An algorithm for compliant contact between complexly shaped bodiesin multibody dynamics［J］.Multibody System Dynamics，2004，12:345 －362.

［26］ Moller T.A fast triangle-triangle intersection test［J］.Journal of graphics tools，1997，2(2):25 －30.