椭圆钴纳米环磁化动力学研究

叶晴莹，李铭领，吴洋洋，杨 莉，朱伟波，陈水源，黄志高

(福建师范大学物理与能源学院，福建福州350108)

椭圆钴纳米环磁化动力学研究

叶晴莹，李铭领，吴洋洋，杨 莉，朱伟波，陈水源，黄志高

(福建师范大学物理与能源学院，福建福州350108)

利用Monte－Carlo方法模拟了不同偏心率、不同厚度的椭圆钴纳米环的磁特性.模拟结果表明:当系统的偏心率较小时，厚度越大的椭圆钴纳米环的涡旋态(“vortex”态)越稳定，此系统的磁滞回线保持圆形纳米环的主要特征;系统的偏心率较大时，系统的磁特性与圆形纳米环有较大差别，涡旋态的稳定性与厚度并无明显关联;对椭圆钴纳米环的自旋组态分析发现，椭圆系统在极化态(“onion”态)与涡旋态之间出现了更多的亚稳态.

椭圆钴纳米环;偏心率;厚度;磁滞回线;自旋组态

0 引言

由于磁性纳米材料可用于高密度存储，因此近年来磁性纳米材料研究一直倍受关注［1－3］.已有资料表明，方形、矩形或其他多边形纳米磁性材料不适用于高密度存储［4－5］，而圆形纳米材料可较有效地阻止边缘磁畴形成，并减少杂散场，从而形成稳定的涡旋态［1，6－7］.因此，圆形纳米材料可用于制作高密度存储器.然而圆盘形纳米材料的涡旋态中心存在高能涡旋，使重复磁化反转困难［8］，因此圆盘系统并非存储器的最优材料.为了解决这个问题，人们设计出环形纳米磁性材料 (简称纳米环).纳米环不仅具有圆形磁性材料的优点，且当处于涡旋态时中心不存在高能涡旋［9－11］，这使多次磁化反转易于实现，所以纳米环磁性材料在高密度存储方面具有巨大潜力［12－13］.本课题组已对纳米环进行了一些研究，并取得了一些有意义的结果［14－16］.在研究过程中发现，纳米磁性材料的几何形状对自旋组态起着重要作用［4，14－16］，而批量制作纳米环时，精确度常难以达到100%，因此不可避免地会产生部分椭圆形纳米环，这将使系统的磁特性发生变化.本文主要研究椭圆纳米环对系统磁特性的影响，以期为实验提供理论指导.

1 模型和方法

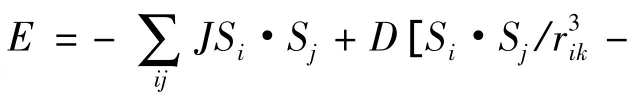
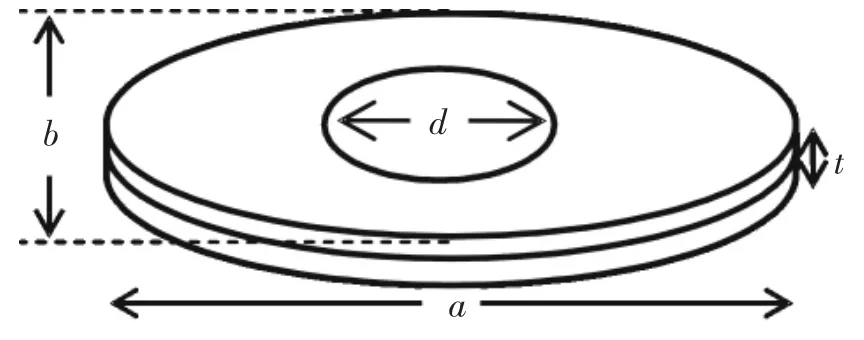
图1 椭圆钴纳米环模型Fig.1 The model of ellipse Co nanoring.

2 结果与讨论

图2分别给出了长轴a=200 nm，短轴b=160 nm，内径d=40 nm，厚度t为10 nm、20 nm、30 nm、40 nm的椭圆钴纳米环的磁滞回线.定义一个处于涡旋态的台阶宽度△Hfc［18］，如图2(a)所示.从图2中可以明显看到，台阶宽度△Hfc随着厚度的增大而增大.利用文献 ［16］的理论:△Hfc越大，涡旋态所对应的磁场强度H的范围就越大，即外加磁场可以在更大的范围内变化，但系统依然可保持涡旋态 (涡旋态稳定).因此△Hfc可以用来表征涡旋态的稳定性［16］.由此可见，对于偏心率较小的椭圆钴纳米环，其结果与圆形纳米环的结果有相似之处［16］，即厚度越大的椭圆钴纳米环的涡旋态越稳定，此结论与实验事实相符［18］.另外，从图2b、图2c、图2d中可以发现，对于较大厚度 (t=20 nm，30 nm，40 nm)椭圆钴纳米环，其磁滞回线呈现多个台阶，这意味着从涡旋态转变到极化态之间存在多个亚稳态，此结论亦与圆形纳米环类似［16］.综上所述，当系统的偏心率较小时，系统的磁滞回线依然保持圆形纳米环的主要特征.

但上述结论对于偏心率较大的椭圆钴纳米环不再适用.图3分别给出了长轴a=200 nm，短轴b=100 nm，内径d=40 nm，厚度t为10 nm、20 nm、30 nm、40 nm的椭圆钴纳米环的磁滞回线.从图3中并没有观察到台阶宽度△Hfc随着厚度的增大而增大.相反，在图3b、图3c中的台阶宽度显得尤为狭小，即涡旋态不再稳定.同时，图3b、图3c在涡旋态与极化态之间呈现多台阶化，即系统出现多个亚稳态，但在图3d中多台阶化却已不再清晰.这说明当系统的偏心率较大时，系统的磁特性与圆形纳米环有较大差别.

出现这种现象的原因在于:对于短轴较长、偏心率较小的系统，其几何形状与圆形系统较接近，因此其磁特性与圆形纳米环相似;而对于短轴较小、偏心率较大的系统，其几何形状与圆形系统相距甚远，所以磁滞回线与圆形钴纳米环有较大差别.上述结果说明椭圆钴纳米环涡旋态的稳定性与纳米环的偏心率、厚度密切相关，即涡旋态的稳定性具有明显的尺寸效应.这一模拟结果对于实验设计以及钴纳米环的实际应用具有很好的参考意义.

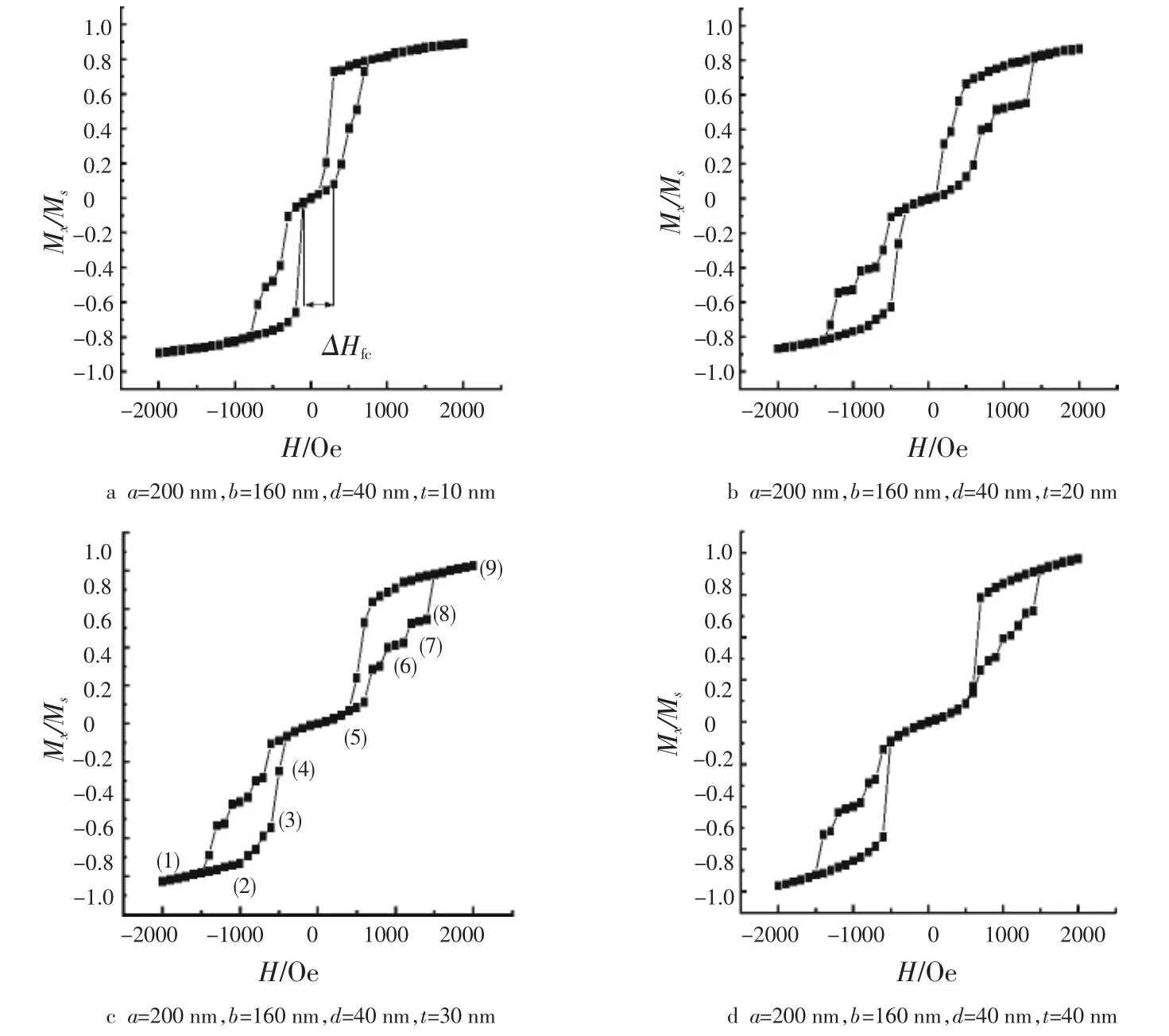
图2 a=200 nm、b=160 nm、d=40 nm及不同厚度椭圆钴纳米环磁滞回线Fig.2 The hysteresis loops of ellipse Co nanorings with different thickness for a=200 nm,b=160 nm,d=40 nm

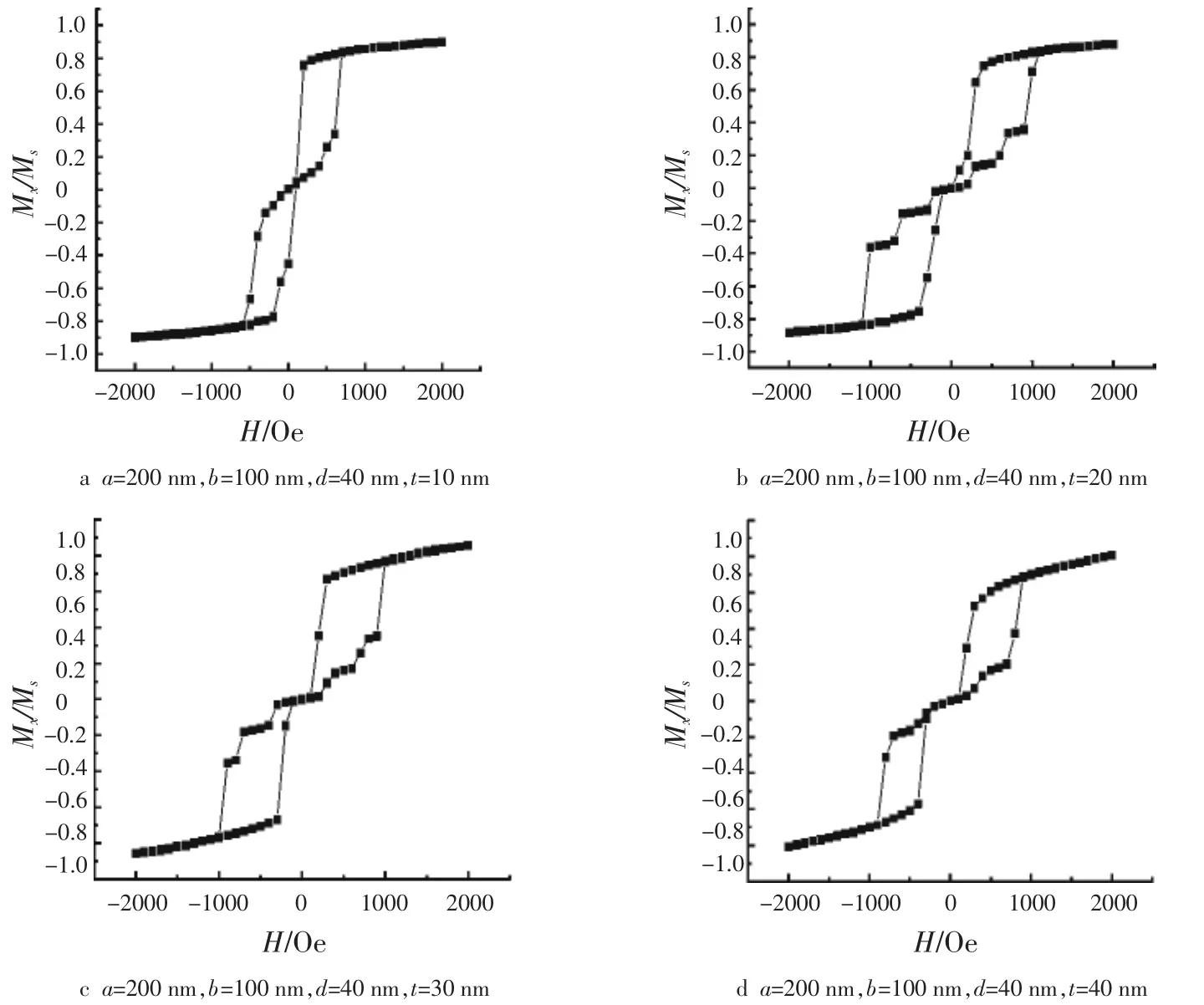
图3 a=200 nm、b=100 nm、d=40 nm及不同厚度椭圆钴纳米环磁滞回线Fig.3 The hysteresis loops of ellipse Co nanorings with different thickness for a=200 nm,b=100 nm,d=40 nm

为了进一步理解椭圆钴纳米环的磁化过程，以a=200 nm、b=160 nm、d=40 nm，t=30 nm的椭圆钴纳米环为例，详细展示系统在磁化过程中的自旋翻转及畴壁运动过程.由于系统各层次的自旋组态基本类似，图4给出该系统中一层的自旋组态用以研究.首先，当外加磁场很大时 (图2c中的(1)点)，系统对应的自旋组态为极化态 (如图4(1));然后，由于外场的减小，系统的自旋发生翻转，在右下方边缘形成一逆时针局域涡旋 (如图4(2))，此时系统的磁化强度减小 (图2c中的(2)点);接着，外加磁场继续减小 (如图2c中的 (3)点)，自旋在外场的作用下于系统的左上方又形成一顺时针局域涡旋 (如图4(3))，此时系统同时存在2个局域涡旋;随着外场的持续减小，当H=－500 Oe时 (图2c中的 (4)点)，2个局域涡旋的畴壁在运动中湮灭，但在系统的右上方再次形成一顺时针局域涡旋 (如图4(4))，此时系统已接近涡旋态;当磁场减小为0时 (图2c中的(5)点)，系统畴壁在运动中全部湮灭，呈现出一个完整的涡旋态 (如图4(5))，系统磁化强度接近于0;接着外磁场反向增大，当H=700 Oe时 (图2c中的 (6)点)，系统呈现2个顺时针局域涡旋 (如图4(6));外磁场从700 Oe～1300 Oe的过程中 (图2c中的 (6)— (8))，系统的畴壁逐渐下移 (如图4(6)— (8));最后，畴壁湮灭在下方边缘，系统再次呈现自旋极化态 (如图4(9)).

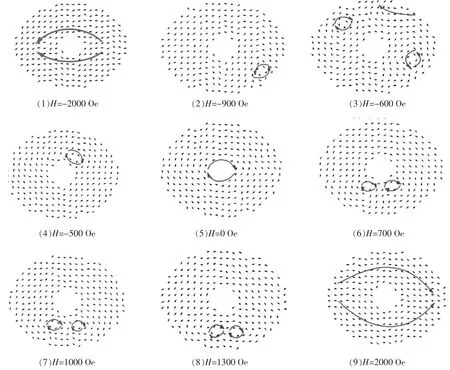
图4 a=200 nm、b=160 nm、d=40nm、t=30nm椭圆钴纳米环自旋组态Fig.4 The spin configurations of Co nanorings for a=200 nm,b=160 nm,d=40 nm,t=30 nm

从系统的磁化过程可以看出，椭圆钴纳米环保留了圆形纳米环的主要特征，即系统外场较大时呈现极化态，磁场为零时呈现完整的涡旋态［16］.但由于尺寸效应，椭圆钴纳米环的磁化过程比圆形纳米环的更为复杂［16］，出现了更多的过渡状态 (亚稳态).

3 结论

利用Monte－Carlo方法模拟了不同偏心率、不同厚度的椭圆钴纳米环的磁特性，模拟结果表明:当系统的偏心率较小时，厚度越大的椭圆钴纳米环的涡旋态越稳定，此结论与实验事实相符，同时，由于尺寸接近圆形纳米环，系统的磁滞回线依然保持圆形纳米环的主要特征;系统的偏心率较大时，由于尺寸与圆形纳米环相距甚远，系统的磁特性与圆形纳米环有较大差别;椭圆钴纳米环涡旋态的稳定性具有明显的尺寸效应;对椭圆钴纳米环的自旋组态分析发现，系统的磁化过程存在极化态与涡旋态，但相对圆形纳米环而言，系统在极化态与涡旋态之间出现了更多的亚稳态.

［1］ WACHOWIAK A，WIEBE J，BODE M，et al.Direct observation of internal spin structure of magnetic vortex cores［J］.Science，2002，298(5593):577－580.

［2］ ZHANG W，HASS STEPHAN.Phase diagram of magnetization reversal processes in nanorings［J］.Phys Rev B，2010，81(6):064433－064438.

［3］ KIWI M.Exchange bias theory ［J］.J Magn Magn Mater，2001，234:584－595.

［4］ COWBURN R P.Property variation with shape in magnetic nanoelements ［J］.J Phys D，2000，33(1):1－16.

［5］ DUNIN－BORKOWSKI R E，MCCARTNEY M R，KARDYNAL B，et al.Off－axis electron holography of patterned magnetic nanostructures ［J］.J Microsc，2000，200(3):187－205.

［6］ SHINJO T，OKUNO T，HASSDORF R，et al.Magnetic vortex core observation in circular dots of permalloy ［J］.Science，2000，289(5481):930－932.

［7］ CHOE S B，ACREMANN Y，SCHOLL A，et al.Vortex core－driven magnetization dynamics ［J］.Science，2004，304(5669):420－422.

［8］ VAZ C A F，LOPEZ－DIAZ L，KLÖUI M，et al.Direct observation of remanent magnetic states in epitaxial fcc Co small disks ［J］.Phys Rev B，2003，67(14):140405－140408.

［9］ ZHU X B，GRÜTTER P，METLUSHKO V，et al.Construction of hysteresis loops of single domain elements and coupled permalloy ring arrays by magnetic force microscopy ［J］.J Appl Phys，2003，93(10):8540－8542.

［10］ ZHOU W L，HE J B，FANG J Y，et al.Self－assesmbly of FePt nanoparticles into nanorings ［J］.J Appl Phys，2003，93(10):7340－7342.

［11］ KONG X Y，DING Y R，YANG R S，et al.Single－crystal nanorings formed by epitaxial self－coiling of polar nanobelts［J］.Science，2004，303(5662):1348－1351.

［12］ AKERMAN J.Toward a universal memory ［J］.Science，2005，308(5721):508－510.

［13］ ZHU J G，ZHENG Y，PRINZ G A.Ultrahigh density vertical magnetoresistive random access memory［J］.J Appl Phys，2000，87(9):6668－6673.

［14］林枝钦，叶晴莹，钟克华，等.不对称钴纳米环磁特性及涡旋态控制的蒙特卡罗模拟 ［J］.计算物理，2010，27(1):143－149.

［15］ YE Q Y，CHEN S Y，ZHONG K H，et al.Magnetic properties for cobalt nanorings:Monte Carlo simulation ［J］.Physica B，2012，407(4):790－794.

［16］ LIN Z Q，ZHONG K H，YE Q Y，et al.The size effects of the magnetic properties for the 200 nm Co nanorings:Monte－Carlo simulation ［C］ //Second IEEE International Nanoelectronic Conference Proceedings.Shanghai:INEC，2008:677－680.

［17］ HUANG Z G，CHEN Z G，PENG K，et al.Monte－Carlo simulation of tunneling magnetorisistance in nanostructured materials ［J］.Phys Rev B，2004，69(9):094420－094426.

［18］ LI S P，PEYRADE D，NATALI M.Flux closure structures in cobalt rings ［J］.Phys Rev Lett，2001，86(6):1102－1105.

(责任编辑 马建华 英文审校 黄振坤)

Magnetic Dynamic Properties for Ellipse Co Nanorings

YE Qing－ying，LI Ming－ling，WU Yang－yang，YANG Li，ZHU Wei－bo，CHEN Shui－yuan，HUANG Zhi－gao
(College of Physics and Energy，Fujian Normal University，Fuzhou 350108，China)

Based on the Monte－Carlo simulation，the effects of different thickness and eccentricity for ellipse Co nanorings were studied.It was found that the stability of vortex－type states increases with increasing the thickness of ellipse Co nanorings when eccentricity was less.Moreover，the magnetic hysteresis loops of this system were similar to those of circular Co nanorings.However，there exists obvious difference between magnetic hysteresis loops of ellipse Co nanorings and those of circular Co nanorings when the eccentricity increased.The stability of vortex－type state was not significantly associated with the thickness.From the spin configurations，it was observed that there were more metastable states in the system of ellipse Co nanorings than those of circular Co nanorings.

ellipse Co nanorings;eccentricity;thickness;hysteresis loop;spin configuration

O 482.5

A

1007－7405(2012)05－0389－05

2012－05－25

2012－07－09

国家自然科学基金资助项目 (11004039，11004031);福建省自然科学基金资助项目 (2010J01277，2012J01003);福建省教育厅基金资助项目 (JA10086，JB11024);福建省大学生创新实验计划项目(Fjnu2011－004，BKL2011－010，cxxl－078)

叶晴莹 (1980—)，女，讲师，从事纳米磁性材料设计与理论计算研究，E－mail:qyye@fjnu.edu.cn.