改进的人工鱼群混合算法在智能组卷中的应用

吴 旭，洪联系，魏德志，郭剑平

(集美大学诚毅学院，福建厦门361021)

改进的人工鱼群混合算法在智能组卷中的应用

吴 旭，洪联系，魏德志，郭剑平

(集美大学诚毅学院，福建厦门361021)

现有的智能组卷多采用单一算法，而每种算法都有其各自的缺点，针对此缺陷提出了结合人工鱼群算法和遗传算法的优点组成混合智能组卷算法．在智能组卷开始时，采用人工鱼群算法快速靠近组卷目标，在组卷过程中，当最优个体在连续多个迭代过程中无变化或变化极小时采用遗传算法对人工鱼个体进行跳变，提高收敛速度．通过模拟计算证明，该混合智能算法能有效地优化其中单一算法独自进行智能组卷的成效．

智能组卷;人工鱼群;遗传算法;混合智能算法

0 引言

随着信息技术的发展，传统的人工组卷方式已经不能满足许多新出现的考核需求．例如，驾校理论考试机考、高校计算机等级考试机考、英语四六级机考、GRE机考和众多网络在线考试等．这些考试系统的共同特征就是题库量大、考核内容全面，在考核期间可随时无限量提供既符合考核指标要求又互不相同的试卷，具有随机性、科学性、合理性，尤其在交互式环境下可满足用户对组卷速度高的要求等．智能组卷问题实质上是一个多重约束条件的优化问题，目标的约束越多，问题的复杂度就越大．组卷过程是智能化、自动化的不断试探往复的过程．智能组卷主要有随机抽取法［1］、回溯法［2］、遗传算法［3］、模拟退火算法［4］、粒子群算法［5］等．在智能组卷研究起步早期较多采用随机抽取法、回溯法，目前智能组卷较多采用遗传算法、模拟退火算法、粒子群算法等．这些算法都存在约束条件的局部满足、参数不确定、组卷时间过长等问题．

人工鱼群算法 (AFSA)只需要比较目标函数值，具备对初值要求不高，可随机产生或设置固定值，收敛快等优点［6］．目前该算法已经由解决一维静态优化问题发展到解决多维动态组合优化问题，并在神经网络、电力系统、通风系统、油田定位、模糊控制器设计、灌区优化配水、数据挖掘、多用户检测、湖泊富营养综合评价、路由优化、任务调度和数字图像信号处理、非线性复杂函数最优化等方面得到了一定的应用，并取得了较好的应用效果．人工鱼群算法虽然具有上述的优良特性，但是人工鱼群算法前期搜索较快，后期较慢，且随着人工鱼数量增加，计算量相应增大，寻优精度难以提高［7］，因此也限制了单纯依靠人工鱼群算法行业应用的进一步发展．针对这个问题，研究者开始在人工鱼群算法中引入其他算法，利用不同算法的优势形成互补，从而较大地提高人工鱼群算法的效率．遗传算法 (GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，最初由美国Michigan大学J.Holland教授于1975年首先提出来［8］．遗传算法具有同时处理群体中的多个个体，覆盖面大，减少了陷入局部最优解的风险，利于全局择优，具有良好的自组织、自适应和自学习等优点．湖南农业大学的任剑等［10］设计了基于层次分析方法与人工鱼群算法相结合的智能组卷算法，主要通过层次分析法确定各组卷目标的权重，进而通过线性加权求和将多目标规划模型转换为单目标规划模型，最后利用改进的人工鱼群算法求解模型得到最优组卷方案;许昌学院的李娟等［11］采用基于人工鱼群模型的自动组卷抽题算法研究了智能组卷方式，并对鱼群的聚群追尾行为进行了改进．

人工鱼群算法和遗传算法的特性决定了其同样适合解决智能组卷的相关问题．采用人工鱼群与遗传混合算法进行人工智能组卷的研究目前还很少，但在其他领域已经有了一些应用．郭卫等［12］采用人工鱼群算法模拟梯级水库优化调度，再用遗传算法进行局部细化搜索，实例结果表明该混合算法行之有效．本文拟提出结合两种算法的优点来解决目前智能组卷中的算法缺陷，在组卷前期采用人工鱼群算法快速靠近组卷目标，当人工鱼群中的最优个体在连续迭代过程中没有变化或者变化较小时，采用遗传算法中的选择运算、交叉运算、变异运算实现人工鱼的跳变．

1 智能组卷数学模型的建立

智能组卷模型约束条件的目标函数如下．

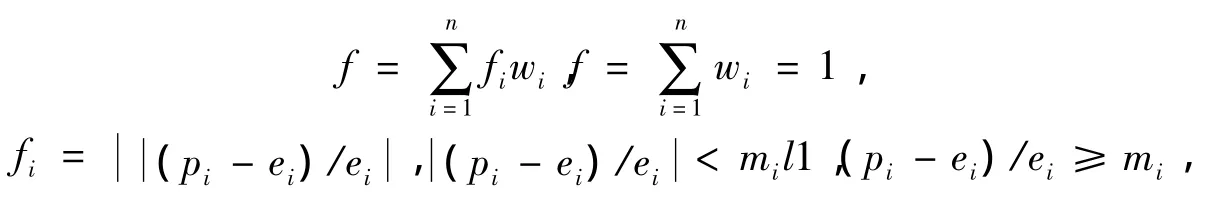
其中，fi代表第i个属性指标与用户指定指标的误差绝对值;wi代表不同属性在组卷中重要程度的权值;ei代表组卷各个目标的属性;mi代表允许误差范围．f的值越小，说明组卷结果越接近设定的目标要求．

各属性约束条件的设定如下．

1)总分约束条件S的值由教师设定，通常S=100．

2)各章节分约束条件SCk的值由教师设定．定义Cc为章节知识点覆盖率，Cc=试卷包含章节数/总章节数，C值约束条件由教师设定，一般情况Cc≥65%．

3)每种题型总分约束条件由教师设定．定义Cq为题型覆盖率，Cq=1．

4)各知识点总分SKk约束由教师设定．定义Ck为知识点覆盖率，Ck=试卷所包含知识点/考纲要求知识点数，一般设定Ck≥80%．

5)约束条件为各难度范围内的试题期望分值在教师限定范围内．

6)试卷区分度条件由教师设定．

7)考试时间T约束条件由教师设定，通常T=120 min．

2 人工鱼群算法与遗传算法的混合算法 (HIOA－GFA)

2.1 AFSA和GA的设计

2.1.1 AFSA的设计

人工鱼个体状态X=(x1，x2，…，xn)，其中xi(i=1，2，…，n)为寻优变量，人工鱼视野范围用Visual表示，人工鱼移动步长最大值用Step表示，拥挤度因子用δ表示．鱼群规模用Np表示．

1)觅食行为，可以认为鱼是通过感知水中的食物量或浓度来选择趋向的．在算法中表现为鱼经过试探，在人工鱼当前状态的d领域距离内搜索得到更优解，如果在次数k以内无法找到更优解则执行随机行为．

2)聚群行为，大量或少量的鱼都能聚集成群，用这种生存方式可以进行集体觅食和迷惑敌害．鱼聚群时所遵守的规则有三条，分别是分隔规则 (尽量避免与临近伙伴过于拥挤)、对准规则 (尽量与临近伙伴的平均方向一致)、内聚规则 (尽量朝临近伙伴的中心移动)．在算法中表现为，人工鱼在当前状态Xi的d距离领域内发现中心位置食物浓度更高且不太拥挤，则向中心位置移动．

3)追尾行为，当某一条鱼或几条鱼发现食物时，附近的鱼会尾随其后快速游过来，进而导致更远处的鱼也尾随过来．在算法描述中表现为鱼在当前状态的d距离领域内搜索最优解Xmax，如果对应位置的食物浓度Ymax更高且不太拥挤，则向该位置前进一步．

4)随机行为，鱼在水中悠闲的自由游动，基本上是随机的，其实也是为了在更大范围中寻觅食物或同伴．在算法中表现为鱼向任意方向前进一步．

5)使用公告板记录当前最优函数值．

6)鱼群经过觅食、聚群、追尾、随机行为选择后生成新鱼群．

终止条件判断，当达到最大搜索次数后取公告板值或公告板上函数值满足条件则停止搜索［13］．

2.1.2 GA的设计

一个生物种群是由经过基因编码的一定数目的个体组成．每个个体是带有特征染色体的实体．染色体作为遗传物质的主要载体决定了个体性状的外部表现．遗传算法采纳了自然进化模型如选择、交叉、变异、迁移、局域与临域等随机初始化生成一定数目个体种群，通过计算个体适应度，不断比较和优化个体产生新生代直至满足最优解．

1)初始化，设置进化代数计数器n=0，设置最大进化代数K，随机生成M个个体作为初始群体P(0)．

2)个体评价，计算群体P(t)中各个个体的适应度．

3)选择运算，将选择算子作用于群体．选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代．

4)交叉运算，将交叉算子作用于群体．所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作．

5)变异运算，将变异算子作用于群体，即对群体中的个体串的某些基因值作变动．

6)群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t1)．

终止条件判断，当达到最大搜索次数，则以进化过程中所得到的具有最大适应度个体作为最优解输出，或适应度函数值满足条件则结束运算输出对应解．

2.2 HIOA－GFA的编码

本混合算法是基于人工鱼群算法与遗传算法的混合算法．在人工鱼群算法运行到连续不变化或变化极小时将使用遗传算法进行收敛．由于遗传算法本身的生物学特性，使用二进制编码有利于遗传操作，所以本HIOA－GFA使用二进制编码形式．选中的题目用1表示，未被选中则用0表示．例如题库有10道题，其中6道被选中，分别是第1、3、4、6、8、9道试题，则该份试卷二进制编码为1011010110．采用人工鱼群算法运行时，将每一套生成的试卷视作为一条候选鱼．采用遗传算法运行时，将每一套生成的试卷视作为一个染色体．

2.3 HIOA－GFA的组卷流程

1)初始化公告板．根据满足分数、题型、二项基本要求随机产生n条鱼．

组卷时，可首先设置为生成仅满足分数为100分，题型覆盖单选、多选、判断、问答、设计5个题型的 n条鱼，即 n套如下试卷:X1=001010111000…1，X2=110001000110…0，……，Xn=011000110111…1．

不采用完全随机生成初始鱼群是因为这样可以加快鱼群收敛速度;设置4个参数，分别是stopIterate代表人工鱼状态连续不变化或变化很小时的迭代次数，初始值为0;maxStopIterate代表鱼群最大允许连续不变化次数;iterateNum代表遗传操作迭代次数计数器，初始值为0;maxIterateNum代表遗传操作最大允许迭代次数．最后设置人工鱼的相关参数如Visual(可视域)、Step(步长)、δ(拥挤度因子)、tryNum(试探次数)等．

2)计算初始鱼群各个体当前状态值，选取最小值的鱼进入公告板，并把该人工鱼状态值赋予公告板．

组卷时，由计算机分别计算出这n套试卷的目标函数f值，并将f值最小的那套试卷所对应的二进制编码存入字符串变量bestFish，同时将最小的f值赋予变量board，即记录到公告板．

3)根据人工鱼群算法进行追尾、聚群、觅食行为或随机行为的选择．如果行为选择之后，最小值无变化，则人工鱼再进行随机行为，并且设置stopIterate=stopIterate+1．

组卷时，追尾活动表现为每条鱼Xi即每套二进制编码试卷查看在自己Visual(可视域)范围内的其他二进制编码试卷，从中找出目标函数值f最小的试卷Xj，对应目标函数值f记为Yj．Xj周围在可视域内其他试卷数量记为nf．若Yj*nf＜δ(拥挤度因子)*Yi，则认为Xj周围“食物”较多而且不太拥挤，这个时候试卷Xi可以对自己和试卷Xj的不同位进行重新随机取值，比如Xi=0011001，Xj=0010100，则把Xi的第四、第五和第七位随机取值，从而使得Xi向Xj靠近．

在追尾失败的情况下，聚群行为表现为每条鱼Xi，即每套试卷找出自己可视域内的其他试卷，形成小鱼群，然后找出所在鱼群中心点．找寻中心点具体表现为若鱼群中半数以上试卷在第i位上取1，则中心点第i位也是1，否则设置为0．之后方式采用追尾行为中判断食物浓度和拥挤度来决定是否向中心点靠近．

在聚群失败的情况下进行觅食活动，即每套试卷随机从自身选取visual(可视域)个位，并对所选取的这些位进行随机变换，若新状态更优则向新状态移动，否则重新进行觅食，重复tryNum(尝试次数)次后依然没有更优则进行随机移动．

4)各人工鱼行为选择后比较自身f值和公告板board的值，如果f值优于公告板board值，则用对应试卷编码取代bestfish，同时用自身f值更新公告，设置stopIterate=0．

5)判断stopIterate的值是否等于maxStopIterate．如果两者值相等，执行遗传操作，即跳转到6)．否则判断算法终止条件，即跳转到7)．

6)除公告板上人工鱼外，进行遗传操作．将鱼群进行适应值降序排序．首先，选择适应值前30%的染色体直接进入子代;其次，选择接下来69%的染色体进行单点杂交;最后，选择尾部1%的染色体进行变异操作．计算新生成的各染色体个体值，并比较公告板，如果优于则取代;设置stopIterate=0．

7)判断是否满足算法终止条件，即iterateNum的值是否等于maxIterateNum的值，如不满足则设置iterateNum=iterateNum+1，并且跳转到3)执行．满足则结束算法运行，输出公告板上的最优解［7］．

算法流程图如图1所示．

图1 HIOA-GFA流程图Fig.1 Flow chart for the HIOA-GF

3 HIOA－GFA实验分析

3.1 实验条件及算法参数设定

为了验证HIOA－GFA算法的可行性和有效性，利用现有《大学计算机应用基础》题库中1500套题目进行组卷实验．该题库包含了选择题、填空题、判断题、程序设计题、问答题等，每组试卷总分100分，考试时间120 min，试卷难度系数0.5．

实验环境为Windows xp操作系统，CPU为Inter Core 2 Duo 2.4G主频，2G内存，Visiual Studio 2008环境下C#语言编程实现，数据库使用SQL SERVER 2005．

HIOA－GFA参数设定为群体规模Np为30，AFSA中最大连续不变化次数maxStopIterate=10，视野Visual=4，步长Step=1，拥挤度因子δ=6，试探次数tryNum=3．GA中最大迭代次数maxIterate-Num=120．遗传操作中选择概率yc=0.30、交叉概率ym=0.69、变异概率yv=0.01．

抽题模型参数如表1所示．

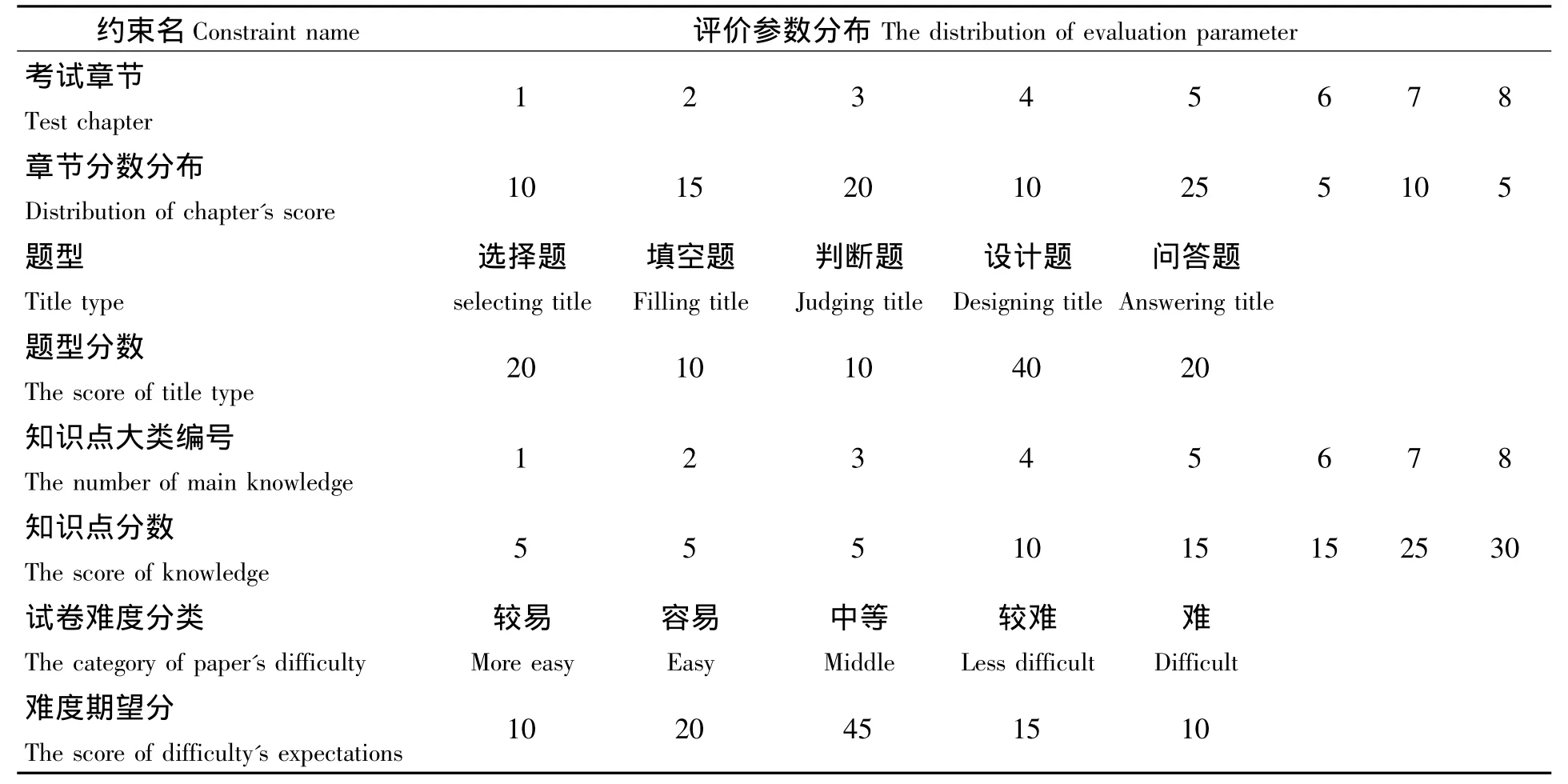
表1 抽题模型参数Tab．1 Parameters for the extracting －title model

3.2 实验结果

依据上述组卷要求，采用随机抽取法 (SSA)、人工鱼群算法 (AFSA)、遗传算法 (GA)、人工鱼群与遗传混合算法 (HIOA－GFA)4种组卷算法进行对比实验，对题库为1500道题分别组卷20次，4类成功率对比如图2所示，平均耗时对比如图3所示．

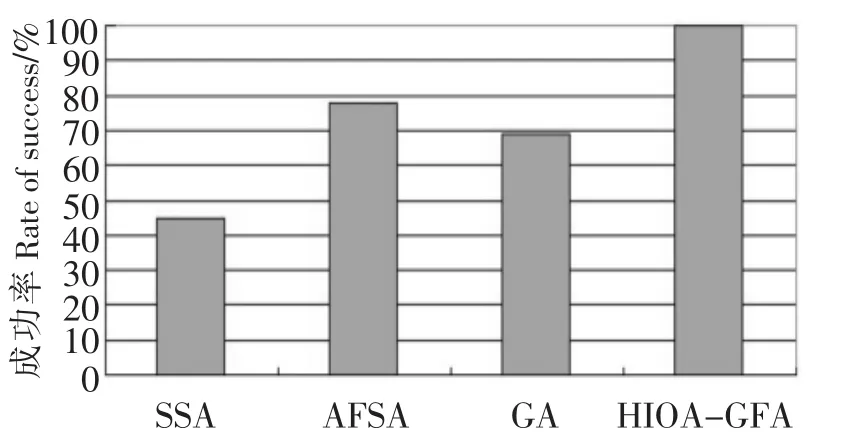
图2 4种算法20次组卷成功率对比图Fig.2 The success rate's comparison chart for using the four algorithms to test papers 20 times

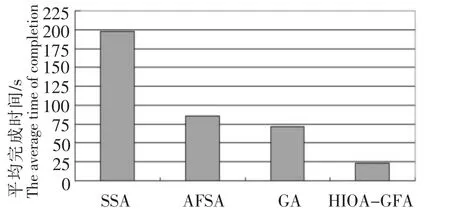
图3 4种算法20次组卷平均耗时对比图Fig.3 The average time-consuming comparison chart for using the four algorithms to test papers 20 times

3.3 结果分析

3.3.1 算法有效性分析

从图2对比数据看出，随机抽取算法在题库量大时，成功率明显偏低，在本案例中只有45%．单独采用人工鱼群算法和遗传算法成功率分别提高至78%和69%，但是成功率依然不高．采用HIOA－GFA进行组卷，成功率达到了100%．所以采用HIOA－GFA组卷可以很好地满足用户的组卷需求．

3.3.2 算法组卷效率分析

从图3对比数据看出，随机抽取法组卷速度慢，平均每次组卷耗时198 s．单独采用AFSA或GA组卷，效率有所提高，但是时间消耗依然较长，不能够很好满足用户需要．采用HIOA－GFA进行组卷，时间则大为缩短，耗时分别只有前3种算法的11.6%，26.7%，31.9%．因此可以看出，采用HIOA－GFA进行智能组卷可以快速提高组卷速度．

［1］王萌，金汉均，王晓荣，等．集合随机抽选法在智能组卷中的研究 ［J］．计算机工程与设计，2006，27(19):3584－3585．

［2］王文发，马燕，李宏达．回溯法求解多约束分配问题［J］．江西师范大学学报:自然科学版，2008，32(6):729－732．

［3］张琦，郑河荣，刘志．基于优化遗传算法的智能组卷系统研究［J］．浙江工业大学学报，2009，37(3):307－310．

［4］周艳聪，刘艳柳，顾军华．小生境自适应遗传模拟退火智能组卷策略研究［J］．小型微型计算机系统，2011，32(2):323－326．

［5］阎峰，安晓东．基于粒子群优化算法的智能抽题策略研究［J］．中北大学学报:自然科学版，2008，29(4):334－337．

［6］李广水，马青霞，陈爱萍，等．分布式遗传算法在智能组卷中的Web services实现 ［J］．计算机应用研究，2010，27(11):4185－4186．

［7］张汉强．人工鱼群混合智能优化算法及其应用研究［D］．浙江:浙江工业大学控制系，2010．

［8］周艳丽．基于改进遗传算法的自动组卷问题研究 ［J］．计算机仿真，2010，27(9):320－321．

［9］黄艳峰，陈涛．基于改进遗传算法的智能组卷系统的设计与实现 ［J］．煤炭技术，2009，28(10):150－151．

［10］任剑，卞灿，全惠云．基于层次分析方法与人工鱼群算法的智能组卷 ［J］．计算机应用研究，2010，27(4):1293－1300．

［11］李娟，田胜利．基于人工鱼群模型的自动组卷抽题算法研究 ［J］．许昌学院学报，2008，27(5):92－97．

［12］郭卫，方国华，黄显峰．基于人工鱼群遗传算法的梯级水库优化调度研究 ［J］．水电能源科学，2011，29(6):49－51．

［13］张梅凤．人工鱼群智能优化算法的改进及应用研究［D］．大连:大连理工大学电子与信息工程学院，2008．

(责任编辑 朱雪莲 英文审校 黄振坤)

Improved AFSA for Solving Intelligent Test Problem

WU Xu1，HONG Lian-xi2，WEI De-zhi3，GUO Jian-ping4
(Chenyi College，Jimei University，Xiamen 361021，China)

Intelligent auto－generating paper was a optimization problem which had multi－target parameter in certain constraint conditions．There had been many algorithms to realize intelligent auto－generating paper．But，most of the methods achieving the target used only a single algorithm．Since each of the algorithm had its own shortcomings，so in the process of intelligent auto －generating paper，it sometimes can't avoid the defects of a single algorithm．By incorporating AFSA and GA's advantages into a mathematical model for intelligent auto-generating paper，a HIDA algorithm was proposed．In the course of generating paper，the AFSA was adopted to approach to the target first．When the best individual didn't change or changed very small continually，the GA was used to make the fish jump to increase the convergence speed．The results of experiments showed that the HIOA －GFA was better than single one of the Algorithms to generate paper．

intelligent auto－generating paper;AFSA;GA;HIOA

TP 301.6

A

1007－7405(2012)05－0394－07

2012－01－18

2012－06－10

集美大学诚毅学院重点教学改革基金资助项目 (P10222)

吴旭 (1981—)，男，实验师，硕士，主要从事智能算法、网络安全、云计算等方向研究．