一种单通道的源数盲估计方法

王荣杰，詹宜巨，周海峰

(1．集美大学轮机工程学院，福建厦门361021;2．中山大学工学院，广东广州510006;3．中山大学信息科学与技术学院，广东广州510006)

一种单通道的源数盲估计方法

王荣杰1，3，詹宜巨2，周海峰1

(1．集美大学轮机工程学院，福建厦门361021;2．中山大学工学院，广东广州510006;3．中山大学信息科学与技术学院，广东广州510006)

针对单通道的源数盲估计技术，提出了一种基于经验模态分解和交叉验证技术相结合的源数估计方法，该方法首先通过经验模态分解技术将单通道的观测信号转换为虚拟的多通道观测信号，然后采用基于交叉验证技术来确定混合在单通道中的源信号个数．仿真实验结果表明:该方法能准确地估计出混合在单通道中服从超高斯分布、亚高斯和高斯分布的源信号个数．

单通道;源数;盲估计;经验模式分解;交叉验证

0 引言

盲源分离 (Blind Source Separation，BSS)是近年发展起来的一种新的信号处理方法．所谓的盲源分离，就是在源信号和混合系统 (或传输通道)等未知的情况下，仅根据源信号的统计特性，由观测到的混叠信号恢复出源信号，鉴于其优越的假设模型，它被广泛用于数字通信、语音、图像处理、故障诊断和生物医学信号处理等领域［1－5］．根据观测信号和源信号的个数，盲源分离可分为超 (正)定盲源分离和欠定盲源分离，而单通道盲源分离是一种特殊的欠定盲源分离．在盲源分离过程中，正确的源信号个数是良好的源信号恢复质量的先决条件;相比之下，欠定情况下的源数估计不如超 (正)定情况下的源数盲估计技术成熟，而单通道欠定情况下的源数估计技术是本文的研究重点．目前，单通道源信号个数的盲估计尚处于初探阶段，很多关于单通道盲源分离的文献都假设源信号个数为已知，但在实际中是未知的［6－7］;虽然文献 ［4，8］中提及源信号个数盲估计的方法，但是它们都以源信号分布的频段已知作为前提，这在实际中也是不可行的．本文提出了一种无需依赖源信号任何已知条件的源数盲估计方法，该方法首先利用经验模态分解 (Empirical Mode Decomposition，EMD)构造观测信号的虚拟通道，即将单通道的混合信号虚拟成超 (正)定情况，然后再通过一种基于交叉验证的技术来确定源信号的个数．

1 问题的描述

假设n个彼此相互独立的未知源信号s(t)=［s1(t)，s2(t)，……，sn(t)］T，通过一未知瞬时线性混合系统后，得到m个观测信号x(t)=［x1(t)，x2(t)，……，xm(t)］T．观测信号x(t)与源信号s(t)的关系可由式 (1)表示．

式中，A∈Rm×n为混合矩阵，它反映了混合系统或信道的传输特性，t=0，……，N－1为时域采样点．当m≥n时为超 (正)定情况，而当m＜n时为欠定情况;单通道源信号个数的盲估计就是在m=1的欠定情况，仅根据已知的x(t)对s(t)源信号的个数进行估计．

2 基于EMD的单通道源数盲估计

考虑到经验模态分解能根据信号本身的特点，自适应地将信号分解为若干个独立的固有模态函数(Intrinsic Mode Function，IMF)之和;本文首先利用EMD技术将观测信号由一维变化到高维，有效地解决单通道的欠定问题;然后采用一种基于交叉验证技术的方法来估计单通道情况下的源信号个数．

2.1 EMD分解原理

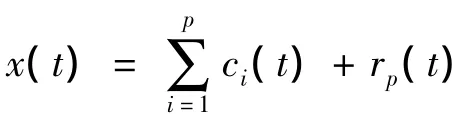
2.2 基于EMD的单通道源数盲估计

交叉验证是一种多变量统计技术，它的思想是将数据分成几部分，其中取一部分提取数据的特征，其他部分用于验证这些特征［11］．令观测信号x(t)的EMD分解得到的IMF分量ci和rp组成的多维观测信号向量为y(t)，即y(t)=［c1(t)，c2(t)，……，cp(t)，rp(t)］T;利用交叉验证技术的思想，式 (2)给出了一种新的源信号个数估计准则．

其中:

式 (2)中的trace(·)为矩阵求秩运算;式 (3)中的C为Y的协方差矩阵为对角元素为C前i个特征值的对角矩阵，Ui的列向量为与其相应的特征向量．注意，式 (2)中计算，对角矩阵的对角线与Λp+1是交叉的，且两个矩阵在对角线上的元素排序是相反的;可视为交叉验证技术中提取数据的特征，而可视为用于验证的特征，因此可以利用此原理来确定单通道的源数．

基于EMD的单通道源数估计的实现步骤:首先，由EMD对单通道的观测信号进行分解，获得IMF分量ci(t)和残余函数rp(t);然后将IMF分量和残余函数组成为新的多维观测信号向量为y(t);最后分别计算i=1，…，p+1的Ψ(i)，估计的源数n由式 (2)确定．

3 仿真实验分析

为了验证基于EMD的单通道源数盲估计方法的有效性，分别对服从亚高斯分布、超高斯分布的源信号以及亚高斯、超高斯和高斯混合的源数盲估计进行了仿真实验．在仿真实验中，式 (1)中的混合矩阵A都是在［－1 1］之间随机产生．

3.1 源信号为亚高斯的源数估计实验

在这个仿真实验中，首先采用两个源信号的表达式见式 (4)，其波形如图1a所示;混叠矩阵A的值见式 (5)，其混合后的波形如图1b所示，图1c所示为它的EMD分解信号．为了进一步评价本文提出算法对亚高斯信号的源数盲估计性能，笔者对图2a所示的源信号进行仿真实验，其中s3为高斯白噪声信号，它是由randn函数产生的，这三个源信号经式 (6)中的A混合得到的观测信号如图2b所示，它的EMD分解信号如图2c所示．这两种情况下的源数盲估计结果如表1所示．说明:CR为交叉验证系数;E1为源信号服从亚高斯分布的仿真实验，E2为源信号服从亚高斯和高斯分布的仿真实验;在该仿真实验中源信号s1、s2和s3的峭度分别为－1.5006、－1.4988和0.0797．

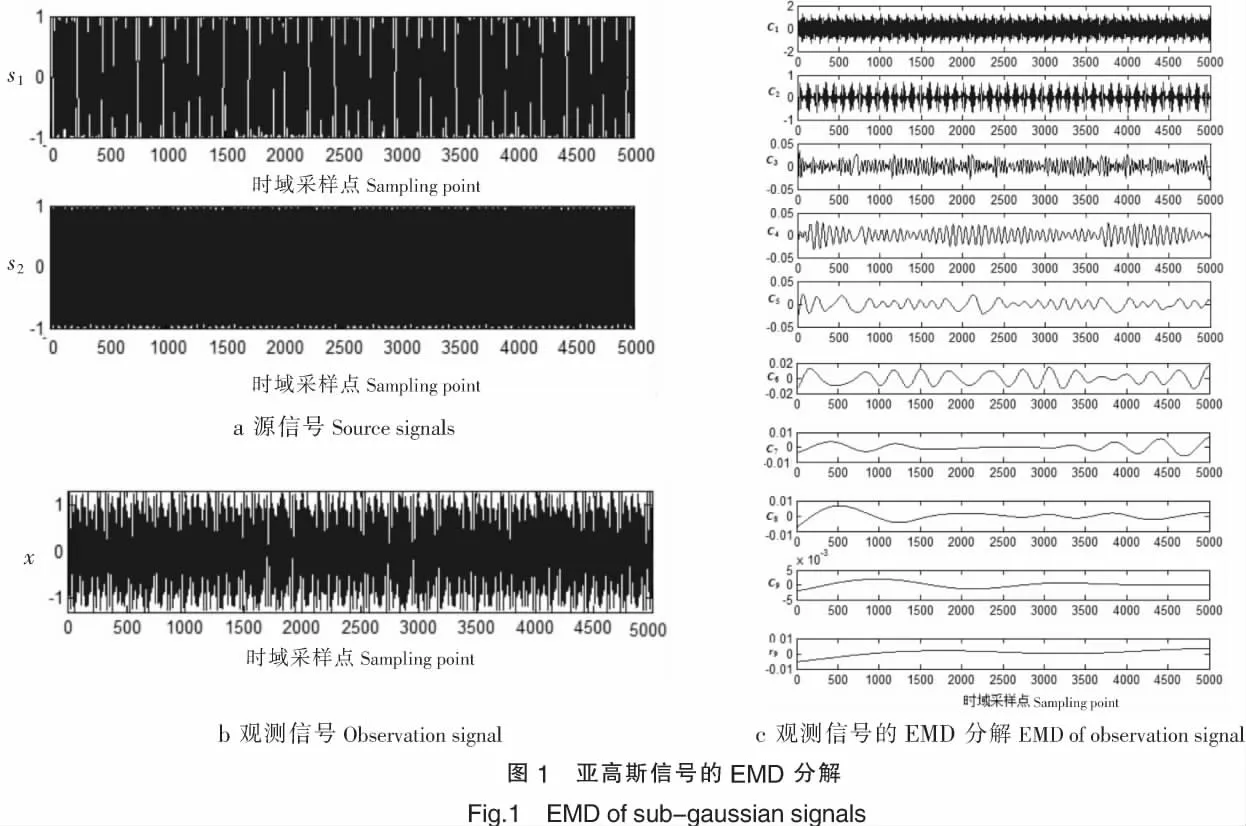
表1 源信号为亚高斯的源数估计结果Tab.1 Result of estimation number of sub－gaussian sources

3.2 源信号为超高斯的源数估计实验

在这个仿真实验中，超高斯分布的源信号取自文献 ［12］，其波形如图3a所示，它们的峭度分别为5.0720和3.9000;而s3仍为图2(a)所示的高斯白噪声信号，源信号经式 (6)中的A混合后得到的信号如图3b所示，表2所示为它的源数盲估计结果．

表2 源信号为超高斯的源数估计结果Tab.2 Result of estimation number of super－gaussian sources

3.3 超高斯、亚高斯和高斯源信号混合的源数估计实验

在这个仿真实验中，4个源信号如图4a所示，s1和s2为服从亚高斯分布的源信号，s3和s4分别为服从超高斯和高斯分布的源信号;混叠矩阵A的值见式 (7)，混合信号如图4b所示，表3所示它的源数盲估计结果．

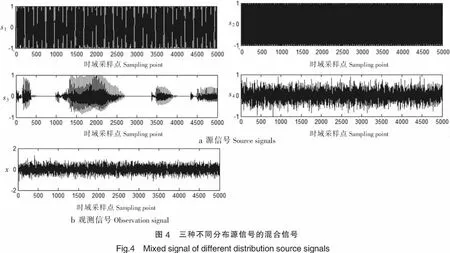
表3 源信号为三种不同分布源信号的源数估计结果Tab.3 Result of estimation number of different destruction sources

由亚高斯、高斯和超高斯信号的源数估计实验结果可知，对单通道的观测信号进行EMD可以将欠定的源数估计问题虚拟成超定的源数估计问题，即解决了单通道的欠定问题;根据式 (2)—式(3)的原则，确定表1、表2和表3中的源信号个数分别为2，3，3，4;由此可表明本文提出的基于交叉验证技术的源数估计方法能准确估计出混合在单通道中的服从超高斯、亚高斯和高斯分布的源信号个数．

4 结语

为了估计单通道的源数，本文提出了一种基于经验模态分解和交叉验证技术相结合的源数估计方法，该方法首先通过EMD分解将单通道的观测信号虚拟为超正定的观测信号，它克服了单通道的维数欠定的限制，然后采用超正定下基于交叉验证估计法确定混合在单个通道中源信号的个数．仿真结果表明了基于EMD和交叉验证技术相结合的盲估计方法可以应用于准确确定单通道的源信号个数．

［1］BAI E W，LI Q Y，ZHANG Z Y．Blind source separation/channel equalization of nonlinear channels with binary inputs［J］．IEEE Transaction on Signal Processing，2005，53(7):2315 －2323．

［2］ ARAKI S，MAKINO S，BLIN A．Underdetermined blind separation for speech in real environment with sparseness and ICA ［C］ //Processing of ICASSP ’04．Canada:Montreal，2004:881－884．

［3］ ANNA T，LUIGI B，EMANUELE S．A markov model for blind image separation by a mean－field EM algorithm ［J］．IEEE Transactions on Image Processing，2006，15(2):473－482．

［4］ HONG H B，LIANG M．Separation of fault features from a single－channel mechanical signal mixture using wavelet decomposition ［J］．Mechanical Systems and Signal Processing，2007，21(5):2025－2400．

［5］TEIXEIRA A R，TOM A M，LANG E W．Automatic removal of high－amplitude artefacts from single－channel electroencephalograms［J］．Computer Methods and Programs in Biomedicine，2006，83(2):125－138．

［6］ MA H G，JIANG Q B，LIU Z Q．A novel blind source separation method for single－channel signal［J］．Signal Processing，2010，90(12):3232－3241．

［7］ JANG G J，LEE T W，OH Y H．Single channel signal separation using MAP－based subsapce decompostion ［J］．Electronics Letters，2003，39(24):1766－1767．

［8］BOGDAN M，MAARTEN D V，IVAN G．Source separation from single－channel recordings by combining empiricalmode decompostion and independent compoenent analysis［J］．IEEE Transactions on Biomedical Engineering，2010，57(9):2188－2196．

［9］ HUANG N E，SHEN Z，LONG S R．The empirical mode deecomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis［J］．Proceedings of the Royal of London Series A，1998，454(1971):903－995．

［10］徐亮，成谢峰．一种单路混沌信号盲源分离方法 ［J］．安徽师范大学学报:自然科学版，2010，33(1):28－33．

［11］王荣杰，詹宜巨，周海峰．船舶噪声的自适应分离技术 ［J］．中国航海，2011，34(3):10－15．

［12］ CICHOCKI A．ICALAB Toolboxes［EB/OL］．［2007－03－28］．http://www．bsp．brain．riken．jp/ICALAB/ICALABSignalProc/benchmarks．

(责任编辑 陈 敏 英文审校 黄振坤)

A Method of Blind Source Numbers Estimation of Single－channel

WANG Rong-jie1，3，ZHAN Yi-ju2，ZHOU Hai-feng1
(1．Marine Engineering Institute，Jimei University，Xiamen 361021，China;2．School of Engineering，Sun Yat－sen University，Guangzhou 510006，China 3．School of Information Science and Technology，Sun Yat－sen University，Guangzhou 510006，China)

A method based on empirical mode decomposition and cross validation presented for the blind source numbers estimation under single－channel case，in which empirical mode decomposition used to change observation signals of single－channel into observation signals of multi－dimension channel，then the source numbers estimated according to the principle of cross validation．The simulation results show the proposed method can estimate numbers of those source signals of Gaussian，super－ and sub－Gaussian distribution which are mixed into single－channel．

single－channel;number of sources;blind estimation;empirical mode decomposition;cross validation

TN 911.7

A

1007－7405(2012)04－0315－07

2011－09－30

2012－02－25

国家自然科学基金项目 (51179074，61172156);广东省科技计划项目 (2009390004202223)

王荣杰 (1981—)，男，讲师，博士生，从事智能信息处理和电力电子电路故障诊断研究．