Minty型含参数拟变分锥的稳定性

陈建弘，黄龙光

(集美大学理学院，福建厦门361021)

Minty型含参数拟变分锥的稳定性

陈建弘，黄龙光

(集美大学理学院，福建厦门361021)

通过集值映射的各种上、下半连续性，研究一类参数拟变分锥的Minty型类似不等式的解集特征，给出其解集，近似解集的上、下半连续的充分性条件，进而研究Minty型含参数拟变分锥的稳定性，并通过建立近似解集的上半连续的充分条件给出拟变分锥优化问题解的刻画．

拟变分锥;稳定性;连续性;闭性

0 引言

含参数变分不等式在优化问题和经济均衡理论中有重要作用，为此，人们不遗余力地加深和拓展它的内涵和外延:Minty［1］提出经典Minty含参数不等式问题;Fan等［2］探讨含参数广义变分不等式的Stampacchia和Minty型的解集的稳定性问题;Khanh等［3］研究解集、近似解集的半连续问题．虽然拟变分不等式很早就被提出，并在经济、工程等各方面都有广泛应用［4－5］，但是Minty型含参数拟变分不等式的解集稳定性方面目前尚未进行系统研究．文献［6］仅探讨数值函数的含参数拟变分不等式的稳定性问题，本文主要在锥条件下研究Minty型含参数拟变分的解的稳定性问题．

设E与A分别是赋范空间X与Y中的非空闭子集与非空闭凸子集，C是Y中的闭凸尖锥，K:E×Y→2Y与T:E×Y→2L(Y，Y)是集值映射．dom K={(x，y)∈E×Y:K(x，y)≠Ø}．本文研究下列问题:对x0∈E，找u0∈K(x0，u0)∩A ，使得(MVI(x0))〈t，u0－v〉∈－C ，∀v∈K(x0，u0)，∀t∈T(x0，v)．本文总设M(x0):={u∈K(x0，u0)∩A，〈t，u0－ v〉∈－ C，∀v∈K(x0，u0)，∀t∈T(x0，v)}≠ Ø ．

1 解集的上半连续性

定义1［6－7］集值映射F在x0∈F是B－usc当且仅当对任意开集N，满足F(x0)⊂N，存在δ＞0，使得对任意的x∈B(x0，δ)，有F(x)⊂N;集值映射F在x0∈F是B－lsc当且仅当对任意开集N，满足F(x0)∩N≠Ø，存在δ＞0，使得对任意的x∈B(x0，δ)，有F(x)∩N≠Ø．

定理1 对于x0∈E，如果:ⅰ)K在{x0}×Y是闭的，并且是B－lsc;ⅱ)T在{x0}×Y是B－lsc;ⅲ)A是Y的紧子集，那么M在x0是B－usc［6］且是闭的，同时M(x0)是紧的．

证明 假设M在x0不是B－usc，则存在一开集V，满足M(x0)⊂V，使得对任意的序列xn→x0，存在un∈M(xn)但un∉V，对任意n．由于un∈K(xn，un)∩A，A是紧的，不失一般性，假设un→u0∈AV．由于K在{x0}×Y是闭映射，可得u0∈K(x0，u0)．由un∈M(xn)，有

下证u0∈M(x0)．反之，若u0∉M(x0)，那么存在v0∈K(x0，u0)，t0∈T(x0，v0)，使得

由K 在 (x0，u0)是 B －lsc，v0∈ K(x0，u0)，(xn，un)→(x0，u0)，存在 vn∈K(xn，un)使得 vn→v0．类似地，由 T在 {x0}×Y是B －lsc，t0∈K(x0，v0)，(xn，vn)→(x0，v0)，存在 tn∈T(xn，vn)使得 tn→t0．在式 (1)中取v=vn，t=tn，且令n→∞，取极限有

与式 (2)矛盾．因此，u0∈M(x0)⊂V，与un→u0∈AV矛盾，故M在x0是B－usc的．

为了证明M(x0)是紧的，先证明M(x0)是闭集．若M(x0)不是闭集，则存在un∈M(x0)，使得un→u0，u0∉M(x0)．由于K在{x0}×Y是闭映射，因此 u0∈ K(x0，u0)．同样，由于u0∉M(x0)，存在v0∈K(x0，u0)，t0∈T(x0，v0)，使得式 (2)成立．另外，类似上面的证明又可得式(3)成立，同样与式 (2)矛盾．此外，由于M(x0)⊂A，A是紧的，可推得M(x0)是紧的．由文献［8］可推得M在x0是闭的．

下面结论表明用序列方式取代K，T在{x0}×Y是B－lsc，定理1仍然成立．

定理2 对于x0∈E，如果:ⅰ)K在{x0}×Y是闭的;ⅱ)A是Y的紧子集;ⅲ)∀u0∈K(x0，u0)∩ A，∀(xn，un)→(x0，u0)，

可推得存在一正整数n，使得〈t，un－v〉∉－C，对某v∈K(xn，un)，t∈T(xn，v)，那么M在x0是B－usc且是闭的，同时M(x0)是紧的．

证明 假设M在x0不是B－usc，则存在一开集V，满足M(x0)⊂V，使得对任意的序列xn→x0，存在un∈M(xn)但un∉V，对任意n．由于un∈K(xn，un)∩A，A是紧的，不失一般性，假设un→u0∈AV．由于K在{x0}×Y是闭映射，可得u0∈K(x0，u0)．由un∈M(xn)有

可得u0∈M(x0)．反之，若u0∉M(x0)，那么〈t0，u0－v0〉∉－C，对v0∈K(x0，u0)，t0∈T(x0，v0)．由于(xn，un)→(x0，u0)，由条件ⅲ)的假设，则存在 n使得〈t，un－v〉∉－C，对 v∈ K(xn，un)，∀t∈T(xn，v)，这与式 (5)矛盾．因此，u0∈M(x0)，与un∉V(n任意)矛盾．M(x0)是紧的，M在x0是闭的证明与定理1证明类似．

注1 容易看出，定理1中K，T是B－lsc，可以推出定理3ⅲ)．事实上定理3ⅲ)是更一般的条件，通常用来取代映射K和T的连续假设．这表明如果式 (4)对v0∈K(x0，u0)，t0∈T(x0，v0)成立，那么对v∈K(xn，un)，t∈T(xn，v)至少有一系列(xn，un)→(x0，u0)使式 (4)也成立．

关于近似解集，有与定理1、定理2类似的以下两个定理．

定理3 对x0∈E，如果满足定理1的条件，那么对任意在x0是B－usc且闭的，同时对任意是紧的．

定理4 对x0∈E，如果满足定理2ⅰ)、ⅱ)的条件，如果∀u0∈K(x0，u0)∩A，∀(xn，un)→，对 v0∈K(x0，u0)，t0∈T(x0，v0)，存在一正整数n，使得〈t，un－对 v∈ K(xn，un)，t∈ T(xn，v)，那么在 x0是 B －usc且闭的，同时是紧的．

2 解集的下半连续性

下面通过适当的条件讨论解集的下半连续性及建立涉及映射K和T的序列条件．

定理5对于x0∈E，如果:ⅰ)在x0是B－lsc，K(x0，u0)∩A ，∀(xn，un)→(x0，u0)，〈t，u0－ v〉∈－ C ，∀v∈K(x0，u0)，∀t∈T(x0，v)，可推得存在一正整数n，使得〈t，un－v〉∈－C，∀v∈K(xn，un)，∀t∈T(xn，v)，那么M在x0是B－lsc．

证明 假设M在x0不是B－lsc，则存在E中一序列{xn}，xn→x0，u0∈M(x0)，使得对任意序列由于在x0是，则存在一序列un→u0．由上面的假设，不失一般性，如果，那么

由于 un∈M(x0)，使得〈t，u0－ v〉∈－ C ，∀v∈ K(x0，u0)，∀t∈ T(x0，v)．由于 (xn，un)→ (x0，u0)，由条件ⅱ)的假设，存在 n，使得〈t，un－ v〉∈－ C，∀v∈ K(xn，un)，∀t∈ T(xn，v)，这与式(6)矛盾．

下面给出映射－T的广义单调可建立解集的下半连续性的条件．

定义2 F是集值映射，ⅰ)称F在X上是伪单调当且仅当对任何x，x0∈X，〈ξ，x－x0〉∈C，ξ∈F(x0)⇒ ＜η，x－x0＞∈C，∀η∈F(x);ⅱ)称F在X上是拟单调当且仅当对任何x，x0∈X，x≠x0，〈ξ，x－x0〉∉－C，ξ∈F(x0)⇒〈η，x－x0〉∈C，∀η∈F(x)．

定理6 对于x0∈E，假设定理1的条件成立，且:ⅰ)对任意的u0∈M(x0)，〈t，u0－v〉∉C．∀v∈M(x0){u0}，t∈T(x0，v);ⅱ) －T在{x0}×Y是拟单调的，则M在x0是B－lsc．

证明 假设M在x0不是B－lsc，则存在E中一序列{xn}，xn→x0，u0∈M(x0)，使得对任意序列un∈M(xn)，unu0．由于un∈A，A是Y的紧子集，不失一般性，假设un→u'∈A．由定理2可得u'∈ M(x0)．由上面的假设有 u0≠u'．由 u0，u'∈M(x0)和条件ⅰ)得:〈t'，u0－u'〉∉－C，t'∈－ T(x0，u')，〈t0，u0－ u'〉∉ C，t0∈－T(x0，u0)，这与 －T是拟单调矛盾．

定理7 对于x0∈E，假设定理1的条件成立，且:ⅰ)对任意的u0∈M(x0)，〈t，u0－v〉∈－C．∀v∈M(x0)，t∈T(x0，v);ⅱ) －T在{x0}×Y是伪单调的;ⅲ)〈t，u－v〉=0，∀t∈T(x0，u)∪T(x0，v)⇒u=v，则 M 在 x0是 B －lsc．

证明 由定理6的前半部分证明有u0≠u'．由u0，u'∈M(x0)和条件ⅰ)得

由于－T是伪单调的，由式 (7)和式 (8)分别得〈t0，u0－u'〉∈C和〈t0，u'－u0〉=0．由条件ⅲ)有u0=u'，导致矛盾．

3 具拟变分锥条件的优化问题解的稳定性

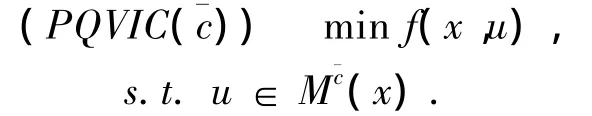
观察上面的近似解集的稳定性，可提供一个条件确保上半连续．

定理8 如果定理1的条件成立，并且:ⅰ)E是Rn的有界子集;ⅱ)f是下半连续，那么∀δ≥0，Ωδ在=0时是 B －usc的．

证明 令δ∈C是固定的．假设Ωδ在=0时不是B－usc的，则存在一开集V，满足Ωδ(0)⊂V，使得对任意的序列，存在但，对任意 n．由可得对

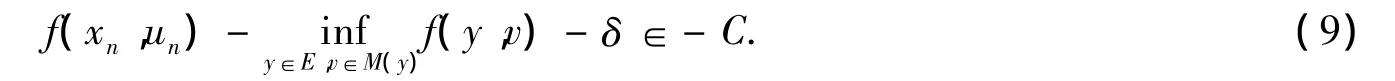
由定理1条件ⅰ)，不失一般性，假设(xn，un)→(x0，u0)，类似于定理1的证明有u0∈M(x0)．由f是下半连续和式 (9)，有．再由u0∈M(x0)可得(x0，u0)∈Ωδ(0)⊂V，与对任意n，(xn，un)∉V矛盾．

推论1 如果定理1的条件ⅰ)、条件ⅱ)满足，并且:ⅰ)存在d∈int C，δ≥0，使得Ωδ(d)有界;ⅱ)f是下半连续的，那么∀δ≤δ'，Ωδ在时是B－usc的．

证明 假设Ωδ在不是B－usc的，对δ≤δ'，则存在一开集V，满足Ωδ(0)⊂V使得对任意的序列，存在但 (xn，un)∉V ，对任意 n．由于对，存在一正整数m，使得不失一般性，假设(xn，un)→(x0，u0)．由，对，有．再类似定理8的证明可知定理9成立．

定理9 如果定理2的条件成立，并且:ⅰ)E是Rn的有界子集;ⅱ)f是下半连续，那么∀δ≥0，Ωδ在时是 B －usc的．

注2 由于Ωδ在时是B－usc的，不论是定理8还是推论1的条件，Ωδ在时是B－连续［6］的．

［1］ MINTY G J．On the generalization of a direct method of the calculus of variation ［J］．Bull Am Math Soc，1967，73:315-321．

［2］ FAN J H，ZHONG R Y．Stability analysis for variational inequality in reflexive Banach space ［J］．Nonlinear Anal，2008，69(8):2566-2574．

［3］KHANH P Q，LUU L M．Lower semicontinuity and upper semicontinuity of the solution sets and approximate solution sets of parametric multivalued quasivariational inequalities［J］．J Optim Theory Appl，2007，133(3):329-339．

［4］ CHAN D，PANG J S．The generalized quasivariational inequality problem ［J］．Math Oper Res，1982，7:211-222．

［5］ YAO J C．The generalized quasivariational inequality problem with applications ［J］．J Math Anal Appl，1991，158:139-160．

［6］ LALITHA C S，GUNEET BHATIA．Stability of parametric quasivariational inequality of the Minty Type ［J］．J Optim Theory Appl，2011，148(2):281-300．

［7］ KIEN B T，WONG N C，YAO J C．On the solution existence of generalized quasivariational inequalities with discontinue multifunctions ［J］．J Optim Theory Appl，2007，135(3):515-530．

［8］ AUBIN J P，EKELAND I．Applied nonlinear analysis［M］．Dover:Mineola，2006．

(责任编辑 马建华 英文审校 黄振坤)

Stability of Parametric Quasivariational Cone of the Minty Type

CHEN Jian-hong，HUANG Long-guang
(School of Science，Jimei University，Xiamen 361021，China)

Stability of a parametric quasivariational cone of the Minty type was studied in various sufficient conditions characterizing upper and lower semicontinuity of the solution sets as well as the approximate solution sets，which were similar to the solution sets of inequality．Sufficient conditions ensuring upper semicontinuity of the approximate solution sets of an optimization problem with quasivariational cone constraints were also presented．

quasivariational cone;stability;semicontinuity;closedness

O 174.13

A

1007－7405(2012)04－0301－04

2011－12－28

2012－03－21

国家自然科学基金资助项目 (11074099)

陈建弘 (1983—)，女，硕士生，从事应用泛函分析研究．通讯作者:黄龙光 (1961—)，男，教授，从事应用泛函分析研究，E-mail:hlgsj@163.com．