通过“一题多解”培养发散思维＊

蒋秀丽 李鹏飞 陈中华

（上海电力学院数理学院，上海 200090）

通过“一题多解”培养发散思维＊

蒋秀丽 李鹏飞 陈中华

（上海电力学院数理学院，上海 200090）

通过几道力学题目具体说明了“一题多解”在物理教学中的作用.“一题多解”有助于学生对课本知识深入理解；有助于培养学生的发散思维；有助于学生构建正确的物理图像.

一题多解；发散思维；物理图像

在物理的教学中，理论知识的传授是教学过程的中心环节，但要使学生能熟练地运用所学基本原理解决物理问题，仅靠课堂理论教学是远远不够的，精选并精讲一部分习题是必要的.但现在的教学中由于课时紧张等原因，教师在讲解题目时，往往只采用教材上的常规解法.虽然常规解法紧扣当堂课的知识点，针对性强，但结果使得很多学生在解答物理问题时，仅仅是单纯模仿教材或老师讲解的例题，简单地套用公式.作者在多年的教学中发现在习题讲解中采用“一题多解”的方式，对培养学生对问题的理解能力、对知识的应用能力有很好的效果.

所谓“一题多解”是指对同一个问题，沿着不同的方向去思考，从不同角度对所给信息加以重组，运用不同的概念、公式、原理来解题，而得到相同的结论.利用“一题多解”可以通过一个题目，学习掌握多个知识点，并达到融会贯通的效果，更重要的是，“一题多解”能训练学生思维的发散性和灵活性，提高解决问题的能力.本文通过几个力学题目的多种解法，说明“一题多解”的作用.

1 “一题多解”有助于培养学生的发散思维

例1 有人以v＝3m／s的速度向东奔跑，他感到风从北方吹来，当奔跑的速率加倍时，则感到风从东北方向吹来，求风的速度［1］.

图1 速度矢量图

解法1 图1中表示了人相对地的速度，风相对人的速度及风相对地的速度.如图所示，人以3m／s的速度奔跑时，人相对地的速度为v地人，风相对人的速度为v人风；人奔跑速度加倍后，人的速度为v′地人，此时风相对于人的速度为v′人风.由伽利略速度变换，风相对于地的速度为

由（1）、（2）两式可得

由矢量的加法可知，风相对地的矢量v地风为矢量v地人的起点指向矢量v人风终点，也是矢量v′地人起点指向矢量v′人风的终点.矢量v地人与v′地人起点相同，则v人风与v′人风应有相同的终点，即矢量v地风的终点.由图1的几何关系可知：即 风 速 为4.24m／s，方向为东偏南45°.

解法2 当人的速度为3m／s时，人相对地的速度、风相对人的速度、风相对地的速度如图2（a）所示，当人的速度为6m／s时，人相对地的速度、风相对人的速度、风相对地的速度如图2（b）所示.图中向右为东，θ为风向东偏南的角度.

图2 两种情况下的速度关系

由图2（a）可知

由图2（b）可知

由已知v地人＝3，v′地人＝6与方程（4）、（5）可得：v地风＝4.24m／s，θ＝45°.即风速为4.24m／s，方向为东偏南45°.

解法3 当人的速度为向东3m／s时，他感到风从北方吹来，则可知风相对地有向东3m／s的分量，故在东西方向人感觉不到风.当人的速度为向东6m／s时，风有向东3m／s的分量，则在东西方向人感到风向西3m／s；人感到风从东北方向吹来，则可知在南北方向人感到风向南也为3m／s，人在南北方向无分速度，则在南北方向，风相对地为向南3m／s.所以总体上风向为向东偏南45°，风速大小为

解法1的方法是通常教材中的解法.根据伽利略速度变换的知识，在人以不同速度奔跑的两种情况下，人相对地的速度与风相对人的速度相加是相等的，都是风相对地的速度.这是综合性较强的方法，在学生矢量知识运用还不熟练的情况下，有学生反映较难理解.解法2是将两种情况分离研究，从每种情况得到一定的信息，列出方程，求解方程组，再得到风对地的速度信息.解法3则运用了层层推理的方法，要求学生具有敏锐的分析能力.

“发散思维”是一种不依常规、寻求变异、从多角度多侧面思考问题，不拘泥于一种思考途径，不受现在知识的局限，也不受传统知识束缚的一种思维方式，是创新能力的一个重要元素.“一题多解”可以从全局综合的角度思考问题，也可以从细微之处找到几条线索，然后综合信息.“一题多解”能训练学生思维的发散性与灵活性，激发学生的创新思维.

2 “一题多解”有助于学生建立物理图像

例2 在地面以初速度大小v0，倾角θ，发射一物体（可视为质点），求物体的射程与射高.

解法1 以发射点为坐标原点，建立如图3所示坐标系.物体在水平方向为匀速运动，在竖直方向为竖直上抛运动.其运动方程为

图3 斜抛轨迹

解法2 以发射点为坐标原点，建立如图3所示坐标系.在竖直方向为竖直上抛运动.物体在竖直方向的速度为

在竖直方向的运动方程为

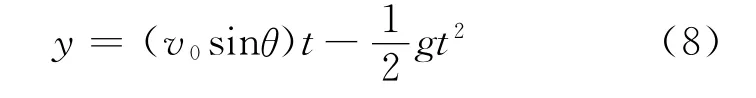
当物体到最高点时，竖直方向的速度为零，令式（7）中vy＝0，得t＝v0sinθ／g，代入式（8），得到，即射高.

在忽略阻力的情况下，当物体落地时，竖直方向的速度与上抛时竖直方向的速度大小相等，方向相反.vy＝－vy0＝－v0sinθ，代入式（7）得t＝2v0sinθ／g.物体在水平方向的运动方程为将落地时的时刻t＝2v0sinθ／g代入式（9），可得射程：

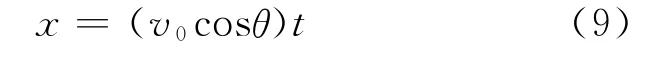
例3 一人从10m深的井中把10kg的水提上来，由于水桶漏水，每升高1m要漏去0.2kg的水.问要把水匀速地从水面提到井口，人做功多少［2］？

解法1 以水面为坐标原点，向上为x轴正方向.则水桶上升到x位置时，人的拉力为

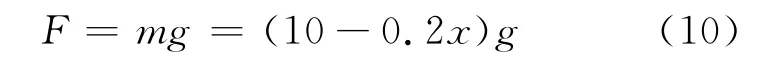
则把水桶提到井口，人做的功为

解法2 在水桶从水面到井口的过程中，共2kg的水逐渐漏出.剩余8kg的水被提至井口，人对此8kg的水做功A1＝m1gh＝8×9.8×10＝784（J）.对逐渐漏出的2kg的水，可视为一个高度为10m的水柱，其质心由井中水面升高至离水面5m处.则人对此2kg的水做功A2＝m2gh／2＝2×9.8×10／2＝98（J）.人共做功882J.

例2中的解法1，通过抛物线型的轨迹方程，用初等数学的知识求得射程与射高.这种解法物理意义体现不明显，且仅适用于轨迹为抛物线的情况.而解法2指出，在最高点，物体竖直方向的速度为零，物理意义非常清晰.通过这一物理现象，得到物体上升到最高点用的时间，进而求出物体射高.例3中的解法1是常规解法，根据变力做功的公式，用积分方法求解变力做功，可以很好地帮助学生掌握变力做功的计算方法.而解法2构想了一种等效的物理图像，将漏出的水等效为一个高10m的水柱.通过这种巧妙的构思，避免了变力做功中的积分运算，直观便捷地解决了问题.通过“一题多解”，可使学生明白建立物理图像的重要意义，锻炼建立恰当物理图像的能力.

3 总结

物理习题教学最基本的作用是巩固和深化所学的基本概念、基本理论及规律；更重要的目标是培养学生分析问题和解决问题能力，提高学生的创新思维能力.在习题讲解中采用“一题多解”的方法，通过不同的思维途径、从不同的方向、不同的侧面、不同的层次、运用不同的知识和方法解决同一问题，能有效地提高学生的思维能力.这样，使学生不仅能解题做题，更重要的是培养学生的理性思维能力，使他们具有运用物理知识解决实际问题的能力.

［1］ 程守洙，江之永.普通物理学（第六版）［M］.北京：高等教育出版社2006：26

［2］ 陈中华，阎明，宋青.大学物理学学习指导与能力训练［M］.上海：同济大学出版社，2008：45

2012-03-06）

上海市重点课程建设项目（20105306）.教育部高等学校物理基础课程教学指导分委员会高校教学研究项目（WJZW-2010-31-hd）.

蒋秀丽（1978年出生），女，博士在读，讲师，主要从事大学物理的教学.