货物配装和车辆路径问题的一种联合求解方法

孙 焰，张俊杰（同济大学 交通运输工程学院，上海 201804）

SUN Yan,ZHANG Jun-jie (School of Transportation Engineering,Tongji University,Shanghai 201804,China)

0 引 言

车辆路径问题 （VRP）是物流和相关领域的研究热点和难点，众多专家学者提出多种理论方法。这些求解方法主要分为两类：（1）精确求解算法：包括分支定界法、动态规划法、网络流算法、割平面法等； （2）（亚）启发式算法：遗传算法、蚁群算法等。精确算法不适用于求解大型VRP问题，遗传算法由于它模拟自然界 “物竞天择，适者生存”的进化机制，能很好地求解此问题。

通常，遗传算法求解VRP问题时分为两个阶段：首先确定需要安排配送任务的车辆数，再结合客户点数随机生成每个个体的染色体并进行遗传操作[1]。此类方法对于单车型且不考虑货物体积时适用，本文将探究考虑此两种因素时的解法设计，这也更符合实际情形。

1 问题提出

一个物流中心负责配送一块区域，现有多个订单分别配送到各客户点，请给出较合理配送方案，要求总成本最小。

已知：①客户点的收货时间窗、平均卸货速度 （kg/min）；②客户点之间的行程时间和费用；③配送中心有多种厢型 （长方体）车辆，最大载重和车厢内尺寸已知；④同一客户的多个订单组成一张临时订单，货物均认为是长方体包装，重量和尺寸均已知。

说明：①货物允许混装。②临时订单超出一辆车的重量或容积的装载能力时将分割成直送和配送两部分，配送部分不会超过任一类型的车辆的装载能力，本文仅考虑配送部分。③货物有三种装载要求：a.允许水平旋转，b.允许按任意坐标轴旋转，c.不可旋转。本文暂仅考虑a，较符合实际情况。

2 求解思路

要考虑货物的体积因素，就需要记录每个货物在车厢中的位置和码放方式，这正是典型货物配装问题。货物配装问题本身较复杂，三叉树算法是求解此问题的一种有效的启发式算法。为了结合使用遗传算法和三叉树算法，本文将会使用双层结构表示个体染色体，具体方法将在后文阐述。

3 货物配装问题

货物配装是NP完全问题，本文采用三叉树算法求解[2]，单个订单配装流程如下：首先将各订单的货物按体积递减排序，此后将按此顺序取货[3]；在初始空间 （空车厢）的左下角放入一定数量的货物 （若货物不能堆成长方体，将货物分成两部分，取能堆成长方体部分）后，空间被分隔成货物空间、边空间、前空间和上空间4个子空间。每次装货按照右、上、前的顺序遍历找出可用空间，然后装货。满足a.车辆的剩余载重不够装一件货物，b.车厢剩余空间都不够装一件货物，c.货物全部装完中任一配装结束。

装载完一个订单，检查车厢状态 （满足上文a或b或者c已装货物的重量或体积达到指定阀值，即认为已装满）。未装满时继续装下一个订单，若装满时最后一个订单未装完，撤消此订单的装载，选择下一辆空车装货。

显见，订单和车辆需要事先确定一个选取顺序。车辆本文暂按与所有订单的货物平均容重比C的接近程度从大到小排序[3],订单的排列顺序将取第4节的所述的染色体结构第一层序列。

4 车辆路径问题

车辆路径问题是一个NP困难问题，本文借鉴了染色体的双层结构表示方法[5]，并融入了一些新的想法，设计了满足求解本问题的并行遗传算法，现作详细介绍。

（1）客户点序号

从1开始给客户点 （即临时订单）编号，配送中心记为0；

（2） 染色体

双层结构表示：①865412739②0247，第一层是客户点序列，第二层是车辆序列。②的长度为4，表示需要四辆车，第一辆车从①的位置0开始，位置2前结束，即配送①的0,1两个位置点 （客户点8和6，装车顺序8、6，配送顺序6、8，二者顺序相反是因为先装后卸），以此类推，各车的配送客户分别为

程序在运行时，首先随机生成染色体第一层，然后据此利用第3节介绍的三叉树货物配装算法运算得到染色体第二层。随着第一层的客户点序列的不同，第二层序列的数字和长度也动态变化，这有别于传统方法需要事先确定所需车辆个数。

（3）种群初始化

设定种群规模N，选择概率Ps，交叉概率Pc，变异概率Pm。随机产生初始种群队列：对于每一个个体，首先产生染色体第一层，接着生成第二层车辆序列；计算配送方案的总费用，包括走行费用和惩罚成本；个体的适应度取总费用的倒数，适应度数值可适当放大。产生N个个体 （下标从0记起），个体按照适应度从大到小排序，记录最优个体。

（4） 选择

选择种群队列中前N*Ps个个体，作为下一代个体。

（5） 交叉

在种群队列的前Np=N*（1-Pc-P m）-1个个体中选择两个不同个体作为双亲，采用改进的顺序交叉 （允许双亲交叉长度不同）产生子代，从Np位置开始按顺序替换种群中个体。

（6） 变异

在种群队列的前Np个个体中随机选择一个作为父亲，从四种变异方法 （①交换变异，②反转变异，③插入变异，④子路径互换变异：交换两条子路径基因）中随机选择一种方法，变异产生子代。从Np+N*Pc开始按顺序替换种群中个体。

（7） 邻域搜索

取种群中第一个个体作为父亲，顺次采用 （6）的四种变异方法和⑤子路径交换变异⑥子路径反转变异⑦子路径插入变异三种方法产生子代。

需要设定邻域搜索的次数，每次搜索的结果都储存在第N-1位置个体中，并记录最优个体。

（8）2-opt路径优化

取种群中第一个个体作为父亲，对于染色体中的子路径 （需加入考虑配送中心），若图1中的ab+cd>ac+bd成立，则删除边ab和cd，连接ac和bd，并将b和c之间的客户点顺序反转。产生临时子代，记录最优个体。依次对各子路径 （长度大于2时）的边重复以上判断。

（9）重复步骤4,5,6,7,8,9

统计种群的代数和最优结果保持代数，满足结束条件时停止运行。

图2是遗传算法的算法流程：

图2 遗传算法流程图

图3是并行计算的详细设计：

对于父代种群和子代种群实际利用同一数组保存，遗传操作时种群个体按适应度排序，种群被分为适应度高和适应度低的两部分个体集合，即数组的前一部分保存适应度高的个体，剩下的部分保存适应度低的个体。算法步骤5,6,7,8中用来进行遗传操作的父代个体均来自适应度高个体集合，只进行读操作。复制其染色体，按顺序替换适应度低的个体，写操作发生在不同的适应度的个体上，相互没有影响。因而交叉、变异、邻域搜索和2-opt优化可以同时进行，即并行计算，可有效缩短运算时间，提高运行效率。

5 算例验证

物流中心的配送车辆技术参数见表1，将要配送货物的类型数据见表2，现有8辆空车等待分配运输任务见表3；表4是11张待送的临时订单数据。

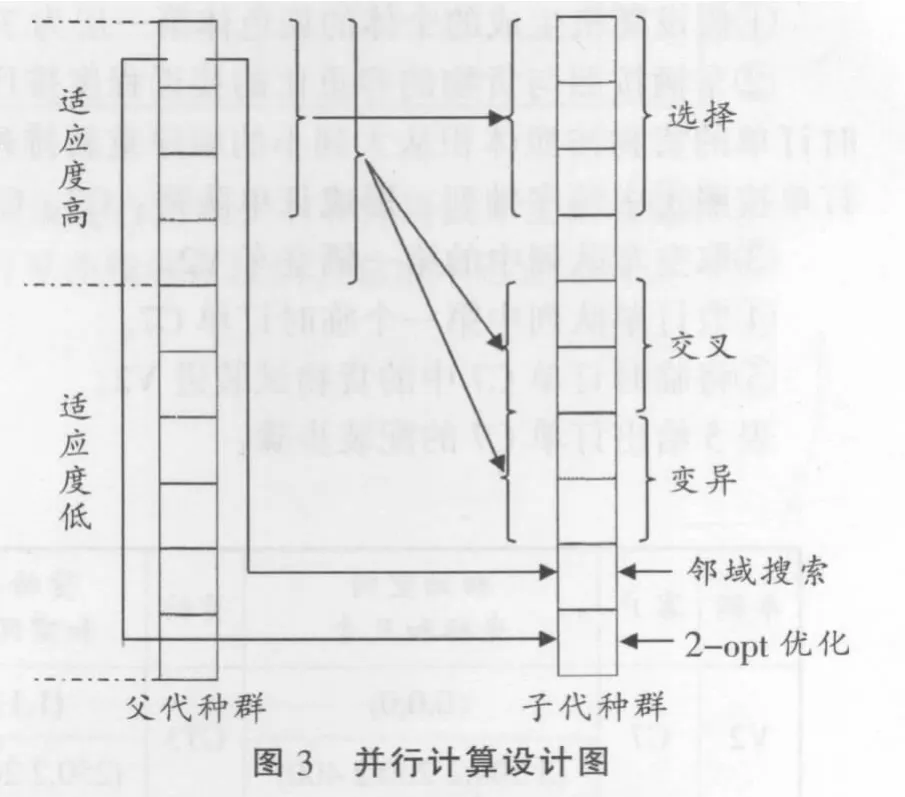
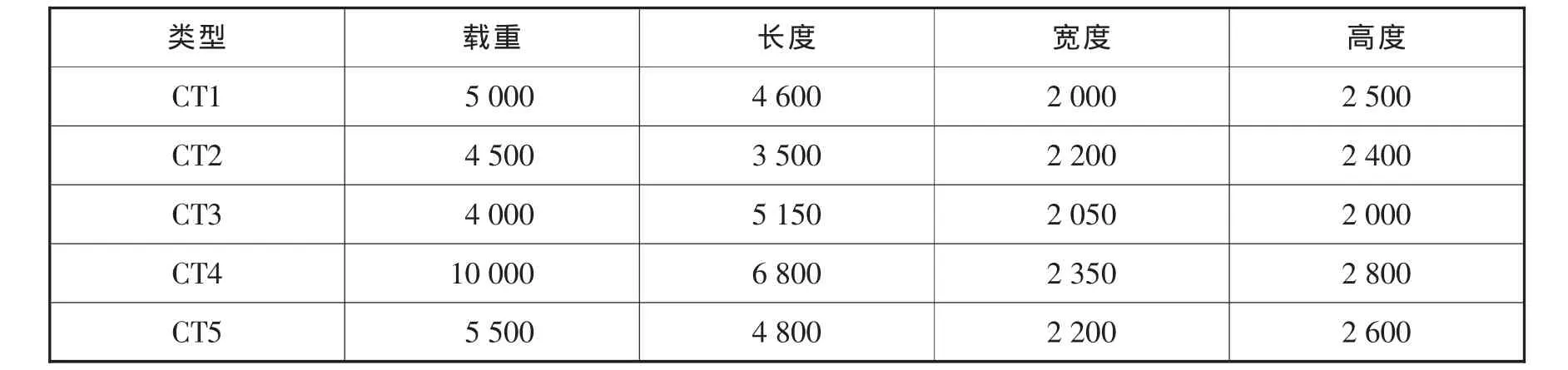
表1 车辆类型数据

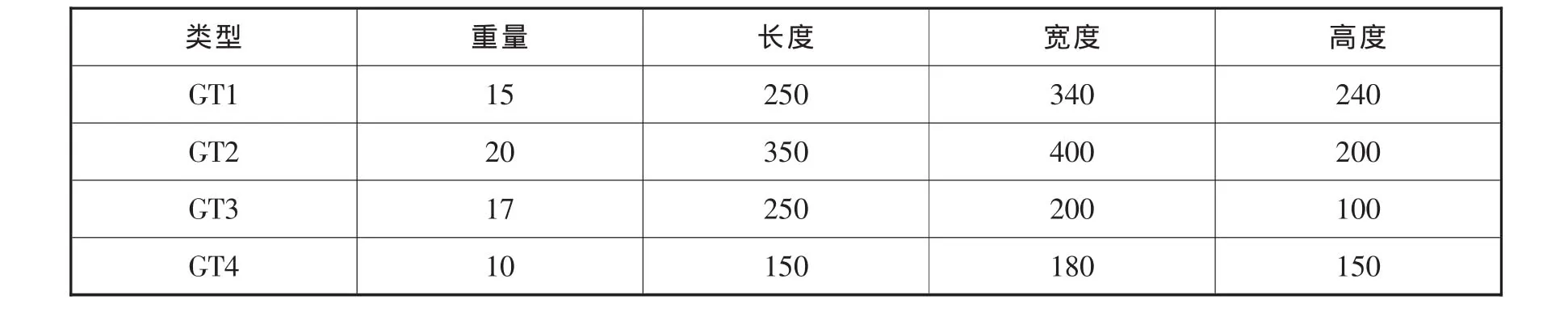
表2 货物类型数据

表3 现有空车数据

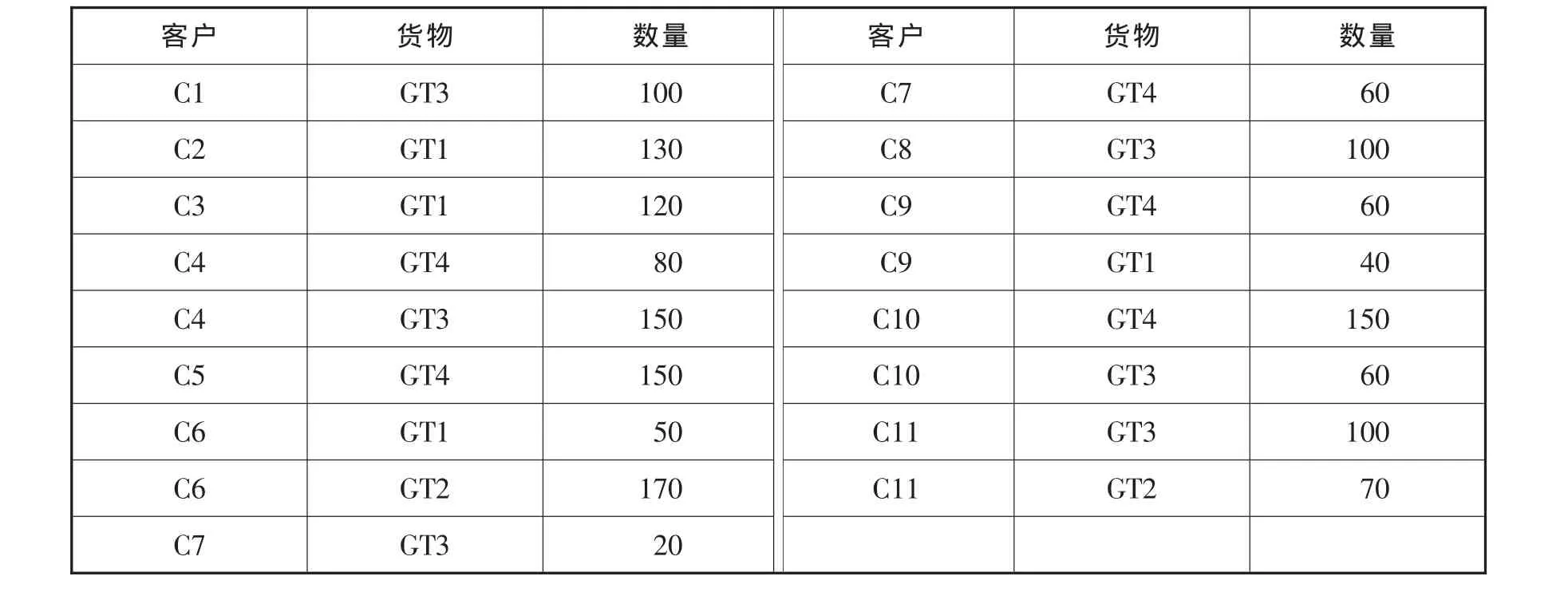
表4 临时订单数据

①假设随机生成的个体的染色体第一层为7、4、6、2、9、5、11、10、3、8、1。

②车辆按照与货物的容重比的接近程度排序，形成空车队列：V2、V7、V6、V4、V1、V8、V3、V5。每个临时订单的货物按照体积从大到小的顺序重新排列 （显然四种类型的货物体积顺序为GT2,GT1,GT3,GT4），将各临时订单按照①中顺序排列，形成订单队列：C7、C4、C6、C2、C9、C5、C11、C10、C3、C8、C1。

③取空车队列中的第一辆空车V2。

④取订单队列中第一个临时订单C7。

⑤将临时订单C7中的货物试装进V2。

表5给出订单C7的配装步骤：

表5 试装客户C7

此时车厢未满，取订单C4继续装货……

配装完毕，得到染色体的第二层序列为：0、2、3、7、9。

⑥计算个体的适应度，这需要以下数据：a.车辆离开物流中心的时间；b.每个客户点的收货时间窗数据和平均卸货速度；c.物流中心以及各客户点之间的路径费用和行程时间。如果已知数据中没有某两点之间的路径成本和行程时间数据，此路径被认为目前不能通过。可将路径成本设为0，行程时间设为1441min（大于一天）。

计算个体总成本需要以下数据：各点之间的路径成本和行程时间 （0是物流中心）数据，以及客户点的时间窗和平均卸货速度数据，篇幅关系不再列出。设定车辆离开物流中心的时间设为400，时间窗罚值为100 000，车辆的容积利用率和载重利用率达到80%以上认为车辆装满。得到总成本，取倒数，并放大1 000倍，得本例个体适应度为0.3155。

按照上面方法生成初始种群，设定Ps为0.3，Pc为0.5，Pm为0.1，最优个体保持代数为500，种群最大进化代数为3 000，其他遗传操作参见前文。经运算得到最优个体见表6：

根据最优个体的染色体得到配送清单，见表7：

表7中可以看出，共需要5辆车，第一辆车V2，货物的装车顺序为C3的120件GT1和C2的130件GT1（具体配装方案略），V2顺次配送客户C2和C3（非C3、C2）……

表6 最优个体

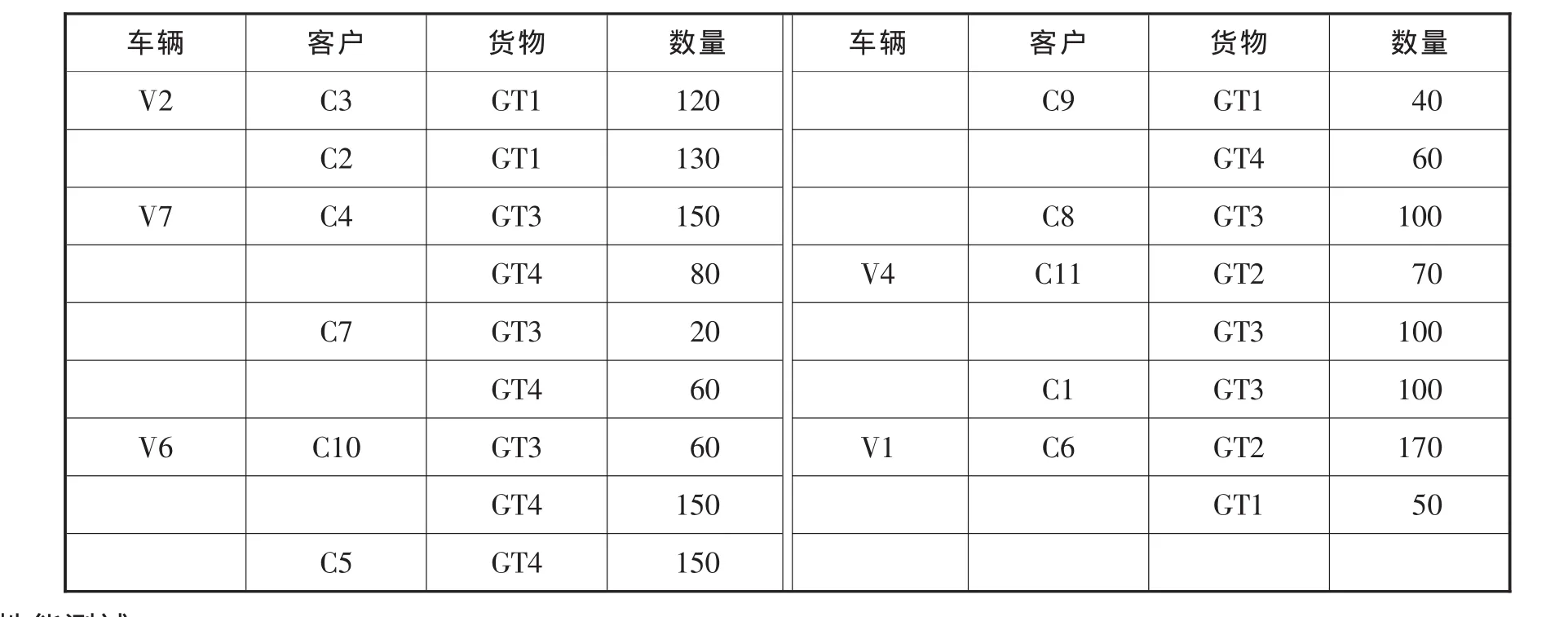
表7 配送清单

6 性能测试

本文在遗传算法中考虑了货物配装，不能采用Solomon基准测试集进行测试，本节将测试算法的收敛性。

图4是某次运算种群进化3 000代的最优个体的总成本曲线，可见曲线收敛较快，总成本迅速下降。

7 结束语

本文通过对车辆配装问题和车辆配送路径问题进行简明扼要的分析，始终从解决一个实际问题的角度出发，给出了一种联合求解此类问题的可行方法，经算例验证方法切实可行，算法收敛快。同时该方法还存在一些不足：如①邻域搜索在某个空间范围内增加了搜索深度，一方面能加快算法收敛，同时容易造成早熟；②算法中将车辆按照与货物平均容重比的接近程度排序，这样可以保证车厢空间尽可能得到利用，在单一车型的情况下可保证车辆数最少，在多车型情况下比较复杂，有待进一步论证。

总的来说，本算法对实际作业有一定的借鉴意义。

[1]孙焰.现代物流管理技术[M].上海：同济大学出版社，2004:153-158.

[2]姜义东，查建中，何大勇.集装箱装载矩形货物的布局研究[J].铁道学报：2000,22(6):13-18.

[3]刘霞，吕汉兴.集装箱装载矩形货物的一种启发式算法[J].起重运输机械，2003(1):16-18.

[4]孙焰，李致中.求双目标配装方案的多项式近似算法[J].长沙铁道学报，1997,15(2):33-39.

[5]姜昌华.遗传算法在物流系统优化中的应用研究[D].上海：华东师范大学 （博士学位论文），2006:81-103.