三层供应链协调运作的一个双向折扣模型

徐 鑫

（安徽大学 数学科学学院，合肥 230039）

三层供应链协调运作的一个双向折扣模型

徐 鑫

（安徽大学 数学科学学院，合肥 230039）

文章在前人研究的基础上，将需求看成是弹性的，并结合Khouja的多重折扣的研究，构建了一个三层供应链协调运作的双向折扣模型，即：既考虑销售商提供给客户一个折扣外，同时也将供货商提供给销售商的折扣纳入考虑之中；对于剩余产品的处理，将以一个低于成本的价格进行出售，针对上述情况构建使得总利润函数达到最大的数学建模，并通过模型求解得出双向折扣模型下的最优的初始订价和最优的折扣价格。最后给出一个算例对所构建模型进行了分析。

订购量；弹性需求；供应链；双向折扣

0 引言

当前市场销售易的产品，大多都是为了刺激顾客购买、降低自身的库存压力，提高自己懂得利润，所以在此目的下确定最优的订价策略和最优的折扣价格是一个值得研究的课题。目前，考虑采用价格折扣和数量折扣来协调供应链的相关文章很多，文献[1]提出一个临时性折扣下的最优经济订购批量的库存模型。文献[2]在不允许缺货的情况下，考虑总量折扣及超过部分才享有数量折扣的两种情况下最优经济批量的确定问题。文献[3]推导了具有多次折扣的报童问题，并说明了零售商若实行多次的折扣会比只使用单一的折扣得到比较高的期望利润。文献[4]建构了多项产品在储存及预算的双重限制下多次折扣的报童问题，并发展出一套算法来解决此问题。文献[5]针对单一周期的库存模型，在商品价格随季节变动时，以价格为基础建构库存模式，并进行相应参数的灵敏度分析。文献[6]探讨在线性需求函数且考虑多重折扣下之报童模式最佳化问题。

上述文献大从多数量折扣或价格折扣的角度对库存模型进行研究，但没有从买卖双方的联合成本方向对库存问题进行研究。

从文献的分析我们可以看出，在对供应链协调问题的研究中有些学者以价格折扣或数量折扣为主进行模型的建立和研究，也有些学者是从买卖双方的联合成本方向进行考虑构建库存协调模型，但我们发现同时考虑供货商与销售商一体化的库存文献却不多见。因此，本研究以此方向作为本文的研究主体，在给定订购量与初始订价的情形下，使用折扣价格及折扣数量为协调手段进行模型构建，并寻找最优的折扣次数和订购批量使得总利润达到最大化。

1 符号约定和假设

1.1 符号约定

P0：初始订价；

Pi：第i次的折扣价格(i=1,2)；

K：每次折扣的固定成本；

di：第i次折扣价格的区间(i=1,2,3)；

p：单位产品的成本价格；

Π：总利润函数；

P ：价格，它是需求的函数，即 P=α+βe-λx（λ为弹性系数）；

Xi：各价格点处的销售量(i=0,…,n)；

Xi,j：各价格点处的市场的销售量(j=0,…,n)；

Q：订购量；

I：成本回收比例系数（0＜I＜1）。

1.2 假设

（1）价格和需求的关系看成是弹性的；

（2）所销售的产品是没有变质的情况；

（3）初始订价由销售商依价格需求函数决定；

（4）每次的价格折扣都有固定成本的支出。

2 模型建立及求解

2.1 销售商在销售过程中针对下游顾客的折扣模型及求解

由图1发现，销售商销售该商品的初始订价为P0，若销售数量达到 X0=λ-1[lnβ-ln(a+d1+d2+d3)]，则进行第一次折扣，第一次折扣订价为P1；若销售数量达到X1=λ-1⋅[lnβ-ln(a+d2+d3)]，则进行第二次折扣，第二次折扣定价为 P2；并于最后将数量 X2=λ-1[lnβln(a+d3)]全部售完。

图1 销售商价格需求函数

因此，如何决定初始订价P0、第一次折扣价格P1以及第二次折扣价格P2是使得总利润达到最大化的关键所在；而确定P0、P1以及P2的实质在于确定出每次折扣的折扣区间值，即d1、d2和d3。总利润函数由上述假设和条件可知为如下形式，即：

为了使得总利润达到最大，也就是是使得（1）式的结果达到最大，即：

由式(8)可知，β为d3的函数，因此求解最优的d3值时，可运用如下的数值分析算法进行求解。

（1）设定各项参数之初值。

（2）建立数学表达式

（3）设d3=0为起始值，代入公式(9)，求得 f(d3)值。

（4）令 d3=d3+ Δ x ，代入公式(9)，计算 f(d3)值，若f(d3)＞0，则重复执行该步骤。

（5）若 f(d3)＜0，则执行步骤（6）。

（7）显示最终结果 d3=d3－ Δ x ，将 d3代入式(6)、(7)得到d1、d2值并结束。

在给定β下，求解符合要求之近似解d3，再代回公式(6)、公式(7)得到 d1、d2。

定理Π(d1,d2,d3)为严格凹函数，且在d1、d2、d3处取得极大值（证明略） 。

2.2 销售商针对上游供应商供货过程中的折扣模型及求解

上游供货商对销售商所提供的折扣为如图2所示。

图2 销售商针对供应商提供的进货折扣

依据销售商所制定的折扣价格以及不同的订购量所导致的购买单价不同，我们可以得到不同进货成本下的总利润函数为：

其中I（0＜I＜1）值为成本回收比例系数，其涵义为：剩余部份以低于成本价销售。

为求得使得总利润达到最大的最大值和最优订购批量，其求解过程如下：

（1）计算各个折扣成本下之最优订购量X2,j；

（2）找出折扣最大、且为折扣范围内的最优订购批量：

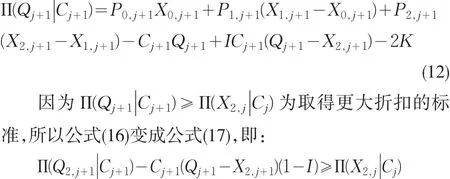
同理当折扣大于Cj+1，可针对各个折扣成本做探讨，则公式(14)可以一般式表示之，如公式(14)所示。

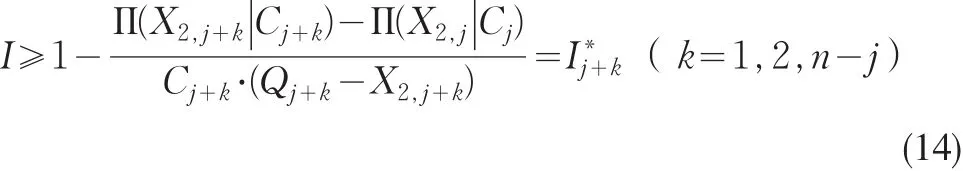
因此，在0＜I＜1的条件下，我们可知：

（1）若I≥Ij∗+1，则需要取得更大的折扣，接着只需比较下一个边界点之后的总利润值 Max{Π(Qj+k|Cj+k),k=1,2,...,n-j}即可发现总利润最大值。

3 算例

表1 相关参数值

根据表1和图3由(9)式运用Matlab软件求解最优d3值为 d3=59；代入(6)式、(7)式，得 d2=76、d1=94。

可知总利润为Π(59,76,94)=10668.56。

另外得知初始订价 P0=469，若销售数量达到X0=33，则进行第一次折扣，第一次折扣订价P1=375，若销售数量达到X1=71.7，则进行第二次折扣，第二次折扣订价 P2=299 。 X2=λ-1⋅[lnPd-ln(a+d3)]=121.2 为最优订购量，此时总利润10668.56元为最大值。

依据上述方法求得各进货成本下之总利润、最优订购批量与临界订购批量并结合所选的0＜I＜1的值加以分析，见表2。

表2 在0＜I＜1情况下不同折扣所对应的最优解

若I≥0.66，要取得更大的折扣，则可获得总利润最大值；若I＜0.66，不需要取得更大的折扣。

4 结论

本文研究以Khouja的文章为参考依据，将价格需求函数改为弹性性模型，进行具双向折扣之最优订购量及最优订价策略分析，并给出了相应的算例分析。本文考虑三个价格，后续研究可针对更多重之折扣问题加以分析。可以将进货折扣过程中的折扣点的设计考虑成决策变量进行进一步的模型构建。

[1]Tersine,R.J.，R.L.Price,Temporary Price Discd Materials Manage⁃ment[J].Journal of Purchasing Production and Inventory Management,1981（,15）.

[2]Tersine,R.J.，R.A.Toelle.Lot Size Determination with Quantity Dis⁃counts[J].Production and Inventory Management,1985,26（3）.

[3]Khouja,M.The Newsboy Problem under Progressive Multiple Dis⁃counts[J].European Journal of Operational Research,1995,84（2）.

[4]Khouja,M.，A.Mehrez.A Multi-Product Constrainted Newsboy Prob⁃lem with Progressive Multiple Discounts[J].Computers Industrial Engi⁃neering,1996,30（1）.

[5]Urban,T.L.，R.C.Baker.Optimal Ordering and Pricing Policies in a Single-period Environment with Multivariate Demand and Markdowns[J].European Journal of Operational Research,1997,(103).

[6]Khouja,M.Optimal Ordering,Discounting,and Pricing in the Sin⁃gle-period Problem[J].International Journal of Production Economics,2000,(65).

F270.5

A

1002-6487（2012）24-0057-03

国家自然科学基金资助项目(70571001)；安徽省优秀青年科技资助项目(08040106835)；安徽省教育厅资助项目(KJ2011Z018)；安徽省自然科学基金资助项目(070416245)

徐 鑫（1979-），男，安徽巢湖人，硕士，讲师，研究方向：运筹与决策、方程和控制理论。

（责任编辑/亦 民）