供应链条件下制造业寄售库存合作伙伴选择研究
2012-10-20肖建华任顺霞
肖建华,任顺霞,秦 凡
(南开大学a.现代物流研究中心;b.物流管理系,天津 300071)
0 引言
随着全球化经济的快速发展,传统的企业经营方式已经越来越不适应新时代竞争的要求,供应链管理(SCM)应运而生,而作为供应链管理的核心内容——库存管理,已成为学者的研究热点和难点。寄售库存(CS)作为一种新兴的、先进的库存管理模式和以“零库存”为目标的库存成本控制方法,在供应链管理中正在发挥着其独有的作用,引起了人们越来越多的重视。
在制造型企业中,由于存在生产报废、客户订单量不稳定、生产返工、来料检验不合格退货等不确定性因素,越来越多的企业开始采用寄售库存模式。然而,制造企业要实现寄售库存,首要的问题是合作伙伴选择。目前,有关供应链合作伙伴选择的研究相对比较成熟,研究文献主要集中在供应链合作伙伴评价指标体系的构建和方法选择等方面[1~4]。而寄售库存模式下的合作伙伴选择研究目前还鲜有研究。因此,本文试图构建供应链条件下寄售库存合作伙伴的评价指标体系,将定量与定性研究相结合,提出基于AHP-DEA的两阶段寄售库存合作伙伴选择模型,应用于求解寄售库存模式下的制造企业合作伙伴的选择问题。
1 制造业寄售库存合作伙伴评价指标体系设计
本文在借鉴传统供应链合作伙伴选择指标体系的基础上,结合寄售库存模式的基本特性,遵循双赢性、实效性、全面性、简洁性等原则,主要从产品、服务和企业实力三个方面构建寄售库存模式下合作伙伴选择评价指标体系,如表1所示。

表1 制造业寄售库存合作伙伴选择评价指标体系
制造业寄售库存合作伙伴选择评价指标体系可以看作一个投入产出系统,其评价指标的属性可分为负向指标(越小越好型)和正向指标(越大越好型)两大类。显然,产品价格、响应速度和管理状况三个指标作为负向指标,即投入指标;产品质量、产品重要程度、合作意愿与经验、物流水平、生产能力及盈利状况六个指标作为正向指标,即产出指标。
此外,本文中的产品质量、产品价格、产品重要程度、物流水平、响应速度、生产能力为定量指标,而合作意愿与经验、盈利状况及管理状况为定性指标,需应用AHP法将其定量化。
2 供应链条件下制造业寄售库存合作伙伴评价模型
本文提出了一种将AHP和DEA相结合的寄售库存合作伙伴选择评价模型。即利用AHP确定制造企业寄售库存的评价指标体系的一二级指标权重,并通过模糊综合评价法(Fuzzy Comprehensive Evaluation Method,FCEM)对指标评价体系进行合理性验证;然后把权重数据输入到DEA模型选择合作伙伴。
2.1 利用AHP法确定评价指标权重
(1)建立层次结构模型
通过第二节的系统分析,综合考虑寄售库存环境下制造型企业供应商选择的定性和定量影响因素,把供应商总体综合水平作为供应商伙伴选择的目标层,将产品层面、服务层面和企业实力层面以及相面的评价指标作为准则层来构造层次结构模型。
(2)构造比较判断矩阵,计算权重
专家依据相对重要性的判断,对某上层准则Ck下的n个同级指标P1,P2,…,Pn进行两两比较,构造比较判断矩阵Bk,即:

其中,bij代表评价指标Pi相对于评价指标Pj的重要程度;bji=1/bji,若i=j,则bij=1。
通过公式BkW=λmaxW,求解出所对应的特征向量W。其中,W经归一化后,即为各相应评价指标的权重。
(3)矩阵一致性判断
计算一致性指标CI和随机一致性比率CR,公式如下:

其中,λmax为判断比较矩阵的最大特征根,RI为平均随机一致性指标,可以通过查表法得到。若CR≤0.1时,则具有满意的一致性;反之,则需修正判断矩阵的数值,以满足一致性检验。
通过上述建立的层次分析模型,寄售库存指标体系各层指标权重及总排序如表2所示。
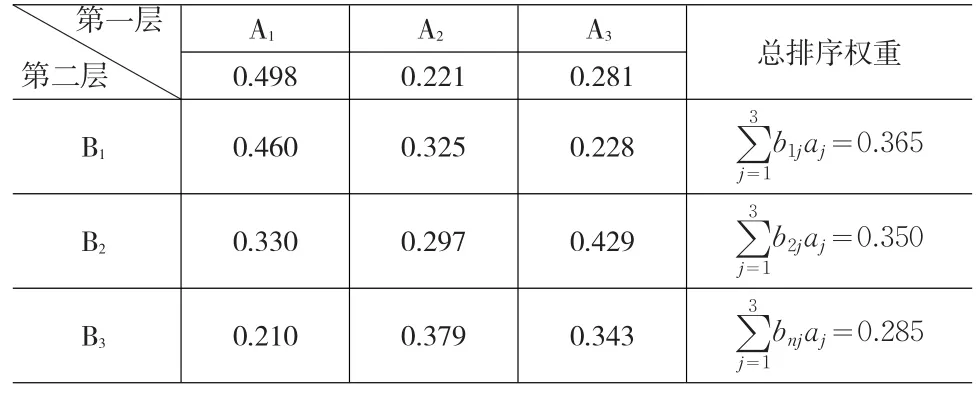
表2 寄售库存指标评价体系各层指标权重及排序
2.2 利用FCEM法验证评价指标体系的合理性
为避免主观性太强,在层次分析法的基础上,通过模糊综合评价法对评价指标的合理性进行检验。模糊综合评价法的关键在于构造隶属评价矩阵,即求解从指标集U={U1,U2,…,Ui,…,Un}到评价集V={V1,V2,…,Vj,…,Vm}的模糊映射。单因素评价矩阵可定义如下:

其中,rij为评价指标Ui获得评价Vj的隶属关系,即:

其中:vij表示评价指标Ui获得评价等级Vj的个数。
则模糊综合评价模型为:
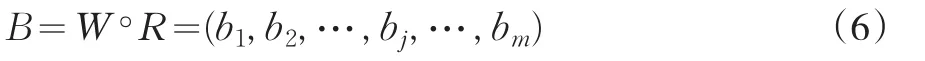
式中“∘”为广义模糊算子,W为指标权重向量。当进行综合评价时,可得出加权平均型算子,即:

根据B′的计算结果,检验指标体系是否合理。
本文采用了专家打分法来进行合作伙伴指标体系的评价,共发放问卷50份,回收47份,回收率为94%。参与问卷调查的对象均为采购经理、采购工程师或者其他长期工作在制造业具有丰富物流经验的人员,其问卷调查所得结果如表3所示。

表3 制造业寄售库存伙伴选择指标体系合理性调查数据
根据以上内容及对专家的问卷调查结果,可以对指标体系的合理性进行评价。首先,根据问卷调查结果,建立单因素评价矩阵。其中,供应商能力水平单因素评价矩阵R1为:

由上节内容可知,权重向量w1=(0.460 0.330 0.21),则模糊综合评价为:

因此,34.2%的专家认为产品层面对供应商能力评价影响很大;39.8%的专家认为产品层面对供应商能力评价影响较大;20.7%的专家认为产品层面对供应商能力评价影响一般。可以看出,产品层下的各评价指标基本合理。同理,服务层面和企业实力两层下的评价指标选择合理。
2.3 利用DEA模型计算相对有效性
为利用数据包络分析法进行评价,将每个被评价对象作为一个决策单元(DMU),被评价群体由众多DMU组成。设有n个DMU,每个DMU有m个输入及s个输出。其中,DMUj的输入向量为Xj=(x1j,x2j,…,xmj)T和输出向量为Yj=(y1j,y2j,…,ysj)T。 xij为第 j个DMU的第i种类型的输入值,xij>0;yrk为第r个DMU的第k种类型的输出量,yrk>0。则可以构造对于第 j个决策单元的DEA投入和产出BCC线性规划模型为:

其中,Xj为第 j个输入指标向量;Yj为第 j个输出指标向量;E为投入缩小比率;ωj为决策单元线型组合的系数。
通过式(9),求解出各候选合作伙伴的效率值。若E等于1,则该决策单元DEA有效。
3 实例分析
DF公司是丹麦最大的生产制造型企业,在我国天津设有工厂,2008年经济危机以来,亟需采取进口原材料本地化来降低公司成本。考虑运输时间短、售后服务方便等因素,公司倾向于从京津冀地区选择供应商,且基于降低库存成本的要求,供应商供货须采用寄售库存模式。采购人员根据合作经验和市场调查,通过专家初步筛选出符合要求的6家候选合作伙伴:H1,H2,H3,H4,H5和H6。
根据第2节确定的评价指标体系,共有3个定性评价指标,即合作意愿与经验、盈利状况及管理状况。在应用DEA模型进行有关投入与产出评价之前,需将这3个指标用AHP法进行量化,得到相对权重。采购人员根据合作经验和市场调查结果,对6个候选伙伴进行对比评估,结果如表4至表6所示。

表4 合作意愿与经验判断矩阵
计算CI=0.108,查表得RI=1.25,则CR=0.087<0.1,通过一致性检验。

表5 盈利状况判断矩阵
CI=0.096,n=6,查表得RI=1.25,CR=0.077<0.1,通过一致性检验。
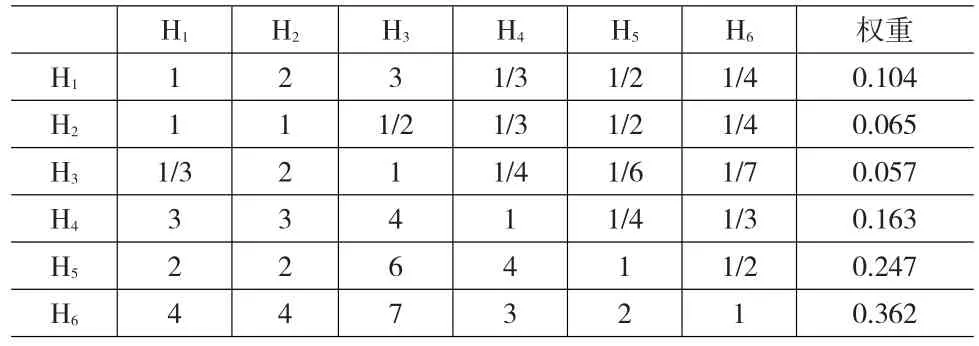
表6 管理状况判断矩阵
CI=0.117,n=6,查表得RI=1.25,CR=0.094<0.1,通过一致性检验。
通过以上三个比较判断矩阵,合作意愿与经验、盈利状况和管理状况这3个定性指标各自的权重得以量化,其结果将用于合作伙伴的DEA评价中。

表7 候选合作伙伴的输入和输出
通过对候选伙伴的调查了解,结合层次分析法得到的量化指标,得到候选伙伴的输入和输出,如表7所示。
利用BCC模型,求得候选伙伴效率,结果如表8所示。

表8 DEA模型求解结果
从上述计算结果可以看出,候选合作伙伴H4和H5的综合指数能力最低,不考虑作为DF公司的供应商,而H1和H3的综合指数最高,可以作为公司底板件的供应商。但H2和H6还存在改善空间,如两个公司在自己较弱方面能够进行改善,还有可能成为具有竞争力的供应商。其中,H2的弱项在于合作意愿与经验不足和管理状况较差。如合作意愿不足,则说明H2公司主观上对该合作兴趣不高,无须考虑该供应商;而H6的合作意愿与经验均好于H2,但生产能力存在严重问题,若该公司能够通过购买新的设备或者招聘更多的员工来解决生产能力问题,H2还可以发展为DF公司的供应商。
4 结束语
本文构建了供应链条件下制造业寄售库存合作伙伴的评价指标体系,并利用模糊综合评价法对指标评价体系的合理性进行了验证。在此基础上,提出了基于AHP-DEA的寄售库存合作伙伴选择模型,以用于对寄售库存条件下的合作伙伴的选择。本文还以DF公司寄售库存环境下底板件供应商选择为例,说明了此合作伙伴选择模型的有效性和可行性。
[1]Wu C,Barnes D.Formulating Partner Selection Criteria for Agile Sup⁃ply Chains:A Dempster-Shafer Belief Acceptability Optimisation Ap⁃proach[J].International Journal of Production Economics,2010,125(2).
[2]J F Yue,Yu Xia,T Tran.Selecting Sourcing Partners for A Make-to-order Supply Chain[J].Omega,2010,38(3~4).
[3]Yeh W C,Chuang M C.Using Multi-Objective Genetic Algorithm for Partner Selection in Green Supply Chain Problems[J].Expert Systems with Applications,2011,38(4).
